Kezdőlap


Cím:	Az 54. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Füzet:	2013/október, 386 - 395. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

\begin{matrix} A szerkesztőség \end{matrix}

1. Bizonyítsuk be, hogy bármilyen pozitív egész

k

és

n

számok esetén található

k

(nem feltétlenül különböző) pozitív egész:

m_{1}, m_{2}, ..., m_{k}

, amikre

\begin{matrix} 1 + \frac{2^{k} - 1}{n} = (1 + \frac{1}{m_{1}}) (1 + \frac{1}{m_{2}}) \dots (1 + \frac{1}{m_{k}}) . \end{matrix}

Havasi Márton megoldása.¹ Az állítást

k

-ra vonatkoztatott indukcióval bizonyítjuk. A következőt fogjuk belátni:

k = 1

-re, az

m_{1} = n

triviálisan megoldás.
Feltesszük, hogy az állítás igaz egy pozitív egész

k

-ra. Azt akarjuk belátni, hogy minden

n

egészhez léteznek

m_{1}, ..., m_{k + 1}

egészek, amelyek kielégítik az

\begin{matrix} 1 + \frac{2^{k + 1} - 1}{n} = (1 + \frac{1}{m_{1}}) \dots (1 + \frac{1}{m_{k + 1}}) \end{matrix}

egyenletet. Két esetet különböztetünk meg

n

paritásától függően.
1. eset:

n

páratlan. Ekkor

\frac{n + 1}{2}

biztosan egész és a feltételből adódóan léteznek olyan

m_{1}, ..., m_{k}

egészek, amelyekre teljesül

\begin{matrix} 1 + \frac{2^{k} - 1}{\frac{n + 1}{2}} = (1 + \frac{1}{m_{1}}) \dots (1 + \frac{1}{m_{k}}) . \end{matrix}

Legyen

m_{k + 1} = n

. Ekkor:

\begin{matrix} (1 + \frac{1}{m_{1}}) \dots (1 + \frac{1}{m_{k + 1}}) = (1 + \frac{2^{k} - 1}{\frac{n + 1}{2}}) \cdot (1 + \frac{1}{n}) = \\ = (1 + \frac{2^{k + 1} - 2}{n + 1}) \cdot \frac{n + 1}{n} = \frac{n + 1 + 2^{k + 1} - 2}{n} = 1 + \frac{2^{k + 1} - 1}{n} . \end{matrix}

2. eset:

n

páros. Ekkor

\frac{n}{2}

biztosan egész és a feltételből adódóan léteznek olyan

m_{1}, ..., m_{k}

egészek, amelyekre teljesül

\begin{matrix} 1 + \frac{2^{k} - 1}{\frac{n}{2}} = (1 + \frac{1}{m_{1}}) \dots (1 + \frac{1}{m_{k}}) . \end{matrix}

Legyen

m_{k + 1} = 2^{k + 1} + n - 2

. Ekkor:

\begin{matrix} (1 + \frac{1}{m_{1}}) \dots (1 + \frac{1}{m_{k + 1}}) = (1 + \frac{2^{k} - 1}{\frac{n}{2}}) \cdot (1 + \frac{1}{2^{k + 1} + n - 2}) = \\ = (1 + \frac{2^{k + 1} - 2}{n}) \cdot (1 + \frac{1}{2^{k + 1} + n - 2}) = \frac{2^{k + 1} + n - 2}{n} \cdot \frac{2^{k + 1} + n - 2 + 1}{2^{k + 1} + n - 2} = \\ = 1 + \frac{2^{k + 1} - 1}{n} . \end{matrix}

2. A sík

4027

pontjából álló alakzatot kolumbiainak nevezzük, ha

2013

pontja pirosra, a többi

2014

kékre van színezve, és az alakzat semelyik három pontja sincs egy egyenesen. Néhány egyenese meghúzásával a síkot tartományokra bontjuk. Az egyeneseknek ezt az elrendezését a kolumbiai alakzatra nézve jónak nevezzük, ha a következő két feltétel teljesül:

$•$	semelyik egyenes sem megy át az alakzat semelyik pontján sem;

$•$	nincs olyan tartomány, amelyik mindkét színű pontot tartalmaz.

Határozzuk meg a legkisebb olyan

k

értéket, amire igaz az, hogy

4027

pontból álló bármely kolumbiai alakzatra van

k

egyenesből álló jó elrendezés.

Tardos Jakab megoldása. A legkisebb megfelelő

k

a 2013. Nem lehet 2013-nál kisebb, mivel létezik olyan kolumbiai alakzat, amelyet nem lehet 2013-nál kevesebb egyenessel jól felbontani.
Vegyünk egy szabályos 4027-szöget. A sokszög csúcsait színezzük felváltva kékre és pirosra úgy, hogy egy helyen két szomszédos csúcs kék színű legyen. Ekkor a 4027-szög csúcsai egy kolumbiai alakzatot alkotnak. A 4027-szögnek pontosan 4026 olyan oldala van, amelyeket egy piros és egy kék pont határol. Ha ezt az alakzatot egyenesekkel jól felbontjuk, minden ilyen oldalt el kell metszenie legalább egy egyenesnek. Ha a 4026 oldal közül lenne egy, amelyet egy egyenes sem metsz el, akkor az ezt határoló két különböző színű csúcs egy tartományba esne. Mivel a szabályos 4027-szög konvex alakzat, minden egyenes legfeljebb kétszer metszheti; ahhoz, hogy 4026 helyen el legyen metszve, legalább 2013 egyenes kell.
Igaz, hogy 2013 egyenes minden kolumbiai alakzat jó felbontásához elég.
Lemma. Bármely két pontot el lehet választani az alakzat többi pontjától két egyenes felhasználásával. Legyen a két pont

A

és

B

. Legyen az

A B

egyeneshez legközelebbi pont (

A

-n és

B

-n kívül)

C

. Ha

C

és

A B

távolsága

x

(ahol

x

pozitív, mivel az

A B

egyenes nem tartalmazhat harmadik pontot), akkor a két

A B

-vel párhuzamos, tőle

x / 2

távolságra lévő egyenest behúzva valóban elválasztottuk

A

-t és

B

-t az alakzat többi pontjáról.
Ha egy kolumbiai alakzat konvex burka tartalmaz piros pontot, a következőképpen lehet 2013 egyenessel jól felbontani:
A konvex burokban lévő piros pontot elválasztjuk az alakzat többi pontjától egy egyenessel. A maradék 2012 piros pontot 1006 párba állítjuk, majd a párokat elválasztjuk az alakzat többi pontjától, a lemma szerint, 2012 egyenes felhasználásával. Így egy 2013 egyenesből álló jó felbontást alkottunk.
Ha egy kolumbiai alakzat konvex burka nem tartalmaz piros pontot, a következőképpen lehet 2013 egyenessel jól felbontani:
A konvex burok két szomszédos kék pontját egy egyenessel leválaszthatjuk. A maradék 2012 kék pontot 1006 párba állítjuk, majd a párokat elválasztjuk az alakzat többi pontjától, a lemma szerint, 2012 egyenessel. Így ismét egy 2013 egyenesből álló jó felbontást alkottunk, tehát minden kolumbiai alakzatot jól fel lehet bontani 2013 egyenessel.
A legkisebb megfelelő tulajdonságú

k

valóban a 2013.

3. Az

A B C

háromszög

A

csúccsal szemközti hozzáírt köre érintse a

B C

oldalt az

A_{1}

pontban. Hasonlóan definiáljuk a

C A

oldal

B_{1}

pontját, ill. az

A B

oldal

C_{1}

pontját a

B

-vel, ill.

C

-vel szemközti hozzáírt körök segítségével. Tegyük fel, hogy az

A_{1} B_{1} C_{1}

háromszög körülírt körének a középpontja az

A B C

háromszög körülírt körén fekszik. Bizonyítsuk be, hogy az

A B C

háromszög derékszögű.
Az

A B C

háromszög

A

csúccsal szemközti hozzáírt köre az a kör, ami érinti a

B C

szakaszt, továbbá az

A B

félegyenes

B

-n túli részét és az

A C

félegyenes

C

-n túli részét. Hasonlóan vannak definiálva a

B

, ill. a

C

csúccsal szemközti hozzáírt körök.

Szabó Attila megoldása. Az általánosság megszorítása nélkül feltehetjük, hogy az

A_{1} B_{1} C_{1}

kör

P

középpontja a körülírt kör

B

-t nem tartalmazó

A C

ívén van. A háromszög oldalait és szögeit a szokásos módon jelöljük, félkerülete

s

, területe

t

, beírt és körülírt körének sugara rendre

ϱ

és

R

. Legyenek a

P A

P B

P C

szakaszok látószögei rendre

P B A ∢ = P C A ∢ = α'

P C B ∢ = π - P A B ∢ = β'

és

P A C ∢ = P B C ∢ = γ'

. Ekkor a szinusztétel miatt

\begin{matrix} P A = 2 R sin α', P B = 2 R sin β', P C = 2 R sin γ', \end{matrix}

(1)

a következő összefüggések egyszerű szögszámolással adódnak:

\begin{matrix} π - β' = α + γ', β = α' + γ', β' = γ + α' . \end{matrix}

(2)

Ismert továbbá, hogy

C B_{1} = B C_{1} = s - a

A C_{1} = C A_{1} = s - b

A B_{1} = B A_{1} = s - c

.
Írjuk fel a koszinusztételt a

B_{1} C P

és

C_{1} B P

háromszögekben:

\begin{matrix} P B_{1}^{2} & = {(s - a)}^{2} + C P^{2} - 2 (s - a) C P cos α'; & (3) \\ P C_{1}^{2} & = {(s - a)}^{2} + B P^{2} - 2 (s - a) B P cos α' . & (4) \end{matrix}

Mivel

P B_{1} = P C_{1}

, a két jobb oldal egyenlő:

\begin{matrix} C P^{2} - 2 (s - a) C P cos α' = B P^{2} - 2 (s - a) B P cos α', \\ (C P - B P) (C P + B P) = C P^{2} - B P^{2} = 2 (s - a) (C P - B P) cos α' . & (5) \end{matrix}

B_{1} A P

és

A_{1} B P

háromszögekben felírt koszinusztételekből ugyanígy következik, hogy

\begin{matrix} (A P - B P) (A P + B P) = 2 (s - c) (A P - B P) cos γ' . \end{matrix}

(6)

Az (5), (6) egyenletek

C P = B P

, illetve

A P = B P

esetén is teljesülnek. Ha viszont mindkettő teljesülne,

P

A B C

kör középpontja lenne, ami ellentmondás: az általánosság megszorítása nélkül feltehető, hogy

C P \neq B P

. Ekkor (5) mindkét oldalát eloszthatjuk

(C P - B P)

-vel:

\begin{matrix} C P + B P = 2 (s - a) cos α', & (7) \\ 2 R (sin γ' + sin β') = (b + c - a) cos α' = 2 R (sin β + sin γ - sin α) cos α', \\ sin (β - α') + sin (γ + α') = (sin β + sin γ - sin α) cos α', \\ sin β cos α' - cos β sin α' + sin γ cos α' + cos γ sin α' = \\ = sin β cos α' + sin γ cos α' - sin α cos α', \\ sin α cos α' = sin α' (cos β - cos γ), \\ ctg α' = \frac{cos β - cos γ}{sin α} . & (8) \end{matrix}

Most írjuk fel a koszinusztételt az

A_{1} C P

és

A C_{1} P

háromszögekben is:

\begin{matrix} P A_{1}^{2} & = {(s - b)}^{2} + P C^{2} - 2 (s - b) P C cos β'; & (9) \\ P C_{1}^{2} & = {(s - b)}^{2} + P A^{2} + 2 (s - b) P A cos β' . & (10) \end{matrix}

P A_{1} = P C_{1}

miatt a két jobb oldal egyenlő:

\begin{matrix} P C^{2} - 2 (s - b) P C cos β' = P A^{2} + 2 (s - b) P A cos β', & (11) \\ (P C - P A) (P C + P A) = P C^{2} - P A^{2} = 2 (s - b) (P A + P C) cos β', \\ P C - P A = 2 (s - b) cos β', \\ 2 R (sin γ' - sin α') = (a + c - b) cos β' = 2 R (sin α + sin γ - sin β) cos β', \\ sin (β' + α) - sin (β' - γ) = (sin α + sin γ - sin β) cos β', \\ sin β' cos α + cos β' sin α - sin β' cos γ + cos β' sin γ = \\ = sin α cos β' + sin γ cos β' - sin β cos β', \\ sin β' (cos γ - cos α) = sin β cos β', \\ ctg β' = \frac{cos γ - cos α}{sin β} . & (12) \end{matrix}

(2) miatt

β' - α' = γ

: ha ez teljesül, ugyanez fennáll kotangenseikre is, azaz

ctg (β' - α') = ctg γ

. Felhasználva a kotangens addíciós képletét (nullával osztás nem fordul elő, mivel

0 < γ < π

\begin{matrix} \frac{cos γ}{sin γ} & = ctg γ = \frac{ctg α' ctg β' + 1}{ctg α' - ctg β'} = \frac{\frac{cos β - cos γ}{sin α} \frac{cos γ - cos α}{sin β} + 1}{\frac{cos β - cos γ}{sin α} - \frac{cos γ - cos α}{sin β}} = \\ = \frac{(cos β - cos γ) (cos γ - cos α) + sin α sin β}{(cos β - cos γ) sin β - (cos γ - cos α) sin α} = \\ = \frac{- cos β cos α + sin β sin α - cos^{2} γ + cos α cos γ + cos β cos γ}{sin α cos α + sin β cos β - sin α cos γ - sin β cos γ} = \\ = \frac{- cos (α + β) + cos γ (cos α + cos β - cos γ)}{\frac{1}{2} (sin 2 α + sin 2 β) - cos γ (sin α + sin β)} = \\ = \frac{cos γ (1 + cos α + cos β - cos γ)}{sin (α + β) cos (α - β) - cos γ (sin α + sin β)} = \\ = \frac{cos γ (1 + cos α + cos β - cos γ)}{sin γ cos (α - β) - cos γ (sin α + sin β)} . \end{matrix}

A bizonyítandóból tehát következik a következő egyenlet teljesülése:

\begin{matrix} \frac{cos γ}{sin γ} = \frac{cos γ (1 + cos α + cos β - cos γ)}{sin γ cos (α - β) - cos γ (sin α + sin β)} . \end{matrix}

(13)

(13) nyilván igaz akkor, ha

cos γ = 0

, azaz

γ

derékszög. Tegyük fel most, hogy

γ

nem derékszög, azaz oszthatunk

cos γ

-val: ezt elvégezve és felszorozva a nevezőkkel:

\begin{matrix} sin γ cos (α - β) - cos γ (sin α + sin β) = sin γ (1 + cos α + cos β - cos γ), \\ sin γ cos (α - β) = sin γ + (sin γ cos α + cos γ sin α) + \\ + (sin γ cos β + cos γ sin β) - sin γ cos γ = \\ = sin γ + sin (γ + α) + sin (γ + β) - sin γ cos γ = \\ = sin γ + sin β + sin α + sin γ cos (α + β), \\ sin γ (cos (α - β) - cos (α + β)) = sin α + sin β + sin γ, \\ sin γ \cdot 2 sin α sin β = sin α + sin β + sin γ . \end{matrix}

Az egyenlet mindkét oldalát beszorozzuk

R^{2}

-tel és alkalmazzuk a szinusztételt: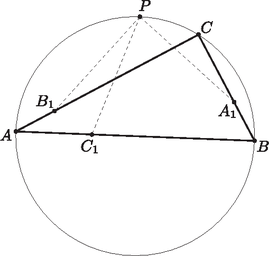

\begin{matrix} t = \frac{1}{2} a b sin γ = \frac{R}{2} (a + b + c) = R s; \end{matrix}

másrészt viszont ismert módon

t = ϱ s

és nyilván

R > ϱ

: ezek együtt ellentmondásra vezetnek, a háromszög tehát

C

-ben derékszögű. Ezt kellett bizonyítani.

Megjegyzés. Nem tettük fel, hogy

A P \neq B P

. Ha a háromszög

C

-ben derékszögű, valóban

\begin{matrix} ctg α' = \frac{cos β}{sin α} = 1 = \frac{cos α}{sin β} = ctg β', \end{matrix}

tehát

α' = β'

, így

A P = B P

. Az tehát, hogy a háromszögnek

C

-ben kell derékszögűnek lennie, az általánosság megszorításaiból (

P

elhelyezéséből és

C P \neq B P

feltevéséből) következik.

4. Legyen az

A B C

hegyesszögű háromszög magasságpontja

H

, és legyen

W

B C

oldal egy belső pontja. A

B

-ből, ill.

C

-ből induló magasságok talppontjai legyenek

M

, ill.

N

. Jelölje

ω_{1}

B W N

háromszög körülírt körét, és legyen

X

ω_{1}

kör azon pontja, amire

W X

ω_{1}

-nek átmérője. Hasonlóan, jelölje

ω_{2}

C W M

háromszög körülírt körét, és legyen

Y

ω_{2}

kör azon pontja, amire

W Y

ω_{2}

-nek átmérője. Bizonyítsuk be, hogy az

X

Y

és

H

pontok egy egyenesen fekszenek.

Fehér Zsombor megoldása. Miquel tétele szerint az

A B C

háromszög

A B

B C

C A

oldalegyenesein fekvő tetszőleges

N

W

M

pontokra a

B W N

C M W

, és

A N M

körök egy pontban metszik egymást. Ezt bebizonyíthatjuk a következőképpen:
Legyen a

B W N

és

C M W

körök második metszéspontja

P

. Húrnégyszögben a szemközti szögek összege

180^{\circ}

, így ha

P

A B C

háromszög belső pontja, akkor

\begin{matrix} M P N ∢ = 360^{\circ} - N P W ∢ - W P M ∢ = W B N ∢ + M C W ∢ = 180^{\circ} - B A C ∢ . \end{matrix}

Tehát

M P N ∢ = 180^{\circ} - N A M ∢

alapján

A N P M

is húrnégyszög. Irányított szögekkel számolva az előbbi bizonyítás működik akkor is, ha

P

külső pont.

B N C ∢ = B M C ∢ = 90^{\circ}

miatt a

B

N M

C

pontok egy körön vannak, legyen ez a kör

ω_{3}

. Ekkor az

ω_{1}

ω_{2}

és

ω_{3}

körök hatványvonalai egy ponton mennek át, tehát a

W P

egyenes átmegy

B N

és

C M

metszéspontján, az

A

ponton. Mivel

H N A ∢ = H M A ∢ = 90^{\circ}

, ezért

H

is rajta van az

A N M

körön, így

H P A ∢ = H M A ∢ = 90^{\circ}

. Amennyiben

H = P

, akkor a

H P

egyenest értelmezzük az

A N H P M

kör

H

-beli érintőjének.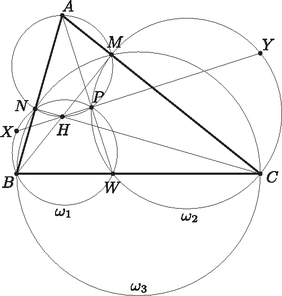

Mivel

W X

és

W Y

átmérő

ω_{1}

-ben és

ω_{2}

-ben, azért

W P X ∢ = W P Y ∢ = 90^{\circ}

. Ez pedig azt jelenti, hogy a

H

X

Y

pontok mind rajta vannak a

W A

-ra

P

-ben állított merőleges egyenesen.

5. Jelölje

Q_{> 0}

a pozitív racionális számok halmazát. Legyen

f : Q_{> 0} \to R

olyan függvény, ami kielégíti az alábbi három feltételt:

(i)

Minden

x, y \in Q_{> 0}

-ra

f (x) f (y) \geq f (x y)

;

(i i)

Minden

x, y \in Q_{> 0}

-ra

f (x + y) \geq f (x) + f (y)

;

(i i i)

Létezik olyan

a > 1

racionális szám, amire

f (a) = a

.
Bizonyítsuk be, hogy

f (x) = x

minden

x \in Q_{> 0}

-ra.

Janzer Olivér megoldása. Jelöljük

a

-val azt az (egyik) 1-nél nagyobb racionális számot, melyre

f (a) = a

(i)

-be

x = a

-t és

y = 1

-et helyettesítve

f (a) f (1) \geq f (a)

, azaz

a f (1) \geq a

. Mivel

a > 1

, azért leoszthatunk, így

f (1) \geq 1

. Bebizonyítjuk

n

szerinti teljes indukcióval, hogy ha

n

pozitív egész, akkor

f (n) \geq n

n = 1

-re igaz az állítás. Tegyük fel, hogy

n \leq k

-ig már beláttuk, bizonyítunk

n = k + 1

-re.

(i i)

-be

x = k

-t és

y = 1

-et helyettesítve

\begin{matrix} f (k + 1) \geq f (k) + f (1) \geq k + 1, \end{matrix}

így az indukciós lépést befejeztük. Tehát pozitív egész

n

-ekre

f (n) \geq n

.
Vegyünk egy tetszőleges

\frac{p}{q}

pozitív racionális számot (

p

és

q

pozitív egészek). Ekkor

(i)

-be

x = \frac{p}{q}

-t és

y = q

-t helyettesítve

\begin{matrix} f (\frac{p}{q}) f (q) \geq f (p) . \end{matrix}

f (q) \geq q

és

f (p) \geq p

, így

f (q)

és

f (p)

is pozitív. Így

f (\frac{p}{q})

is pozitív kell legyen. Tehát minden

x \in Q_{> 0}

-ra

f (x) > 0

. Így

(i i)

-ből

\begin{matrix} f (x + y) \geq f (x) + f (y) > f (y), \end{matrix}

tehát a függvény szigorúan monoton nő. (Ha

x_{1} > x_{2}

, akkor

x = x_{1} - x_{2}

y = x_{2}

helyettesítésekkel

f (x + y) > f (y)

-ból

f ([x_{1} - x_{2}] + x_{2}) > f (x_{2})

, azaz

f (x_{1}) > f (x_{2})

.)
Most

n

szerinti teljes indukcióval igazoljuk, hogy

f (a^{n}) \leq a^{n}

, ha

n

pozitív egész.

n = 1

esetén

f (a) = a \leq a

. Bizonyítunk

n = k

-ról

n = k + 1

-re.

(i)

-be

x = a^{k}

-t és

y = a

-t helyettesítve

f (a^{k}) f (a) \geq f (a^{k + 1})

. Így, mivel

f (a^{k}) \leq a^{k}

és

f (a) = a

, azért

f (a^{k + 1}) \leq a^{k + 1}

.
Tegyük fel, hogy valamilyen

x_{0} \in Q_{> 0}

esetén

f (x_{0}) > x_{0}

. Legyen ekkor

f (x_{0}) = x_{0} + c

, ahol

c > 0

n

szerinti teljes indukcióval igazoljuk, hogy

f (n x_{0}) \geq n x_{0} + n c

, ha

n

pozitív egész.

n = 1

-re valóban

f (x_{0}) = x_{0} + c \geq x_{0} + c

. Bizonyítunk

n = k

-ról

n = k + 1

-re.

(i i)

-be

x = k x_{0}

-t és

y = x_{0}

-t helyettesítve

\begin{matrix} f ([k + 1] x_{0}) \geq f (k x_{0}) + f (x_{0}) \geq (k x_{0} + k c) + (x_{0} + c) = (k + 1) x_{0} + (k + 1) c . \end{matrix}

Az indukciós lépést befejeztük,

f (n x_{0}) \geq n x_{0} + n c

.
Mivel

c

és

x_{0}

pozitív számok, így van olyan

K

pozitív szám, melyre

K c > x_{0}

. Minthogy

a > 1

, ezért van olyan

n

pozitív egész, amelyre teljesül

(K + 1) x_{0} < a^{n}

x_{0}

pozitív szám, így egyértelműen létezik olyan

k

egész, melyre

\begin{matrix} k x_{0} \leq a^{n} < (k + 1) x_{0} . \end{matrix}

Így

(K + 1) x_{0} < a^{n} < (k + 1) x_{0}

, amiből

K < k

. Így, mivel

K

pozitív, ezért

k

is, azaz

k

pozitív egész. Mivel

f

szigorúan monoton nő, ezért

k x_{0} \leq a^{n}

-ből

f (k x_{0}) \leq f (a^{n})

. Korábban belátott állításunk szerint viszont

f (k x_{0}) \geq k x_{0} + k c

, illetve

f (a^{n}) \leq a^{n}

, így

\begin{matrix} k x_{0} + k c \leq f (k x_{0}) \leq f (a^{n}) \leq a^{n} . \end{matrix}

Mivel

a^{n} < (k + 1) x_{0}

, azért

k x_{0} + k c < (k + 1) x_{0}

, amiből

k c < x_{0}

. Azonban

K < k

és

K c > x_{0}

, ami

c > 0

miatt ellentmond

k c < x_{0}

-nak. Így ellentmondásra jutottunk, azaz feltevésünkkel szemben nincsen olyan

x_{0} \in Q_{> 0}

, amelyre

f (x_{0}) > x_{0}

. Tehát

x \in Q_{> 0}

esetén

f (x) \leq x

.
Azt azonban tudjuk, hogy

f (n) \geq n

, ha

n

pozitív egész. Így

n \leq f (n) \leq n

, tehát

f (n) = n

. Vegyünk egy tetszőleges

\frac{p}{q}

pozitív racionális számot (

p

és

q

pozitív egészek). Ekkor

(i)

-be

x = \frac{p}{q}

-t és

y = q

-t helyettesítve azt kapjuk, hogy

\begin{matrix} f (\frac{p}{q}) f (q) \geq f (p) . \end{matrix}

Mivel

f (q) = q

és

f (p) = p

, azért

\begin{matrix} f (\frac{p}{q}) q \geq p, amiből f (\frac{p}{q}) \geq \frac{p}{q} . \end{matrix}

Ezt összevetve

f (x) \leq x

-szel azt kapjuk, hogy

f (\frac{p}{q}) = \frac{p}{q}

. Így a feladat állítását igazoltuk.

6. Legyen

n \geq 3

egész szám, és tekintsünk egy kört, amit

n + 1

ponttal egyenlő hosszúságú ívekre osztottunk. Tekintsük ezeknek a pontoknak a

0,1, ..., n

számokkal való összes olyan számozását, ahol minden számot pontosan egyszer használtunk; két ilyen számozást azonosnak tekintünk, ha egyiket a másikból megkaphatjuk a kör egy elforgatásával. Egy számozást szépnek nevezünk, ha bármely négy

a < b < c < d

számra, amikre

a + d = b + c

, fennáll az, hogy az

a

és

d

jelű pontokat összekötő húr nem metszi a

b

és

c

jelű pontokat összekötő húrt.
Legyen

M

a szép számozások száma, és legyen

N

a pozitív egészekből álló olyan

(x, y)

rendezett párok száma, amikre

x + y \leq n

és

lnko (x, y) = 1

teljesül. Bizonyítsuk be, hogy

\begin{matrix} M = N + 1. \end{matrix}

Nagy Róbert megoldása. Először olyan húrokat vizsgálunk, melyek végpontjain az összeg

k

‐ nevezzük ezeket

k

-húroknak.

Lemma. Egy szép elrendezésben bármely három húrra teljesül, hogy az egyik elválasztja a másik kettőt.

Bizonyítás. Indukcióval bizonyítunk

n

szerint. Ha

n \leq 3

, akkor az állítás triviális. Legyen

n \geq 4

, és bizonyítsunk indirekten.
Tegyük fel, hogy létezik három olyan húr, melyek ,,nem elválasztóak''. Legyenek a három húr végpontjai:

a b

c d

e f

, ahol ezek a végpontokra írt számokat is jelölik. Ekkor ha

n

nem szerepel a hat végpont között, akkor

n

-et elhagyva a körről továbbra is szép elrendezést kapunk, melyben csak

(n - 1)

-ig vannak az elemek. Erre már beláttuk, hogy teljesül az állítás, tehát ez ellentmondás. Ugyanígy, ha 0 nem szerepel a húr végpontok között, akkor ezt elhagyva és minden pont értékét eggyel csökkentve is szép elrendezéshez jutunk, melyben a legnagyobb elem megint csak

n - 1

, ami ellentmondás.
Tehát a 0 és az

n

elemek is a húrok végpontjai között vannak. Vegyük észre, hogy az

n

és a 0 azonos húrok végpontjai, különben:

n + b > n > 0 + d

, tehát

k = n

.
Legyen

A

B

C

a három húr, mely nem elválasztó. Ezek közül legyen

C

az, melynek két végpontja 0 és

n

. Ekkor vegyük azt a

D

húrt, mely közvetlenül a

C

húr mellett van, azonos oldalon az

A

és

B

húrokkal. Ennek két végpontja legyen

u

és

v

u + v = t

.
Ha

t = n

, akkor a

C

húr két végpontját elhagyva és az összes elemet eggyel csökkentve megint olyan elrendezést kapunk, amire már beláttuk az állítást az indukció miatt.
Ha

t < n

, akkor

t

nyilvánvalóan a

C

húr másik oldalán van, hiszen különben a

D

húr és a

{0, t}

húr metsző lenne. Így

(n - t)

(hiszen

t

n - t

nem metsző

C

-vel) is

C

másik oldalán van, ekkor viszont a

C

húr végpontjait elhagyva megint kapunk három húrt, melynek végpontjain a számok összege megegyező és nem szétválasztóak. De

(n - 2)

-re már beláttuk az állítást az indukció miatt.
Ha

t > n

, akkor vegyünk minden

x

szám helyett

n - x

-et. Vegyük észre, hogy ekkor az elrendezés nyilvánvalóan továbbra is szép lesz, és ekkor visszakapjuk az előző esetet. Tehát beláttuk, hogy minden elrendezésben a

k

-húrok szétválasztóak.

□

Bizonyítsuk az eredeti állítást teljes indukcióval.

n = 2

-re az állítás nyilvánvaló. Ezek után legyen

n \geq 3

. Legyen

S

egy szép elrendezés

0, ..., n

számozással. Ekkor ha

n

-et elhagyjuk, akkor kapunk egy

T

szép elrendezést

0, ..., n - 1

számozással. Az

n

-húrok

T

-ben szétválasztóak, így 0-n kívül minden pontnak van párja. Legyen

T

1-es típusú, ha 0 két

n

-húr között van, és legyen

T

2-es típusú, ha nem, tehát a 0-t egy húr választja el a többitől.
Megmutatjuk, hogy minden 1-es típusú

T

elrendezés pontosan egy

S

elrendezésből származik, míg minden 2-es típusú elrendezés 2 különböző 2-es

S

elrendezésből ered.
Ha

T

1-es típusú, akkor legyen 0 az

A

B

n

-húrok között. Mivel az

n

-húrok szétválasztóak, ezért a

T

elrendezésből egyértelműen visszakaphatjuk az

S

elrendezést, mivel az

n

pontnak

A

B

másik végpontjai közötti íven kell lennie. Ha belátjuk, hogy egy 1-es típusú

T

elrendezésbe a megfelelő helyre visszarakva

n

-t egy megfelelő

S

-t kapunk, akkor készen vagyunk, hiszen a másik irány nyilvánvaló. Ha

0 < k < n

, akkor nyilván teljesül az állítás, hiszen a

T

-ben levő

k

-húrok

S

-ben is azok.
Ha

n < k < 2 n

, akkor az

n

-húrok párhuzamosak az elrendezés miatt, tehát létezik egy

l

tengely, melyre

x

és

n - x

szimmetrikusak. Ha lenne két

k

-húr, mely metsző, akkor az

l

-re szimmetrikus párjai is metszők, de ezekben a húrok végén levő számok összege

2 n - k < n

, ami ellentmondás.
Ha

T

2-es típusú, akkor ugyanígy megy a bizonyítás, csak az

n

-et a 0 mindkét oldalára be tudjuk rakni, tehát kétszer annyi eset keletkezik.
Legyen

M_{n}

a szép elrendezések száma

0, ..., n

számozással, és legyen

L_{n}

a 2-es típusú szép elrendezések száma

0, ..., n

számozással. Ekkor

\begin{matrix} M_{n} = (M_{n - 1} - L_{n - 1}) + 2 L_{n - 1} = M_{n - 1} + L_{n - 1} . \end{matrix}

Tehát elég belátni az indukció miatt, hogy

L_{n - 1}

azon

(x, y)

párok száma, melyre

x + y = n

és

lnko (x, y) = 1

. Ahhoz, hogy ezt belássuk, vegyünk egy 2-es típusú szép elrendezést

0, ..., n - 1

számozással. Számozzuk a helyeket a

0,1,2, ..., (n - 1)

-gyel (mod

n

), mégpedig úgy, hogy a 0 elem a 0-s helyen legyen.
Legyen

F (i)

i

-edik pozícióban levő elem értéke.

f

egy permutációja a

[0, n - 1]

-nek. Legyen

f (a) = n - 1

. Mivel az

n

-húrok szétválasztóak 0-val, és minden pont valamely húrnak az eleme, azért az

n

-húrok párhuzamosak egymással, így

f (i) + f (- i) = n

minden

i

-re.
Mivel az

n - 1

húrok is szétválasztóak, és minden pont valamely húrnak az eleme, ezek a húrok is párhuzamosak, így

f (a - 1) = f (- i) - 1

minden

i

-re, és mivel

f (0) = 0

, azért

f (- a k) = k

minden

k

-ra. Ez egy egyenlőség modulo

n

, és

f

0, ..., n - 1

elemek egy permutációja, így

(a, n) = 1

. Tehát

L_{n - 1} \leq φ (n)

.
Már csak azt kell belátnunk, hogy ezek az esetek valóban megoldások. Ehhez vegyünk négy számot a körön, melyekre teljesül, hogy

w + y = x + z

. Ekkor a pozíciókra teljesül, hogy

(- a w) + (- a y) = (- a x) + (- a z)

, ami azt jelenti, hogy a

w y

és

x z

húrok párhuzamosak, tehát az elrendezés valóban szép, így beláttuk az állítást.

¹Forrás: imomath.com.