Cím:	Megoldásvázlatok a 2012/2. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Gerőcs László
Füzet:	2012/március, 134 - 139. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2012/2. sz. emelt szintű gyakorló feladataihoz   I. rész     1. Amikor Jancsi célba ért a mezei futóversenyen, akkor a helyszíni riporter megkérdezte tőle, hogy hányadik helyen végzett. Jancsi így válaszolt: ,,Ha az előttem végzők fele mögöttem végzett volna, akkor mögöttem ötször annyian lettek volna, mint előttem. Ha viszont a mögöttem befutók harmada előttem végzett volna, akkor $6$-tal többen végeztek volna előttem, mint mögöttem.'' Hány résztvevője volt a futóversenynek és hányadik helyen végzett Jancsi?  (12 pont)   Megoldás. Legyen $x$ a Jancsi előtt, és $y$ a mögötte végzettek száma. Ekkor az első feltétel alapján: $\begin{array}{c}{\displaystyle y+\frac{x}{2}=5\cdot \left(x-\frac{x}{2}\right)\mathrm{,}\text{azaz}y=2x\mathrm{.}}\end{array}$ A második feltétel alapján: $\begin{array}{c}{\displaystyle y-\frac{y}{3}=x+\frac{y}{3}-\mathrm{6,}\text{azaz}\frac{y}{3}=x-6.}\end{array}$ A két egyenletből kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{2x}{3}=x-\mathrm{6,}\text{vagyis}x=18.}\end{array}$ Ezek szerint Jancsi előtt 18-an, mögötte 36-an végeztek. A versenyen résztvevők száma $18+1+36=55$. Jancsi a 19. helyen végzett.     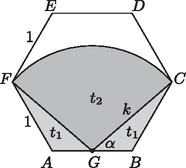2. Egy szabályos hatszög alakú rét egyik oldalának felezőpontjába szúrt karóhoz kikötöttünk egy kecskét. Hány százalékát legelheti le a kecske a rétnek, ha feszes kötél esetén pont el tud jutni a két szomszédos oldal távolabbi végpontjába?  (12 pont)   Megoldás. Legyen az $ABCDEF$ szabályos hatszög egységnyi oldalú. Ekkor területe: $\begin{array}{c}{\displaystyle T_{ABCDEF}=6\cdot \frac{\sqrt[]{3}}{4}\approx 2\mathrm{,}598.}\end{array}$     A kecske által elérhető területet két egybevágó háromszög és egy körcikk alkotja. Az $AGF$ és a $BGC$ háromszögek $t_1$ területe a trigonometrikus területképlet alapján: $\begin{array}{c}{\displaystyle t_1=\frac{1\cdot \frac{1}{2}\cdot \text{sin}{120}^{\circ }}{2}=\frac{\sqrt[]{3}}{8}\mathrm{.}}\end{array}$ Az $AGF$ háromszögre a koszinusztételt alkalmazva: $\begin{array}{c}{\displaystyle k^2=1+\frac{1}{4}-2\cdot 1\cdot \frac{1}{2}\cdot \text{cos}{120}^{\circ }=\frac{5}{4}+\frac{1}{2}=\frac{7}{4}\mathrm{,}\text{ahonnan}k=\frac{\sqrt[]{7}}{2}\mathrm{.}}\end{array}$ Az $AGF$ háromszögben a szinusztételből: $\begin{array}{c}{\displaystyle \frac{\text{sin}\alpha }{\text{sin}{120}^{\circ }}=\frac{1}{\frac{\sqrt[]{7}}{2}}=\frac{2}{\sqrt[]{7}}\mathrm{,}\text{tehát}\text{sin}\alpha =\frac{\sqrt[]{3}}{2}\cdot \frac{2}{\sqrt[]{7}}=\sqrt[]{\frac{3}{7}}\mathrm{,}\text{ahonnan}\alpha \approx 40\mathrm{,}{9}^{\circ }\mathrm{.}}\end{array}$ Ezek szerint a körcikk $FGC$ középponti szöge: $FGC={180}^{\circ }-2\cdot {40\mathrm{,}9}^{\circ }={98\mathrm{,}2}^{\circ }$. Vagyis a körcikk $t_2$ területe: $\begin{array}{c}{\displaystyle t_2=\frac{k^2\pi }{360}\cdot 98\mathrm{,}2\approx 1\mathrm{,}5.}\end{array}$ A kecske által elérhető rész $T$ területe: $\begin{array}{c}{\displaystyle T=2t_1+t_2=\frac{\sqrt[]{3}}{4}+1\mathrm{,}5\approx 1\mathrm{,}933.}\end{array}$ Tehát a kecske a rét $\frac{1\mathrm{,}933}{2\mathrm{,}598}\cdot 100\approx 0\mathrm{,}744$-ed részét, azaz 74,4%-át tudja lelegelni.     3. Legyen az alaphalmaz az első $n$ pozitív egész számot tartalmazó halmaz. Legyen az $A$ halmaz a $3$-mal osztható, a $B$ halmaz a $4$-gyel osztható, a $C$ halmaz pedig az $5$-tel osztható számok halmaza. $a)$ Véletlenszerűen kiválasztva egy számot, mekkora annak a valószínűsége, hogy az a megadott három halmaz egyikének sem eleme, ha $n=100?$ $b)$ Ha az $A\cap B\cap C$ halmaznak $2$ eleme van, akkor hány eleme lehet az $\left(A\cap B\right)\backslash C$ halmaznak?  (13 pont)   Megoldás. $a)$ Az $A\cap B\cap C$ halmaznak csak 1 darab eleme van (ez a 60). Legyen az $A\cap B$ elemeinek száma $x$, a $B\cap C$ elemeinek száma $y$, az $A\cap C$ elemeinek száma pedig $z$. Az $A$ halmaz elemei a 100-nál nem nagyobb 3-mal osztható pozitív egész számok. Ezek egy olyan számtani sorozat egymást követő tagjai, melynek első tagja 3, utolsó tagja 99, differenciája 3, tehát $99=3+\left(n-1\right)\cdot 3$, ahonnan $n=33$. Tehát az $A$ halmaznak 33 eleme van. Hasonlóképpen kapjuk, hogy a $B$ halmaznak 25, a $C$ halmaznak pedig 20 eleme van. Ezek szerint a felhasznált számok száma: $\begin{array}{c}{\displaystyle 33+25+20-\left(x+y+z\right)+1.}\end{array}$ Az $A\cap B$ halmazba a 12-vel osztható számok tartoznak: $\begin{array}{c}{\displaystyle A\cap B=\left\{\mathrm{12,24,36,48,60,72,84,96}\right\}\mathrm{.}}\end{array}$ Tehát ennek a halmaznak 8 eleme van, azaz $x=8$. A $B\cap C$ halmazba a 20-szal osztható számok tartoznak: $\begin{array}{c}{\displaystyle B\cap C=\left\{\mathrm{20,40,60,80,100}\right\}\mathrm{.}}\end{array}$ Tehát ennek a halmaznak 5 eleme van, azaz $y=5$. A $A\cap C$ halmazba a 15-tel osztható számok tartoznak: $\begin{array}{c}{\displaystyle A\cap C=\left\{\mathrm{15,30,45,60,75,90}\right\}\mathrm{.}}\end{array}$ Tehát ennek a halmaznak 6 eleme van, azaz $z=6$. Ezek szerint a felhasznált számok száma: $33+25+20-\left(8+5+6\right)+1=60$. Így azon számok száma, melyeket egyetlen halmazba sem soroltunk be, 40. A keresett valószínűség: $\frac{40}{100}=0\mathrm{,}4$. $b)$ Ha az $A\cap B\cap C$ halmaznak 2 eleme van, akkor azok csak a 60 és a 120 lehetnek. Az $\left(A\cap B\right)\backslash C$ halmazba a 12-vel osztható, 180-nál kisebb, $n$-nél nem nagyobb, pozitív egész számok tartoznak, kivéve a 60-at és a 120-at. Ezek szerint: $12\le 12k<180$, ahol $k$ egész szám, de $k\ne 5$, $k\ne 10$. A $k$ lehetséges értékei: 1, 2, 3, 4, 6, 7, 8, 9 (ezek mindenképpen), 11, 12, 13, 14 (ezek az $n$ értékétől függően). Vagyis az $\left(A\cap B\right)\backslash C$ halmaz elemeinek száma 8, 9, 10, 11 vagy 12 lehet.     4. A MÁV statisztikai adatai szerint az utazók $8\%$-a bliccel (azaz érvényes jegy nélkül utazik). $a)$ Egy vagonban $24$ utas tartózkodik. Mekkora annak az esélye, hogy a jegyellenőr talál bliccelőt a vagonban? $b)$ Hány utas esetén lesz legalább $90\%$ annak az esélye, hogy a jegyellenőr talál bliccelőt a vagonban?  (14 pont)   Megoldás. $a)$ Annak a valószínűsége, hogy egy utas bliccel, 0,08, így annak a valószínűsége, hogy egy utasnak van érvényes jegye, 0,92. Számítsuk ki annak a valószínűségét, hogy a jegyellenőr nem talál bliccelőt. Ennek valószínűsége: $0\mathrm{,}{92}^{24}\approx 0\mathrm{,}1352$. Annak a valószínűsége, hogy a 24 utas között találunk bliccelőt: $1-0\mathrm{,}1352=0\mathrm{,}8648$. Tehát kb. 86,5% annak az esélye, hogy a 24 utas között találunk bliccelőt. $b)$ Ha annak az esélye legalább 90%, hogy az ellenőr talál bliccelőt a vagonban, az egyben azt is jelenti, hogy annak az esélye, hogy nem talál bliccelőt, 10%-nál kisebb. Ha ez $n$ utasra teljesül, akkor $0\mathrm{,}{92}^n<0\mathrm{,}1$. Vegyük az egyenlőtlenség mindkét oldalának 10-es alapú logaritmusát: $\text{lg}0\mathrm{,}{92}^n<\text{lg}0\mathrm{,}1$, azaz $n\cdot \text{lg}0\mathrm{,}92<\text{lg}0\mathrm{,}1$. Mivel $\text{lg}0\mathrm{,}92<0$, azért $\begin{array}{c}{\displaystyle n>\frac{\text{lg}0\mathrm{,}1}{\text{lg}0\mathrm{,}92}\approx 27\mathrm{,}62.}\end{array}$ Tehát ha $n\ge 28$, akkor már legalább 90% annak az esélye, hogy az ellenőr talál bliccelőt a vagonban.   II. 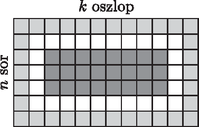rész     5. Egy egységnyi négyzetekből álló négyzetrács $n$ sorból és $k$ oszlopból áll. A négyzetrács szélével érintkező négyzetek száma (az ábrán világosszürke), a négyzetrács szélével érintkező négyzetekkel érintkező négyzetek száma (az ábrán fehér), és a négyzetrács belsejében levő négyzetek száma (az ábrán sötétszürke) egy számtani sorozat egymást követő tagjai. Határozzuk meg $n$ és $k$ értékét.  (16 pont)       Megoldás. A feltételekből következik, hogy $n>4$ és $k>4$. A négyzetrács szélén levő négyzetek száma: $a_1=2k+2n-4$. A szélével érintkező négyzetekkel érintkező négyzetek száma: $a_2=2\left(k-2\right)+2\left(n-2\right)-4=2k+2n-12$. Az összes többi négyzetek száma: $a_3=\left(k-4\right)\left(n-4\right)$. A számtani sorozat differenciája: $a_2-a_1=-8$. Ezek szerint: $\begin{array}{c}{\displaystyle a_3-a_2=\left(k-4\right)\left(n-4\right)-2k-2n+12=-\mathrm{8,}}\end{array}$ azaz $kn-6n-6k+36=0$, ahonnan $\left(k-6\right)\left(n-6\right)=0$. Ez akkor és csak akkor teljesül, ha $k=6$ vagy $n=6$. Ezek szerint a feladat feltételei akkor teljesülnek, ha a négyzetrács valamelyik oldala 6, a másik pedig tetszőleges, 4-nél nagyobb pozitív egész szám.     6. Milyen pozitív egész $n$-re teljesül, hogy a $\frac{3\sqrt[]{n}+\sqrt[]{3}}{4\sqrt[]{3}-\sqrt[]{n}}$ tört értéke pozitív egész szám?   (16 pont)   Megoldás. Legyen $k$ az a pozitív egész szám, melyre ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{3\sqrt[]{n}+\sqrt[]{3}}{4\sqrt[]{3}-\sqrt[]{n}}}& {\displaystyle =k\mathrm{,}\text{azaz}}\hfill \\ \hfill {\displaystyle 3\sqrt[]{n}+\sqrt[]{3}}& {\displaystyle =4k\sqrt[]{3}-k\sqrt[]{n}\mathrm{,}}\hfill \\ \hfill {\displaystyle \sqrt[]{n}\cdot \left(3+k\right)}& {\displaystyle =\sqrt[]{3}\cdot \left(4k-1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{4k-1}{3+k}}& {\displaystyle =\sqrt[]{\frac{n}{3}}\mathrm{.}}\hfill \end{array}}$ A bal oldalon egy racionális szám szerepel. A jobb oldal akkor és csak akkor lesz racionális, ha a négyzetgyök alatt egy racionális szám négyzete szerepel, azaz $n=3r^2$ alakú, ahol $r$ egy pozitív egész szám. Ekkor $\frac{4k-1}{3+k}=r$. Alakítsuk át a bal oldalt a következő módon: $\begin{array}{c}{\displaystyle \frac{4k-1}{3+k}=\frac{4k+12-13}{3+k}=\frac{4k+12}{3+k}-\frac{13}{3+k}=4-\frac{13}{3+k}\mathrm{.}}\end{array}$ Ez akkor és csak akkor lesz egész szám, ha $3+k$ osztója 13-nak, azaz $3+k=1$, $-1$, 13 vagy $-13$. Ezen esetek közül csak $3+k=13$ esetén adódik $k$-ra pozitív egész   érték. Vagyis $k=10$. Ezzel $\frac{39}{13}=\sqrt[]{\frac{n}{3}}$, ahonnan $n=27$.     7. A Budapest‐Zürich nemzetközi gyorsvonat szerelvénye $12$ vagonból áll: 4 db $1$. osztályú, 6 db $2$. osztályú vagon, valamint egy étkezőkocsi és egy poggyászkocsi. $a)$ Hányféleképpen alakulhat a kocsik sorrendje oly módon, hogy az $1$. osztályú kocsik is és a $2$. osztályú kocsik is egymás mögött legyenek, és az étkezőkocsi ne legyen a szerelvény utolsó vagonja? 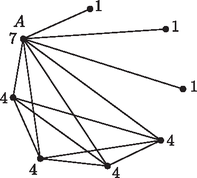$b)$ Az egyik vagonban $8$ tudós utazott, akik közül néhányan már ismerték egymást. Az egyik tudós (legyen a neve $A$) mindenkit ismert a társaságból. Három olyan tudós volt közöttük, akik $A$-n kívül senki mást nem ismertek, míg a többi négy ismerte egymást. Kézfogással bemutatkoztak azok, akik nem ismerték egymást. Hány kézfogás történt?  (16 pont)   Megoldás. $a)$ A 4-féle kocsit (étkező-, poggyász-, 1. osztályú, 2. osztályú kocsi) $4!$-féleképpen rakhatjuk sorba. E permutációk bármelyike $6!\cdot 4!$-féleképpen valósulhat meg, hiszen az 1. osztályú kocsikat 4!-féleképpen, a 2. osztályú kocsikat pedig 6!-féleképpen állíthatjuk sorba. Ezek szerint a sorbarendezések száma: $4!\cdot 4!\cdot 6!$. Ebből viszont még le kell vonnunk azokat az eseteket, amikor az étkezőkocsi a szerelvény utolsó vagonja. Ez összesen $3!\cdot 4!\cdot 6!$-féleképpen lehetséges. Tehát minden feltételt figyelembe véve a vagonok sorrendjének a száma: $\begin{array}{c}{\displaystyle 4!\cdot 4!\cdot 6!-3!\cdot 4!\cdot 6!=3!\cdot 4!\cdot 6!\cdot \left(4-1\right)=311040.}\end{array}$ $b)$ Szemléltessük egy gráffal az ismeretségeket. Írjuk a gráf minden csúcsa mellé a fokszámát. Az $A$ tudósnak megfelelő csúcs fokszáma 7. Mivel 3 olyan személy van, akik $A$-n kívül senkit sem ismernek, azért e három csúcs fokszáma 1. A további négy személy tagjai kölcsönösen ismerik egymást, ezért a nekik megfelelő csúcsok fokszáma 4. Ezek szerint a fokszámok összege: $\begin{array}{c}{\displaystyle 7+1+1+1+4+4+4+4=26.}\end{array}$     Mivel a gráf éleinek száma a fokszámok összegének a fele, azért a gráfnak 13 éle van. A kézfogások száma a hiányzó élek számával egyenlő. Mivel a 8 pontú teljes gráf éleinek száma $\frac{8\cdot 7}{2}=28$ és a gráfnak 13 éle van, azért a hiányzó élek (vagyis a kézfogások) száma $28-13=15$.     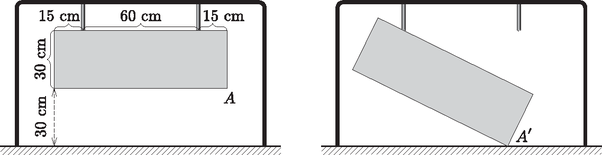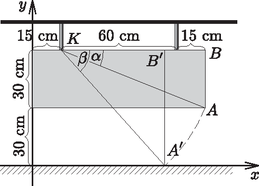8. Egy étterem bejárata előtt, vízszintes talajon egy fémkeretre függőleges rudakat hegesztettek, majd a rudakra csavarozott táblán hirdették a napi menüt. Egy idő után az egyik csapágy eltört (lásd ábra), és így a tábla a földre billent.     $a)$ Határozzuk meg a tábla $A$ csúcspontjának billenés utáni $A\text{'}$ helyzetét a földön. $b)$ Hány fokkal fordult el a tábla a billenés következtében?  (16 pont)   Megoldás. $a)$ Helyezzük el az ábrát egy koordinátarendszerbe. Legyen az $x$ tengely a talaj, az $y$ tengely pedig illeszkedjen a tábla bal oldali, függőleges széléhez. Billenéskor a tábla az épen maradt rúd $K$ végpontja körül forog. Így az $A$ pont egy olyan kör mentén forog, melynek középpontja $K$, sugara pedig a $KA$ szakasz hossza. Ami a valóságban 10 cm, az a koordinátarendszerben legyen 1 egység. Vagyis   $K\left(1\mathrm{,}5;6\right)$, a kör sugara: $AK=\sqrt[]{7\mathrm{,}{5}^2+3^2}=\sqrt[]{65\mathrm{,}25}$.     A kör egyenlete: $\begin{array}{c}{\displaystyle {\left(x-1\mathrm{,}5\right)}^2+{\left(y-6\right)}^2=65\mathrm{,}25.}\end{array}$ Az $A\text{'}$ pont a körnek az $x$ tengellyel való metszéspontja. Ezt megkapjuk, ha a kör egyenletébe $y=0$-t helyettesítünk. Ekkor ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(x-1\mathrm{,}5\right)}^2+36=65\mathrm{,}\mathrm{25,}\text{azaz}{\left(x-1\mathrm{,}5\right)}^2=29\mathrm{,}\mathrm{25,}}\hfill \\ \hfill {\displaystyle x-1\mathrm{,}5=\sqrt[]{29\mathrm{,}25}\mathrm{,}\text{vagy}x-1\mathrm{,}5=-\sqrt[]{29\mathrm{,}25}\mathrm{.}}\hfill \end{array}}$ Innen: $x_1=1\mathrm{,}5+\sqrt[]{29\mathrm{,}25}\approx 6\mathrm{,}9$, $x_2\approx -3\mathrm{,}9$. A negatív gyök nyilván érdektelen, így azt kaptuk, hogy $x\approx 6\mathrm{,}9$. Tehát az $A\text{'}$ pont a földön az eredetileg még ép tábla bal oldali függőleges egyenesétől kb. 69 cm-re van. $b)$ Billenéskor az elfordulás szöge az ábrán az $AKA\text{'}\sphericalangle =BKA\text{'}\sphericalangle -BKA\sphericalangle =\beta -\alpha$. $\alpha$ értékét a $BKA$ derékszögű háromszögből kaphatjuk meg (most már cm-ekben számolva): $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{AB}{BK}=\frac{30}{75}=0\mathrm{,}\mathrm{38,}\text{ahonnan}\alpha \approx {21\mathrm{,}8}^{\circ }\mathrm{.}}\end{array}$ $A\text{'}$ vetülete $KB$-re legyen $B\text{'}$. Így $\beta$ értékét az $B\text{'}KA\text{'}$ derékszögű háromszögből kaphatjuk meg: $\begin{array}{c}{\displaystyle \text{tg}\beta =\frac{A\text{'}B\text{'}}{B\text{'}K}=\frac{60}{69-15}=\frac{60}{54}\approx 0\mathrm{,}\mathrm{84,}\text{ahonnan}\beta \approx {48}^{\circ }\mathrm{.}}\end{array}$ Tehát a tábla a billenés következtében $48-21\mathrm{,}8=26\mathrm{,}2$ fokkal fordult el.     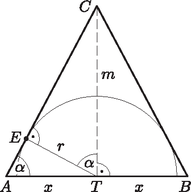9. Egy egyenlő szárú háromszög alapjának felezőpontja körül olyan félkört rajzoltunk, mely érinti a háromszög szárait. Mekkorák a háromszög szögei, ha a félkör területe a háromszög területének a lehető legnagyobb százalékát teszi ki?  (16 pont)   Megoldás. Használjuk az ábra jelöléseit. Ha a háromszög alapon fekvő szöge $\alpha$, akkor $ETC\sphericalangle =\alpha$, hiszen $EAT\sphericalangle$ és $ETC\sphericalangle$ merőleges szárú hegyesszögek. Az $EAT$ derékszögű háromszögben   $\text{sin}\alpha =\frac{r}{x}$, ahonnan $x=\frac{r}{\text{sin}\alpha }$.   Az $ETC$ derékszögű háromszögben $\text{cos}\alpha =\frac{r}{m}$, ahonnan $m=\frac{r}{\text{cos}\alpha }$. A háromszög területe: $\begin{array}{c}{\displaystyle T_{ABC}=\frac{2xm}{2}=xm=\frac{r^2}{\text{sin}\alpha \text{cos}\alpha }\mathrm{.}}\end{array}$       A félkör területe: $T_{\text{félkör}}=\frac{r^2\pi }{2}$. A félkör és a háromszög területének hányadosa az $\alpha$ hegyesszög függvényében: $\begin{array}{c}{\displaystyle H\left(\alpha \right)=\frac{\frac{r^2\pi }{2}}{\frac{r^2}{\text{sin}\alpha \text{cos}\alpha }}=\frac{\pi }{2}\text{sin}\alpha \text{cos}\alpha \mathrm{.}}\end{array}$ Ennek akkor lehet szélsőértéke, ha a deriváltja 0. $\begin{array}{c}{\displaystyle H\text{'}\left(\alpha \right)=\frac{\pi }{2}\cdot \left[\left(\text{sin}\alpha \right)\text{'}\text{cos}\alpha +\left(\text{cos}\alpha \right)\text{'}\text{sin}\alpha \right]=\frac{\pi }{2}\cdot \left[\text{cos}{}^2\alpha -\text{sin}{}^2\alpha \right]=0.}\end{array}$ Mivel $\alpha$ hegyesszög, azért $\text{sin}\alpha =\text{cos}\alpha$, ahonnan $\alpha ={45}^{\circ }$. A kapott érték valóban szélsőérték és maximum, hiszen $\alpha <{45}^{\circ }$ esetén $H\text{'}\left(\alpha \right)>0$, $\alpha >{45}^{\circ }$ esetén pedig $H\text{'}\left(\alpha \right)<0$. Vagyis a keresett háromszög szögei: ${45}^{\circ }$, ${45}^{\circ }$, ${90}^{\circ }$. Megjegyzés. Természetesen, az addíciós tételek ismeretében a következő átalakítással, deriválás nélkül is ugyanehhez az eredményhez juthattunk volna: $\begin{array}{c}{\displaystyle H\left(\alpha \right)=\frac{\pi }{2}\text{sin}\alpha \text{cos}\alpha =\frac{\pi }{4}2\text{sin}\alpha \text{cos}\alpha =\frac{\pi }{4}\text{sin}2\alpha \mathrm{.}}\end{array}$   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Gerőcs László</span><br>Budapest}}\hfill \end{array}}$