Kezdőlap


Cím:	Megoldásvázlatok a 2011/7. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2011/november, 468 - 474. oldal	PDF \| MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldásvázlatok a 2011/7. sz. emelt szintű gyakorló feladataihoz

I. rész

1. Adjuk meg a következő egyenletek valós megoldásait:

a)

{(x + 500)}^{2} = 252 012 - 1011 x

;

b)

lg^{2} x + 2011 \cdot lg x - 2012 = 0

;

c)

x + 2011 \sqrt[]{x - 7} - 2019 = 0

. (11 pont)

Megoldás.

a)

Végezzük el a négyzetre emelést és rendezzük nullára az egyenletet:

\begin{matrix} x^{2} + 2011 x - 2012 = 0. \end{matrix}

A gyökök és együtthatók közötti összefüggés alkalmazásával vagy megoldóképlettel (

x_{1} + x_{2} = - 2011

x_{1} x_{2} = - 2012)

gyorsan megkapható, hogy

x_{1} = 1

x_{2} = - 2012

b)

Az egyenlet

lg x

-re másodfokú, az értelmezési tartománya:

x > 0

. A két lehetséges érték

lg x

-re

a)

megoldása alapján:

{(lg x)}_{1} = 1

{(lg x)}_{2} = - 2012

. Vagyis:

x_{1} = 10

x_{2} = 10^{- 2012}

. Mindkettő megoldása az egyenletnek, mert benne van az értelmezési tartományban.

c)

Az értelmezési tartomány:

x \geq 7

. A következő alakban is írhatjuk a megadott egyenletet:

\begin{matrix} x - 7 + 2011 \sqrt[]{x - 7} - 2012 = 0. \end{matrix}

Másodfokú egyenletet kaptunk

\sqrt[]{x - 7}

-re. A két lehetséges érték

\sqrt[]{x - 7}

-re:

{(\sqrt[]{x - 7})}_{1} = 1

{(\sqrt[]{x - 7})}_{2} = - 2012

. Az első esetben

x = 8

, a második esetben nincs megfelelő

x

. Az

x = 8

megoldása az egyenletnek, mert benne van az értelmezési tartományban.

2. Egy mértani sorozat első eleme

2

. Ha a sorozat második elemét

20

-szal csökkentjük, a harmadik elemét pedig az első kettő elé írjuk, akkor egy számtani sorozat három, egymást követő tagját kapjuk. Adjuk meg az eredeti három számot. (12 pont)

Megoldás. Legyen a mértani sorozat hányadosa

q

, ekkor a feladatban szereplő három tag: 2;

2 q

;

2 q^{2}

. A szöveg alapján a

2 q^{2}

; 2;

2 q - 20

egy számtani sorozat három, egymást követő tagja lesz, azaz:

2 - 2 q^{2} = 2 q - 20 - 2

. Rendezéssel a

0 = q^{2} + q - 12

másodfokú egyenletet kapjuk, amelyből:

q_{1} = 3

q_{2} = - 4

.
Két megfelelő számhármast találtunk. Megoldás a 2; 6; 18, illetve a 2;

- 8

; 32.

3. Az

A B C

egyenlőszárú háromszögben

A B = 6

C F = 9

, ahol

F

A B

alap felezőpontja. Az

A

csúcstól indulva és a körüljárási irányt tartva az oldalakon a harmadoló pontok:

A_{1}

A_{2}

B_{1}

B_{2}

C_{1}

C_{2}

. Mekkora a

C_{1} B_{1}

C_{2} B_{2}

C_{1} A_{2}

A_{1} B_{2}

egyenesek által meghatározott négyszög területe? (14 pont)

Megoldás. Az

A B C

háromszöget tegyük koordinátarendszerbe a következő módon:

A (- 3; 0)

B (3; 0)

C (0; 9)

. A feladatban szereplő harmadoló pontok koordinátáit is meg tudjuk adni:

A_{1} (- 1; 0)

A_{2} (1; 0)

B_{1} (2; 3)

B_{2} (1; 6)

C_{1} (- 1; 6)

C_{2} (- 2; 3)

.
A harmadoló pontok ismeretében a megfelelő egyenesek egyenlete felírható, hiszen minden kérdéses egyenes két pontjával adott.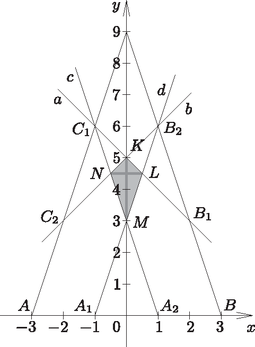

C_{1}

és a

B_{1}

pontokra illeszkedő

a

egyenes egyenlete:

y = - x + 5

.
A

C_{2}

és a

B_{2}

pontokra illeszkedő

b

egyenes egyenlete:

y = x + 5

.
Az

A_{2}

és a

C_{1}

pontokra illeszkedő

c

egyenes egyenlete:

y = - 3 x + 3

.
Az

A_{1}

és a

B_{2}

pontokra illeszkedő

d

egyenes egyenlete:

y = 3 x + 3

.
Meghatározzuk a megfelelő metszéspontok koordinátáit.
Az

a

és

b

metszéspontja:

K (0; 5)

.
A

c

és

d

metszéspontja:

M (0; 3)

.
Az

a

és

d

metszéspontja:

L (\frac{1}{2}; \frac{9}{2})

.
Az ábra szimmetriája miatt
a

c

és

b

metszéspontja:

N (- \frac{1}{2}; \frac{9}{2})

. A szimmetria miatt

K L M N

négyszögről belátható, hogy deltoid.
Csúcsainak ismeretében az átlók hossza:

K M = 2

N L = 1

. Vagyis a kérdéses terület:

t_{K L M N} = \frac{1 \cdot 2}{2} = 1

4. Az

A B C D

téglalap alakú

20^{\circ}

-os emelkedő alsó, vízszintes,

20

méter hosszúságú

A B

oldalának az

A

csúcsából egy egyenes mentén szeretnénk feljutni a

C D

oldal valamely pontjába. Ezeknek a párhuzamos oldalaknak

12

méter a távolsága. Hová érkezhetünk, ha az útvonal vízszintessel bezárt hajlásszöge nem haladhatja meg a

12^{\circ}

-ot? (14 pont)

Megoldás. A szöveg alapján készítsünk ábrát.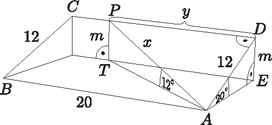

A E D

derékszögű háromszögben

sin 20^{\circ} = \frac{m}{12}

, azaz

m = 12 \cdot sin 20^{\circ} \approx 4, 10

.
Az

A T P

derékszögű
háromszögben

sin 12^{\circ} = \frac{m}{x} = \frac{4, 1}{x}

, azaz

x = \frac{4, 1}{sin 12^{\circ}} \approx 19, 72

.
Végül az

A D P

derékszögű háromszögben

\begin{matrix} y = \sqrt[]{x^{2} - 12^{2}} = \sqrt[]{19, 72^{2} - 12^{2}} \approx 15, 65. \end{matrix}

Vagyis ha

D P \geq 15, 65

m, akkor

A P

vízszintessel bezárt hajlásszöge nem nagyobb, mint

12^{\circ}

II. rész

5.Tekintsük a

K (5; 2)

középpontú,

r = 3

egység sugarú

k

kört. Az origóból az

e_{1}

és az

e_{2}

érintők húzhatók a

k

körhöz.

a)

Írjuk fel

e_{1}

és

e_{2}

egyenletét.

b)

Mekkora szöget zár be egymással

e_{1}

és

e_{2}

c)

Mekkora területű az a síkidom, amelynek pontjaiból a

k

kör

60^{\circ}

-nál nem kisebb,

90^{\circ}

-nál pedig nem nagyobb szögben látható? (16 pont)

Megoldás.

a)

k

kör egyenlete:

{(x - 5)}^{2} + {(y - 2)}^{2} = 9

. Az origóra illeszkedő egyenesek egyenlete:

y = m x

. Ezek közül az lesz az érintő, amelynek a körrel pontosan egy közös pontja van. Tehát az

\begin{matrix} \begin{matrix} {(x - 5)}^{2} + {(y - 2)}^{2} = 9, \\ y = m x \end{matrix}} \end{matrix}

paraméteres egyenletrendszerben azokat az

m

paramétereket keressük, amelyekre az egyenletrendszernek csak egyféle megoldása van.
Végezzük el a behelyettesítést:

\begin{matrix} {(x - 5)}^{2} + {(m x - 2)}^{2} & = 9, \\ x^{2} - 10 x + 25 + m^{2} x^{2} - 4 m x + 4 & = 9, \\ (m^{2} + 1) x^{2} - (4 m + 10) x + 20 & = 0. \end{matrix}

A keresett

m

értékeket akkor kapjuk, ha a fenti paraméteres másodfokú egyenletben:

\begin{matrix} D = {(4 m + 10)}^{2} - 80 (m^{2} + 1) = 0, \\ 16 m^{2} + 80 m + 100 - 80 m^{2} - 80 = 0, \\ 16 m^{2} - 20 m - 5 = 0. \\ m_{1; 2} = \frac{20 \pm \sqrt[]{400 + 320}}{32} = \frac{20 \pm \sqrt[]{720}}{32} = \frac{5 \pm 3 \sqrt[]{5}}{8} . \end{matrix}

A keresett két érintő egyenlete:

e_{1} : y = \frac{5 + 3 \sqrt[]{5}}{8} x

e_{2} : y = \frac{5 - 3 \sqrt[]{5}}{8} x

b)

Legyen az

e_{1}

érintőn

E_{1}

, az

e_{2}

érintőn

E_{2}

az érintési pont. A két érintő hajlásszöge az

E_{1} O E_{2} ∢

, ami az

O K E_{1}

derékszögű háromszög

O

-nál lévő

φ

hegyesszögnek a kétszerese. Az origó és a

K

középpont távolságát ki tudjuk számolni:

O K = \sqrt[]{5^{2} + 2^{2}} = \sqrt[]{29}

. Tudjuk, hogy

E_{1} K = 3

, ezért

sin φ = \frac{3}{\sqrt[]{29}}

.
Ebből kapjuk:

φ \approx 33, 85^{\circ}

, a hajlásszög pedig: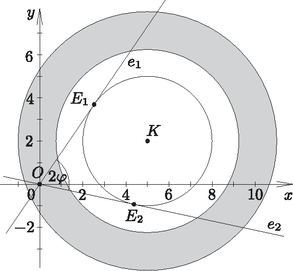

2 φ \approx 67, 7^{\circ}

Megjegyzés. A hajlásszöget természetesen a két meredekség ismeretében is meg tudnánk határozni, most azonban egy olyan gondolatmenetet láttunk, amely nem épült az előző kérdésre adott válaszra.

c)

Ha egy

P

pontból a kör

60^{\circ}

-os szögben látható, jelölje

R_{1}

P

-ből húzott egyik érintő érintési pontját. Ekkor a

K P R_{1}

derékszögű háromszögben

K R_{1} = 3

K P = 6

. Vagyis az ilyen

P

pontok halmaza egy

K

középpontú, 6 sugarú körvonal lesz.
Ha egy

Q

pontból a kör

90^{\circ}

-os szögben látható, jelölje

T_{1}

Q

-ból húzott egyik érintő érintési pontját. Ekkor a

K Q T_{1}

derékszögű háromszögben

K T_{1} = 3

K Q = 3 \sqrt[]{2}

. Vagyis az ilyen

Q

pontok halmaza egy

K

középpontú,

3 \sqrt[]{2}

sugarú körvonal lesz.
A megfelelő pontok e két körvonal által meghatározott körgyűrű pontjai lesz- nek.
Ezek szerint a terület:

(36 - 18) \cdot π = 18 π

6. Miskolcon a Tiszai pályaudvar várótermének kövezéséhez az ábrán látható burkolólapokat is használtak. Ezeken a lapokon egy ötször ötös négyzethálót színeztek három színnel (sötétzöld, világoszöld, fehér).
Ezt a mintát jobbra és felfelé tovább folytathatjuk, és bármely ötnél nagyobb páratlan számhoz elkészíthetjük az ábra színezését. Lerajzoltuk az így készített hétszer hetes négyzethálót is.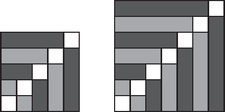

a)

Hányadrésze lesz világoszöld az

51

egység oldalú négyzetnek?

b)

Hányadrésze lesz sötétzöld a

101

egység oldalú négyzetnek?

c)

Igazoljuk, hogyha a négyzet oldalhosszát minden határon túl növeljük, akkor mind a világoszöld, mind a sötétzöld részek területe a négyzet területének a feléhez tart. (16 pont)

Megoldás.

a)

Az 51 egység oldalú négyzet

51^{2}

, azaz 2601 területű. A világoszöld téglalapok területe sorban:

1,3,5,7, ...,49

. Mindegyikből kettő van, ezért területük összege:

2 (1 + 3 + 5 + ... + 49) = 2 \cdot 25^{2} = 1250

. (Felhasználtuk, hogy az első 25 pozitív páratlan szám összege

25^{2}

.)
Vagyis az

\frac{1250}{2601} \approx 0, 480 58

része lesz világoszöld az 51 egység oldalú négyzetnek.

b)

A 101 egység oldalú négyzet

101^{2}

, azaz 10 201 területű. A sötétzöld téglalapok területe sorban:

2,4,6,8, ...,100

. Mindegyikből kettő van, ezért területük összege:

\begin{matrix} 2 (2 + 4 + 6 + ... + 100) = 4 (1 + 2 + 3 + ... + 50) = 4 \cdot \frac{50 \cdot 51}{2} = 5100. \end{matrix}

Vagyis az

\frac{5100}{10201} \approx 0, 499 95

része lesz sötétzöld a 101 egység oldalú négyzetnek.

c)

2 n + 1

egység oldalú négyzet

{(2 n + 1)}^{2}

területű, ahol

n

tetszőleges 1-nél nagyobb pozitív egész számot jelöl. A világoszöld téglalapok területe sorban:

1,3, ..., (2 n - 1)

. Mindegyikből kettő van, ezért területük összege:

\begin{matrix} 2 \cdot [1 + 3 + 5 + ... + (2 n - 1)] = 2 \cdot n^{2} . \end{matrix}

A következő értéket kell meghatároznunk:

\begin{matrix} {lim}_{n \to \infty}^{} \frac{2 n^{2}}{{(2 n + 1)}^{2}} . \end{matrix}

Végezzük el a kijelölt műveleteket és alkalmazzuk a határértékre megismert tulajdonságokat:

\begin{matrix} {lim}_{n \to \infty}^{} \frac{2 n^{2}}{{(2 n + 1)}^{2}} = {lim}_{n \to \infty}^{} \frac{2 n^{2}}{4 n^{2} + 4 n + 1} = {lim}_{n \to \infty}^{} \frac{2}{4 + \frac{4}{n} + \frac{1}{n^{2}}} = 0, 5. \end{matrix}

A sötétzöld téglalapok területe sorban:

2,4,6, ...,2 n

. Mindegyikből kettő van, ezért területük összege:

\begin{matrix} 2 (2 + 4 + ... + 2 n) = 4 (1 + 2 + ... + n) = 4 \cdot \frac{n \cdot (n + 1)}{2} = 2 n (n + 1) . \end{matrix}

Most a következő értéket kell meghatároznunk:

\begin{matrix} {lim}_{n \to \infty}^{} \frac{2 n (n + 1)}{{(2 n + 1)}^{2}} . \end{matrix}

Végezzük el a kijelölt műveleteket és alkalmazzuk a határértékre megismert tulajdonságokat:

\begin{matrix} {lim}_{n \to \infty}^{} \frac{2 n (n + 1)}{{(2 n + 1)}^{2}} = {lim}_{n \to \infty}^{} \frac{2 n^{2} + 2 n}{4 n^{2} + 4 n + 1} = {lim}_{n \to \infty}^{} \frac{2 + \frac{2}{n}}{4 + \frac{4}{n} + \frac{1}{n^{2}}} = 0, 5. \end{matrix}

Ezzel mindkét esetben igazoltuk az állítást.

7. A

[0; 4]

-on értelmezett

f (x) = \frac{x^{2}}{16} + 1

hozzárendeléssel adott függvény képét megforgatjuk az

x

tengely körül. Az így kapott felület egy olyan forgástest alakú edény palástját adja, melynek az alja a kisebb kör. A koordinátarendszer egysége a valóságban 1 dm-t jelent.

a)

Hány literes az edény, ha falvastagságát elhanyagolhatónak vehetjük?

b)

Az edény aljának középpontjában áll egy elhanyagolható vastagságú egyenes pálca. Ezt a pálcát úgy döntjük el, hogy az alsó vége nem mozdul el. Milyen magasságban érinti a pálca az edény falát? (16 pont)

Megoldás.

a)

[0; 4]

-on értelmezett

f (x) = \frac{x^{2}}{16} + 1

hozzárendeléssel adott függvény forgatásával kapott forgástest térfogata (1. ábra):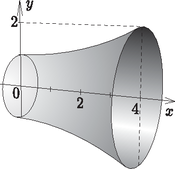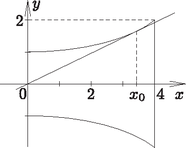

\begin{matrix} V & = π \int_{0}^{4} {(\frac{x^{2}}{16} + 1)}^{2} d x = π \int_{0}^{4} (\frac{x^{4}}{256} + \frac{x^{2}}{8} + 1) d x = π {[\frac{x^{5}}{1280} + \frac{x^{3}}{24} + x]}_{0}^{4} = \\ = π (\frac{4^{5}}{1280} + \frac{4^{3}}{24} + 4 - \frac{0^{5}}{1280} - \frac{0^{3}}{24} - 0) = \frac{52 π}{15} \approx 23, 5. \end{matrix}

Az edény kb. 23,5 literes.

1. ábra

2. ábra

b)

A rajz a forgástengelyre illeszkedő keresztmetszetet mutatja az eldöntött pálcával (2. ábra). A kérdéses magasság legyen

x_{0}

.
Írjuk fel az origóból az

f

függvényhez húzható érintő egyenletét. Az origóra illeszkedő egyenesek egyenlete:

y = m x

(most

m > 0

), az

f

függvény görbéjének
egyenlete:

y = \frac{x^{2}}{16} + 1

.
A behelyettesítés után kapjuk:

m x = \frac{x^{2}}{16} + 1

\begin{matrix} 0 = x^{2} - 16 m x + 16, D = 256 m^{2} - 64 = 0. \end{matrix}

Minden feltételnek az

m = \frac{1}{2}

felel meg, vagyis a keresett érintő egyenlete:

y = \frac{x}{2}

. Ez az érintő a

(4; 2)

koordinátájú pontban érinti az

f

függvény képét.
Vagyis

x_{0} = 4

. (Ez az edény felső peremének magassága.)

8. Oldjuk meg a

- x^{2} + 12 x - 33 = \sqrt[]{x - 3} + \sqrt[]{x - 7}

egyenletet. (16 pont)
Megoldás. A feladat értelmezési tartománya:

x \geq 7

. Alakítsuk át a bal oldalon látható másodfokú kifejezést: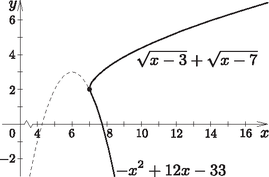

\begin{matrix} - x^{2} + 12 x - 33 = - (x^{2} - 12 x + 33) = - [{(x - 6)}^{2} - 3] = - {(x - 6)}^{2} + 3. \end{matrix}

Ebben az alakban már könnyen megállapítható, hogy az

x = 6

maximum helye ennek a kifejezésnek, és a

[6; \infty]

-on szigorúan monoton csökkenő, vagyis a feladat értelmezési tartományán is az.
Mivel a

\sqrt[]{x - 3}

és a

\sqrt[]{x - 7}

szigorúan monoton növekedő, azért az összegük is az. Az értelmezési tartomány legkisebb elemére, az

x = 7

-re a bal oldal helyettesítési értéke:

\begin{matrix} - x^{2} + 12 x - 33 = - 7^{2} + 12 \cdot 7 - 33 = 2, \end{matrix}

a jobb oldal helyettesítési értéke:

\begin{matrix} \sqrt[]{x - 3} + \sqrt[]{x - 7} = \sqrt[]{7 - 3} + \sqrt[]{7 - 7} = 2. \end{matrix}

Az egyenlőség miatt az

x = 7

megoldása az egyenletnek. Több megoldás a fent elmondottak miatt nincs.

9. Egy háromszögben ismerjük mindhárom oldal hosszát és mindhárom szög nagyságát. Mutassuk meg, hogy ezeket az értékeket az

\begin{matrix} \frac{{(\frac{a}{2})}^{2} + {(\frac{b}{2})}^{2} + {(\frac{c}{2})}^{2}}{ctg α + ctg β + ctg γ} \end{matrix}

képletbe behelyettesítve a háromszög területét kapjuk. (16 pont)

Megoldás. A megadott képletet alakítsuk a következő módon:

\begin{matrix} \frac{{(\frac{a}{2})}^{2} + {(\frac{b}{2})}^{2} + {(\frac{c}{2})}^{2}}{ctg α + ctg β + ctg γ} = \frac{a^{2} + b^{2} + c^{2}}{4 \cdot (\frac{cos α}{sin α} + \frac{cos β}{sin β} + \frac{cos γ}{sin γ})} . \end{matrix}

A koszinusz-tételt alkalmazva:

cos α = \frac{b^{2} + c^{2} - a^{2}}{2 b c}

. Ugyanígy felírhatjuk

cos β

és

cos γ

értékét is:

\begin{matrix} cos β = \frac{a^{2} + c^{2} - b^{2}}{2 a c}, cos γ = \frac{a^{2} + b^{2} - c^{2}}{2 a b} . \end{matrix}

Vagyis:

\begin{matrix} \frac{a^{2} + b^{2} + c^{2}}{4 \cdot (\frac{cos α}{sin α} + \frac{cos β}{sin β} + \frac{cos γ}{sin γ})} = \frac{a^{2} + b^{2} + c^{2}}{4 \cdot (\frac{\frac{b^{2} + c^{2} - a^{2}}{2 b c}}{sin α} + \frac{\frac{a^{2} + c^{2} - b^{2}}{2 a c}}{sin β} + \frac{\frac{a^{2} + b^{2} - c^{2}}{2 a b}}{sin γ})} = \\ = \frac{a^{2} + b^{2} + c^{2}}{4 \cdot (\frac{b^{2} + c^{2} - a^{2}}{2 b c sin α} + \frac{a^{2} + c^{2} - b^{2}}{2 a c sin β} + \frac{a^{2} + b^{2} - c^{2}}{2 a b sin γ})} = \frac{a^{2} + b^{2} + c^{2}}{4 \cdot (\frac{b^{2} + c^{2} - a^{2}}{4 t} + \frac{a^{2} + c^{2} - b^{2}}{4 t} + \frac{a^{2} + b^{2} - c^{2}}{4 t})} = \\ = \frac{t (a^{2} + b^{2} + c^{2})}{(b^{2} + c^{2} - a^{2}) + (a^{2} + c^{2} - b^{2}) + (a^{2} + b^{2} - c^{2})} = \frac{t (a^{2} + b^{2} + c^{2})}{a^{2} + b^{2} + c^{2}} = t . \end{matrix}

Valóban a háromszög területét adja ez a képlet.