Cím:	A 2010‐2011. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2011/november, 450 - 456. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A 2010‐2011. évi Arany Dániel Matematikai Tanulóverseny feladatai   KEZDŐK   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. András, Béla, Csaba, Dénes és Elemér egy asztal körül ülnek. Andrásnál kezdetben 5 kavics van, a többieknél egy sincs. Egy lépés abból áll, hogy valaki, akinél legalább 2 kavics van, a két szomszédjának ad egyet-egyet. El tudják-e érni, hogy néhány lépés után mindannyiuknál pontosan 1 kavics legyen?   2. Egy 4-fős társaság a következő játékot játszotta. Egy zsákba betettek 3 piros és 3 kék sapkát, majd mindenki behunyt szemmel kihúzott egy sapkát és a fejére tette. Ezek után kinyitották a szemüket, és megvizsgálták egymás sapkáinak a színét. A következő beszélgetés játszódott le közöttük: A: ,,Nem tudom, hogy milyen színű sapka van a fejemen.'' B: ,,Mielőtt ezt mondtad én is így voltam vele, de most már kitaláltam, hogy az én fejemen milyen színű sapka van.'' Milyen színű sapkák maradtak a zsákban?   3. Hány olyan hatjegyű természetes szám van, amelynek 2011-gyel való osztási maradéka 2010?   4. Az $ABCDEF$ hatszögre igaz, hogy minden szöge ${120}^{\circ }$-os, $AB$ oldala 2 cm, $BC$ oldala 7 cm, $CD$ oldala 3 cm és $DE$ oldala 4 cm hosszú. Milyen hosszúak az $EF$, illetve $FA$ oldalak?   Második forduló   1. Hány olyan 3-mal osztható hatjegyű természetes szám van (a tízes számrendszerben), amelyben nincs 2-nél nagyobb számjegy?   2. Az első tíz pozitív egész szám közül kiválasztottunk hatot. Bizonyítsa be, hogy van olyan 1-nél nagyobb négyzetszám, amely osztója a szorzatuknak!   3. Jelölje $\text{P}$ a prímszámok halmazát! Legyen $f:\text{P}\to \text{R}$ $x\mapsto \left\{\frac{x^2-1}{24}\right\}$, ahol $\left\{z\right\}$ a $z$ szám törtrészét jelöli (azaz $\left\{z\right\}=z-\left[z\right]$ és $\left[z\right]$ a $z$ egész része, vagyis az a legnagyobb egész szám, amely $z$-nél nem nagyobb)! Mi az $f$ függvény értékkészlete?   4. Van-e olyan $x$ egész szám, amelyre: $\begin{array}{c}{\displaystyle 2010+2009x+2008x^2+2007x^3+\text{...}+3x^{2007}+2x^{2008}+x^{2009}=0?}\end{array}$   5. Legalább mekkora egy olyan trapéznak a kerülete, amelynek alapjai 10 cm és 20 cm, magassága 12 cm?   Harmadik (döntő) forduló   1. Rajzoljon egy 3 egység sugarú körbe egy 1 és egy 2 egység sugarú kört, amelyek egymást kívülről, a nagy kört pedig belülről érintik! Határozza meg annak a körnek a sugarát, amely a nagy kört belülről, a két kisebb kört pedig kívülről érinti!   2. Négy házaspár moziba megy. Sikerül egymás mellé kapniuk 8 jegyet. Hányféleképpen ülhetnek le a nyolc helyre, ha sem azonos neműek, sem pedig házastársak nem szeretnének egymás mellé ülni?   3. Az $x$, $y$ és $z$ valós számokra teljesülnek a következő egyenlőségek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x+y+z}& {\displaystyle =\mathrm{1,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle x^3+y^3+z^3}& {\displaystyle =\mathrm{91,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle x^5+y^5+z^5}& {\displaystyle =4651.}\hfill \end{array}}$ Mekkora lehet $x$, $y$ és $z$?   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló Megegyezik az I. kategória első fordulós feladatsorával.   Második forduló Megegyezik az I. kategória második fordulós feladatsorával.   Harmadik (döntő) forduló   1. Az $A$, $B$, $C$ szabályos háromszög körülírt körének sugara 1. Legyen a körülírt kör egy $P$ pontjának az $A$, $B$, $C$ csúcsokról mért távolsága rendre $a$, $b$ és $c$! Határozza meg $abc$ maximumát, ha $P$ befutja a körülírt kört!   2. Az $x$, $y$ és $z$ valós számokra teljesülnek a következő egyenlőségek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x+y+z}& {\displaystyle =\mathrm{1,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle x^3+y^3+z^3}& {\displaystyle =\mathrm{91,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle x^5+y^5+z^5}& {\displaystyle =4651.}\hfill \end{array}}$ Mekkora lehet $x$, $y$ és $z$?   3. Van-e 14 olyan, egymás után következő pozitív egész szám, hogy a számok mindegyike osztható a 2; 3; 5; 7; 11 prímek közül legalább eggyel?   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló Megegyezik az I. kategória második fordulós feladatsorával.   Második (döntő) forduló   1. Az $x$, $y$ és $z$ valós számokra teljesülnek a következő egyenlőségek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x+y+z}& {\displaystyle =\mathrm{1,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle x^3+y^3+z^3}& {\displaystyle =\mathrm{91,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle x^5+y^5+z^5}& {\displaystyle =4651.}\hfill \end{array}}$ Mekkora lehet $x$, $y$ és $z$?   2. Tekintse a legkisebb 20 db pozitív egész számot és sorolja őket tetszőlegesen két 10-elemű csoportba! Képezze az összes olyan 2-tényezős szorzatot, melyek tényezői különböző csoportból valók! Bizonyítsa be, hogy mindig lesz két olyan szorzat, melyek között pontosan 2 a különbség!   3. Az $ABC$ egységoldalú szabályos háromszög $B$, illetve $C$ csúcsához tartozó magasságvonalak $m_b$, illetve $m_c$. Legyen $e$ egy olyan egyenes, mely az $A$ csúcson áthalad, metszi a $BC$ oldalszakaszt és az $AC$ oldallal ${10}^{\circ }$-os szöget zár be, továbbá legyen $e$ és $m_b$ metszéspontja $X$, $e$ és $m_c$ metszéspontja $Y$! Jelölje az $AX$ szakasz hosszát $x$, míg a $CY$ szakaszét $y$! Számítsa ki a $2y\left(1+x^2\right)+x\left(2+y^2\right)$ pontos értékét!   HALADÓK I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Van 11 érménk, melyek értéke rendre: 7, 300, 35, 83, 1, 17, 2, 1, 17, 170 és 5 fabatka. Melyik az a legkisebb pozitív egész összeg, ami visszaadás nélkül nem fizethető ki ezekkel az érmékkel?   2. Egy téglalap egyik oldala a másik ötszöröse. A téglalap szögfelezői által meghatározott négyszög területe 32 cm${}^2$. Mekkora a téglalap területe?   3. Bizonyítsuk be, hogy ha $a$, $b$, $c$ olyan természetes számok, hogy $9-d{a}^3+b^3+c^3$, akkor az $a$, $b$, és $c$ közül valamelyik osztható 3-mal.   4. Egy egyenlőszárú háromszög valamelyik súlyvonalának hossza megegyezik az egyik középvonal hosszával. Mekkora lehet a háromszög legnagyobb szöge?   5. Tudjuk, hogy az $x^2-px+4^{10}=0$ egyenletnek két különböző gyöke van, amelyek pozitív egész páros számok. Hányféle különböző értékű lehet a $p$ paraméter?   Második forduló   1. Egy adott négyzet mindegyik oldalán kijelöltünk a csúcsoktól különböző 3‐3 darab pontot. Összesen hány konvex négyszöget határoz meg a felvett 12 darab pont?   2. Határozzuk meg azokat a $p$ prímeket, melyekre a $p^2+11$ számnak pontosan 6 db pozitív osztója van!   3. Bizonyítsa be, hogy ha $2^n$-nek a tízes számrendszerbeli alakjából levágjuk az utolsó számjegyet és ezzel megszorozzuk az előtte álló jegyekből alakuló számot, akkor a szorzat osztható 6-tal ($n>3$)!   4. Az $ABCD$ négyzet $BC$, illetve $CD$ oldalán úgy vettük fel az $E$ és $F$ pontot, hogy $BE+DF=AE$. Bizonyítsuk be, hogy ekkor $AF$ felezi az $EAD$ szöget.   Harmadik (döntő) forduló   1. Bizonyítsuk be, hogy nincs megoldása az $x^2+y^3=z^4$ egyenletnek, ha $x$, $y$ és $z$ pozitív prímek!   2. Bizonyítsuk be, hogy ha egy derékszögű trapéz átlói merőlegesek egymásra, akkor a trapéz területe nem lehet nagyobb az oldalak négyzetének számtani közepénél.   3. Három gép olyan számkártyákkal működik, amelyeken pozitív egészekből álló rendezett számpárok találhatók. Mindhárom gép új számkártyák kinyomtatására képes, a következő szabályok szerint: $•$ Az első gépbe az $\left(a\mathrm{,}b\right)$ kártyát táplálva az $\left(a+\mathrm{1,}b+1\right)$ kártyát nyomtatja ki. $•$ A második gép az $\left(a\mathrm{,}b\right)$ kártya beadására az $\left(\frac{a}{2}\mathrm{,}\frac{b}{2}\right)$ kártyát adja ki, de csak akkor, ha $a$ és $b$ páros. Más esetekben nem nyomtat. $•$ A harmadik gépbe két kártyát kell betölteni: az $\left(a\mathrm{,}b\right)$ és $\left(b\mathrm{,}c\right)$ kártyák betöltése esetén az $\left(a\mathrm{,}c\right)$ kártyát nyomtatja ki. Csak akkor nyomtat, ha két olyan kártyát adunk be (megfelelő sorrendben), hogy az első kártya második száma egyenlő a második kártya első számával. Mindhárom gép visszaadja a betáplált kártyákat is, függetlenül attól, hogy történt-e nyomtatás. Kezdetben egyetlen kártyánk van, az $\left(\mathrm{1,}27\right)$. Legyártható-e $a)$ az $\left(\mathrm{1,}2011\right)$; $b)$ a $\left(\mathrm{99,}333\right)$ kártya?   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   1. Melyek azok a természetes számokból álló $\left(x;y\right)$ számpárok, amelyekre teljesül, hogy $\begin{array}{c}{\displaystyle \frac{x^y\cdot x^{2y}\cdot \sqrt[]{x^{3y}}}{x^{4y}}={\left(\sqrt[]{2}\right)}^y\text{és}x+y=2010?}\end{array}$   2. Hány olyan 2-es számrendszerben felírt 12-jegyű 2-es számrendszerbeli pozitív egész szám van, amelyekben nincs két darab szomszédos 1-es számjegy?   3. Legfeljebb hány darab 0 számjegyre végződhet a tízes számrendszerben az $\begin{array}{c}{\displaystyle 1^n+2^n+3^n+4^n}\end{array}$ összeg, ahol $n$ tetszőleges pozitív egész szám?   4. Az $AB$ alapú $ABC$ egyenlő szárú háromszög $BC$ oldalának felezőpontja $P$, $AC$ oldalának felezőpontja $Q$. Az $A$ csúcsból húzott belső szögfelező a $BC$ oldalt a $D$ pontban, míg a $PQ$ szakaszt a szakasz $H$ harmadolópontjában metszi. Hányadrésze a $HPD$ háromszög területe az $ABC$ háromszög területének?   5. Artúr király testőrei lovagi tornát vívtak. A torna végén kiderült, hogy a király bármely két testőréhez tud találni egy harmadikat, aki mindkettőjüket legyőzte. Legalább hány testőr vett részt a tornán? (Két lovag legfeljebb egyszer vívott egymással.)   Második forduló   1. Egy sportversenyen 15 csapat vett részt, és minden csapat minden csapattal egyszer mérkőzött. A győzelemért 3, a döntetlenért 2, a vereségért 1 pont járt. A verseny végén minden csapatnak más volt a pontszáma, az utolsó 21 pontot szerzett. Bizonyítsuk be, hogy a legtöbb pontot gyűjtött csapat legalább egyszer döntetlenül mérkőzött!   2. 2. 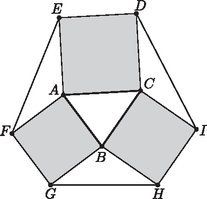Az $ABC$ háromszög oldalaira kifelé négyzeteket írunk. A négyzetek területe 18, 20 és 26 egység. Ezután összekötjük az ábra szerint a négyzetek ,,külső'' csúcsait. Mekkora az így keletkezett $DEFGHI$ hatszög területe?     3. Mekkora a területe annak a sokszögnek, amelyet az alábbi egyenletrendszer gyökei határoznak meg a derékszögű koordináta-rendszerben? $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle xy+x+y}& {\displaystyle =11}\hfill \\ \multicolumn{2}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle x^{2}y+x{y}^2}& {\displaystyle =30}\hfill \end{array}}\}}\end{array}$   4. A valós számok halmazán értelmezett $f\left(x\right)=a{x}^2+bx+c$ másodfokú függvénynek minimuma van, melynek értéke $-a$. Az $f\left(x\right)$ függvényre bármely $x$ érték esetén $f\left(x\right)=f\left(1-x\right)$ teljesül. Adjuk meg az $f\left(x\right)$ függvény zérushelyeit!   Harmadik (döntő) forduló   1. Állítsuk elő tetszőleges $n$ pozitív egész szám esetén a $36n^2+25+12n$ összeget minimális számú páratlan négyzetszám összegeként!   2. Az $ABCD$ derékszögű trapéz alapjai $AB=a$, $CD=c$ hosszúak, a derékszögű szár $AD=d$, a másik szár $BC=b$ hosszú. A trapéz átlói merőlegesek egymásra. Bizonyítsuk be, hogy az $a$, $b$, $c$, $d$ oldalakból ‐ mint szakaszokból ‐ kiválasztható három úgy, hogy a kiválasztott oldalakból szerkeszthető háromszögnek biztosan lesz ${60}^{\circ }$-os szöge.   3. Adottak az $\left\{1\right\}$, $\left\{1;2\right\}$, $\left\{1;2;3\right\}$, $\left\{1;2;3;4\right\}$, $\text{...}$, $\left\{1;2;3;\text{...};8\right\}$ halmazok. A halmazok mindegyikéből kiválasztunk egy-egy elemet. Egy $k$ elemű halmazból egy elemet $\frac{1}{k}$ valószínűséggel választunk. $p_k$-val jelöljük annak valószínűségét, hogy a kiválasztott 8 darab szám maximuma éppen $k$. Határozzuk meg a $p_1\mathrm{,}{p}_2\mathrm{,}{p}_3\mathrm{,}\text{...}\mathrm{,}{p}_8$ valószínűségek legnagyobb értékét!   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   1. Határozzuk meg az $n$ és az $A$ természetes számot úgy, hogy az $A=2n^3+10n^2-2n-10$ számnak pontosan 8 osztója legyen!   2. Milyen $x$ valós szám esetén lesz legkisebb a $\sqrt[]{x^2+9}+\sqrt[]{x^2-20x+101}$ kifejezés értéke?   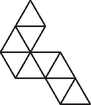3. Egy szabályos háromszög oldalait $n$ egyenlő részre bontottuk. Az osztópontokon keresztül párhuzamosokat rajzoltunk a háromszög oldalaival, így az eredeti háromszöget kisebb szabályos háromszögekre daraboltuk. Nevezzük kígyónak a kis szabályos háromszögek olyan sorozatát, amelyben az egymást követő elemeknek van közös oldala. Például $n=4$-re így nézhet ki egy kígyó: Mekkora a lehetséges leghosszabb kígyó? 4. 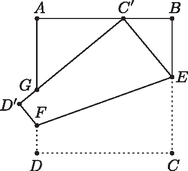Egy $ABCD$ négyzet alakú papírt félbehajtunk úgy, hogy a $C$ csúcs az $AB$ oldalon fekvő $C\text{'}$ pontba kerül.     $a)$ Bizonyítsuk be, hogy a $C$ középpontú és $CB$ sugarú kör érinti a $C\text{'}D\text{'}$ egyenest! $b)$ Bizonyítsuk be, hogy a $C\text{'}BE$ és $FGD\text{'}$ háromszögek kerületének összege egyenlő az $AC\text{'}G$ háromszög kerületével!   5. Végtelen sok olyan háromszög van, amelynek oldalai (1) páronként különböző egész számok, továbbá (2) a háromszög egyik szöge ${60}^{\circ }$. Például az 5, 7, 8 egység oldalú háromszög megfelelő. Kérdésünk az, hogy az (1) és (2) feltételek teljesülése esetén lehet-e mindegyik oldal értéke prímszám?   Második (döntő) forduló   1. Bizonyítsuk be, hogy a koordinátarendszer kezdőpontja, valamint a valós számok lehető legbővebb halmazán értelmezett $f\left(x\right)=x^2-4x$ és $g\left(x\right)=2+\sqrt[]{x+4}$ függvények grafikonjának metszéspontjai olyan konvex sokszöget határoznak meg, melynek egyik szöge derékszög.   2. Az $A_1{A}_2{A}_3{A}_4$ húrnégyszögben bevezetjük a ciklikus indexelést: $A_i$ és $A_{i+4}$ jelentse ugyanazt a csúcsot. Az $A_i$ pont merőleges vetülete az $A_{i+1}{A}_{i+2}$ egyenesen legyen $P_i$, az $A_{i+1}{A}_{i+3}$ egyenesen pedig $Q_i$. Bizonyítsuk be, hogy a $P_i{Q}_i$ egyenesek ($i=\mathrm{1,2,3,4}$) egy ponton mennek át.   3. A Zenekedvelők Végtelen Kollégiumában egyetlen ‐ mindkét irányban végtelen hosszú ‐ folyosón vannak a lakószobák, egészekkel sorszámozva. Lehetnek üres szobák, és egy szobában többen is lakhatnak. Minden szobában áll egy hatalmas zongora, amin a lakók szeretnek játszani. Ha azonban két szomszéd (a $k$. és a $\left(k+1\right)$. szobában) gyakorol a zongorán, az kellemetlen zenei élményhez vezet, ezért egy szobával arrébb költöznek. Ez minden nap a következő módon történik: ha vannak szomszédok, akkor kiválasztunk egy-egy szomszédos lakót (a $k$. és a $\left(k+1\right)$. szobában), és egyikőjük a $\left(k-1\right)$., a másik pedig a $\left(k+2\right)$. szobába költözik. Bizonyítsuk be, hogy ha a kollégiumnak véges sok lakója van, akkor véges sok nap után abbamarad a költözködés.