Cím:	Megoldásvázlatok a 2011/6. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2011/október, 397 - 403. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Egy téglalap oldalainak aránya $1:2$. Tudjuk, hogy a terület mérőszáma egyenlő a kerület és az átlók hosszának összegét jelölő mérőszámmal. Határozzuk meg a téglalap egy csúcsának távolságát a csúcsot nem tartalmazó átlótól.  (11 pont)   Megoldás. A téglalap oldalai: $a$, $2a$, ekkor átlójának hossza: $a\sqrt[]{5}$. A téglalap területe: $2a^2$, a kerületének és az átlók hosszának összege: $2a\left(3+\sqrt[]{5}\right)$. Tudjuk, hogy $2a^2=2a\left(3+\sqrt[]{5}\right)$. Mivel $a=0$ nem lehet, így $a=3+\sqrt[]{5}$. A téglalap területét az átló, valamint egy csúcs és annak az átlótól való $m$ távolsága segítségével is kiszámíthatjuk: $2\cdot \frac{a\sqrt[]{5}\cdot m}{2}$. A kétféle módon felírt terület egyenlőségéből és az $a$ kiszámolt értékéből kapjuk: $\left(3+\sqrt[]{5}\right)\sqrt[]{5}\cdot m=2{\left(3+\sqrt[]{5}\right)}^2$. Ebből kifejezhető $m$ értéke: $\begin{array}{c}{\displaystyle m=\frac{2\left(3+\sqrt[]{5}\right)}{\sqrt[]{5}}=\frac{6\sqrt[]{5}+10}{5}\mathrm{.}}\end{array}$   2. Oldjuk meg a következő egyenletrendszert: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2-y^2-8x+8y}& {\displaystyle =\mathrm{0,}}\hfill \\ \multicolumn{2}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle xy-3x-y}& {\displaystyle =0.}\hfill \end{array}}\}}\end{array}$ (12 pont)   Megoldás. Az első egyenletet írjuk szorzatalakban: $\left(x-y\right)\left(x+y-8\right)=0$. Ebből következik, hogy $y=x$ vagy $y=-x+8$. Mindkét esetben a második egyenletbe behelyettesítve $x$-re másodfokú egyenletet kapunk. Az első esetben: $x^2-4x=0$. Ekkor két megoldást kapunk:  ${\displaystyle \begin{array}{cc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>0</mn></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>0</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>. }}\hfill \end{array}}$ A második esetben: $x^2-6x+8=0$. Ebben az esetben is két megoldást kapunk, de az egyik már az előzőekben szerepelt:  ${\displaystyle \begin{array}{cc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>2</mn></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>6</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mn>4</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mn>4</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>. }}\hfill \end{array}}$ Vagyis az egyenletrendszernek három megoldása van.   3. A térkövezéshez nagyon sokféle alakú és színű kő vásárolható. Az ábrákon az úgynevezett fodorkövet, és az ebből kialakítható mintasorozatot látjuk.     $a)$ Hány darab sötétszürke kő szükséges a hatodik mintához? $b)$ Hányadik mintához kell pontosan $150$ darab sötétszürke kő? $c)$ Adjuk meg rekurzív képlettel a sötétszürke kövek számát az $n$-edik mintában.  (14 pont)     Megoldás. $a)$ Az ábrasorozat tanulmányozásával látható, hogy a hatodik minta a negyedikből származtatható. Egy világos sáv kirakása után minden oldalon hat-hat sötétszürke követ kell leraknunk, de ekkor a sarkokat kétszer számoltuk. Mivel a negyedik minta 24 sötétszürke követ tartalmaz, ezért a hatodikhoz $24+6\cdot 6-6$, azaz 54 darab sötétszürke kő kell. $b)$ Az előző gondolatot alkalmazva a sorozat egymást követő tagjai a következő módon alakulnak: $\mathrm{1,6,13,24,37,54,73,96,121,150,}\text{...}\mathrm{.}$ Vagyis a sorozat 10. tagja a 150. $c)$ Tudjuk, hogy $a_1=1$, $a_2=6$. Az $n$-edik ábrán (ahol $n>2$ és egész szám) a sötétszürke kövek száma: $a_n=a_{n-2}+6\cdot n-6$.   4. Egy iskolai sakkbajnokságon mindenki pontosan egyszer játszott mindenkivel. $63$ játszma után még mindenkinek négy játszmája hátravolt. $a)$ Hányan szerepeltek összesen a bajnokságon? $b)$ Ekkor két véletlenszerűen kiválasztott játékossal beszélgetett az iskolaújság egyik szerkesztője. Mekkora a valószínűsége, hogy ők még nem játszottak egymással?  (14 pont)   Megoldás. $a)$ Legyen a csapatok száma $n$, ekkor az összes játszmák száma: $\frac{n\left(n-1\right)}{2}$. Mindenkinek négy játszmája volt még hátra, vagyis $\frac{4n}{2}$ játszmát kell még lejátszani. A lejátszott mérkőzések száma: $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)}{2}-\frac{4n}{2}=\mathrm{63,}}\end{array}$ amiből az $n^2-5n-126=0$ másodfokú egyenletet kapjuk. Az egyenlet gyökei: $n_1=14$, $n_2=-9$. Vagyis a sakkbajnokságon 14-en szerepeltek. $b)$ Az összes játszmák száma: $\frac{14\cdot 13}{2}=91$. A kedvező esetek száma: $91-63=28$. A keresett valószínűség: $\begin{array}{c}{\displaystyle \frac{28}{91}=\frac{4}{13}\approx 0\mathrm{,}31.}\end{array}$   II. rész   5. $a)$ Ha $2$-vel csökkentjük az $a{x}^2+bx+c=0$ egyenlet gyökeit, akkor az $a{x}^2+cx+b=0$ egyenlet gyökeit kapjuk. Adjuk meg az eredeti egyenlet együtthatóit, ha tudjuk, hogy az összegük $-3$. $b)$ Az $a{x}^2+bx+c=0$ egyenletben az együtthatók egy növekedő számtani sorozat három egymást követő tagjai, az $\begin{array}{c}{\displaystyle \left(a+2\right)x^2+bx+\left(c+2\right)=0}\end{array}$ egyenletben az együtthatók pedig egy mértani sorozat három egymást követő tagjai. Van-e valós megoldása az első egyenletnek, ha az együtthatóinak összege 9? $c)$ Az $a{x}^2+bx+c=0$ másodfokú egyenlet két zérushelye $x_1$ és $x_2$. Írjunk fel egy olyan harmadfokú egyenletet gyöktényezős alakban, amelynek zérushelyei: $x_1{x}_2$; $x_1^2+x_2^2$; $\frac{1}{x_1}+\frac{1}{x_2}$.  (16 pont)   Megoldás. $a)$ A második egyenlet gyökei: $x_1$ és $x_2$, ez alapján: $x_1+x_2=-\frac{c}{a}$, $x_1{x}_2=\frac{b}{a}$. Ekkor $x_1+2+x_2+2=-\frac{c}{a}+4=-\frac{b}{a}$, valamint $\begin{array}{c}{\displaystyle \left(x_1+2\right)\left(x_2+2\right)=x_1{x}_2+2\left(x_1+x_2\right)+4=\frac{b}{a}+2\cdot \left(-\frac{c}{a}\right)+4=\frac{c}{a}\mathrm{.}}\end{array}$ Vagyis a következő egyenletrendszert kell megoldanunk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a+b+c}& {\displaystyle =-\mathrm{3,}}\hfill \\ \hfill {\displaystyle 4a+b-c}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle 4a+b-3c}& {\displaystyle =0.}\hfill \end{array}}\}}\end{array}$ A megoldás: $a=1$, $b=-4$, $c=0$. $b)$ A feladat szövege szerint most a következő egyenletrendszert kapjuk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle 2b=a+c\mathrm{,}}\\ \hfill {\displaystyle b^2=\left(a+2\right)\left(c+2\right)\mathrm{,}}\\ \hfill {\displaystyle a+b+c=9.}\end{array}}\}}\end{array}$ Az első és a harmadik egyenlet összevetésével azonnal kapjuk, hogy $b=3$. Ekkor az első és a második egyenlet a következő egyenletrendszert adja: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a+c}& {\displaystyle =\mathrm{6,}}\hfill \\ \hfill {\displaystyle \left(a+2\right)\left(c+2\right)}& {\displaystyle =9.}\hfill \end{array}}\}}\end{array}$ A $c=6-a$ helyettesítéssel az $a^2-6a-7=0$ egyenletet kapjuk. Ennek csak a $b=3$-nál kisebb megoldása elfogadható, mert az együtthatóknak egy növekedő számtani sorozatot kell alkotni, így $a=-1$. Ezek alapján: $c=7$. Az eredeti egyenlet együtthatóinak ismeretében meghatározzuk a diszkrimináns előjelét: $\begin{array}{c}{\displaystyle D=3^2-4\cdot \left(-1\right)\cdot 7>0.}\end{array}$ Vagyis van valós megoldása az első egyenletnek. $c)$ Mivel $x_1{x}_2=\frac{c}{a}$ és $x_1+x_2=-\frac{b}{a}$, ezért $\begin{array}{c}{\displaystyle x_1^2+x_2^2={\left(x_1+x_2\right)}^2-2x_1{x}_2={\left(-\frac{b}{a}\right)}^2-2\cdot \left(\frac{c}{a}\right)=\frac{b^2-2ac}{a^2}\mathrm{,}}\end{array}$ illetve $\begin{array}{c}{\displaystyle \frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{x_1{x}_2}=\frac{-\frac{b}{a}}{\frac{c}{a}}=-\frac{b}{c}\mathrm{.}}\end{array}$ A következő harmadfokú egyenlet megfelel a feladat feltételeinek: $\begin{array}{c}{\displaystyle \left(x-x_1{x}_2\right)\left(x-x_1^2-x_2^2\right)\left(x-\frac{1}{x_1}-\frac{1}{x_2}\right)=\left(x-\frac{c}{a}\right)\left(x-\frac{b^2-2ac}{a^2}\right)\left(x+\frac{b}{c}\right)=0.}\end{array}$   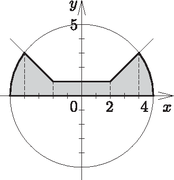6. Az $x^2+y^2=25$ egyenletű kör, az $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{|x+2|+|x-2|-2}{2}}\end{array}$ hozzárendeléssel megadott függvény képe és az abszcisszatengely egy síkidomot határoznak meg, amit az abszcisszatengely körül megforgatunk. Mekkora az így kapott forgástest térfogata?  (16 pont)   Megoldás. Készítsünk vázlatrajzot. Az origó középpontú 5 sugarú kör megrajzolása után ábrázoljuk az $f\left(x\right)$ függvényt is.     Ha $x\in \left]-\infty ;-2\right]$, akkor $f\left(x\right)=\frac{-\left(x+2\right)-\left(x-2\right)-2}{2}=-x-1$. Ha $x\in \left[-2;2\right]$, akkor $f\left(x\right)=\frac{\left(x+2\right)-\left(x-2\right)-2}{2}=1$. Ha $x\in \left]2;\infty \right]$, akkor $f\left(x\right)=\frac{\left(x+2\right)+\left(x-2\right)-2}{2}=x-1$. Ezeket figyelembe véve kapjuk az ábrát. Az $f\left(x\right)$ függvény és a kör metszéspontjainak koordinátái leolvashatók az ábráról, amiknek a helyességét visszahelyettesítéssel kapjuk: $A\left(4;3\right)$ és $B\left(-4;3\right)$. A keletkezett forgástest térfogata: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V}& {\displaystyle =2\pi \left[\underset{0}{\overset{2}{\int }}1dx+\underset{2}{\overset{4}{\int }}{\left(x-1\right)}^{2}dx+\underset{4}{\overset{5}{\int }}\left(25-x^2\right)dx\right]=}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 6pt"> </div>}}\\ \hfill {\displaystyle }& {\displaystyle =2\pi \left[\underset{0}{\overset{2}{\int }}1dx+\underset{2}{\overset{4}{\int }}\left(x^2-2x+1\right)dx+\underset{4}{\overset{5}{\int }}\left(25-x^2\right)dx\right]=}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 6pt"> </div>}}\\ \hfill {\displaystyle }& {\displaystyle =2\pi {\left[x\right]}_0^2+2\pi {\left[\frac{x^3}{3}-x^2+x\right]}_2^4+2\pi {\left[25x-\frac{x^3}{3}\right]}_4^5=}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 6pt"> </div>}}\\ \hfill {\displaystyle }& {\displaystyle =2\pi \cdot 2+2\pi \left(\frac{64}{3}-16+4-\frac{8}{3}+4-2\right)+2\pi \left(125-\frac{125}{3}-100+\frac{64}{3}\right)=}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 6pt"> </div>}}\\ \hfill {\displaystyle }& {\displaystyle =4\pi +\frac{52}{3}\pi +\frac{28}{3}\pi =\frac{92}{3}\cdot \pi \mathrm{.}}\hfill \end{array}}$   7. $a)$ Igazoljuk, hogy $\sqrt[]{31+8\sqrt[]{15}}+\sqrt[]{31-8\sqrt[]{15}}$ egész szám. $b)$ Oldjuk meg a következő egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle \sqrt[]{{\left(31+8\sqrt[]{15}\right)}^x}+\sqrt[]{{\left(31-8\sqrt[]{15}\right)}^x}=\frac{10}{3}\mathrm{.}}\end{array}$ (16 pont)   Megoldás. $a)$ $\begin{array}{c}{\displaystyle \sqrt[]{31+8\sqrt[]{15}}+\sqrt[]{31-8\sqrt[]{15}}=\sqrt[]{{\left(4+\sqrt[]{15}\right)}^2}+\sqrt[]{{\left(4-\sqrt[]{15}\right)}^2}=4+\sqrt[]{15}+4-\sqrt[]{15}=8.}\end{array}$ Tehát valóban egész szám. $b)$ Alakítsuk az egyenletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{{\left(4+\sqrt[]{15}\right)}^{2x}}+\sqrt[]{{\left(4-\sqrt[]{15}\right)}^{2x}}}& {\displaystyle =\frac{10}{3}\mathrm{,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 6pt"> </div>}}\\ \hfill {\displaystyle {\left(4+\sqrt[]{15}\right)}^x+{\left(4-\sqrt[]{15}\right)}^x}& {\displaystyle =\frac{10}{3}\mathrm{.}}\hfill \end{array}}$ Legyen ${\left(4+\sqrt[]{15}\right)}^x=a$, ekkor ${\left(4-\sqrt[]{15}\right)}^x=\frac{1}{a}$. Ekkor az $a+\frac{1}{a}=\frac{10}{3}$ egyenletet kapjuk, amiből a $3a^2-10a+3=0$ másodfokú egyenlet adódik. A gyökök: $a_1=3$, $a_2=\frac{1}{3}$. A ${\left(4+\sqrt[]{15}\right)}^x=3$ egyenletből: $x_1=\text{log}{}_{4+\sqrt[]{15}}3$. A ${\left(4+\sqrt[]{15}\right)}^x=\frac{1}{3}$ egyenletből: $x_2=\text{log}{}_{4+\sqrt[]{15}}\frac{1}{3}$.   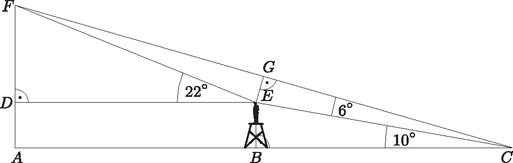8. Egy szabadtéri színpad hátsó részén egy 12 m magas oszlop áll, melynek a súgólyuktól a teteje ${16}^{\circ }$ -os emelkedési szögben látszik. Az oszlop talppontját és a súgólyukat összekötő egyenes fölött van egy emelvény, amelyről a 180 cm magas színész ${22}^{\circ }$ -os emelkedési szögben látja az oszlop tetejét. A súgólyuktól a színész feje búbja ${10}^{\circ }$ -os emelkedési szögű. $a)$ Igazoljuk, hogy a színész feje egyenlő távolságra van az oszlop tetejétől és a súgólyuktól. $b)$ Milyen magas a színpadon felépített emelvény?  (16 pont)   Megoldás. A feladat szövege alapján készítsünk vázlatrajzot.     $a)$ Az ábrán a színpad eleje $C$, az oszlop teteje $F$, az emelvény tetején álló színész fejeteteje $E$. Tudjuk, hogy $AF=12$ m, $ACE\sphericalangle ={10}^{\circ }$, $ACF\sphericalangle ={16}^{\circ }$, $DEF\sphericalangle ={22}^{\circ }$. Az $ACF$ derékszögű háromszögben $FC=\frac{FA}{\text{sin}{16}^{\circ }}$. $ECF\sphericalangle =ACF\sphericalangle -ACE\sphericalangle =6^{\circ }$, $CFE\sphericalangle =CFA\sphericalangle -EFD\sphericalangle ={74}^{\circ }-{68}^{\circ }=6^{\circ }$. Vagyis $EFC$ egyenlőszárú háromszög, valóban $EC=EF$. $b)$ Az $ACF$ derékszögű háromszögben: $CF=\frac{12}{\text{sin}{16}^{\circ }}$. Mivel $EFC$ egyenlőszárú háromszög, azért $G$ a $CF$ felezőpontja, így $GC=\frac{6}{\text{sin}{16}^{\circ }}$. Az $EGC$ derékszögű háromszögben: $\begin{array}{c}{\displaystyle EC=\frac{GC}{\text{cos}{6}^{\circ }}=\frac{\frac{6}{\text{sin}{16}^{\circ }}}{\text{cos}{6}^{\circ }}\mathrm{.}}\end{array}$ Végül az $EBC$ derékszögű háromszögben: $\begin{array}{c}{\displaystyle EB=EC\cdot \text{sin}{10}^{\circ }=\frac{\frac{6}{\text{sin}{16}^{\circ }}}{\text{cos}{6}^{\circ }}\cdot \text{sin}{10}^{\circ }=\frac{6\cdot \text{sin}{10}^{\circ }}{\text{cos}{6}^{\circ }\cdot \text{sin}{16}^{\circ }}\approx 3\mathrm{,}8.}\end{array}$ Mivel a színész testmagassága 1,8 m, azért az emelvény kb. 2 méter magas.   9. $a)$ Egy dobozba $100$ darab piros és zöld építőkockát raktak, méretük alapján kicsiket és nagyokat is. Kis piros kocka véletlenszerű kihúzásának ugyanannyi a valószínűsége, mint annak, hogy nagy pirosat vagy kis zöldet húzunk a dobozból. A zöldek és a kicsik aránya $7:11$. A nagyok $20$ -szal kevesebben vannak, mint a pirosak. Hány kocka van az egyes fajtákból? $b)$ Egy dobozba $93$ darab piros és zöld építőkockát raktak, méretük alapján kicsiket és nagyokat is. Mindegyik fajtából különböző prímszám darab van. A piros kockák száma osztható héttel. A kis zöld kockákból van a legkevesebb. Nagy pirosból ötvennel több van, mint kis pirosból. Hány kocka van az egyes fajtákból?  (16 pont)   Megoldás. $a)$ A következő táblázatból kiolvashatjuk a négy különböző fajta darabszámát jelölő betűket. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|ccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{nagy}}\hfill & \hfill {\displaystyle \text{kicsi }}\hfill \\ \hfill {\displaystyle \text{piros}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math> }}\hfill \\ \hfill {\displaystyle \text{zöld}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi></math> }}\hfill \\ \hline\end{array}}}\end{array}$ A szöveg és a táblázat alapján a következő egyenletrendszer írható fel: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle a+b+c+d=\mathrm{100,}}\\ \hfill {\displaystyle a+d=b\mathrm{,}}\\ \multicolumn{1}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle \frac{c+d}{b+d}=\frac{7}{11}\mathrm{,}}\\ \multicolumn{1}{c}{\text{<div style="line-height: 3pt"> </div>}}\\ \hfill {\displaystyle a+c=a+b-20.}\end{array}}\}}\end{array}$ Az egyenletrendszer megoldása megadja a kérdésre a választ: $a=25$ (nagy piros), $b=40$ (kis piros), $c=20$ (nagy zöld), $d=15$ (kis zöld). $b)$ Mivel négy különböző prímszám összege páratlan, azért az egyik a 2. A szöveg alapján ez a kis zöld kockák száma. A pirosak és a nagy zöldek darabszáma ezek szerint 91. Tudjuk, hogy a piros kockák száma osztható héttel, így a nagy zöldek száma is osztható lesz héttel. Ilyen prímszám csak egy van, ez a 7. Azaz a nagy zöld kockák száma 7. Most már tudjuk, hogy a pirosak száma 84. A feladat állítása szerint nagy piros kockákból ötvennel több van, mint kis piros kockákból. Ezek szerint a nagy pirosból 67 darab, a kis pirosból pedig 17 darab van a dobozban.   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Számadó László</span>}}\hfill \end{array}}$