Kezdőlap


Cím:	Az 52. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Füzet:	2011/október, 386 - 394. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

\begin{matrix} A szerkesztőség \end{matrix}

1. Az

A = {a_{1}, a_{2}, a_{3}, a_{4}}

halmaz négy, páronként különböző pozitív egész számból áll. Az

a_{1} + a_{2} + a_{3} + a_{4}

összeget jelöljük

s_{A}

-val, és jelölje

n_{A}

az olyan

(i, j)

párok

(1 \leq i < j \leq 4)

számát, amelyekre

a_{i} + a_{j}

osztója

s_{A}

-nak.
Határozzuk meg az összes olyan

A

halmazt, amelyre

n_{A}

a lehetséges maximális értékét veszi fel.

Janzer Olivér megoldása. Szimmetria miatt feltehetjük, hogy

a_{1} < a_{2} < a_{3} < a_{4}

.
Először belátjuk, hogy

n_{A} \leq 4

.
Mivel

a_{2} + a_{4} > a_{1} + a_{3}

, tehát

a_{2} + a_{4} > \frac{1}{2} s_{A}

, így nem lehet osztója

s_{A}

-nak (hiszen

a_{2} + a_{4} < s_{A}

). Hasonlóan

a_{3} + a_{4} > a_{1} + a_{2}

, tehát

a_{3} + a_{4} > \frac{1}{2} s_{A}

, így ez sem lehet osztó.
Tehát csak az

(a_{1}, a_{2})

(a_{1}, a_{3})

(a_{1}, a_{4})

(a_{2}, a_{3})

párok jöhetnek szóba, azaz legfeljebb 4 pár. Nézzük meg, ennyi mikor lesz. Mivel

(a_{1} + a_{4})

és

(a_{2} + a_{3})

is osztó, azért

(a_{1} + a_{4}) \leq \frac{1}{2} s_{A}

és

(a_{2} + a_{3}) \leq \frac{1}{2} s_{A}

, így

(a_{1} + a_{2} + a_{3} + a_{4}) \leq s_{A}

. Az egyenlőségnek kell teljesülni:

(a_{1} + a_{4}) = (a_{2} + a_{3}) = \frac{1}{2} s_{A}

(a_{1} + a_{3})

is osztja

s_{A}

-t, ezért

(a_{1} + a_{3}) \leq \frac{1}{3} s_{A}

, hiszen (

a_{1} + a_{3}) < (a_{2} + a_{3}) \leq \frac{1}{2} s_{A}

. Tegyük fel, hogy

(a_{1} + a_{3}) \leq \frac{1}{4} s_{A}

\begin{matrix} \frac{1}{4} s_{A} = \frac{1}{2} (\frac{1}{2} s_{A}) = \frac{1}{2} (a_{2} + a_{3}), \end{matrix}

így

\begin{matrix} a_{1} + a_{3} \leq \frac{1}{2} (a_{2} + a_{3}) \Rightarrow 2 a_{1} + 2 a_{3} \leq a_{2} + a_{3} \Rightarrow 2 a_{1} + a_{3} \leq a_{2}, \end{matrix}

ami

a_{3} > a_{2}

miatt ellentmondás. Így

\frac{1}{4} s_{A} < (a_{1} + a_{3}) \leq \frac{1}{3} s_{A}

, tehát

(a_{1} + a_{3}) = \frac{1}{3} s_{A}

.
Mivel

a_{1} + a_{4} = a_{2} + a_{3}

a_{4} = a_{2} + a_{3} - a_{1}

\begin{matrix} a_{1} + a_{3} & = \frac{1}{3} s_{A} = \frac{1}{3} (a_{1} + a_{2} + a_{3} + a_{4}) = \frac{1}{3} (a_{1} + a_{2} + a_{3} + (a_{2} + a_{3} - a_{1})) = \\ = \frac{1}{3} (2 a_{2} + 2 a_{3}) . \end{matrix}

Így

3 a_{1} + 3 a_{3} = 2 a_{2} + 2 a_{3}

, tehát

a_{3} = 2 a_{2} - 3 a_{1}

\begin{matrix} a_{4} = a_{2} + a_{3} - a_{1} = a_{2} + (2 a_{2} - 3 a_{1}) - a_{1} = 3 a_{2} - 4 a_{1} . \end{matrix}

(a_{1} + a_{2})

is osztója

s_{A}

-nak, de

(a_{1} + a_{2}) < (a_{1} + a_{3}) = \frac{1}{3} s_{A}

, tehát

(a_{1} + a_{2}) \leq \frac{1}{4} s_{A}

. Tegyük fel, hogy

(a_{1} + a_{2}) \leq \frac{1}{6} s_{A}

. Ekkor

\begin{matrix} (a_{1} + a_{2}) \leq \frac{1}{6} (a_{1} + a_{2} + (2 a_{2} - 3 a_{1}) + (3 a_{2} - 4 a_{1})) = \frac{1}{6} (6 a_{2} - 6 a_{1}) = a_{2} - a_{1}, \end{matrix}

amiből

2 a_{1} \leq 0

, ami

a_{1}

pozitív volta miatt ellentmondás.
Tehát

\frac{1}{6} s_{A} < (a_{1} + a_{2}) \leq \frac{1}{4} s_{A}

, így két eset maradt:
1)

\begin{matrix} a_{1} + a_{2} = \frac{1}{4} s_{A} = \frac{1}{4} (a_{1} + a_{2} + (2 a_{2} - 3 a_{1}) + (3 a_{2} - 4 a_{1})) = \frac{1}{4} (6 a_{2} - 6 a_{1}) . \end{matrix}

Így

4 a_{1} + 4 a_{2} = 6 a_{2} - 6 a_{1}

, tehát

10 a_{1} = 2 a_{2}

, azaz

a_{2} = 5 a_{1}

. Ekkor

a_{3} = 2 a_{2} - 3 a_{1} = 7 a_{1}

a_{4} = 3 a_{2} - 4 a_{1} = 11 a_{1}

. Ezek valóban jók, ha

a_{1}

pozitív egész, hiszen

s_{A} = 24 a_{1}

, és

a_{1} + a_{2} = 6 a_{1}

a_{1} + a_{3} = 8 a_{1}

a_{1} + a_{4} = 12 a_{1}

a_{2} + a_{3} = 12 a_{1}

, amik valóban osztók.
2)

\begin{matrix} a_{1} + a_{2} = \frac{1}{5} s_{A} = \frac{1}{5} (6 a_{2} - 6 a_{1}), 5 a_{1} + 5 a_{2} = 6 a_{2} - 6 a_{1}, \end{matrix}

a_{2} = 11 a_{1}

a_{3} = 19 a_{1}

a_{4} = 29 a_{1}

. Így

s_{A} = 60 a_{1}

és

a_{1} + a_{2} = 12 a_{1}

a_{1} + a_{3} = 20 a_{1}

a_{1} + a_{4} = 30 a_{1}

a_{2} + a_{3} = 30 a_{1}

, amik valóban osztók.
Tehát az olyan

A

halmazok a megfelelők, ahol

A = {a,5 a,7 a,11 a}

vagy

A = {a,11 a,19 a,29 a}

és

a

pozitív egész.

2. Legyen

S

a sík pontjainak egy véges, legalább kételemű halmaza. Feltesszük, hogy az

S

halmaz semelyik három pontja sincs egy egyenesen.
Egy szélmalomnak nevezett folyamat során kiindulunk egy

ℓ

egyenesből, amely az

S

halmaznak pontosan egy

P

pontját tartalmazza. Az egyenes a

P

forgástengely körül az óramutató járásával megegyező irányban forog addig, amíg először nem találkozik egy másik,

S

halmazba tartozó ponttal. Ekkor ez a

Q

pont lesz az új forgástengely, és az egyenes a

Q

pont körül forog tovább az óramutató járásával megegyező irányban egészen addig, míg újra nem találkozik egy

S

halmazba tartozó ponttal. Ez a folyamat vég nélkül folytatódik.
Bizonyítsuk be, hogy megválaszthatjuk a

P \in S

pontot és a

P

-n átmenő

ℓ

egyenest úgy, hogy az

S

halmaz minden pontja végtelen sokszor lesz a szélmalom forgástengelye.

Dankovics Attila megoldása. 1. lemma.

a)

A folyamatban megmarad az adott oldalon lévő pontok száma két olyan állapot közt, amikor csak egy pont van az egyenesen.
Bizonyítás. A régi forgástengely a forgó egyenesnek ugyanarra az oldalára kerül, mint amelyik oldalán az új forgástengely volt.

b)

Az 1. lemma hasonlóan belátható két olyan állapotra, amikor két pont van az egyenesen.

2. lemma. Minden ponton megy át olyan egyenes aminek két oldalán ugyanannyi pont van.

Bizonyítás. Veszünk egy egyenest át a ponton, és kitüntetjük az egyik oldalát. Legyen a kitüntetett oldalon

k

-val több pont (feltehetjük, hogy

k

pozitív, illetve ha 0, akkor készen vagyunk). Megforgatjuk az egyenest 180 ponttal, ekkor a kitüntetett oldalon

k

-val kevesebb pont lesz. Mivel nincs 3 pont egy egyenesen, a két oldalon lévő pontok különbsége forgatás közben egyszerre legfeljebb 1-gyel változik. Mivel pozitívból negatívba megy, közben valamikor 0 lesz.

Megoldás. Páratlan sok pont esetén tetszőleges kiindulópontból megfelelő szélmalmot eredményez minden olyan

ℓ

egyenes, amelynek két oldalán ugyanannyi pont van. Ha a pontok száma páros, akkor (egy ilyen egyenest egészen kicsit elforgatva) válasszuk meg

ℓ

-et úgy, hogy az előbbi feltétel az első találkozáskor teljesüljön.

Bizonyítás. Az egyenes iránya körbe fog forogni, eközben az első lemma alapján a két oldalán lévő pontok számának különbsége végig 0 vagy 1. Egy teljes körbefordulás során egy tetszőleges

P

ponton biztosan átmegy akkor, amikor éppen olyan irányú, hogy a

P

-re illeszkedő ilyen irányú

f

egyenesnek ugyanannyi pont van mindkét oldalán. (Ilyen egyenes a 2. lemma szerint valóban létezik.)
Tegyük fel ugyanis, hogy az

e

egyenesünk ilyen irányú, de nem megy át

P

-n ‐ ugyanakkor tartalmazza a halmaz egy

Q

pontját. Az

f

-et nemnulla eltolás viszi

e

-be, melynek eredményeként eltávolodik

P

-től, és rákerül a

Q

. Így az

e

P

-t tartalmazó oldalán legalább kettővel több pont lenne, mint a másikon, ami ellentmondás.
Ezzel a feladatot megoldottuk.

3. Legyen

f : R \to R

egy olyan függvény, amelyre teljesül az

\begin{matrix} f (x + y) \leq y f (x) + f (f (x)) \end{matrix}

feltétel minden

x

y

valós számra. Bizonyítsuk be, hogy minden

x \leq 0

esetén teljesül

f (x) = 0

Kalina Kende megoldása. Az

f (x + y) \leq y f (x) + f (f (x))

egyenlőtlenségből

y = 0

helyettesítéssel:

\begin{matrix} f (x) \leq f (f (x)) . \end{matrix}

(1)

Ha van olyan

a

, amelyre

f (a) = 0

, akkor

\begin{matrix} f (b + a) \leq b f (a) + f (f (a)) = f (0) . \end{matrix}

Mivel

a + b

minden valós értéket felvesz, minden

c

-re teljesül:

\begin{matrix} f (c) \leq f (0), \end{matrix}

(2)

speciálisan

f (f (0)) \leq f (0)

. Innen (1) miatt

f (0) = f (f (0))

. Ezt felhasználva:

\begin{matrix} f (0) = f (f (0) - f (0)) \leq - f {(0)}^{2} + f (f (0)) . \end{matrix}

Mivel így

0 \leq - f {(0)}^{2}

, ebből

f (0) = 0

.
Legyen

k < 0

\begin{matrix} 0 = f (k - k) \leq - k f (k) + f (f (k)), így k f (k) \leq f (f (k)) . \end{matrix}

(2) alapján a jobb oldal kisebb vagy egyenlő, mint

0

, így a bal oldal is. Mivel

k < 0

, és (2) alapján

f (k) \leq 0

, így

f (k) = 0

lehet csak.
Tehát, ha találunk egy gyököt, az állítás igaz. Így a továbbiakban indirekt felteszem, hogy

f (x) \neq 0

minden

x

-re. Alkalmazzuk a következő helyettesítést:

\begin{matrix} f (q) \leq (q - r) f (r) + f (f (r)), f (q) \leq q f (r) - r f (r) + f (f (r)) . \end{matrix}

(3) Ebből látszik, hogy ha van olyan

r

, amelyre

f (r) > 0

, akkor

f (q)

mindig negatív, amennyiben

q

kisebb egy adott

Q

értéknél. Ha nincs ilyen

r

, akkor ugyanez bármilyen

Q

-ra igaz.
Legyen

y = f (x) - x

; ekkor:

\begin{matrix} 0 \leq (f (x) - x) f (x), azaz x f (x) \leq f {(x)}^{2} . \end{matrix}

(4) Innen a függvény negatívakon felveheti a következő értékeket: pozitív valósak, abszolút értékben

x

-nél nagyobb vagy egyenlő (tehát

x

-nél kisebb vagy egyenlő) negatív valósak.
Legyen

h

a (3) szerinti

Q

-nál kisebb negatív valós szám. Ekkor

f (h) \leq h

; és

f (f (h)) \leq f (h)

. Viszont (1) miatt

f (h) \leq f (f (h))

, így

f (h)

fixpont. Illetve egy másik,

j < f (h)

-ra

f (j) = j < f (h)

is fixpont.
Az eredeti egyenlőtlenséget a negatív

a < b

fixpontokból képzett

a

és

b

-a számokra felírva:

\begin{matrix} f (a + (b - a)) \leq (b - a) f (a) + f (f (a)), b \leq (b - a) a + a, b - a \leq (b - a) a . \end{matrix}

Mivel

a < b

, azaz

b - a > 0

, ebből

1 \leq a

, ami ellentmondás. Tehát a megoldás első fele szerint következik a feladat állítása.

4. Legyen

n > 0

egy egész szám. Van egy kétkarú mérlegünk és

n

súlyunk, amelyek súlya

2^{0}

2^{1}, ..., 2^{n - 1}

. Ezt az

n

súlyt egymás után a mérlegre akarjuk helyezni oly módon, hogy a jobboldali serpenyő soha ne legyen nehezebb a baloldali serpenyőnél. Mindegyik lépésben kiválasztjuk az eddig a mérlegre nem tett súlyok valamelyikét, és a mérlegnek vagy a baloldali vagy a jobboldali serpenyőjébe helyezzük, egészen addig, amíg az összes súly fel nem kerül a mérlegre.
Határozzuk meg, hogy hányféleképpen lehet ezt megtenni.

Damásdi Gábor megoldása.

N

darab súlyt

1 \cdot 3 \cdot 5 \cdot ... \cdot (2 n - 1)

-féleképpen lehet jól felrakni a mérlegre. Ezt indukcióval látjuk be:

n = 1

és

n = 2

könnyen ellenőrizhető. Tegyük fel, hogy valamilyen

n

-re

1 \cdot 3 \cdot 5 \cdot ... \cdot (2 n - 1)

-féle jó felrakás van. Azt kell belátnunk, hogy

n + 1

súlyt

2 n + 1

-szer annyi módon rakhatunk fel, mint

n

súlyt.
Vegyük az

n

súlynak egy tetszőleges felrakását. A következő módon csinálunk belőle egy felrakást

n + 1

súlyra: minden elem tömegét megkétszerezzük, majd valahova beszúrunk még egy lépést, amiben egy 1 tömegű súlyt helyezünk fel.
A kétszerezés miatt megkapjuk a

2,4, ..., 2^{n}

tömegű súlyokat, és beszúrjuk az 1 tömegűt, tehát ez tényleg

n + 1

súly felrakása. A kétszerezés nem rontja el a nagyságviszonyt. Mivel a kétszerezés után a tömegek párosak, az 1 tömegű súly csak akkor rontja el a felrakást, ha legelőre szúrjuk be és a jobb oldalra rakjuk. Tehát egy esetet kivéve, bármikor bármelyik oldalra felrakhatjuk az 1 tömegű súlyt, így

2 n + 1

darab felrakást készítettünk

n + 1

súlyra. Ezután elég belátni, hogy ezzel a módszerrel minden felrakás elérhető

n + 1

súlyra és egyik se érhető el kettő különböző

n

súlyos felrakásból.
Minden felrakás elérhető

n + 1

súlyra, mivel visszafelé is megadhatjuk a módszert: vegyünk egy felrakást

n + 1

súlyra. Vegyük ki azt a lépést, amiben az 1 tömegű súlyt rakjuk fel, és osszuk el a tömegeket 2-vel. Így egy felrakást kapunk

n

súlyra, amiből elérhető a kiinduló felrakás

n + 1

súlyra.
Ha különböző felrakásokból indulunk ki, a

2,4, ..., 2^{n}

tömegű súlyok más sorrendben lesznek az

n + 1

súlyos felrakásban, azaz minden felrakást csak egy módon érhetünk el.
Minden felrakásból készítettünk

2 n + 1

felrakást

n + 1

súlyra, tehát beláttuk az indukciót.

5. Jelölje

Z

az egész számok halmazát,

N

pedig a pozitív egész számok halmazát. Legyen

f

egy

Z

-t

N

-be képező függény. Tegyük fel, hogy bármilyen két

m

és

n

egész szám esetén az

f (m) - f (n)

különbség osztható

f (m - n)

-nel.
Bizonyítsuk be, hogy minden

m

n

egész számra teljesül az, hogy ha

f (m) \leq f (n)

, akkor

f (n)

osztható

f (m)

-mel.

Nagy Donát megoldása. (1) Az

n

helyébe 0-t írva

f (m) ∣ f (m) - f (0)

, így

f (m) ∣ f (0)

minden

m

-re.
(2)

m

helyébe 0-t írva

f (- n) ∣ f (0) - f (n)

, innen (1) miatt

f (- n) ∣ f (n)

minden

n

-re;
(3) és itt

n

helyébe

- n

-et írva

f (n) ∣ f (- n)

, de mivel

f (n)

és

f (- n)

is pozitív egész, azért

f (n) = f (- n)

minden

n

-re.
A bizonyítandó állítás lényegében az, hogy

f

értékkészletének bármely két eleme közül egyik osztója a másiknak. Legyenek

a

és

b

tetszőleges egészek, ekkor

m

helyébe

a

-t,

n

helyébe

b

-t írva

f (a - b) ∣ f (a) - f (b)

, illetve

m

helyébe

a

-t,

n

helyébe

(a - b)

-t írva

f (a - (a - b)) = f (b) ∣ f (a) - f (a - b)

, végül

m

helyébe

(b - a)

-t,

n

helyébe

b

-t írva

f ((b - a) - b) = f (- a) ∣ f (b - a) - f (- b)

. (3) felhasználásával ezek azt adják, hogy az

f (a)

f (b)

és

f (a - b)

pozitív egészek közül bármely kettő különbsége osztja a harmadikat. Ha az

x

y

z

pozitív egészek közül bármely kettő különbsége osztja a harmadikat és például

x

az egyik legnagyobb közülük, akkor

- x \leq - z < y - z < y \leq x

, de így mivel

x ∣ (y - z)

, azért

y - z = 0

y = z

és ekkor

y ∣ (z - x)

-ből

y = z ∣ x

adódik, így ekkor

x

y

és

z

közül bárhogyan választunk kettőt, egyikük osztani fogja a másikat. Ezt az

f (a)

f (b)

f (a - b)

hármasból

f (a)

-t és

f (b)

-t választva alkalmazva adódik a feladat állítása, hiszen

a

és

b

tetszőleges egészek voltak.

6. Legyen

A B C

egy hegyesszögű háromszög,

Γ

a háromszög körülírt köre és

ℓ

Γ

egy érintőegyenese. Jelölje

ℓ_{a}

ℓ_{b}

ℓ_{c}

azokat az egyeneseket, amelyeket úgy kapunk, hogy

ℓ

-et a

B C

C A

, illetve

A B

egyenesekre tükrözzük.
Bizonyítsuk be, hogy az

ℓ_{a}

ℓ_{b}

ℓ_{c}

egyenesek által meghatározott háromszög körülírt köre érinti a

Γ

kört.

Nagy János megoldása. Legyenek az

ℓ_{b}

ℓ_{c}

és

ℓ_{a}

egyenesek által meghatározott háromszög csúcsai rendre

A'

B'

és

C'

; és legyen az

A' B' C'

háromszög körülírt köre

Γ'

, ekkor azt kell igazolnunk, hogy

Γ'

és

Γ

körök érintik egymást.
A

Γ

kör és az

A' B' C'

háromszög, illetve

Γ'

kör között csak gondolati kapcsolat van eddig, kell valami, ami fizikaivá teszi. Ehhez vegyük észre, hogy az

A' B' C'

háromszög beírt körének

I

középpontja rajta van a

Γ

körön és ráadásul az

I A

I B

I C

egyenesek átmennek rendre az

A'

B'

és

C'

pontokon.

Ezt az állításunkat nem fogjuk bebizonyítani, mert nincs is rá szükség, elég ha tudjuk intuitívan, hogy ez igaz. Legyenek az

A B C

háromszög szögei

α

β

γ

, amik tehát hegyesszögek.
Most a következőt fogjuk belátni: Legyen

A' B' C'

egy háromszög, melynek szögei

\begin{matrix} 180^{\circ} - 2 α, 180^{\circ} - 2 β és 180^{\circ} - 2 γ, \end{matrix}

ennek körülírt köre

k'

, beírt körének középpontja

I

, és

k

egy olyan kör, ami átmegy az

I

ponton, és érinti a

k'

kört. A

k

kör és az

I A'

I B'

I C'

egyenesek második metszéspontja

A

B

és

C

. Ekkor az

A B

egyenesre tükrözve az

A' B'

egyenest, a

B C

egyenesre tükrözve a

B' C'

egyenest és a

C A

egyenesre tükrözve a

C' A'

egyenest, ugyanazt az egyenest kapjuk, ami ráadásul érinti a

k

kört.
Egyrészt belátjuk ezt az állítást, másrészről megmutatjuk, hogy ebből következik a feladat állítása:
Először is ebben a helyzetben az

A B C

háromszög szögei

α

β

és

γ

, mert a

k

körben a kerületi szögek tétele miatt a háromszög szögei megegyeznek az

A' B' C'

háromszög szögfelezőinek egymással bezárt szögeivel, amik éppen

α

β

és

γ

.
Most tekintsük a fix

A' B'

egyenes

A B

egyenesre való tükörképét.
Ha a

k

kör helyzetét közben változtatjuk, akkor könnyen látható, hogy az

A B

egyenes minden irányt fel fog venni

k

összes helyzetét tekintve, mert minden irányhoz tudunk találni olyan kört, amely átmegy

I

-n, és akkor ezt hasonlósággal át tudjuk vinni olyanba, ami érinti a

k'

kört.
Így tehát az

A B

egyenes és a tükörkép szöge is tetszőleges lehet, az egyéb diszkussziós meggondolásokat most mellőzzük.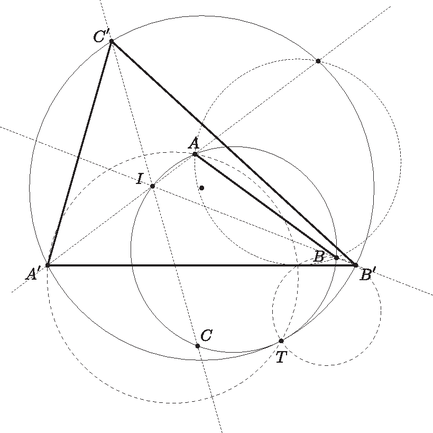

Van tehát olyan helyzete a

k

körnek, amelyre az

A

B

C

és a közös tükörképek érintési pontja a

k

körrel; e négy pont által meghatározott négyszög hasonló az eredeti feladatban levő

A B C P

négyszöghöz. De ekkor a hasonlóság az eredeti feladat két körét az itteni

k

és

k'

körökbe viszi, amik érintik egymást, tehát ekkor készen lennénk.
Most tehát igazoljuk az állításunkat. Az, hogy a tükörképek érintik a

k

kört, szimmetrikus állítások, így elég közülük az egyiket igazolni, mi az

A' B'

egyenes tükörképével tesszük ezt.
Ehelyett azt látjuk be, hogy ha az

A B

egyenesre tükrözzük a

k

kört, akkor az érinti az

A' B'

egyenest valamilyen

X

pontban, ami természetesen ekvivalens átfogalmazás.
Azt kell észrevenni még, hogy ez az

X

pont rajta lesz az

A' A T

háromszög, illetve a

B' B T

háromszög körülírt körén is.
Tehát megmutatjuk, hogy az

A' A T

háromszög, illetve a

B' B T

háromszög körülírt köre az

A' B'

egyenesen metszi egymást, utána pedig belátjuk, hogy ez az

X

metszéspont rajta van a tükrözött körön, sőt érintési pont is egyben.
Először is lássuk be, hogy az

A' A T

háromszög, illetve a

B' B T

háromszög körülírt köre az

A' B'

egyenesen metszi egymást, tegyük fel hogy az első kör metszéspontja az

A' B'

egyenessel

X_{1}

, a másodiké pedig

X_{2}

; azt akarjuk belátni, hogy

X_{1} = X_{2}

.
Ehhez az kell, hogy

\begin{matrix} T X_{1} A' ∢ + T X_{2} B' ∢ = 180^{\circ}, \end{matrix}

\begin{matrix} T X_{1} A' ∢ + T X_{2} B' ∢ = T A A' ∢ + T B B' ∢ = I A T ∢ + 180^{\circ} - I B T ∢ = 180^{\circ}, \end{matrix}

ahol végig a kerületi szögek tételét használtuk.
Legyen tehát

X = X_{1} = X_{2}

, belátjuk, hogy

X

rajta van az

A B

-re tükrözött

k

körön; ehhez azt kell igazolnunk, hogy

\begin{matrix} A X B ∢ = 180^{\circ} - A T B ∢ = 180^{\circ} - A I B ∢ = 180^{\circ} - γ, \end{matrix}

\begin{matrix} A X B ∢ & = 180^{\circ} - A X A' ∢ - B X B' ∢ = 180^{\circ} - A T A' ∢ - B T B' ∢ = \\ = 180^{\circ} - γ - A T A' ∢ - B T B' ∢ + γ = 180^{\circ} - γ . \end{matrix}

Felhasználtuk, hogy

A' T B' C'

húrnégyszög.
Ezzel megkaptuk, hogy

X

rajta van a tükrözött körön is, még az kell, hogy érintési pont is egyben.
Ehhez invertáljuk az ábrát a

T

pontból, ekkor a képábrán

A

A'

és

X

képei egy egyenesen lesznek, és

B

B'

és

X

képei is egy egyenesen lesznek az inverzió szabályai szerint.
Ezen kívül

A B

képe párhuzamos lesz

A' B'

képével, mert az eredeti ábrán az

A B T

kör érinti az

A' B' T

kört, így tehát a képábrán az

X A B

és

X A' B'

háromszögek hasonlóak, tehát körülírt körük érintik egymást.

Ezeknek a köröknek az ősképei az

A X B

kör, illetve az

A' B'

egyenes, mert

A'

X

és

B'

egy egyenesen vannak az eredeti ábrán, ezért az inverzió szögtartása miatt az

A' B'

egyenes az eredeti ábrán valóban érinti az

A X B

körülírt körét, vagyis a tükrözött kört.
Ezzel bebizonyítottuk, hogy ha az

A B

egyenesre tükrözzük az

A' B'

egyenest, akkor a kép érinti a

k

kört, és ugyanígy a többi csúcspárra is, már csak azt kéne belátni, hogy ez az érintési pont mind a három alkalommal ugyanaz lesz.
Legyen az

A

B

csúcspárra ez az érintési pont

E_{1}

, a

B

C

csúcspárra pedig

E_{2}

, ekkor a szimmetria miatt elég belátni hogy

E_{1} = E_{2}

, és akkor mindhárom érintési pontnak meg kell egyeznie.
Tehát tudjuk, hogy

X A B ∢ = B X B' ∢

az érintő szárú kerületi szögek tétele miatt, és akkor a bizonyítottak szerint

E_{1} A B ∢ = X A B ∢ = B X B' ∢ = B T B' ∢

.
Teljesen szimmetrikusan

E_{2} A B ∢ = E_{2} C B ∢ = B T B' ∢

, abból pedig akkor az

E_{1}

és

E_{2}

pontnak meg kell egyezni, vagy tükrösnek kell lennie az

A B

egyenesre; de ezt mindegyik

E_{i}

E_{j}

párra elmondhatjuk a szimmetria miatt és akkor ez már csak tényleg úgy lehet, hogy ha az

E_{1}

E_{2}

E_{3}

pontok megegyeznek: ha közülük semelyik kettő nem egyezne meg, akkor a felező merőlegeseik egy ponton mennének át, de ez az

A B

A C

B C

oldalakra nyilván nem teljesül. Ha pedig kettő megegyezik, a harmadik meg más, akkor két felező merőleges teljesen megegyezne, ami megint csak nem teljesülhet két oldalra.
Így tehát igazoltuk az állításunkat, és ‐ mint azt korábban megmutattuk ‐ ezzel bizonyítottuk az eredeti feladat állítását is.