A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.Megoldásvázlatok a 2012/6. sz. emelt szintű gyakorló feladataihoz
I. rész
1. Adott a valós számok halmazán értelmezett és függvény:
Igazoljuk, hogy elsőfokú függvény.
Adjuk meg a függvény zérushelyeit. (11 pont)
Megoldás. A hozzárendelési szabályban megadott képlet a következő módon egyszerűbb alakra hozható: | |
Vagyis valóban elsőfokú függvény.
A választ az egyenlet megoldásai adják. Ha , akkor az egyenlet az alakot veszi föl, azaz . A három tényező bármelyike lehet nulla, nekünk a feltétel miatt most az és az a megfelelő. Ha , akkor az egyenlet formában is írható, azaz . A második tényező minden valós esetén pozitív, az első tényező pedig nulla esetén lesz nulla. Vagyis a vizsgált feltétel mellett nincs egyetlen megfelelő érték sem.
Vagyis a függvénynek két zérushelye van, a 0 és a 2.
2. Egy szabályos hatszög oldalai és átlói közül ötöt pirosra, a többit zöldre festettük. Ezek után véletlenszerűen választunk közülük öt szakaszt. Mennyi annak a valószínűsége, hogy pontosan három piros és kettő zöld lesz a kiválasztottak között? (13 pont)
Megoldás. A szabályos hatszögnek 6 oldala és 9 átlója van. A 15 szakasz között lesz 5 piros és 10 zöld. Először meghatározzuk az összes lehetőségek számát. A 15 szakasz közül ötöt választunk (a sorrend nem számít). Ezt -féleképpen tehetjük meg. Ezután a vizsgált esemény szempontjából kedvező esetek számát is összeszámoljuk. A három piros szakaszt az öt pirosból, a két zöldet a tíz zöldből kell választanunk (a sorrend itt sem számít).
Ez -féleképpen történhet.
A keresett valószínűség: .
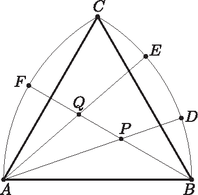
3. Az egy szabályos háromszög. Az középpontú sugarú kör kisebbik ívének -hez közelebbi harmadolópontja , -hez közelebbi harmadolópontja pedig . A középpontú sugarú kör kisebbik ívének felezőpontja . Mekkorák az , és egyenesek által meghatározott háromszög belső szögei? (13 pont)
Megoldás. Legyen és metszéspontja , és metszéspontja pedig .
Az háromszög belső szögeinek nagyságát kell megadnunk. Az szabályos háromszög minden szöge -os. A feladat szövegéből következik a kerületi szögek tétele szerint, hogy és harmadolja a szabályos háromszög csúcsánál található -os szöget. Ezért az háromszögben az csúcsnál -os, és a háromszögben is az csúcsnál -os szög van. A kerületi szögek tétele szerint a egyenes felezi a szabályos háromszög csúcsánál található -os szöget. Tehát .
Az háromszög csúcsánál található külső szög azonos az háromszög csúcsánál található belső szöggel, azaz az háromszög két másik belső szögének összegével egyenlő: .
Két belső szög ismeretében a harmadik kiszámolható: . Vagyis a kérdésben szereplő háromszög szögei: , , .
4. Az háromszög csúcsainak koordinátái: , és .
Milyen hosszú a háromszög legrövidebb magassága?
Mekkora a háromszög területe?
Egyszerre dobunk egy piros és egy zöld dobókockával. A pirossal dobott szám legyen egy pont első, a zölddel dobott szám a második koordinátája. Mekkora valószínűséggel lesz az így kapott pont az háromszög belsejében? (14 pont)
Megoldás. A legrövidebb magasság a leghosszabb oldalhoz tartozik. Az oldalak hosszát meghatározzuk a két pont távolságát megadó képlettel:
Vagyis az csúcs és a oldalegyenes távolsága adja a keresett magasság hosszát.
Számolásunk szerint az egyenlő szárú háromszög, hiszen . A keresett magasság az alaphoz tartozik, aminek talppontja az oldal felezőpontja is egyben: , vagyis a keresett magasság hossza:
A és a ismeretében a terület:
Megjegyzés. Természetesen az előző rész nélkül, közvetlenül is meghatározható a terület. Az négyzetből (ahol , és koordinátájú pontok) levágjuk az , és derékszögű háromszögeket.
Vagyis: (és ebből szintén megkapható, hogy ).
A háromszög csúcsai közül az abszcisszája a legkisebb, a abszcisszája a legnagyobb. Ezért a háromszög belsejében lévő pontok első koordinátája 2, 3, 4 vagy 5 lehet. Ezekhez az esetekhez gyorsan meghatározhatók a megfelelő második koordináták: | |
Ezek mindegyike lehet a dobókockák dobásának eredménye, így a kedvező esetek száma 10.
Az összes esetek száma (a két dobókocka dobásával előállítható pontok száma): . A keresett valószínűség:
II. rész
5. Egy érettségi találkozón Lászlótól -ben megkérdezték tanítványai, hogy hány éves. Ezt válaszolta:
,,Édesanyám születési évszáma , az én születési évszámom pedig , ekkor ő éves volt. Nem egy városban élünk, a következő héten utazom hozzá.''
Hány éves László -ben? (16 pont)
Megoldás. Mivel László 2012-ben a már korábban érettségizett tanítványaival beszélgetett, ezért ő a 20. században született. A következő héten meglátogatja édesanyját, így ő is biztosan a 20. században született. Ha élne 112 évnél idősebb asszony hazánkban, arról biztosan értesültünk volna a médiából. (A legidősebb magyar 2012. április 27-én 110 éves volt.) Vagyis csak az , jöhet szóba.
A szöveg szerint:
Mivel a bal oldal osztható 10-zel, ezért a jobb oldalon is 10-zel osztható számnak kell állnia. Tehát a számjegy lehetséges értékei: 6, 5, 1, 0. A négy eset mindegyikéhez egy-egy másodfokú egyenlet tartozik. Ezek közül nekünk azok az esetek lesznek megfelelőek, amelyeknek van számjegy megoldása.
A másodfokú egyenletek a következők lesznek:
I. eset. Ha , akkor . Nem kapunk -re számjegyet.
II. eset. Ha , akkor . Nem kapunk -re számjegyet.
III. eset. Ha , akkor . Nem kapunk -re számjegyet.
IV. eset. Ha , akkor . Innen a megfelelő.
Az egyedüli megoldás: , , , .
Azaz László születési évszáma , vagyis 2012-ben 51 éves.
6. Tekintsük az sorozatot .
Határozzuk meg a sorozat összes olyan tagját, amelyek -nál nem kisebbek.
Az , , sorszámai egy mértani sorozat három egymást követő tagját adják. Igazoljuk, hogy a sorozat ezen három eleme egy számtani sorozatnak a három egymást követő tagja lesz.
Hány olyan tagja van a sorozatnak, amelyek három tizedes jegyre kerekített értéke
Határozzuk meg a értékét. (16 pont)
Megoldás. Határozzuk meg a sorozat első néhány tagját: | |
Ezek a tagok megfelelőek. Megmutatjuk, hogy több nincs, mert a sorozat szigorúan monoton csökkenő, azaz a | |
egyenlőtlenség minden pozitív egész esetén teljesül.
Szorozhatjuk az egyenlőtlenség mindkét oldalát -gyel, hiszen pozitív egész -ek esetén ez a szorzat pozitív:
Ez pedig valóban igaz, vagyis a sorozat szigorúan monoton csökkenő.
Tehát a sorozatnak csak az első, a második és a harmadik tagja nem kisebb 3-nál.
A sorozat kérdéses három tagja a következő: , , .
Mivel , így ezek a számok valóban egy számtani sorozat három egymást követő tagját adják.
A feladat feltétele szerint azokat a pozitív egész -eket keressük, amelyekre
Szorozhatjuk az egyenlőtlenséget -mal, hiszen pozitív egész -ek esetén ez pozitív:
Az első egyenlőtlenségből kapjuk: . A második egyenlőtlenségből kapjuk: . Vagyis az lehetséges értékei: 478, 479, , 517, 518. Ez összesen 41 tag.
A határérték tulajdonságait felhasználva: | |
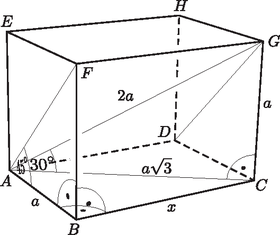
7. Az téglatestben úgy jelöltük a csúcsokat, hogy az alaplappal egybevágó lapon az csúcsot az -val, a csúcsot a -vel, a csúcsot a -vel, a csúcsot a -vel kösse össze él. Tudjuk, hogy a szög -os, a szög pedig -os.
Igazoljuk, hogy négyzet.
Mekkora az tetraéder felszíne, ha ?
Mekkora az tetraéder térfogata, ha és távolsága ?
(16 pont)
Megoldás. Használjuk az ábra jelöléseit. Mivel a téglatest oldallapján az átló szögfelező (), ezért ez a lap négyzet. Az oldalai legyenek hosszúságúak, ekkor . Tudjuk, hogy a derékszögű háromszögben , és , ezért , .
Az derékszögű háromszögben a Pitagorasz-tétel alapján: Vagyis a téglatest ezzel párhuzamos minden éle hosszúságú. Téglatest esetén az metszetről tudjuk, hogy téglalap, most pedig az is kiderült, hogy két szomszédos oldala egyenlő: , ezért valóban négyzet.
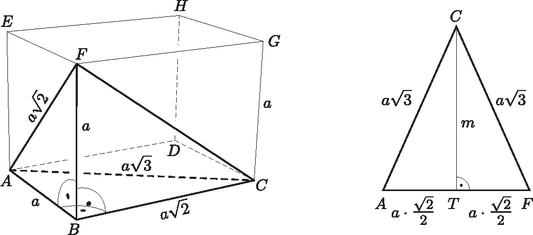
Az tetraéder felszíne három derékszögű háromszögből: , és , valamint az egyenlő szárú háromszögből áll.
, hiszen mindkettő ugyanolyan téglalapnak az átlója. Az háromszögben a magasság hossza Pitagorasz-tétellel kifejezhető: A tetraéder felszíne:
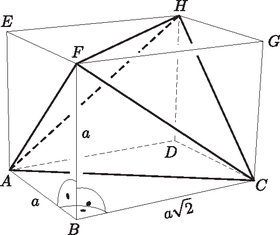
Az téglatest , , és csúcsába is ugyanolyan hosszúságú három él fut be: , , . Az ezek által kifeszített négy tetraédert kell levágnunk a téglatestből, hogy megmaradjon az tetraéder. Az eddigi számolásunk azt mutatja, hogy ha az és távolsága , akkor .
Egy levágott tetraéder térfogata:
Vagyis a feladatban szereplő tetraéder térfogata: | |
8. Egy ház tűzfala egy négyzetből és egy szabályos háromszögből áll. A falat két színnel szeretnék vakolni. A két rész között a határvonal egy parabola lesz, amit a mellékelt ábra mutat. A házikó parabola feletti részét világosabbra, a többit sötétebbre vakolják. A felület hány százaléka lesz sötétebb árnyalatú? (16 pont)
Megoldás. Legyen a négyzet oldala 4, ekkor a tűzfal területe:
Meghatározzuk a sötétebb rész területét. Ehhez az ábrát koordináta-rendszerbe tesszük. A parabola az hozzárendeléssel megadott függvény képe. Az egyenes illeszkedik a pontra, és mivel az irányszöge , azért az iránytangense: . Ezek segítségével megadható, hogy az egyenes egyenlete: , vagyis az egyenes a hozzárendeléssel megadott függvény képe. Meghatározzuk a parabola és az egyenes metszéspontjának koordinátáit.
Az egyenlet megoldása adja a metszéspontok első koordinátáját:
A két gyök közül az egyik negatív, most arra a metszéspontra van szükségünk, amelynek az első koordinátája pozitív: . A kérdéses területet a következő módon kapjuk:
Ez az egésznek kb. a 33,2%-a.
Megjegyzés. A második integrál helyett használhatjuk a trapéz területképletét is.
9. Határozzuk meg azokat az valós számokat, amelyre és négyzetösszege a négyzetével egyenlő.
(16 pont)
Megoldás. A egyenletet kell megoldanunk. Ezt az egyenletet alakra tudjuk hozni.
Tovább alakítva:
A -re háromféle értéket kapunk:
I. eset: , ahonnan , .
II. eset: , tehát nem ad megoldást.
III. eset: , ahonnan , ,
, , vagyis , .
Tehát a feladat feltételeinek megfelelő összes valós számot az , , adja.
Számadó László
|
|
 PDF | MathML
PDF | MathML