Cím:	Az 53. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Füzet:	2012/október, 386 - 395. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Az 53. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai   A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.     ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">A szerkesztőség</span>}}\hfill \end{array}}$     1. Az $ABC$ háromszög $A$ csúccsal szemközti hozzáírt körének középpontja $J$. Ez a hozzáírt kör a $BC$ oldalt az $M$ pontban, az $AB$, ill. $AC$ egyeneseket pedig a $K$, ill. $L$ pontban érinti. Az $LM$ és $BJ$ egyenesek metszéspontja $F$, a $KM$ és $CJ$ egyenesek metszéspontja pedig $G$. Legyen $S$ az $AF$ és $BC$ egyenesek metszéspontja, $T$ pedig a $AG$ és $BC$ egyenesek metszéspontja. Bizonyítsuk be, hogy $M$ az $ST$ szakasz felezőpontja. (Az $ABC$ háromszög $A$ csúccsal szemközti hozzáírt köre az a kör, amelyik érinti a $BC$ szakaszt, továbbá az $AB$ félegyenes $B$-n túli részét és az $AC$ félegyenes $C$-n túli részét.)   Sándor András megoldása. Az $ABC$ háromszög szögeit jelölje a szokásos módon 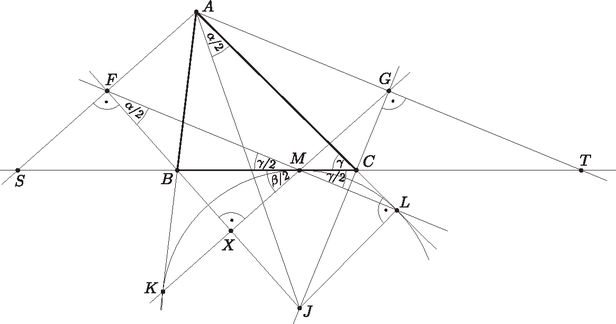$\alpha$, $\beta$ és $\gamma$.   $FMB\sphericalangle =LMC\sphericalangle =\frac{\gamma }{2}$, mert az $CLM$ háromszög egyenlő szárú és a $C$-nél levő szöge az $ABC$ háromszög $\gamma$-hoz tartozó külső szöge. Hasonlóan $BMK\sphericalangle =\frac{\beta }{2}$. Jelölje az $MK$ és $JF$ szakaszok metszéspontját $X$; ekkor $MXF\sphericalangle ={90}^{\circ }$, mert a $BMK$ háromszög egyenlő szárú, és $BJ$ felezi a $B$-nél lévő szöget, ezért merőleges az $MK$ alapra. Így ${\displaystyle \begin{array}{cc}\hfill {\displaystyle LFJ\sphericalangle }& {\displaystyle =MFX\sphericalangle ={180}^{\circ }-FMX\sphericalangle -MXF\sphericalangle =}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={180}^{\circ }-FMB\sphericalangle -BMX\sphericalangle -MXF\sphericalangle ={180}^{\circ }-\frac{\gamma }{2}-\frac{\beta }{2}-{90}^{\circ }=\frac{\alpha }{2}\mathrm{.}}\hfill \end{array}}$ $LAJ\sphericalangle =\frac{\alpha }{2}$, mert az $A$-hoz tartozó belső szögfelező átmegy a hozzáírt kör középpontján. Ebből és az $LFJ\sphericalangle$-re kapott eredményből következik, hogy $ALJF$ húrnégyszög. $ALJ\sphericalangle ={90}^{\circ }$, hiszen $AL$ érintő, tehát a vele szemközti $JFA\sphericalangle$ is ${90}^{\circ }$. $GX$ párhuzamos $AS$-sel, mivel $GXF\sphericalangle ={90}^{\circ }$. Az előbbiekhez hasonlóan $JGA\sphericalangle ={90}^{\circ }$. Így $G$ felezi az $AT$ szakaszt, mivel a $JG$-re való tükrözésnél az $AL$ egyenes képe az $MT$ egyenes, az $AT$ egyenes helyben marad, tehát $A$ képe $T$. Emiatt az $ATS$ háromszögben a $GM$ középvonal, tehát $M$ felezi $ST$-t. (A megoldás független az ábrától.)     2. Legyen $n\ge 3$ egész, és legyenek $a_2\mathrm{,}{a}_3\mathrm{,}\text{...}\mathrm{,}{a}_n$ olyan pozitív valós számok, amelyekre $a_2{a}_3\cdots a_n=1$. Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle {\left(1+a_2\right)}^2{\left(1+a_3\right)}^3\text{...}{\left(1+a_n\right)}^n>n^n\mathrm{.}}\end{array}$     Ágoston Tamás megoldása.   Ha $i\ge 2$ egész, akkor az $\frac{1}{i-1}$, $\frac{1}{i-1}$, $\text{...}$, $\frac{1}{i-1}$, $a_i$ pozitív számokra (az $\frac{1}{i-1}$ szám $\left(i-1\right)$-szer szerepel) alkalmazhatjuk a számtani és mértani közepek közti egyenlőtlenséget: $\begin{array}{c}{\displaystyle \frac{\left(i-1\right)\frac{1}{i-1}+a_i}{i}\ge \sqrt[i]{\frac{a_i}{{\left(i-1\right)}^{i-1}}}\mathrm{.}}\end{array}$   Ezt $i$-edik hatványra emelve, és szorozva a bal oldali nevezővel: $\begin{array}{c}{\displaystyle {\left(1+a_i\right)}^i\ge \frac{i^i}{{\left(i-1\right)}^{i-1}}{a}_i\mathrm{.}}\end{array}$ (1) Ha $i\in \left\{\mathrm{2,3,}\text{...}\mathrm{,}n\right\}$, akkor itt mindkét oldal pozitív, így ezekre az $i$-kre összeszorozva $\left(1\right)$-et: $\begin{array}{c}{\displaystyle {\left(1+a_2\right)}^2{\left(1+a_3\right)}^3\cdot \text{...}\cdot {\left(1+a_n\right)}^n\ge \frac{2^2}{1^1}\cdot \frac{3^3}{2^2}\cdot \text{...}\cdot \frac{n^n}{{\left(n-1\right)}^{n-1}}{a}_2{a}_3\cdot \text{...}\cdot a_n=n^n\mathrm{.}}\end{array}$ Itt használjuk azt a feltételt, hogy $a_2{a}_3\cdot \text{...}\cdot a_n=1$. Azt kell még belátnunk, hogy egyenlőség nem állhat fenn. Mivel $\left(1\right)$-ben a kérdéses $i$-kre mindkét oldal pozitív, a szorzatban egyenlőség pontosan akkor áll, ha minden $i$-re $\left(1\right)$-ben egyenlőség áll. Ez pedig pontosan akkor igaz, ha minden $i$-re a számtani és mértani közepeket egyenlő számokra vettük, azaz $a_i=\frac{1}{i-1}=\text{...}=\frac{1}{i-1}$. Ekkor viszont $a_2{a}_3\cdot \text{...}\cdot a_n=1\cdot \frac{1}{2}\cdot \text{...}\cdot \frac{1}{n-1}$, ahol minden tényező pozitív, és $1$-nél nem nagyobb. Viszont $n\ge 3$ miatt az $1$-nél kisebb $\frac{1}{2}$ tényező is szerepel, vagyis a szorzat kisebb $1$-nél. Ez ellentmond a feladat feltételének, így valóban nem állhat fenn egyenlőség, azaz $\begin{array}{c}{\displaystyle {\left(1+a_2\right)}^2{\left(1+a_3\right)}^3\cdot \text{...}\cdot {\left(1+a_n\right)}^n>n^n\mathrm{,}}\end{array}$ és ezt akartuk bizonyítani.     3. A hazudós játékot két játékos játssza: $A$ és $B$. A játék szabályaiban szerepel két pozitív egész szám: $k$ és $n$, ezek értékét mindkét játékos ismeri. A játék megkezdésekor $A$ választ két egész számot: $x$-et és $N$-et, amikre $1\le x\le N$. $A$ az $x$ számot titokban tartja, viszont $N$-et őszintén megmondja $B$ -nek. $B$ ezután megpróbál $x$-re vonatkozó információt szerezni $A$-tól a következő típusú kérdésekkel: $B$ minden kérdésében megadja pozitív egész számok egy tetszőleges $S$ halmazát (olyan $S$ halmazt is megadhat, amit már korábban is megadott), és azt kérdezi $A$-tól, hogy $x$ eleme-e ennek az $S$ halmaznak. $B$ akárhány ilyen típusú kérdést feltehet. $A$-nak $B$ minden kérdésére a kérdés elhangzása után azonnal igennel vagy nemmel kell válaszolnia, de mindegyik válasza lehet hazugság is; az egyetlen kikötés az, hogy bármely egymás utáni $k+1$ válasz közül legalább egynek őszintének kell lennie. Miután $B$ annyiszor kérdezett, ahányszor csak akart, meg kell neveznie egy legfeljebb $n$ pozitív egész számból álló $X$ halmazt. Ha $x$ eleme az $X$ halmaznak, akkor $B$ nyer; különben $B$ veszít. Bizonyítsuk be: $1.$ Ha $n\ge 2^k$, akkor $B$-nek van nyerő stratégiája. $2.$ Minden elég nagy $k$-hoz van olyan $n\ge 1\mathrm{,}{99}^k$ egész szám, amire $B$-nek nincs nyerő stratégiája.   Janzer Olivér megoldása. 1. rész. Nyilván nem változik a feladat, ha az $\left\{\mathrm{1,2,}\text{...}\mathrm{,}N\right\}$ halmaz helyett tetszőleges $\left\{a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_N\right\}$ halmazból kerül ki $x$ ($a_i\ne a_j$). Ha $n\ge 2^k$, megmutatjuk a nyerő stratégiát. Ha $N\le 2^k$, akkor az $X=\left\{a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_N\right\}$ halmazra $|X|=N\le$ ≤2k≤n, így $|X|\le n$, tehát $X$ megfelelő, $B$ nyert. Tegyük fel, hogy $N>2^k$. $N$ szerinti teljes indukcióval bizonyítjuk be, hogy van nyerő stratégia. Tegyük fel, hogy $N=\ell$-re készen vagyunk (ahol $\ell \ge 2^k$). Bizonyítunk $N=\left(\ell +1\right)$-re. Kérdezzük meg az $S=\left\{a_1\right\}$ halmazt addig, amíg az első ,,igen'' választ nem kapjuk. Ha végig ,,nem''-et kapunk, még $k+1$ kérdés után is, akkor $x\ne a_1$ (hiszen ekkor a ,,nem'' igaz), így $x$ az $\ell$ elemszámú $\left\{a_2\mathrm{,}{a}_3\mathrm{,}\text{...}\mathrm{,}{a}_{\ell +1}\right\}$ halmazban van, így az indukciós feltétel szerint innen van nyerő stratégiánk. Tegyük fel egyébként, hogy a válasz egyszer ,,igen''. Rögtön ezután tegyük a következőt: vegyük az $a_2\mathrm{,}{a}_3\mathrm{,}\text{...}\mathrm{,}{a}_{2^k+1}$ számokat ($2^k+1\le \ell +1$). Rendeljük $a_j$-hez a $\left(j-2\right)$ sorszámot. Ekkor kiosztottunk sorszámokat 0-tól $\left(2^k-1\right)$-ig. Kódoljuk a sorszámokat 2-es számrendszerben. Ezután tegyünk fel $k$ darab kérdést, amelyek a következők: 1. $x$ benne van abban a halmazban, amely halmaz a kiválasztott számok közül azokat tartalmazza, amelyek sorszámának 2-es számrendszerbeli alakjában az első jegy 0? És így tovább, az $i$-edik kérdés a sorszám $i$-edik jegyére kérdez rá   (2-es számrendszerben). Így, mivel $2^k$ sorszámot osztottunk ki 0-tól $\left(2^k-1\right)$-ig és ezeket 2-es számrendszerben $k$ jegy kódolja: $\begin{array}{c}{\displaystyle 0:\underset{k}{\overset{}{\underbrace{00\text{...}0}}};1:\underset{k-1}{\overset{}{\underbrace{00\text{...}0}}}1;\text{...};2^k-1:\underset{k}{\overset{}{\underbrace{11\text{...}11}}}\mathrm{,}}\end{array}$ ezért $k$ kérdéssel $x$ sorszáma 2-es számrendszerbeli alakjának minden jegyére választ kapunk. Vegyük az utolsó $\left(k+1\right)$ darab feltett kérdésünket. Ezek között a feladat feltétele miatt lennie kell olyannak, amelyre $A$ őszintén válaszolt. Ekkor azonban kizárhatjuk az olyan $x$-eket, amelyekre az igaz válaszok mindig az $A$ által adott válaszok ellentétei. Belátjuk, hogy van ilyen szám. Az $A$ által adott első válasz ,,igen'', ennek ellentéte ,,nem'', továbbá a következő $k$ válasz tagadása meghatároz egy sorszámot, legyen ez $a_t$ sorszáma $\left(2\le t\le 2^k+1\right)$. Ekkor, mivel $a_1\ne a_t$, azért $x$ nem lehet $a_t$, ugyanis akkor az első kérdésre ,,nem'' az őszinte válasz, a további kérdésekre pedig $a_t$ definíciója szerint mindig az ellenkező, mint amit $A$ adott. Ez azonban ellentmond a feladat $\left(k+1\right)$ egymást követő kérdésre vonatkozó feltételének. Így $x\ne a_t$. Ekkor $x$ benne van egy $\ell$ elemű halmazban (az eredetiből elhagyjuk $a_t$-t), innen pedig az indukciós feltevés szerint van nyerő stratégiánk. Így a feladat első részének állítását igazoltuk.   2. rész. Megmutatjuk, hogy ha $1\mathrm{,}99<\lambda <2$ és $n=\left[\left(2-\lambda \right){\lambda }^{k+1}\right]-1$, valamint $N=n+1$, akkor $B$-nek nincs nyerő stratégiája. Jelöljük $V$-vel a $B$-nek azon kérdésére adott választ, hogy $x$ benne van-e az $S$ halmazban. Ekkor legyen $V$ inkonzisztens $i$-vel, ha a válasz ,,igen'' és $i$ nem eleme $S$-nek; vagy ha a válasz ,,nem'' és $i$ eleme $S$-nek. Legyen egy adott pillanatban $m_i$ az a szám, ami megadja, hogy $A$ addig (a legutolsót is beleértve) hány egymást követő, $i$-vel inkonzisztens választ adott. Például, ha a válaszok minősítése az $i$ szempontjából sorban ink.; nem ink.; ink.; ink., akkor éppen $m_i=2$. Legyen $\begin{array}{c}{\displaystyle \Phi =\sum _{i=1}^{n+1}{\lambda }^{m_i}\mathrm{.}}\end{array}$ Legyen $A$ válasza mindig olyan, hogy a válasza után a két lehetséges $\Phi$ érték közül a kisebbet kapjuk. Ehhez persze be kell látnunk, hogy ilyenkor $A$ lépései szabályosak. Elég azt megmutatnunk, hogy $\Phi <{\lambda }^{k+1}$, hiszen akkor mindegyik $m_i$ kisebb $\left(k+1\right)$-nél; viszont (legalább) $k+1$ egymást követő hazugság $k+1$ egymást követő inkonzisztens válasz lenne $x$-re nézve, amiből $m_x\ge k+1$ következne (a legalább $\left(k+1\right)$-edik inkonzisztens válasz után). Mindez azt jelenti, hogy a kívánt egyenlőtlenség mindenkori teljesülése esetén valóban nincs $k+1$ egymást követő hazugság, azaz $A$ válaszai szabályosak.   $\Phi <{\lambda }^{k+1}$ igazolása: Kezdetben $m_1=m_2=\text{...}=m_{n+1}=0$, így ${\Phi }_0=n+1$. Viszont $\begin{array}{c}{\displaystyle n+1=\left[\left(2-\lambda \right){\lambda }^{k+1}\right]\le \left(2-\lambda \right){\lambda }^{k+1}<{\lambda }^{k+1}}\end{array}$ (hiszen $\lambda >1$ miatt $2-\lambda <1$). Így kezdetben $\Phi <{\lambda }^{k+1}$. Tegyük fel, hogy valameddig $\Phi <{\lambda }^{k+1}$, majd vizsgáljuk a helyzetet $A$ aktuális válaszát követően. Ennek során $A$-nak két lehetséges válasza volt: ,,igen'', ami után ${\Phi }_1$ és ,,nem'', ami után ${\Phi }_2$ keletkezik. Mivel ő a kisebbet választotta, azért $\Phi \text{'}\le \frac{1}{2}\left({\Phi }_1+{\Phi }_2\right)$. Ha ezen kérdés az $S$ halmazra kérdez rá, és a válasz előtt $m_1\mathrm{,}{m}_2\mathrm{,}\text{...}\mathrm{,}{m}_{n+1}$ voltak a megfelelő értékek, akkor $\begin{array}{c}{\displaystyle {\Phi }_1=\sum _{i\in S}^{}{\lambda }^0+\sum _{j\notin S}^{}{\lambda }^{m_j+1}\text{és}{\Phi }_2=\sum _{i\in S}^{}{\lambda }^{m_i+1}+\sum _{j\notin S}^{}{\lambda }^0\mathrm{,}}\end{array}$ így ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \Phi \text{'}}& {\displaystyle \le \frac{1}{2}\left({\Phi }_1+{\Phi }_2\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\left({\sum }_{i\in S}\left({\lambda }^{m_i+1}+1\right)+{\sum }_{j\notin S}\left({\lambda }^{m_j+1}+1\right)\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\left(\left({\sum }_{i\in S}{\lambda }^{m_i+1}+{\sum }_{j\notin S}{\lambda }^{m_j+1}\right)+\left({\sum }_{i\in S}1+{\sum }_{j\notin S}1\right)\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\left({\sum }_{h=1}^{n+1}{\lambda }^{m_h+1}+{\sum }_{h=1}^{n+1}1\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\left(\lambda \Phi +n+1\right)\mathrm{.}}\hfill \end{array}}$ Mivel $\Phi <{\lambda }^{k+1}$ és $n+1=\left[\left(2-\lambda \right){\lambda }^{k+1}\right]\le \left(2-\lambda \right){\lambda }^{k+1}$, $\begin{array}{c}{\displaystyle \Phi \text{'}\le \frac{1}{2}\left(\lambda \Phi +n+1\right)<\frac{1}{2}\left({\lambda }^{k+2}+\left(2-\lambda \right){\lambda }^{k+1}\right)={\lambda }^{k+1}\mathrm{.}}\end{array}$ Tehát $\Phi$ nem lépi át ${\lambda }^{k+1}$-t. Így $A$ válaszai szabályosak. Viszont mivel ezek $x$-től függetlenek, $B$ nyilván nem találhatja ki $x$-et. Tehát ebben az esetben $B$-nek nincs nyerő stratégiája. Belátjuk, hogy elegendően nagy $k$ esetén $n$ megfelelő, azaz $\begin{array}{c}{\displaystyle n\ge 1\mathrm{,}{99}^k\cdot n=\left[\left(2-\lambda \right){\lambda }^{k+1}\right]-1.}\end{array}$ Először belátjuk, hogy $\begin{array}{c}{\displaystyle \left(2-\lambda \right){\lambda }^{k+1}\ge 1\mathrm{,}{99}^{k+1}\iff {\left(\frac{\lambda }{1\mathrm{,}99}\right)}^{k+1}>1/\left(2-\lambda \right)\mathrm{,}}\end{array}$ ami $\lambda >1\mathrm{,}99$ miatt nyilván igaz. Ekkor azonban (elég nagy $k$-ra) $\begin{array}{c}{\displaystyle n=\left[\left(2-\lambda \right){\lambda }^{k+1}\right]-1\ge \left(2-\lambda \right){\lambda }^{k+1}-2\ge 1\mathrm{,}{99}^k\mathrm{.}}\end{array}$ Ezzel a feladat állítását igazoltuk.     4. Határozzuk meg az összes olyan $f:\text{Z}\to \text{Z}$ függvényt, amire tetszőleges $a$, $b$, $c$ egészekre, amelyekre $a+b+c=0$ teljesül, fennáll az $\begin{array}{c}{\displaystyle f{\left(a\right)}^2+f{\left(b\right)}^2+f{\left(c\right)}^2=2f\left(a\right)f\left(b\right)+2f\left(b\right)f\left(c\right)+2f\left(c\right)f\left(a\right)}\end{array}$ egyenlőség. $(\text{Z}$ az egész számok halmazát jelöli.$)$   Nagy Róbert megoldása. A feltételt $a=b=c=0$-ra alkalmazva $3f{\left(0\right)}^2=6f{\left(0\right)}^2$, ebből $f\left(0\right)=0$. Legyen ezután $a=0$, $b=x$, $c=-x$, ekkor $f{\left(x\right)}^2+f{\left(-x\right)}^2=2f\left(x\right)f\left(-x\right)$, ebből pedig $f\left(x\right)=f\left(-x\right)$ adódik; tehát a függvény páros, így elég a függvényt csak a pozitív számokon megadni. A feladat feltételét pedig használhatjuk abban a formában (is), hogy ha $a$, $b$ és $c$ közül valamelyik a másik kettőnek az összege, akkor $\begin{array}{c}{\displaystyle f{\left(a\right)}^2+f{\left(b\right)}^2+f{\left(c\right)}^2=2f\left(a\right)f\left(b\right)+2f\left(b\right)f\left(c\right)+2f\left(c\right)f\left(a\right)}\end{array}$ teljesül. 1. eset: A függvénynek nincs más nullhelye. Jelöljük $f\left(1\right)$ értékét $d$-vel. Az $a=b=1$, $c=2$ választással $\begin{array}{c}{\displaystyle 2f{\left(1\right)}^2+f{\left(2\right)}^2=2f\left(1\right)f\left(1\right)+4f\left(2\right)f\left(1\right)\mathrm{.}}\end{array}$ Ebből $f\left(2\right)\ne 0$ miatt $f\left(2\right)=4f\left(1\right)=4d$. Ugyanígy $a=b=2$, $c=4$-ből $f\left(4\right)=16d$. Az $a=3$, $b=2$, $c=1$ választással $f\left(3\right)$-ra egy másodfokú egyenletet kapunk: $\begin{array}{c}{\displaystyle \left(f\left(3\right)-d\right)\left(f\left(3\right)-9d\right)=0.}\end{array}$ Ha itt $f\left(3\right)=d$, akkor $a=4$, $b=3$, $c=1$-ből ellentmondást kapunk, mert behelyettesítve az értékeket kapjuk, hogy $256d^2+d^2+d^2=32d^2+2d^2+32d^2$, ami lehetetlen. Tehát $f\left(3\right)=9d$, $f\left(4\right)=16d$. Innen teljes indukcióval bizonyítjuk, hogy $f\left(n\right)=n^{2}d$. Tegyük fel, hogy minden $0<k<n$-re teljesül, hogy $f\left(k\right)=k^{2}d$. Ebből $a=n$, $b=n-1$, $c=1$ választással $\begin{array}{c}{\displaystyle f{\left(n\right)}^2+f{\left(n-1\right)}^2+f{\left(1\right)}^2=2f\left(n\right)\left(f\left(n-1\right)+f\left(1\right)\right)+2f\left(1\right)f\left(n-1\right)\mathrm{,}}\end{array}$ $a=n$, $b=n-2$, $c=2$-vel pedig: $\begin{array}{c}{\displaystyle f{\left(n\right)}^2+f{\left(n-2\right)}^2+f{\left(2\right)}^2=2f\left(n\right)\left(f\left(n-2\right)+f\left(2\right)\right)+2f\left(2\right)f\left(n-2\right)\mathrm{.}}\end{array}$ A két egyenletet kivonva egymásból és behelyettesítve az ismert értékeket valóban azt kapjuk, hogy $f\left(n\right)=n^{2}d$. Ezzel az indukció teljes. Ha tehát nincs más nullhely, akkor $f\left(n\right)=n^{2}d$. 2. eset: Ha van más (pozitív) nullhely, akkor válasszuk ki a legkisebbet, legyen ez $a>0$, tehát $f\left(a\right)=0$. Minden $x$-re teljesül ‐ az $a=a$, $b=x$, $c=a+x$ választás miatt ‐ $\begin{array}{c}{\displaystyle f{\left(x\right)}^2+f{\left(a+x\right)}^2=2f\left(x\right)f\left(a+x\right)\mathrm{,}}\end{array}$ ezért $f\left(x\right)=f\left(a+x\right)$, tehát a függvény periodikus $a$ szerint. Így nyilvánvalóan minden nullhely osztható $a$-val, pontosabban: a nullhelyek éppen az $a$ többszörösei. Ezek után vizsgáljuk $a$ lehetséges értékeit. Ha $a\ge 5$, akkor az első eset bizonyítását megismételhetjük, mivel az csak $f\left(1\right)\mathrm{,}f\left(2\right)\mathrm{,}f\left(3\right)\mathrm{,}f\left(4\right)\ne 0$-ra alapult. Ezzel azt kapnánk, hogy más nullhely már nem lehet, ami ellentmondás; tehát $a\le 4$. Ha $a=4$, akkor $f\left(1\right)=d\ne \mathrm{0,}f\left(2\right)=4d$ és $\begin{array}{c}{\displaystyle f\left(3\right)=f\left(3-a\right)=f\left(-1\right)=f\left(1\right)=d\mathrm{.}}\end{array}$ Ha $a=3$, akkor $f\left(1\right)=d\ne \mathrm{0,}f\left(2\right)=4d$, de $f\left(1\right)=f\left(-1\right)=f\left(3-1\right)=4d$, ami ellentmondás. Ha $a=2$, akkor $f\left(1\right)=d\ne \mathrm{0,}f\left(2\right)=0$. Ha $a=1$, akkor $f$ a konstans 0 függvény. Könnyen ellenőrizhető, hogy a ki nem zárt függvények (minden $d\ne 0$-val) valamennyien megoldásai a feladatnak.     5. Legyen az $ABC$ háromszögben $BCA\sphericalangle ={90}^{\circ }$, és legyen $D$ a $C$-ből induló magasságvonal talppontja. Legyen $X$ a $CD$ szakasz belső pontja. Legyen $K$ az $AX$ szakasznak az a pontja, amire $BK=BC$. Hasonlóan, legyen $L$ a $BX$ szakasznak az a pontja, amire $AL=AC$. Legyen $M$ az $AL$ és $BK$ egyenesek metszéspontja. Bizonyítsuk be, hogy $MK=ML$.   Ódor Gergely megoldása. Az $A$ és $X$, $B$ és $X$, valamint $C$ és $D$ pontok által meghatározott egyeneseket nevezzük rendre $f$-nek, $e$-nek és $g$-nek. Húzzuk meg a $B$ középpontú, $\overline{BC}$ sugarú $k_1$ és az $A$ középpontú, $\overline{AC}$ sugarú $k_2$ köröket. A $g$ egyenes $k_1$ és $k_2$ hatványegyenese, mivel merőleges a körök $\overline{AB}$ centrálisára és átmegy az egyik metszésponton, $C$-n.   Tudjuk, hogy a $k_1$ körnek az $f$ egyenessel való, $A$-hoz közelebbi metszéspontja $K$. A másik metszéspontot nevezzük $Q$-nak. Hasonlóan a $k_2$ kör és az $e$ egyenes $B$-hez közelebbi metszéspontja $L$, a másikat pedig jelölje $P$. 1. állítás: $XPK▵\sim XQL▵$. Bizonyítás: Mivel $X$ a hatványegyenes egyik pontja, $\begin{array}{c}{\displaystyle \overline{XK}\cdot \overline{XQ}=\overline{XL}\cdot \overline{XP}\mathrm{.}}\end{array}$ Átalakítva $\begin{array}{c}{\displaystyle \frac{\overline{XK}}{\overline{XP}}=\frac{\overline{XL}}{\overline{XQ}}\mathrm{.}}\end{array}$ Az $XPK$ és $XQL$ háromszögek két oldalának aránya és az oldalak által bezárt szög (csúcsszögek miatt) megegyezik. Tehát $XPK▵\sim XQL▵$. Következmény: A $KPQL$ négyszög húrnégyszög, mert $\begin{array}{c}{\displaystyle PLQ\sphericalangle =PKQ\sphericalangle \mathrm{.}}\end{array}$ A $KPQL$ körülírt körét jelölje $k_3$, középpontját pedig $O$. 2. állítás: Az $AL$ egyenes érinti $k_3$-at. Bizonyítás: $\overline{AC}\perp \overline{BC}$ és $\overline{BC}$ a $k_1$ kör   sugara, tehát $A$-nak a $k_1$ körre vonatkozó hatványa $={\overline{AC}}^2$. Mivel $A$ rajta van a $QK$ egyenesen, rajta van $k_1$ és $k_3$ hatványegyenesén. Ebből következik, hogy a $k_3$ körre vonatkozó hatványa is $\begin{array}{c}{\displaystyle {\overline{AC}}^2={\overline{AL}}^2\mathrm{.}}\end{array}$ Tehát az $A$-ból $k_3$-hoz húzott érintő szakaszok hossza $\overline{AL}$. A $k_3$ körön legfeljebb két olyan pont lehet, amely $A$-tól $\overline{AL}$ távolságra van. Mivel $P$ és $L$ ilyen és e körhöz $A$-ból két érintő húzható, mindkét pont érintési pont. ($A$ kívül esik a $k_3$ körön, mivel rajta van a hatványvonalon és kívül van a $k_1$ körön, hiszen $\overline{AB}>\overline{BC}$). Hasonlóan látható be a 3. állítás: A $BK$ egyenes érinti $k_3$-at. Mivel $\overline{ML}$ és $\overline{MK}$ a $k_3$ körhöz húzott érintő szakaszok, egyenlő hosszúak. Ezzel igazoltuk a feladat állítását.     6. Határozzuk meg az összes olyan $n$ pozitív egész számot, amelyhez találhatók olyan $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_n$ nemnegatív egészek, amelyekre teljesül $\begin{array}{c}{\displaystyle \frac{1}{2^{a_1}}+\frac{1}{2^{a_2}}+\text{...}+\frac{1}{2^{a_n}}=\frac{1}{3^{a_1}}+\frac{2}{3^{a_2}}+\text{...}+\frac{n}{3^{a_n}}=1.}\end{array}$   Strenner Péter megoldása. Azt fogjuk bizonyítani, hogy akkor és csak akkor léteznek megfelelő $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_n$ nemnegatív egészek, ha $n\equiv \mathrm{1,2}\left(\text{mod 4}\right)$. A feltétel szükséges voltának igazolásához hozzuk közös nevezőre az $\begin{array}{c}{\displaystyle 1=\frac{1}{3^{a_1}}+\frac{1}{3^{a_2}}+\text{...}+\frac{1}{3^{a_n}}}\end{array}$   összeget: megfelelő $b_0\mathrm{,}{b}_1\mathrm{,}\text{...}\mathrm{,}{b}_n$ egészekre $\begin{array}{c}{\displaystyle 1=\frac{3^{b_1}+2\cdot 3^{b_2}+\text{...}+n\cdot 3^{b_n}}{3^{b_0}}\mathrm{.}}\end{array}$ Elég észrevenni, hogy $i$ és $i\cdot 3^{b_i}$ paritása azonos, így az $1+2+\text{...}+n=\frac{n\left(n+1\right)}{2}$ összeg páratlan. Ez valóban azt vonja maga után, hogy $n\equiv \mathrm{1,2}\left(\text{mod 4}\right)$. Legyen $S$ az egész számokból álló végtelen sorozatok halmaza, és legyen azon értelmezett két függvény: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle f}& {\displaystyle :S\to \text{R}\mathrm{,}f:\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\right)\to {\sum }_{a_i\ge \mathrm{0,}i\in N}\frac{1}{2^{a_i}}\mathrm{,}}\hfill \\ \hfill {\displaystyle g}& {\displaystyle :S\to \text{R}\mathrm{,}g:\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\right)\to {\sum }_{a_i\ge \mathrm{0,}i\in N}\frac{i}{3^{a_i}}\mathrm{.}}\hfill \end{array}}$ Az $s=\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\right)\in S$ sorozat jó, ha van olyan $n$ pozitív egész szám, amelyre $a_i\ge 0\iff i\le n$ és $f\left(s\right)=g\left(s\right)=1$. Azt kell tehát bizonyítani, hogy minden $n\equiv \mathrm{1,2}\left(\text{mod 4}\right)$ esetén létezik jó sorozat. Teljes indukciót alkalmazunk. Tegyük fel, hogy egy $n\ge 12$ egészhez található egy jó $s=\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\right)$ sorozat. Belátjuk, hogy ebből konstruálható egy jó sorozat $n+12$-re a következő kétféle módosítás segítségével: 1. ha az $s=\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\right)\in S$ sorozatban $a_k\ge 0$, de $a_{2k}<0$, akkor $f\left(s\right)=f\left(s\text{'}\right)$ és $g\left(s\right)=g\left(s\text{'}\right)$, ahol $s\text{'}=\left(b_1\mathrm{,}{b}_2\mathrm{,}\text{...}\right)$, $a_i=b_i$, ha $i\ne k\mathrm{,2}k$, $b_k=b_{2k}=a_k+1$. 2. ha az $s=\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\right)\in S$ sorozatban $a_k\ge 0$, de $a_{\ell }\mathrm{,}{a}_m<0$, és $3k=\ell +m$, akkor $f\left(s\right)=f\left(s\text{'}\right)$ és $g\left(s\right)=g\left(s\text{'}\right)$, ahol $s\text{'}=\left(b_1\mathrm{,}{b}_2\mathrm{,}\text{...}\right)$, $a_i=b_i$, ha $i\ne k\mathrm{,}\ell \mathrm{,}m$, $b_k<0$, $b_{\ell }=b_m=a_k+1$. Feltéve, hogy $n$-re létezik jó $s$ sorozat, vagyis $f\left(s\right)=g\left(s\right)=1$, a fenti kétféle módosításokkal kapott $s\text{'}$ sorozatra is $f\left(s\text{'}\right)=g\left(s\text{'}\right)=1$. Emiatt már csak azt kell garantálni, hogy $s\text{'}$-ben az első $n+12$-nél nem nagyobb indexű tagok nemnegatívak, az összes többi pedig negatív legyen. Mivel feltettük, hogy $n\ge 12$, az $a_{n+1}\mathrm{,}\text{...}\mathrm{,}{a}_{n+12}$ tagok közül a páros indexűeket 1-es típusú lépésekkel nemnegatívba tudjuk vinni. Ezután a 6 db páratlan indexű tag párokba rendezhető úgy, hogy a párosított tagok indexeinek összege osztható 12-vel, hiszen az indexek 12-es maradéka 1, 3, 5, 7, 9, 11 valamilyen sorrendben. Ezeket a párokat a 2-es típusú lépést alkalmazva tudjuk nemnegatívvá tenni. Ha egy ilyen lépés eredményeképpen az $a_{\ell }$ és az $a_m$ tag vált nemnegatívvá, akkor a (páros indexű) $a_{\frac{\ell +m}{3}}$ tag negatívvá változik, amit egy 1-es típusú átalakítással újra nemnegatívba tudunk vinni. Végül megadunk egy-egy megfelelő $\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_n\right)$ sorozatot $n$ kis értékei esetén: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|cc|}\hline {\displaystyle n=1}\hfill & {\displaystyle \left(\mathrm{0,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=2}\hfill & {\displaystyle \left(\mathrm{1,1,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=5}\hfill & {\displaystyle \left(\mathrm{2,1,3,4,4,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=6}\hfill & {\displaystyle \left(\mathrm{2,1,3,5,5,4,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=9}\hfill & {\displaystyle \left(\mathrm{2,1,3,7,5,4,8,8,6,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=10}\hfill & {\displaystyle \left(\mathrm{2,1,3,7,6,4,8,8,6,6,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=13}\hfill & {\displaystyle \left(\mathrm{1,4,5,5,5,6,4,5,4,5,4,6,4,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=14}\hfill & {\displaystyle \left(\mathrm{1,4,5,5,5,6,5,5,4,5,4,6,4,5,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=17}\hfill & {\displaystyle \left(\mathrm{2,1,5,6,6,5,7,6,7,6,6,5,6,7,7,6,6,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=18}\hfill & {\displaystyle \left(\mathrm{2,1,5,6,6,5,7,6,8,6,6,5,6,7,7,6,6,8,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=21}\hfill & {\displaystyle \left(\mathrm{2,1,3,8,6,7,9,8,7,7,10,7,10,9,6,9,7,7,7,7,6,}\text{...}\right)\mathrm{,}}\hfill \\ {\displaystyle n=22}\hfill & {\displaystyle \left(\mathrm{2,1,3,8,6,7,9,8,7,7,11,7,10,9,6,9,7,7,7,7,6,11,}\text{...}\right)\mathrm{,}}\hfill \\ \hline\end{array}}}\end{array}$ Ezzel a teljes indukció elvének megfelelően az állítás bizonyított.