Cím: Konferenciaközpont építése avagy felületek háromszögelése
Szerző(k):  Makay Géza 
Füzet: 2011/szeptember, 329 - 335. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Konferenciaközpont építése

avagy

Felületek háromszögelése

 
A feladat
 
A szegedi székhelyű Alukonstrukt Kft. többek között fémből készült merevítő rudakból épít olyan felületeket, amelyeknek a lapjait háromszög alakú üveglapok alkotják. Az ilyen felületek megkonstruálása komoly mérnöki kihívás, hiszen figyelembe kell venni a felület önsúlyán kívül a szélnyomást, a hóterhet, az esetleges földmozgások hatását stb. Kimerítő irodalma van a megszokottabb formájú kupolák és felületek kialakításának, mint például a hengerpalást és a gömbcikk, és sok olyan mérnöki szoftver is létezik, amelyet alapvetően ilyen felületek megkonstruálásához alkottak.
Manapság már szokatlanabb formákkal is kísérleteznek az épületeket megálmodó művészek és tervezők (lásd a hátsó belső borítót). Az ilyen felületek megépítéséhez megfelelő geometria kialakítása (háromszögelése) már nehéz probléma, nem is szólva az ezzel kapcsolatos további mérnöki feladatokról.
2009 végén az Alukonstrukt Kft. egy matematikai és programozási problémával kereste meg a Szegedi Tudományegyetem Bolyai Intézetét (Matematikai Tanszékcsoportját). A feladat egy megadott, nem (feltétlenül) szabályos felülethez olyan háromszögeléseket keresni, amelyeket az erre a célra megírt tervező szoftverekkel tovább elemezve és módosítva megkonstruálható legyen egy, a gyakorlatban is megépíthető fém-üveg épület. A kialakítandó háromszögeléseknek meg kell felelniük többek között a következő feltételeknek:
1. A felület belsejében a csúcspontok csak 5-öd vagy 6-odfokúak lehetnek. Más fokszámok esetén nehezen lehetne kialakítani az élek csatlakozó elemeit, illetve túl kicsi fokszám esetén a felület nem lenne elég strapabíró, túl nagy fokszám esetén pedig nagyon hegyes szögeket kapnánk, amit nehezen lehet kialakítani üvegből.
2. Az élek hosszának előre adott abszolút minimális és maximális hossz közé kell esnie, illetve meg van adva egy elvárt minimális és maximális hossz is. Az elvárt élhossz általában 120 és 220 cm között szokott lenni, ez az élhossz éppen megfelelő ahhoz, hogy az ezek által határolt üveg háromszöglapok kezelhetőek legyenek.
3. A háromszögek szögei nagyságának előre adott abszolút minimális és maximális érték közé kell esnie, illetve meg van adva egy elvárt minimális és maximális nagyság is. Itt az abszolút határok 40∘ és 95∘ szoktak lenni: például bejáratok sarkainál levő 90∘ szöget vagy nem osztjuk fel kettőre, és 90∘-os szöget kapunk, vagy felosztjuk, és akkor 45∘-osak lesznek a részei. Az elvárt határok persze nyilván a 60∘ és 72∘, hiszen hatod- és ötödfokú csúcsoknál ilyen szögek jönnek elő.
4. A felületen görbék vannak megadva (például a felület pereme, bejáratok oldalai és teteje, vagy a felületen belül egy támaszfal vonala), ezeket a generált háromszögeléseknek követniük kell.
5. A felületen továbbá rögzített csomópontok is meg vannak adva (például bejáratok sarkai, alátámasztási pontok, mint például egy tartóoszlop teteje), ezeknek a csúcspontoknak azért kell szerepelniük a háromszögelésekben, mert az egész épületnek alapvető, építészeti szempontból fontos részei.
Természetesen ezek a feltételek még nem elegendőek ahhoz, hogy a felület a gyakorlatban is megépíthető legyen, de az ezen feltételeket nem teljesítő felületek nem, vagy csak nehezen konstruálhatóak meg. A megírandó programnak felhasználóbarátnak, könnyen használhatónak és természetesen eredményesnek kell lennie:
1. A program képes legyen a mérnöki szoftverekben használatos egyik formátumból (DXF = Drawing Interchange Format) beolvasni és ugyanebbe a formátumba kiírni a felület, a rögzített élek és csúcsok adatait, valamint (a továbbfeldolgozást megkönnyítendő) a felület normálvektorait a csúcspontokban és az élek felezőpontjaiban.
2. A beimportált és a generált háromszögeléseket perspektivikusan, vonalas és árnyalt (takarásos) ábrázolásban, szórt fényben és ú.n. spotlámpa (egy adott pontból történő) megvilágításban is meg kell jeleníteni, az ellenőrzés kedvéért akár hamis színekben is, ahonnan kitűnnek a problémás felületdarabok. Az ábrázolás nagyítható, mozgatható és forgatható, a perspektíva pedig változtatható kell legyen, hogy a felületet bármilyen szögből és szempontból meg tudjuk vizsgálni.
3. A háromszögeléshez használt paraméterek beállítása után a generált háromszögelésekről a program készítsen statisztikát: minimális és maximális élhossz, az élhosszak átlaga és szórása, minimális és maximális szögméret, a szögek átlaga (mindig 60∘) és szórása, a csúcsok, élek és lapok száma, a fokszámok minimuma és maximuma a felület belsejében és a felület határán. Ez alapján a hozzáértő felhasználó ki tudja választani azt a néhány háromszögelést, amelyekkel érdemes a továbbiakban foglalkozni.
4. Az éppen vizsgált háromszögelés legyen szerkeszthető: lehessen éleket, csúcsokat és lapokat törölni, új éleket, csúcsokat és lapokat létrehozni, és a kialakult háromszögelést simítani (vagyis a csúcsokat automatikusan úgy elmozgatni a felületen, hogy az jobban megfeleljen az élekre és szögekre tett feltételeknek). Ezzel a program automatikus, de a felhasználó szemszögéből nézve nem megfelelő háromszögei javíthatóak.
 

Az alapvető algoritmus
 
Az irodalomban kevés az általános felületek háromszögelésére vonatkozó cikk. Ezek többsége is általában a fentiek közül csak kevés (általában egy) szempontra koncentrál, és nem találunk olyan eredményt, amelyik a csúcsok fokszámaival foglalkozna. Így egy olyan algoritmust kellett kitalálni, amelyik ezen feltételek mindegyikének igyekszik megfelelni. Vizsgáljuk meg a problémát ilyen szempontból, és próbáljuk meg kidolgozni a megoldáshoz szükséges alapvető módszereket.
A felület a 3 dimenziós térben van. Nyilvánvalóan 3 dimenziós koordinátageometriát kell használni a csúcspontok helyzetének tárolására. Két ilyen csúcs meghatároz egy élt, három páronként éllel összekötött csúcspont pedig egy háromszöglapot.
A felületet háromszögelt formában kapjuk meg. Ez azt jelenti, hogy az eredeti, ki tudja milyen módon (például függvénygrafikonnal, transzformációkkal stb.) megadott felület már átesett egy olyan átalakításon (a háromszögelésen), amelyik rontott rajta. Első kérdés, hogy ezek után mi legyen az a felület, amit háromszögelnünk kell. Nyilvánvalóan nem az a poliéder-darab, amit így kapunk, hiszen az már ,,el van rontva'', ki kell simítani az abban a háromszögelés miatt keletkezett sarkokat. Ezt a következő módszerrel tehetjük meg: az összes háromszöglapot felbontjuk 4 háromszögre az oldalfelező pontok összekötésével, és az újonnan keletkezett pontokat úgy mozgatjuk, hogy az egymástól nem túl távol eső lapok által bezárt szögek ne térjenek el túlzottan egymástól. Eközben persze figyelnünk kell rá, hogy a rögzített élek mentén keletkező csúcsokat úgy mozgassuk el, hogy a rögzített él megmaradjon: ezt úgy érjük el, hogy ezeket a csúcsokat a rögzített él síkjában fogjuk mozgatni, míg a többit a felületre merőlegesen. Ezt a finomításnak nevezett műveletet egymás után többször is végrehajtva kaphatunk egy olyan elég finom háromszögelést, ami már jól fogja közelíteni az eredeti felületet. Egy másik előnye a finomításnak, hogy a majdan keletkező háromszögelés csúcsai ezen finomítás csúcsai közül fognak kikerülni. Tehát az, hogy a keletkező háromszögelés csúcsai a felületen legyenek, ne csússzanak le a felületről az egyes csúcsok sokszori mozgatásával sem, ezzel a trükkel könnyedén biztosítható.
Ezek után a probléma úgy merül fel, hogy mely csúcsokat kell kiválasztani a finomított felületből, és azokat hogyan kell élekkel összekötni, hogy megfelelő háromszögelést kapjunk. Többféle módszer is lehetséges ‐ legtöbbjük azon alapul, hogy valamilyen módon egyenletesen osszuk el a felületen a pontokat (például úgy, hogy a pontok közötti távolságok minimumát maximalizáljuk), és azután az így kialakuló pontokra illesztünk éleket és lapokat a feltételeknek megfelelően. Ezek a módszerek nem sikeresek: nagyon nehezen, vagy éppenséggel egyáltalán nem betartható, hogy a felület belsejében a csúcsok fokszáma csak 5 és 6 legyen. Éppen ezért végül a programba beépített módszer az volt, hogy a felületet háromszögenként építjük fel úgy, hogy közben mindig betartjuk a fokszám-feltételt. Eközben vigyázunk rá, hogy a rögzített csúcsokat felvegyük a háromszögelésbe. Emellett rögzített éleken is csak akkor lép át az algoritmus, ha már nem tud más módon új háromszöget létrehozni; ezzel biztosítjuk, hogy a rögzített élek is megmaradjanak. Az újabb háromszögek felvétele után a felületet simítjuk, mozgatjuk a csúcsait úgy, hogy azok jobban megfeleljenek az élhosszakra és a szögnagyságokra tett feltételeknek.
 
Matematikai módszerek és felhasznált tételek
 
Ami a legmeglepőbb, hogy nem szükséges magasabb matematika a feladat megoldásához. Minden felhasznált matematikai módszer középiskolából ismert vagy elmondható az ottani ismeretekre építve.
Először is felhasználjuk az Euler-féle poliédertételt, miszerint ha egy poliédernek c csúcsa, l lapja és e éle van, akkor c+l=e+2. Ebből levezethető egy nagyon furcsának, és első látásra hihetetlennek tűnő
Állítás. Ha egy háromszögekből álló poliédernek csak 5-öd és 6-odfokú csúcsai vannak, akkor pontosan 12db 5-ödfokú csúcsa van.
Bizonyítás. Legyen az 5-ödfokú csúcsok száma c5, a 6-odfokúaké c6, így c=c5+c6. Számoljuk össze kétféleképpen az élek számát. Ha összeadjuk a csúcsok fokszámait, akkor minden élt kétszer számoltunk, hiszen egy élnek két vége van, így 5c5+6c6=2e. Másrészt a lapoknak 3 élük van, a lapok számának háromszorosa megint az élek számának kétszeresével kell megegyezzen, hiszen egy élt ismét két laphoz számolunk hozzá: 3l=2e. Ezekhez vegyük még hozzá az Euler-féle poliédertételt, és a következő egyenletrendszert kapjuk:
5c5+6c6=2e,(1)
 
3l=2e,(2)
 
c5+c6+l=e+2.(3)
Az utolsó egyenlőség 6-szorosából vonjuk ki az első egyenlőséget és a második 2-szeresét, így kapjuk, hogy c5=12, és ezzel beláttuk az állítást. A probléma szempontjából lényegtelen, de egy matematikus fejében persze felmerül a kérdés, hogy hány 6-odfokú csúcs lehet. Kiderül, hogy 1 db 6-odfokú csúcs nem lehetséges, bármilyen más darabszám előfordulhat.
Nézzünk erre az állításra egy példát. Az ikozaéder egy 20 háromszöglapot tartalmazó test, amelynek mind a 12 csúcsa 5-ödfokú. Ha erre a poliéderre alkalmazzuk a fenti finomítás módszerét, akkor az újonnan keletkező csúcsok fokszáma mindig 6 lesz. A finomítás akármennyiszer alkalmazható, úgyhogy 6-odfokú csúcsból akármilyen sok lehet, de 5-ödfokúból mindig pontosan 12 db lesz.
Ebből az állításból derült ki, hogy a feladatban megfogalmazott feltételek közül a fokszámokra vonatkozó a legerősebb. Az eredeti problémában nem teljes poliéderfelületről van szó, egy poliéderből kimarad egy vagy több (nem feltétlenül háromszög alakú) lap, de ez az Euler-féle poliédertételen csak minimális mértékben változtat (c+l+d=e+2, ahol d a kimaradó lapok száma) és ha tartani akarjuk az élek hosszára vonatkozó feltételt, akkor az 5-ödfokú csúcsokra is csak annyit jelent, hogy azok száma legfeljebb 12. A feltételeknek megfelelően háromszögelhető felület, amit keresünk, egy lényegében konvex 3 dimenziós test felületének egy darabja kell legyen.
 
A megjelenítés
 
A vektorok hossza és a skaláris szorzat segítségével ki tudjuk számolni az élek hosszát és a háromszöglapok szögeit. Így a háromszögelés simításakor a következő eljárást tudjuk követni:
• Számoljuk ki egy adott csúcspont esetén a csúcspontból induló élek hosszának az elvárttól való eltérésének az átlagát.
• Ugyancsak számoljuk ki a csúcspontnál levő lapok szögeinek a 60∘-tól való eltérésének az átlagát.
• Az így kapott számok súlyozott összegét megpróbáljuk csökkenteni azáltal, hogy a csúcsot átmozgatjuk a finomított felületen ezzel a csúccsal szomszédos másik csúcspontba.
• Amíg ez megtehető, addig folytatjuk ezt az eljárást; minden csúcsra addig ismételjük, amíg tudunk csúcspontot mozgatni.
Ez az eljárás megkeresi a fenti súlyozott összegnek egy minimális értékét az adott háromszögelésre, próbálja csökkenteni az élhosszak és a szögnagyságok eltéréseit: a felület háromszögelése ,,szebb'' lesz.
Ha egy lap két élének vektorát vektoriálisan összeszorozzuk, és a kapott vektort normáljuk (elosztjuk a hosszával), akkor megkapjuk a lap normálvektorát. Egy él normálvektorát úgy kapjuk, hogy az élre illeszkedő lapok normálvektorainak összegét normáljuk. A csúcspont normálvektorát úgy kapjuk, hogy a csúcspontban levő lapok normálvektorainak összegét normáljuk. A normálvektorokat úgy határozzuk meg, hogy a felületből kifelé mutassanak. Hogy egységes legyen, milyen irányba mutatnak a normálvektorok, először rögzítjük egy háromszög normálvektorát, ez megmutatja, hogy melyik irányban van a felület külső része, és a csatlakozó háromszögek normálvektorait ez alapján már be tudjuk állítani.
Hogyan lehet egy spotlámpa megvilágítását kiszámolni egy felületre? Ha a spotlámpa merőlegesen világít a felületre, akkor világítja meg leginkább. Minél nagyobb a normális és a spotlámpát a háromszög súlypontjával összekötő vektor szöge, annál kevésbé világítja meg a spotlámpa a háromszöget, és ha ez a szög 90∘-nál nagyobb, akkor a spotlámpa egyáltalán nem világítja meg a felület külsejét. Ezt a szöget skaláris szorzattal egyszerűen ki tudjuk számolni. A programban meg van adva két szín: a szórt fény (általában) viszonylag sötét színe és a teljes megvilágítás világosabb színe. A szög (vagy több spotlámpa esetén szögek) alapján a két szín egy súlyozott átlagát számolja ki a program, és ezzel a színnel rajzolja ki a háromszög perspektív képét.
A probléma matematikai szempontból egyik nehezebb része: hogyan rajzoljuk ki a perspektivikus ábrát, és hogyan oldjuk meg a láthatóságot (takarást)? Először az utóbbira válaszolunk. A 3 dimenziós tér egy adott pontjából nézzük a felületet. A lapokat rakjuk sorrendbe a súlypontjuknak ettől a ponttól vett távolsága szerint. Először a legtávolabbi lapot kirajzolva és közeledve a nézőponthoz a közelebbi lapok teljesen természetesen eltakarják a távolabbiakat. A lapokra illeszkedő éleket és csúcsokat a lapokkal együtt rajzoljuk ki, így nem lehet gond azok takarásával sem. Ez az algoritmus a cikkben szereplő felületekre jó, de lehet olyan felületet konstruálni, amelyre nem megfelelő, sőt, olyan felület is van, ahol nem lehet a háromszögek olyan sorrendjét felállítani, amilyen sorrendben azokat kirajzolva a perspektívának megfelelő ábrát kapnánk. Viszont a feladat megoldása során az algoritmus gyorsasága is lényeges, egy pontosabb algoritmusnak sokkal nagyobb lenne az időigénye.
A nézőponton (ahonnan nézzük: q) kívül van egy ettől különböző nézett pont is (ahová nézünk: v), ez meghatározza a nézési irányt, legyen ez az n→, ami a v-q vektor normáltja. Vigyázzunk rá, hogy a nézési irány a forgatás és mozgatás következményeként se lehessen függőleges. Így ha az ember (szokása szerint) vízszintesen tartja a fejét, akkor meg tudjuk határozni, hogy merre van a jobbra irány (j→); ez a 3 dimenziós vektor teljesíti következő feltételeket: merőleges a nézési irányra, a z komponense 0, és egységvektor. Ez egy egyszerű lineáris egyenletrendszer megoldását jelenti. A nézési és jobbra irányból pedig vektoriális szorzattal megkapható a felfelé irány (f→), tehát hogy mennyire billentjük a fejünket előre vagy hátra. Az egészet úgy kell elképzelni, hogy egy az n→-ra merőleges sík van a nézőponttól 1 egységnyi távolságra, amelynek vízszintes tengelye j→, függőleges tengelye pedig f→, és a vetület nem más, mint a nézőpontot a vetített ponttal összekötő egyenes és a sík metszéspontja a j→ és f→ vektorok lineáris kombinációjaként kifejezve (ld. az 1. ábrát).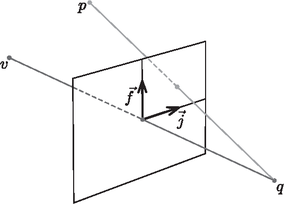
 
 
1. ábra
 

Tehát, először is ellenőrizzük, hogy a pontot látjuk-e, előttünk van-e: (p-q)⋅n→>0. Ha igen, akkor a pont perspektivikus vetülete
((p-q)⋅j→,(p-q)⋅f→)/((p-q)⋅n→).

Ez a képlet a nézett pontot a (0,0) 2 dimenziós vektorba vetíti; persze ezt a képletet módosítani kell úgy, hogy ezt a pontot egy lineáris transzformációval eltoljuk a képernyő közepére és kinagyítjuk a képernyő felbontásának és persze a felhasználó utasításainak megfelelően.
A perspektívát a nézőpont (q) nézett ponthoz való közelítése, illetve távolítása változtatja. A felület forgatása nem más, mint a nézőpont (q) változtatása, a felület mozgatása pedig a nézett pont (v) változtatásával oldható meg, de persze mindkettő úgy, hogy q és v távolsága közben ne változzon. Így most már meg tudunk jeleníteni háromszögekből álló felületeket mindenféle szögből és perspektívában.
A háromszögelés

Eljutottunk a feladat lényegéhez: hogyan háromszögeljünk egy (elég sok finomítás után) sűrű háromszögráccsal megadott felületet a feltételeknek megfelelően? Azt már tudjuk, hogy a fő lépés az újabb háromszögek felvétele úgy, hogy a fokszámokra tett kikötést közben betartsuk, az élekre és szögekre tett megszorításokat pedig simításokkal próbáljuk kielégíteni. Kiindulunk tehát egy pontból, és konstruálunk egy olyan háromszöget, amelynek ez az egyik csúcsa. Így a felület egy darabját már lefedtük háromszöggel. Ennek a háromszögnek vannak ,,külső'' élei, tehát olyan élek, amelyeken túl még folytatódik a felület. Egy ilyen külső élre konstruálunk egy újabb háromszöget, és ezt folytatjuk mindaddig, amíg végül minden él már az eredeti felület határán lesz, és akkor kész a háromszögelés. De a fő kérdés megmarad: hogyan veszünk hozzá újabb háromszögeket egy meglevő háromszögrácshoz?
Több szempontot kell figyelembe vennünk. Egy csúcs legalább 5-öd, és legfeljebb 6-odfokú lehet. Ezért egy 6-odfokú (tehát már hat él végpontjaként szereplő) csúcshoz nem vehetünk hozzá újabb éleket, a meglevő élek végpontjait megfelelő sorrendben (!) összekötve ez a csúcspont az új háromszögelés belső csúcspontja lesz, és a továbbiakban (a simítást kivéve) nem foglalkozunk vele (2. ábra).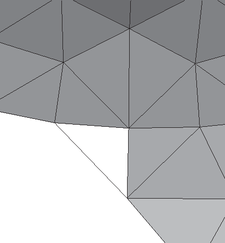

 
2. ábra. A berajzolt élt be kell húzni, hogy a csúcspont 6-odfokú maradjon
 

 
3. ábra. Az ABC és a BDE háromszögek átfedőek

Minden más esetben keresünk egy megfelelő külső élt, és konstruálunk rá egy háromszöget a következőket figyelembe véve. A háromszögeknek egyszeresen kell lefedniük a felületet, tehát nem szabad, hogy kialakuljon például a 3. ábrán látható átfedéses helyzet.
Ehhez az kell, hogy egy külső élhez hozzáveendő új csúcs (ami a külső éllel együtt alkotja majd az új háromszöget) olyan kell legyen, amelyik a külső él két végpontjánál nem az addig megkapott háromszögek által ,,lefedett'' felületdarabra esik. Ez egy kicsit homályos megfogalmazás, hiszen a felület a jóval finomabb háromszögelés miatt görbül, és így általában nem esik egybe egyetlen, az új háromszögelésben szereplő háromszög síkjával sem, és mégis ezt valahogy ellenőrizni kellene. Erre a következő eljárás megfelelő: a külső él mindkét végpontjára végrehajtjuk az alábbi számítást. A csúcspontban veszünk egy, a normálisra merőleges síkot, a felület érintősíkját. Erre merőlegesen vetítjük a végpontot tartalmazó háromszögeket, illetve az újonnan felveendő csúcspontot. Ha az él végpontját az új csúcsponttal összekötő félegyenes vetülete erre a síkra belemetsz bármelyik így vetített háromszögbe, akkor az a csúcspont nem lesz megfelelő (ld. az 5. ábrát).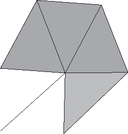
 
4. ábra. Helyes új csúcspont
 
 
5. ábra. Helytelen új csúcspont

A merőleges vetületek, illetve az egyenes és háromszögek metszetének kiszámolására ismét csak a skaláris szorzatot használhatjuk.
A program ismertetése során nem szóltunk a háromszögrács javításáról (ez a megfelelő adatstruktúrák megfelelő kezelésén múlik), a rögzített élek és csúcsok megtartásáról (a simításnál az új háromszögelés egyszerűen ráfeszül ezekre), a finomításnál az újonnan felvett csúcspontok mozgatásáról stb. Ezek programozástechnikai problémák. Ugye nem volt nehéz a felületek háromszögelésének elmélete?