Cím: 51. Rátz László Vándorgyűlés
Szerző(k):  Miklós Ildikó 
Füzet: 2011/szeptember, 325 - 328. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A matematikatanárok idén a szlovákiai Révkomáromba, vagy ahogy lakói újabban nevezik (és ezt az elnevezést a köztudatba is szeretnék átvinni), Észak-Komáromba vándoroltak. Ezzel első ízben lépte át a vándorgyűlés a határt, igaz, csak egy pár méterrel. A helyszín a 2004-ben létesült, magyar oktatási nyelvű Selye János Egyetem Konferencia-központja volt.
A megnyitón hagyományosan kiosztották a Beke Manó Emlékdíjakat, majd előadást hallgathattunk meg Berzsenyi Györgytől az általa szervezett amerikai tehetséggondozásról1, majd a tavalyi Rátz Tanár Úr Életműdíjas Deli Lajostól és Somfai Zsuzsától, akik tanári pályájukról meséltek. Az előadások után következett a kulturális program, amelyben a komáromi Selye János Gimnázium három diákja adott ízelítőt tehetségéből: Bertók Tibor hegedűn játszott, Habodász István szavalt, Szurcsík Ádám énekelt, mindhárman nagy sikerrel.
Szokásosan délelőttönként zajlottak az előadások és a feladatmegoldó szemináriumok. Szerda délután fórumok, bemutatók mellett zajlott a tanárverseny, amelynek feladatait és az eredményeket külön közöljük. A versenyt a TypoTeX Kiadó, a Maxim Kiadó és a Mategye Alapítvány támogatta. Szintén szerda délután zajlott a hagyományos Budapest‐Vidék focimeccs (idén Budapest győzelmével) és a női kosárlabdameccs is. Ez utóbbiban vegyes csapatok alakultak, mindkét oldalon voltak budapestiek is, vidékiek is, de az tény, hogy az egyik (többségében vidékiekből álló) csapat nyert. Csütörtök délután három helyszínre kirándultunk.
Az előadások anyagai megtekinthetőek lesznek a Bolyai Társulat honlapján (http://www.bolyai.hu/). Nagyon köszönjük a Bolyai Társulatnak és a komáromi szervezőknek, élükön Keszegh Istvánnal a gondos munkájukat. Viszontlátásra jövőre Pécsett!

 

A középiskolás tanárverseny feladatai

 

A verseny időtartama 90 perc volt. A feladatok pontozása: minden helyes válasz 5 pontot ért; helytelen válaszra 0 pont járt; válasz nélkül hagyott kérdésekre 1-1 pontot adtak.
1. Ha x, y és y-1x egyike sem nulla, akkor mennyi x-1yy-1x értéke? (A) 1; (B) xy; (C) yx; (D) xy-1xy; (E) Előző válaszok egyike sem helyes.
2. Mennyi a 5-24+3-8+7-48 kifejezés értéke? (A) 1; (B) 2-1; (C) 7-2; (D) 2; (E) 7-1.
3. Ha a+1a=3, akkor mennyi |a-1a| értéke? (A) 5; (B) 2; (C) 1,5; (D) 2; (E) 33.
4. 20112+20092010=? (A) 2009; (B) 2010; (C) 2011; (D) 2012; (E) 2013.
5. Ha 6x+7y=1213, 7x+6y=2011, akkor mennyi x+y értéke? (A) 248; (B) 249; (C) 250; (D) 251; (E) 252.
6. Mennyi x2-y2 értéke, ha x+y+x+y=72 és x-y-x-y=30? (A) 24; (B) 30; (C) 48; (D) 72; (E) Előző válaszok egyike sem helyes.
7. a1=7, an+1=|an2-16|, ahol n pozitív egész szám. a80=? (A) 1; (B) 7; (C) 15; (D) 17; (E) 33.
8. Ha x és y valós számok, akkor mennyi |1000-x|+|x-y|+|y-2011| legkisebb értéke? (A) 1000; (B) 1011; (C) 2011; (D) 3011; (E) 4022.
9. Hány megoldása van az |x-1|⋅|x+2|=|x+1|⋅|x-2| egyenletnek a valós számok körében? (A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
10. Hány gyöke van az xx+2=x5 egyenletnek a valós számok körében? (A) 2; (B) 3; (C) 4; (D) 5; (E) 6.
11. Mennyi az x2+y2+x-y+xy+2 kifejezés legkisebb értéke? (A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
12. Mennyi az x2-4x+1=0 egyenlet gyökei köbének összege? (A) 48; (B) 52; (C) 56; (D) 60; (E) 64.
13. log610⋅lg21610=? (A) 310; (B) 103; (C) -310; (D) -103; (E) Az előző válaszok egyike sem helyes.
14. Hány olyan n pozitív egész szám van, amelyre n3+2n2+9n+8 értéke köbszám? (A) 0; (B) 1; (C) 2; (D) 4; (E) végtelen sok.
15. Hány olyan pozitív egészekből álló (x;y) rendezett számpár van, amelyre
x2-y2=275? (A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
16. Mennyi az 1591 prímosztóinak összege? (A) 70; (B) 80; (C) 90; (D) 100; (E) 110.
17. Milyen számjegy áll abban a legkisebb 99-cel osztható pozitív egész számban második számjegyként, melynek minden számjegye páros? (A) 0; (B) 2; (C) 4; (D) 6; (E) 8.
18. Jelölje pi az i-edik prímszámot. Hány olyan pozitív egész n és k számpár van, amelyre ∏i=1npi=k2-1? (A) 0; (B) 1; (C) 2; (D) 3; (E) Végtelen sok.
19. Egy háromszög oldalainak hossza 13, 14 és 15 egység. Mekkora a háromszög területe? (A) 80; (B) 82; (C) 84; (D) 86; (E) 88.
20. Az O középpontú kör érintői a PA, PB és EC egyenesek. Ha PE=6, EA=2, akkor mekkora a PEC háromszög kerülete? (A) 15; (B) 16; (C) 17; (D) 18; (E) 19.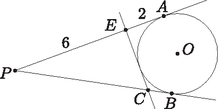
 
 

21. Egy számot nevezzünk páratlan kitevőjűnek, ha prímtényezős felbontásában minden kitevő páratlan. Ilyenek például 13=131, 54=2⋅33. Legtöbb hány egymást követő páratlan kitevőjű számot lehet megadni? (A) 4; (B) 5; (C) 6; (D) 7; (E) 8.
22. Legtöbb hány egymást követő számot lehet úgy megadni, hogy ne legyen közöttük a2⋅b alakú szám, ahol (a,b)=1 és a>1? (A) 4; (B) 5; (C) 6; (D) 7; (E) 8.
23. Egy számtani sorozatban az első tíz elem összege 100, az első száz elem összege 10. Mennyi az első száztíz elem összege? (A) -100; (B) 90; (C) 110; (D) -90; (E) -110.
24. Az ABCD húrtrapéz D-ből induló magasságának talppontja az AB alapon M. Tudjuk, hogy AM=4, MB=9 és ADB∢=90∘. Mekkora a trapéz területe? (A) 42; (B) 48; (C) 54; (D) 60; (E) 66.
25. Mi az logx(2x2+x-1)>logx2-1 egyenlőtlenség megoldáshalmaza a valós számok körében? (A) 12<x<1; (B) x>12 és x≠1; (C) x>1; (D) 0<x<1; (E) 12<x.
26. Az x, y valós számokra
y-x≤5y+4x≤-53y+2x≥-5}
teljesül. Mekkora x2+y2 legnagyobb értéke? (A) 13; (B) 14; (C) 15; (D) 16; (E) 17.
27. Melyik az a legkisebb n pozitív egész szám, amelyre nn nem osztója 2010!-nak? (A) 45; (B) 46; (C) 47; (D) 48; (E) 49.
28. Hány olyan rendezett {a,b,c,d} számnégyes van, melyre b<a, b<c, d<c, ahol a, b, c, d különböző pozitív egyjegyű számok? (A) 126; (B) 378; (C) 630; (D) 882; (E) 1134.
29. Az {1,2,3,4,...,100} halmaznak kiválasztottuk két részhalmazát, A-t és B-t úgy, hogy |A|=|B| és |A∩B|=0, továbbá ha n∈A, akkor 2n+2∈B. Mekkora |A∪B| maximuma? (A) 62; (B) 66; (C) 68; (D) 70; (E) 74.
30. Az 1,2,3,...,98,99 számokból kiválasztottunk 50 számot úgy, hogy semelyik kettő összege sem 99, sem 100. Mennyi a kiválasztott számok összege? (A) 2250; (B) 2275; (C) 2500; (D) 3550; (E) 3725.
 
A feladatsort Róka Sándor állította össze

 
A tanárverseny eredménye

Általános iskolában tanító tanárok:
1. Csordás Péter (Kecskemét, Katona József Gimn.) ..... 140 pont
2. Nagy Tibor (Kecskeméti Református Ált. Isk.) ..... 135 pont
3. Tóth Gabriella (Palics, Miroslav Antić Ált. Isk.) ..... 127 pont
4. Gunther Szilvia (Törökbálint) ..... 126 pont
5. Egyed László (Baja, III. Béla Gimn.) ..... 125 pont.
 

Középiskolában tanító tanárok:
1. Tassy Gergely (Budapest, Veres Péter Gimn.) ..... 136 pont
2. Horváth Eszter (Budapest, Szilágyi Erzsébet Gimn.) ..... 129 pont
3. Magyar Zsolt (Budapest, Szent István Gimn.) ..... 127 pont
4. Szigetiné Hornung Krisztina (Kaposvár, Zichy Mihály Iparművészeti Szakképző Isk.) ..... 126 pont
5. Erben Péter (Budapest, Berzsenyi D. Gimn.) ..... 124 pont
6. Besnyőné Titter Beáta (Budapest, Árpád Gimn.) ..... 123 pont
7. Fonyó Lajos (Keszthely, Vajda János Gimn.) ..... 119 pont.
1Berzsenyi György életéről és könyvtáráról Lapunk 2004. áprilisi számának 206‐207. oldalán olvasható cikk.