Cím:	A 2011‐2012. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2012/november, 455 - 461. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   A 2011‐2012. évi Arany Dániel Matematikai Tanulóverseny feladatai   KEZDŐK     I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók       Első (iskolai) forduló       1. Milyen arányban osztják az $ABCDEF$ szabályos hatszög $AC$ és $BF$ átlói egymást?     2. Az $N$ pozitív egész szám pozitív osztóinak a szorzata $3^{595}$. Határozzuk meg az $N$ szám utolsó számjegyét!     3. Mely $x$ és $y$ pozitív egész számokra igaz az alábbi egyenlőség? $\begin{array}{c}{\displaystyle x^2-y^2+2x-6y-25=0}\end{array}$       4. Egy zár, amelyen három nyomógomb van, akkor nyílik ki, ha a három különböző gombot egy meghatározott sorrendben közvetlenül egymás után nyomjuk meg. Legkevesebb hány gombnyomásra van szükség ahhoz, hogy biztosan kinyíljon a zár? (A megfelelő három gombnyomást esetlegesen megelőző gombnyomások sorozatának nincs hatása a zár szerkezetére.)     Második forduló       1. Mekkorák annak a deltoidnak a szögei, amelynek van körülírt köre, és az egyik átlója kétszer olyan hosszú, mint a másik?     2. Határozza meg azt a legkisebb $n$ pozitív egész számot, amelyre igaz, hogy $n$ egymást követő kétjegyű szám között mindig van olyan, amelyik osztható a számjegyeinek összegével.     3. Az $O$ középpontú, $AB=2r$ átmérőjű félkörön felvesszük egymás után a $C$ és a $D$ pontokat úgy, hogy az $AC$ és a $CD$ húrok hossza egyaránt $a$ és a $DB$ húr hossza $x$. Bizonyítsa be, hogy ha $a$ és $r$ mérőszáma racionális szám, akkor $x$ mérőszáma is racionális szám!     4. 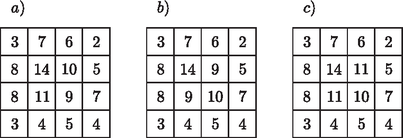Egy $4\times 4$-es táblázat minden mezőjében kezdetben a 0 szám áll. Egy-egy lépésben a tábla valamely $2\times 2$-es részletében a számok mindegyikét 1-gyel megnöveljük. Megkaphatjuk-e ilyen lépésekkel az alábbi kitöltéseket?       5. Tegyük fel, hogy $p$ és $d$ pozitív egész számok, amelyekre a $p$, $p+d$, $p+2d$, $\text{...}$, $p+10d$ számok mindegyike prímszám. Bizonyítsa be, hogy ekkor $d$ értéke legalább 210.     Harmadik (döntő) forduló       1. Az $ABCD$ téglalap $BC$ oldala 2 egység hosszúságú. Jelölje a $BC$ oldal felezőpontját $G$, a $CD$ oldal $C$ csúcshoz közelebbi harmadoló pontját $E$. Mekkora az $AB$ oldal, ha az $EAG$ szög ${30}^{\circ }$?     2. Egy háromszög oldalai a szokásos jelölésekkel $a$, $b$ és $c$, a velük szemközti szögek rendre $\alpha$, $\beta$ és $\gamma$. Mekkorák lehetnek a háromszög szögei, ha tudjuk, hogy a $\beta$ kétszerese az $\alpha$ szögnek és az oldalak között fennáll az $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=\frac{a}{c}+\frac{b}{a}+\frac{c}{b}$ összefüggés?     3. Pisti a következő játékot játssza. Először felír a táblára egy pozitív egész számot. Ezután minden lépésben letörli a táblán levő számot, s helyette, ha páros volt, akkor a szám felét, ha páratlan volt, akkor a nála 7-tel nagyobb számot írja fel. Jelöljük $A$-val, $B$-vel, illetve $C$-vel azon pozitív egész számok halmazát, melyekből kiindulva Pisti megkaphatja az 1, 3, illetve 7 számokat (a játékot utána is folytatja, miután ezek valamelyikét megkapta). $a)$ Bizonyítsuk be, hogy minden pozitív egész szám az $A$, $B$, $C$ halmazok közül pontosan az egyiknek eleme. $b)$ Hány 1 000 000-nál kisebb eleme van $A$-nak, $B$-nek, illetve $C$-nek?     II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók       Első (iskolai) forduló     Megegyezik az I. kategória első fordulós feladatsorával.     Második forduló     Megegyezik az I. kategória második fordulós feladatsorával.     Harmadik (döntő) forduló       1. Egy konferencián magyar, angol, francia, német, olasz és spanyol tudósok vettek részt. Valaki észrevette, hogy mindenkinek pontosan hat ismerőse van jelen, mind a hat nemzetből pontosan egy. (Az ismeretségek kölcsönösek, és senki nem számít a saját maga ismerősének.) $a)$ Bizonyítsuk be, hogy a résztvevők száma osztható 12-vel! $b)$ Bizonyítsuk be, hogy ha $n$ 12-vel osztható pozitív egész szám, akkor valóban létezhet ilyen konferencia pontosan $n$ résztvevővel!     2. Egy háromszög egyik csúcsából a másik két csúcshoz tartozó két belső és két külső szögfelezőre merőlegeseket állítunk. Ezek a szögfelezőket a $D$, $E$, $F$ és $G$ pontokban metszik. Bizonyítsuk be, hogy ez a négy pont egy egyenesre illeszkedik!     3. Tudjuk, hogy $a+\frac{1}{a}=p$, ahol $p$ prímszám. Bizonyítsuk be, hogy ekkor $\begin{array}{c}{\displaystyle A=a^4+a^3+a^2+\frac{1}{a^4}+\frac{1}{a^3}+\frac{1}{a^2}}\end{array}$ egész szám! Mennyi a $p$ értéke, ha $A$-nak négy pozitív osztója van?   III. kategória: Speciális tantervű osztályokban tanulók       Első (iskolai) forduló     Megegyezik az I. kategória második fordulós feladatsorával.   Második (döntő) forduló       1. Adott egy $k$ kör és rajta kívül egy $P$ pont. A $P$-ből a $k$-hoz húzott érintők érintési pontjai $Q$ és $R$. $Q$-ból húzzunk a $PR$-rel párhuzamost, és metssze ez a $k$ kört $A$-ban! Metssze továbbá az $AP$ szakasz a $k$ kört $B$-ben és $QB$ az $RP$-t $C$-ben! Igaz-e, hogy $RC=CP$?     2. Legyen $f$ a racionális számok halmazán értelmezett, valós értékű függvény. Tudjuk, hogy tetszőleges $x$, $y$ racionális számokra teljesül az $\begin{array}{c}{\displaystyle f\left(x+y\right)=f\left(x\right)+f\left(y\right)+xy}\end{array}$ egyenlőség. Adjuk meg az összes ilyen tulajdonságú $f$ függvényt!     3. Rögzített $k\ge 2$ egész szám esetén azt mondjuk, hogy az $n$ pozitív egész szám $k$-felbomló, ha létezik olyan $p$ prímszám és $a$ nem negatív egész szám, hogy: $\begin{array}{c}{\displaystyle n=p+a^k\mathrm{.}}\end{array}$ Bizonyítsuk be, hogy végtelen sok olyan $n$ pozitív egész szám létezik, mely egyetlen $2\le k\le 2012$ egész számra sem $k$-felbomló!   HALADÓK I. 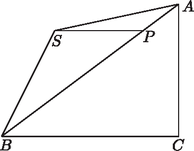kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók     Első (iskolai) forduló       1. Az ábrán látható $ABC$ derékszögű háromszög $AC$ oldala 6 cm, $BC$ oldala 8 cm hosszú. Az $SP$ szakasz párhuzamos $BC$-vel és fele olyan hosszú. Mekkora az $ABS$ háromszög területe? Bizonyítsuk be, hogy az $ABS$ háromszög területe nem függ a $P$ pont megválasztásától!         2. Az $ABCD$ négyzet $BC$ oldalával párhuzamos $e$ egyenes az $AB$ oldalt az $E$, a $CD$ oldalt pedig a $G$ pontban metszi. Az $AEGD$ és az $EBCG$ négyszög kerületének aránya $\lambda$. Ha $\frac{AE}{EB}=\mu$, akkor mekkora a $\left(2-\lambda \right)\cdot \left(2+\mu \right)$ szorzat értéke?     3. Az $f\left(x\right)=a{x}^2+bx+c$ másodfokú függvénynek $\left(x\in \text{R}\right)$ egy zérushelye van. Az $f\left(x\right)$ függvény mininumhelye $x=c$. Mekkora lehet az $ac$ szorzat értéke?     4. Bizonyítsuk be, hogy ${13}^n+3\cdot 5^{n-1}+8$ minden pozitív egész $n$ esetén osztható 24-gyel!     5. A Bergengóc királyi palota egyik folyosóját újra kell kövezni. A folyosó 20 dm széles és 99 dm hosszú. A felújítás idején kétféle járókövet lehet beszerezni: a kisebbik $4\text{dm}\times 4\text{dm}$-es és 100 garas az ára, a nagyobbik $5\text{dm}\times 5\text{dm}$-es és 130 garasba kerül. Mindkettő megvásárolható darabonként is. Legkevesebb hány garasból tudja a kincstárnok megoldani a folyosó kikövezését, ha a köveket nem szabad elvágni?     Második forduló       1. Bizonyítsuk be, hogy egy adott négyzet 2012 darab kisebb méretű négyzetre bontható úgy, hogy a kisebb méretű négyzetek oldalai párhuzamosak legyenek az eredeti négyzet oldalaival.     2. Hány olyan pozitív egész szám van, amelyre igaz, hogy számjegyeinek összege és szorzata is egyaránt 24?     3. Egy egyenlőszárú háromszög magasságpontja $M$, súlypontja $S$. Az $S$ pont rajta van a háromszög beírt körén. Mekkora az $MS$ szakasz és a háromszög alaphoz tartozó magasságának aránya?     4. Az $x^n+{\left(x+1\right)}^n+{\left(x+2\right)}^n+{\left(x+3\right)}^n+{\left(x+4\right)}^n+{\left(x+5\right)}^n+{\left(x+6\right)}^n$ összeg osztható 7-tel, ahol $x$ egész szám és $n$ pozitív egész szám. Oldjuk meg az $n<2012$ egyenlőtlenséget!     Harmadik (döntő) forduló       1. Bizonyítsa be, hogy ha az $ABCD$ paralelogramma hosszabbik átlója $AC$, $C$ merőleges vetülete $AB$-n $E$, $AD$-n $F$, akkor $\begin{array}{c}{\displaystyle AB\cdot AE+AD\cdot AF=A{C}^2\mathrm{.}}\end{array}$ Igaz-e az állítás az $AC<BD$ esetben?     2. Eszter naponta legalább egyszer bejelentkezik a Facebook-ra; de hogy ne vigye túlzásba, egy héten 12-nél többször sosem jelentkezik be. Mutassuk meg, hogy ki lehet választani néhány olyan egymás után következő napot, amelyek során összesen pontosan 20-szor jelentkezik be.     3. Két pozitív szám szorzata megegyezik az összegükkel. Mindkét szám olyan véges tizedestört, amely a tizedesvessző után két számjegyet tartalmaz úgy, hogy az utolsó számjegy 0-tól különböző. Melyik ez a két szám?     II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók       Első (iskolai) forduló       1. A minden valós számra értelmezett $f\left(x\right)=\frac{1}{2}{\left(x-2\right)}^2$ és $g\left(x\right)=mx$ függvény grafikonja érinti egymást, ahol $m$ valós paraméter. Hol lehet az érintési pont?     2. A Bergengóc királyi palota egyik folyosóját újra kell kövezni. A folyosó 20 dm széles és 99 dm hosszú. A felújítás idején kétféle járókövet lehet beszerezni: a kisebbik $4\text{dm}\times 4\text{dm}$-es és 100 garas az ára, a nagyobbik $5\text{dm}\times 5\text{dm}$-es és 130 garasba kerül. Mindkettő megvásárolható darabonként is. Legkevesebb hány garasból tudja a kincstárnok megoldani a folyosó kikövezését, ha a köveket nem szabad elvágni?     3. Egy trapéz átlói merőlegesek egymásra, az egyiknek a hossza 5 egység, a trapéz magassága 4 egység. Mekkora a területe?     4. Adottak az $n=\overline{abcabc}$ és $m=\overline{d00d}$ alakú hatjegyű, illetve négyjegyű természetes számok, ahol $a$, $b$, $c$ és $d$ nem feltétlenül különböző számjegyeket jelöl. $a)$ Mutassa ki, hogy $\sqrt[]{n}$ nem természetes szám! $b)$ Határozza meg azokat az $\left(n\mathrm{,}m\right)$ számpárokat, ahol $n=\overline{abcabc}$ és $m=\overline{d00d}$ alakú természetes számok, továbbá igaz, hogy $\sqrt[]{n+m}\in \text{N}$!     5. Bizonyítsuk be, hogy ha egy hatszög szemben fekvő oldalai párhuzamosak és a szemben fekvő csúcsokat összekötő három átló egyenlő egymással, akkor a hatszög csúcsai egy körön fekszenek, vagyis a hatszög köré kör rajzolható.     Második forduló       1. Mely $x$ és $y$ természetes számokra igaz, hogy $\sqrt[]{x}+\sqrt[]{y}=\sqrt[]{1000}$?     2. Legyen $A=1\underset{2k+1\text{ db}}{\overset{}{\underbrace{77\text{...}7}}}6$ és $B=3\underset{k\text{ db}}{\overset{}{\underbrace{55\text{...}5}}}2$  $2k+3$, illetve $k+2$ jegyű természetes szám. Bizonyítsuk be, hogy $\sqrt[]{A-B}$ is természetes szám, és határozzuk meg $\sqrt[]{A-B}$ jegyeinek számát!     3. Az $ABC$ háromszögben $AC=2AB$. Az $AB$ és $AC$ oldalon vegyük fel az $M$, illetve $N$ pontokat úgy, hogy az $\frac{AB}{2}=AM=CN=\frac{AC}{4}$ összefüggés teljesüljön. Jelölje $P$ az $MN$ és $Q$ a $BC$ szakaszok felezőpontját, $AD$ pedig a $BAC$ szög szögfelezőjét, ahol $D$ illeszkedik $BC$-re. Igazoljuk, hogy $PQ:AD=3:8$!     4. Egy 90 cm kerületű háromszög oldalai cm-ben mérve egész szám hosszúak. Mekkorák az oldalak, ha a háromszög egyik szöge egy másik szögének kétszerese?     Harmadik (döntő) forduló       1. Keressük meg az összes olyan kilencjegyű pozitív egész számot, melyben minden számjegy 1-től 9-ig csak egyszer szerepel, és az első, $i$ darab számjegyből képzett $i$ jegyű szám osztható $i$-vel $\left(i=\mathrm{1,}\text{...}\mathrm{,9}\right)$!     2. Az $ABC$ háromszögben $\alpha =2\beta =4\gamma$. A belső szögfelezők az $a$, $b$ és $c$ oldalt rendre a $D$, $E$ és $F$ pontokban metszik. Bizonyítsuk be, hogy $DE=DF$!     3. Hány olyan pozitív egész számokból álló $\left(x;y\right)$ számpár van, amely kielégíti az $a)$ $x^2-y^2={2012}^{2011}$, $b)$ $x^2+y^2={2012}^{2011}$ egyenletet?   III. kategória: Speciális tantervű osztályokban tanulók       Első (iskolai) forduló       1. Bizonyítsuk be, hogy ha $n$ természetes szám, akkor   $S=\frac{2\sqrt[]{n+1}}{\sqrt[]{n+1}-\sqrt[]{n}}$ egész része nem lehet négyzetszám!     2. Kiszámoltuk, hogy hány olyan $n$-jegyű ($n>1$) szám van, ahol bármely két szomszédos jegy összege osztható 3-mal. A kapott eredmény végződhet-e 2012-re?     3. Az $ABC$ egyenlőszárú háromszög $k$ köréírt körét belülről, a háromszög $AC$ és $BC$ szárait pedig rendre a $P$ és $Q$ pontokban érinti a $k_1$ kör. Bizonyítsuk be, hogy $PQ$ felezőpontja az $ABC$ háromszög beírt körének középpontja!     4. Az $x$, $y$, $z$, $u$ valós számokra teljesül, hogy    $\begin{array}{c}{\displaystyle 4x\sqrt[]{4-x^2}-3y\sqrt[]{3-y^2}+2z\sqrt[]{2-z^2}-u\sqrt[]{1-u^2}=15.}\end{array}$ Mekkora az $x{y}^2{z}^{2}u$ szorzat értéke?     5. Felveszünk 30 különböző pontot a síkon úgy, hogy ne legyen három egy egyenesen. Minden pontot minden ponttal összekötünk, és az éleket pirossal vagy kékkel színezzük. Minden pontból pontosan 12 kék színű él indul ki, a többi pedig piros. Vizsgáljuk az így kialakult háromszögeket! Ha egy háromszög minden oldala ugyanolyan színű, akkor a belsejét is kiszínezzük. Összesen hány háromszöget színezünk be?     Második (döntő) forduló       1. Igazoljuk az alábbi egyenlőtlenséget! $\begin{array}{c}{\displaystyle \sqrt[8048]{1!\cdot 2!\cdot \text{...}\cdot 4023!\cdot {\left(1!\cdot 2!\cdot \text{...}\cdot 2012!\right)}^4}<2012!}\end{array}$       2. Van 2012 darab (nem feltétlenül különböző) pozitív számunk: $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_{2012}$, melyek összege $2S$. A $k$ természetes számot felezőnek nevezzük, ha az $a_i$ számok közül kiválasztható $k$, amelyek összege éppen $S$. Legfeljebb hány különböző $k$ természetes szám lehet felező?     3. 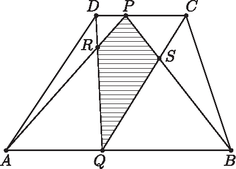Egy $ABCD$ trapéz $CD$ alapján adott egy $P$ belső pont (lásd ábra!). Hogyan válasszuk meg a másik $AB$ alap $Q$ belső pontját, ha azt szeretnénk, hogy a $PRQS$ négyszög területe a lehető legnagyobb legyen? ($R$ az $AP$ és a $DQ$ szakaszok metszéspontja, míg $S$ a $BP$ és a $CQ$ szakaszok metszéspontja).