Kezdőlap


Cím:	Pólya-féle urnamodell II.
Szerző(k):	Rudas Anna
Füzet:	2012/október, 398 - 402. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Pólya-féle urnamodell II.

4. Egyéb önmegerősítő folyamatok
4.1. Végtelen sok szín az urnában

Korábban ígértük, hogy szót ejtünk arról, hogyan tudnánk elérni, hogy ne csak egy előre rögzített, véges színhalmazból szerepelhessen golyó az urnában.
Tegyünk az urnába kezdetben pusztán egy darab golyót, aminek speciális szerepe lesz, nevezzük fekete golyónak, és módosítsuk a golyóhúzási algoritmust egy kissé a következőképpen. Ugyanúgy mint eddig, egy lépes kezdődjön azzal, hogy kihúzunk egy golyót véletlenszerűen az urnából. Hogyha

$a)$	a fekete golyót húzzuk, akkor a visszatételével egyidőben egy új golyót is teszünk az urnába, de nem feketét, hanem egy olyan színűt, amilyen ott addig még nem szerepelt,

$b)$	ha pedig nem a fekete golyót húzzuk, akkor úgy járjunk el, mint korábban, az eredeti Pólya-urna esetében, azaz a kihúzott színnel megegyezően tegyünk új golyót az urnába.

4.2. Kínai vendéglő folyamat

A fent vázolt modell, illetve ennek további általánosításai nagy jelentőséget kapnak olyan modellezési esetekben, amikor egy véletlen adathalmazt csoportokra kell osztani, de a csoportok száma előre nem ismert. A modellcsalád neve ,,kínai vendéglő folyamat''.
Hogy a név ne csak szórakoztatóan hangozzék, hanem érthetővé és megjegyezhetővé is váljon, a modellcsalád alapesetét az irodalomban elterjedt módot követve a következő példával illusztráljuk. Képzeljünk el egy kínai vendéglőt, amelyben végtelen sok, végtelen kapacitású kerek asztal található. Kezdetben minden asztal üres, majd egyesével kezdenek megérkezni a vendégek. Az érkező vendég eldönti, hogy megkezd egy új asztalt, vagy pedig véletlenszerűen választ a jelenlévő emberek közül valakit, és leül az ő bal oldalára (akik esetleg már az illető bal oldalán ültek, azok illedelmesen helyet szorítanak az érkezőnek). Az új asztal választásának valószínűségét a következőképp határozzuk meg. Ha érkezésekor

n

vendég tartózkodik már a vendéglőben, akkor az új vendég

$a)$	új asztalt kezd, ennek valószínűsége $1 / (n + 1)$ , vagy

$b)$	választ egyet a már ottlévő emberek közül véletlenszerűen, és mellé ül le, ez $\frac{n}{n + 1}$ valószínűséggel történik. Bármely már ott lévő ember választásának valószínűsége tehát $\frac{1}{n + 1}$ .

A leírás a legelső vendégre is érvényes, hiszen az ő esetében az új asztal választásának valószínűsége 1-nek adódik a képletből.
Egy-egy új asztal megkezdése megfeleltethető a Pólya-féle modell 4.1-beli változatában a fekete golyó húzásának, így minden asztal a kínai vendéglőben természetes módon egy-egy szín az urnában. Egy kiszemelt asztalnál ülő emberek száma ilyen módon megfelel az ehhez az asztalhoz tartozó színű golyók számának. Hogy miért van értelme mégis külön modellként tekinteni a kínai vendéglő folyamatra, az az általánosabb eset leírásakor lesz látható (lásd 4.4. szakasz).

4.3. Ropi-töredezési folyamat

Bizonyítás nélkül jegyezzük itt meg, hogy a kínai vendéglő folyamatnak is van értelme végtelen határesetéről beszélni. Ezzel egy másik beszélő nevű folyamathoz, az úgynevezett ropi-töredezési folyamathoz jutunk.
A ropi-töredezési folyamat a következőt jelenti. Veszünk egy egységnyi hosszúságú ropit, és véletlenszerűen kettétörjük, a törési pontnak a ropi bal szélétől való távolságát egyenletes eloszlás szerint választva. A bal kezünkben maradt ropidarabot félretesszük. Ezután a jobb kezünkben lévő ropidarabot tekintjük egységnyi hosszúságúnak, megint letörünk belőle egy egyenletes eloszlás szerint kisorsolt hosszúságú darabot, félretesszük, és így tovább. A végén az eredeti ropinak egy véletlen, végtelen feltöredezését kapjuk.
A kapcsolat a ropi-töredezés és a kínai vendéglő folyamat között az, hogy ha ,,végtelen hosszú idő múlva'' megnézzük, hogy a vendéglőben milyen arányban ülnek az emberek az elsőnek megkezdett asztalnál, az épp megfelel az egységnyi hosszúságú ropiból elsőnek letört darabka hosszának. A második asztal népszerűsége a másodikként letört ropidarab hossza, és így tovább.
Hihetővé válik ez az állítás, ha megfontoljuk a következőket. A 4.1. fejezetbeli modellben gondolatban az első szín kivételével az összes többire ,,váljunk színvakokká'', azaz a második, harmadik, stb. színeket mossuk össze egyetlen színné. Ezzel felfedeztük a két színű esetet a végtelen sok színű modellbe ágyazva. Korábban láttuk, hogy a két színt tartalmazó modellben az első szín arányának eloszlása az egyenleteshez tart ‐ ez tehát magyarázza a jelen modellben az első szín arányának egyenletes eloszlását a limeszben.
Most pedig tekintsük csak azokat a véletlen lépéseket, amikor nem az első, hanem valamelyik másik színből teszünk újat az urnába. Ezzel ,,letörtük'' a ropiból az első színnek megfelelő részt, és csak a többivel foglalkozunk. Az iménti gondolatmenetet folytatva tovább, most a második színt különböztetjük meg, a harmadik színtől kezdve a többit viszont tekintsük egyformának. Látjuk ilyen módon, hogy a második szín arányát a limeszben valóban a maradék ropidarab egyenletes véletlen kettétöréseként kaphatjuk (és így tovább).

4.1. feladat. Válasszunk az

{1,2, ..., n}

halmaz összes permutációi közül egyet egyenletesen véletlenül. Mi a valószínűsége, hogy az a ciklus, amelyikbe az

1

-es szám esik, épp

k

hosszú?

4.2. feladat. Válasszunk az összes

n

elemű permutáció közül egyet egyenletesen véletlenül. Mi a valószínűsége, hogy a benne szereplő leghosszabb ciklus

n / 2

-nél hosszabb?

4.4. Általánosabb eset

A kínai vendéglő folyamatnak léteznek általánosabb esetei. Egyik ilyen az, amikor rögzítünk egy tetszőleges pozitív valós számot,

α \in R^{+}

, mint a modell paraméterét. Az új vendég véletlen döntési szabálya ezzel a paraméterrel a következőképp módosul. Ha az érkezésekor a jelen lévő vendégek száma

n

, akkor az új vendég

$a)$	új asztalt bont, ennek valószínűsége $\frac{α}{n + α}$ , vagy

$b)$	egyenletesen választ egyet a már jelenlévő vendégek közül, és mellette foglal helyet, azaz bármely már jelenlévő vendég választásának esélye $\frac{1}{n + α}$ . Annak a valószínűsége tehát, hogy egy kiszemelt, éppen $k$ vendéggel rendelkező asztalt választ, $\frac{k}{n + α}$ .

α

paraméter nagysága határozza meg, hogy hosszú idő múlva kevés asztalhoz tömörült nagy létszámú csoportokat fogunk-e látni (kicsi

α

esete), vagy pedig sok-sok asztalnál elszórtan ülnek majd az emberek (nagy

α

esete). A Pólya-féle urnamodellnek a 4.1. fejezetben vázolt esete az

α = 1

paraméterválasztásnak felel meg, ami épp a ,,kicsi'' és a ,,nagy'' paramétertartományt választja el egymástól.
Általános

α

paraméter esetén a kínai vendéglőnek megfelelő pálcika töredezési folyamat annyiban módosul, hogy nem egyenletes, hanem (

α

-tól függő) paraméterű Béta eloszlással törjük le a darabkákat.

4.5. Véletlen fa

A 4.2. fejezetben vázolt kínai vendéglő folyamat kapcsán természetes módon felmerülhet bennünk az igény, hogy az asztalok adott pillanatbeli ,,népszerűségén'' túl azt is számon tartsuk, az egyes vendégek ,,miért'' az adott helyre ültek le. Más szóval, hogy ki volt az a vendég, akire a választásuk esett: mennyire ,,népszerűek'' az egyes egyének. Olyan ez, mintha azt kérdeznénk, melyik vendégnek hány ,,leszármazottja'' van, abban az értelemben, hogy hány ember ült le az illető vendég asztalához közvetve vagy közvetlenül miatta.
Tekintsünk egy olyan családfát, melyben csak az apa-fiú kapcsolatokat jelöljük (bármely emberhez tehát csak egy szülőt tartunk nyilván). Miközben véletlenül fejlesztjük a kínai vendéglő folyamatot, rajzoljunk fel lépésről lépésre egy fát, amiben a vendégek ilyen ,,kapcsolatait'' reprezentáljuk (ld. 6. ábra).

6. ábra. Véletlen fa az első kilenc lépés után

Kezdetben, amikor üres a vendéglő, rajzoljuk meg a fa gyökerét, azaz egyetlen csúcsot. Az első lépésben megérkezik az első vendég, ekkor rajzoljunk a fa első szintjére egy új csúcsot (címkézzük 1-gyel), és kössük össze a gyökérrel. A következő lépésben jön a második vendég, és választ magának véletlenül egy helyet. Jelöljük ezt egy új csúccsal (2-es címkével) a fában a következőképpen:

$a)$	ha a vendég új asztalt bont, akkor rajzoljuk az új csúcsot az első szintre, és kössük össze a gyökérrel,

$b)$	ha pedig az első vendég mellé ült le, akkor az új csúcsot a fa második szintjére rajzoljuk, és kössük össze az 1-es csúccsal.

A többi vendég helyválasztását hasonlóan számon tartjuk egy-egy új csúcs megjelenítésével a fában: a vendég érkezési sorszámával címkézett csúcsot az általa választott régi vendég ,,fiaként'' rajzoljuk a családfába. A címkék használata biztosítja, hogy az azonos ,,apához'' tartozó ,,fiúk'' között a korbeli sorrend rekonstruálható legyen.
Ezzel egy véletlenül növekedő fa folyamatot hoztunk létre, melyről egy-egy pillanatképet az 6. és a 7. ábrán láthatunk.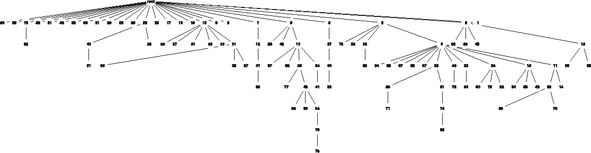

7. ábra. Véletlen fa kilencvenkilenc lépés után

Világos, hogy a fa gyökerétől 1 távolságra lévő csúcsok a kínai vendéglőben az új asztalt kezdő vendégeknek felelnek meg, és ha ,,egy kalapba vesszük'' az összes olyan csúcsot, amely egy-egy ilyen újító hajlamú vendéghez tartozó részfában található, akkor a kínai vendéglőben létrejövő asztaloknál ülő vendégek csoportjait látjuk a fában.
Gazdagabb struktúrát nyertünk azonban ezzel a reprezentációval: segítségével azonnal szembetűnővé válik például a modellben meghúzódó önhasonlóság. Ha azt a véletlen pillanatot tekintjük ugyanis, amikor a

k

-adik ,,asztalt'' megkezdi valaki, és onnantól kezdve csak azokra a véletlen időpontokra koncentrálunk, amikor valaki más ahhoz a

k

-adik asztalhoz csatlakozik, akkor láthajuk, hogy az itt kialakuló véletlen részfa pontosan ugyanolyan szabályszerűség szerint épül, mint a teljes fa, vagy mint akármelyik másik asztalnak megfelelő másik részfa.
Véletlen fák illetve gráfok növekedésének híressé vált vizsgálata található [1]-ben. Az ott tárgyalt növekedési szabálynál általánosabb szabályok esetén növekedő véletlen fákra vonatkozó eredményekért lásd [2]-t.

4.6. Önmegerősítés (,,reinforcement'')

A Pólya-urna és a többi, jelen cikkben vázolt modell mind az úgynevezett ,,reinforcement'', vagy önmegerősítés jelenségét mutatják. Ilyen matematikai modell magyarázza tehát például azt is, hogy miért lett olyan elsöprően sikeres a Facebook. Egyre több emberben van igény arra, hogy csatlakozzon valamelyik közösségi oldalhoz, és ahhoz csatlakoznak, ahová meghívja őket valaki. Így a sok potenciális közösségi oldal közül a véletlen választja ki, hogy melyik lesz a legnagyobb. A véletlenség azonban egy idő elteltével ,,befagy'', ahogy egyre több és több ember csatlakozik, az egyes új résztvevők hatása egyre kisebb és kisebb. Utólag már nagyon sikeresnek mondható a Facebook, de ha az elején egy kicsit más a piros és zöld golyók aránya, akkor lehet, hogy másként alakultak volna a dolgok.

5. Ábrák forrásai

A szimulációt Python nyelven írtam. Az ezzel generált adatokat a 2. és 3. ábrák esetében Gnuplot programmal, a 7. ábra esetében pedig a szintén ingyenesen elérhető, nagyméretű gráfok testreszabott kirajzolására alkalmas Cytoscape programmal rajzoltam meg.
Az 5. ábra Gnuplottal készült, a kód alapja a

http://en.wikipedia.org/wiki/File:Beta_distribution_pdf.svg

honlapon elérhető kódrészlet.
A 4. és a 6. ábrát a LaTeX tikz csomagjával készítettem.

Hivatkozások

[1]	Albert-László Barabási, Réka Albert, Emergence of scaling in random networks, American Association for the Advancement of Science. Science, Vol. 286 (1999).

[2]	Anna Rudas, Bálint Tóth, Benedek Valkó, Random trees and general branching processes, Random Structures and Algorithms 31 (2007), 186‐202.

\begin{matrix} Rudas Anna \end{matrix}