| Cím: | Pólya-féle urnamodell I. | |
| Szerző(k): | Rudas Anna | |
| Füzet: | 2012/szeptember, 327 - 337. oldal |  PDF | MathML PDF | MathML |
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A valószínűségszámítás egyik alapvető gondolatkísérlete Pólya György (1887‐1985) nevéhez fűződik, és épp ezt a jelenségkört modellezi. Egy időben véletlenül növekedő rendszerben a kezdeti időszakban megvalósuló véletlen lépések olykor sokkal meghatározóbbá válnak a távoli jövőbeli véletlen kimenetel szempontjából, mint a későbbi lépések. A Pólya-féle urna folyamat után, a cikk második felében egyéb kapcsolódó modelleket is vázolunk, melyek mind erre a szálra fűzhetők fel. Ezeket a kombinatorikus megközelítéssel jól megérthető modelleket részletesen tárgyalja [2] és [3]. Magyar nyelven is elérhető, klasszikus leírásért lásd [1]-et. A szóhasználatról megjegyezzük, hogy bár az ,,urna'' kifejezés mai füllel kissé bizarrul hangozhat, a matematikus társadalom mégis ezt a szót használja történelmi okokból1, amikor dobozokban elhelyezett színes golyók véletlen kihúzásairól beszél. A magyar nyelvű matematikai irodalom is megőrzi ezt a szóhasználatot, és ennek megfelelően mi is így teszünk. A megértéshez a kombinatorikus valószínűség valamint a határérték fogalmának ismerete szükséges. Az egyéb felmerülő fogalmakat a szemléletességet szem előtt tartva igyekszem bemutatni. 2.1. A modell Az első lépés abból áll, hogy véletlenszerűen (minden golyónak azonos esélyt adva, azaz egyenletes eloszlással) kihúzzuk az egyik golyót a dobozból és megnézzük a színét, majd visszatesszük. Ezen kívül teszünk a dobozba még egy új golyót is, mégpedig olyan színűt, mint amilyet az imént húztunk. A dobozban tehát most három golyó van: ha pirosat húztunk, akkor egy zöld és két piros, ha pedig zöldet húztunk, akkor egy piros és két zöld. A dobozban lévő piros golyók arányát jelöljük -gyel, ami tehát lehet (pirosat húztunk) vagy (zöldet húztunk). Jöhet a második lépés: a most bent lévő három golyó közül húzunk véletlenül, egyenletes eloszlással, megnézzük a színét, visszatesszük a dobozba egy új, ugyanolyan színű golyóval együtt. A most ott lévő piros golyók aránya, , tehát lehet , vagy , attól függően, hogy mennyi volt , és hogy milyen színű golyót húztunk most (lásd 1. ábra). 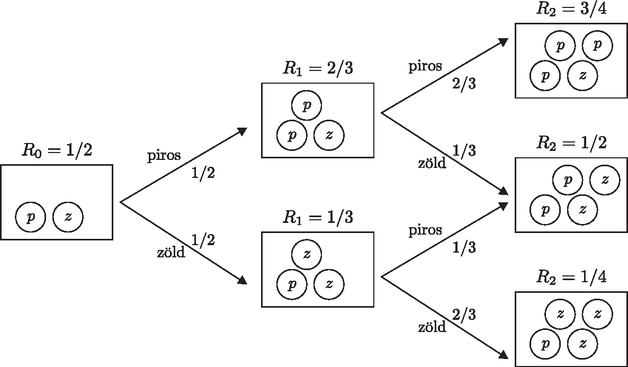 Ugyanígy haladva tovább, ezt az elemi lépést ismételjük meg egymás után sokszor. Hogyha a dobozban lépés után darab piros és darab zöld golyó található, azaz a piros golyók aránya
Ez a Pólya-féle urnamodell legegyszerűbb esete. Milyen szabályszerűséget fedezhetünk fel, rögzített mellett, az szám véletlen értékével kapcsolatban? Könnyen látható, hogy lehetséges értékei a intervallumban a alakú törtek, ahol , azaz ahogy egyre nagyobb, az értékkészlete kezdi egyenletesen sűrűn kitölteni a teljes intervallumot. De milyen eséllyel lesz értéke éppen , valamilyen adott -ra? Világos, hogy , a piros golyók aránya az -edik lépés után épp annak az aktuális (feltételes) valószínűségét adja meg, hogy a következő, -edik lépésnél piros színű golyót húzunk, feltéve, hogy már eljutottunk az -edik lépésig. Az első pár lépésben a megvalósulások valószínűségeit könnyen kiszámolhatjuk, például az 1. ábrát követve. értéke kétféle lehet,
értékének kiszámolásakor ezt már figyelembe vesszük. Az 1. ábráról leolvashatók a következő esetek valószínűségei:
Összességében tehát az értéket is eséllyel érjük el.
Azaz és esetében is teljesül az, hogy az összes lehetséges érték között egyenletesen oszlik el a valószínűség, más szóval a változó az értékkészletén egyenletes eloszlású. Véletlen-e, hogy és esetében ez így van?
Vegyünk egy rögzített értéket (), és indítsuk el ugyanannak a Pólya-urna kísérletnek sok () független példányát, mindig egy piros és egy zöld golyóval kezdve, és futtassuk lépésig. Ezekben a független kísérletekben mindig jegyezzük fel, mi jött ki értékére, és rajzoljuk fel a gyakorisági ábrát, más néven hisztogramot, ebből az kísérletből. Az általunk írt program segítségével előállított példa-hisztogramot lásd a 2. ábra tetején.  Tegyük fel, hogy az választást rögzítjük, de értékét, azaz a kísérletek számát változtatni akarjuk, és az eredményül kapott hisztogramokat össze akarjuk vetni egymással. Hogyha a különböző -ekre előállított hisztogramokat úgy normáljuk, hogy az oszlopok által lefedett tartomány területe mindig azonos legyen, akkor az összevetés kényelmes lesz, mert a lépték minden ábránkon azonos, lásd a 2. ábra alsó sorozatát. Rögzített mellett növelésével az ábra egyre inkább hasonlít a feladatban bizonyított elméleti eloszláshoz tartozó, egyenletes hisztogramhoz. Azt, hogy a hisztogramok növelésével valóban az elméletihez tartanak, a statisztika alaptétele mondja ki. A 2.2. feladat állításából kiolvasható, hogy növelésével elméleti eloszlása a intervallumon értelmezett úgynevezett folytonos egyenletes eloszláshoz tart (ennek úgynevezett ,,sűrűségfüggvénye'' a vízszintes vonal, ahol a vonal alatti terület 1-re van normálva). Ez már önmagában is érdekes tény, ámde ennél egy sokkal erősebb állítás is igaz. A következő fejezetben e felé az állítás felé haladunk. 3.1. A Pólya-féle urnamodell általánosabb esetei Általánosíthatjuk ennél jobban is az urna modellt. Például úgy, hogy nem csak két színt engedünk meg, hanem egy előre rögzített, elemszámú színhalmazból válogatva teszünk kezdetben az urnába darab színű, darab színű, , darab színű golyót. Ha az olvasóban felmerül, meg tudunk-e engedni végtelen sok színt is, még egy kis türelmet kérünk tőle, egy későbbi fejezetből ez is ki fog derülni. Egyelőre maradjunk a két szín használata melletti általánosításnál, mert ez is rejteget még érdekességet. A 2.2. feladatban bizonyított állítás rögzített mellett mond valamit az véletlen szám (valószínűségi változó) lehetséges értékeiről, és az értékek megvalósulásának valószínűségeiről (a valószínűségi változó eloszlásáról). Olyan típusú eredmény ez, mint mikor a 2.3. feladatban megírt programunk futásakor nem írattuk ki a futás közben érintett értékeket , hanem minden egyes futáskor csak az általunk előre kiszemelt mellett voltunk kíváncsiak kimeneteleire. Hogy éppen hogyan jutottunk el addig a véletlen számig, azt nem vizsgáltuk. Természetes módon felmerülhet bennünk ugyanakkor a kérdés, megállapíthatunk-e valamit a véletlen számsorozat egészéről (véletlen folyamatról) is, ami egy-egy ilyen szimuláció során előáll. Feljegyezhetnénk sok, egymástól függetlenül előálló ilyen sorozatot, és ezekről a véletlen sorozatokról is megkérdezhetnénk, vajon milyen tulajdonságokkal rendelkeznek. Az általunk írt programmal készített trajektóriákat lásd a 3. ábrán. Ezek megfigyelésével máris tehetünk néhány kezdeti megállapítást. 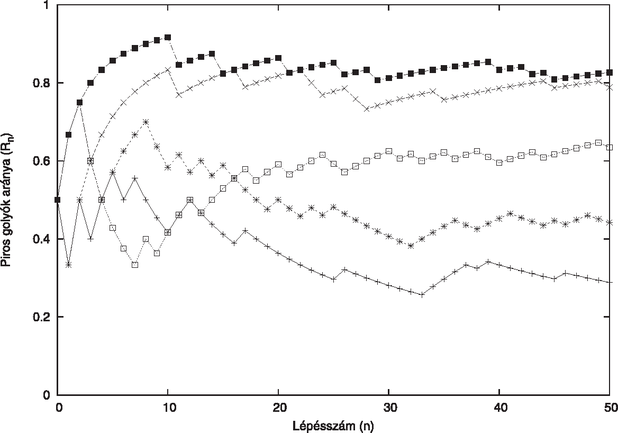 Az algoritmusról általánosságban megállapíthatjuk azt, hogy a piros golyó húzásának éppen aktuális valószínűsége időben véletlenszerűen változik, ahogyan az urnában a piros golyók aránya az összes golyóhoz képest mindig más és más. Ugyanakkor egyetlen golyó betételének hatása erre az arányra, ahogy haladunk előre az időben, egyre kisebb és kisebb, hiszen az új golyó megjelenése az éppen aktuális arányt már egyre kevésbé tudja megváltoztatni. Azok a véletlen folyamatok, amelyek mindig az éppen aktuális (véletlen) pozíciójukat ,,szeretnék megtartani'', különös jelentőségük van, és a martingál elnevezést kapták. Ezek, ha egy adott lépéskor megfigyeljük őket, a véletlen érték ismeretében a következő lépésben ,,várhatóan'' pontosan ugyanott maradnak. Ez nem azt jelenti, hogy a következő lépésben nem mozdulnak el, hanem azt, hogy a valószínűségekkel súlyozott átlagos elmozdulásuk nulla. A témakörben az egyik leggyakrabban használt tétel szerint pedig, ismét nem teljesen precízen megfogalmazva, hogyha egy ilyen véletlen folyamat értékkészlete korlátos, akkor annak a véletlen folyamatnak bármilyen tipikus megvalósulása olyan számsorozat lesz, amelynek létezik a határértéke. (A ,,tipikus megvalósulás'' fogalmát jelen cikkben nem definiáljuk.) Ahhoz, hogy lássuk, ez az erős tétel valóban alkalmazható a Pólya-féle urnamodell fenti általánosításainak esetében, a két feltétel fennállását vizsgáljuk. Az értékkészlet nyilvánvalóan korlátos, csak -ben mozog, tehát a tétel másik feltétele rögtön teljesül. A másik feltétel igazolása érdekében ellenőrizzük, hogy a martingálokat definiáló tulajdonság igaz az folyamatra. Képzeljük el, hogy lépést már megtettünk, és a szokásos módon jelöljük -nel az -edik lépés után a piros golyók számát, -nel a zöldek számát, -nel pedig a piros golyók arányát az összeshez képest. Ekkor
Hogy mennyi az szám ismeretében feltételes várható értéke, úgy kapjuk meg, hogy mindkét szóba jövő értéket megszorozzuk a valószínűségükkel, majd összeadjuk őket: Ennek a számolásnak az eredménye épp , azaz a folyamat -edik lépésében kapott érték ismeretében a következő lépés által okozott elmozdulás feltételes várható értéke nulla. Ez a számolás és bármely értéke mellett érvényes. A Pólya-féle urnamodellben a vizsgált véletlen folyamat tehát valóban egy korlátos martingál, aminek a 3.3. szakaszban vázolt tétel szerint tehát létezik a határértéke (ami azonban egy véletlen szám!). A határérték valószínűségi eloszlása a folytonos egyenletes eloszlás a intervallumon. Ez összefoglalva tehát azt jelenti, hogy a véletlen trajektóriák, melyeknek véges szeleteit a számítógépes programunkkal meg is figyelhetjük (3. ábra), ,,végtelen hosszú ideig futtatva'' mind beállnak egy-egy (véletlen) értékre. Kódoljuk az lépésből álló kísérleteket egy-egy -hosszú, és betűkből álló sorozattal, azaz a trajektóriákat kódoljuk a elemeivel, az egymás után kihúzott golyók színének megfelelően. E halmaz azon részhalmazát, mely sorozatokban pontosan darab betű szerepel, jelölje , ennek elemszáma A 2.1. feladat szakaszának megoldásakor kapott kombinatorikus formulából kiolvasható, hogy adott mellett egy rögzített arány, azaz rögzített számú piros golyó összes lehetséges előállási sorrendje mind azonos valószínűséggel történik. Ez azt jelenti, hogy az arányhoz vezető -hosszú trajektóriák, a halmaz elemei mind egyforma valószínűséggel állnak elő. Vegyünk egy hamis érmét, mégpedig olyat, ami rögzített valószínűséggel esik a piros oldalával felfelé, valószínűséggel pedig a zöld oldalával felfelé. Egy kísérlet álljon abból, hogy feldobjuk ezt az érmét -szer, a dobások egymástól legyenek függetlenek, és jegyezzük fel a dobások eredményeit és betűkkel. Ha -et egyre inkább növeljük, akkor a fenti, hamis érmés kísérlet eredményeképp előálló sorozatban egyre valószínűbb, hogy a betűk aránya közel van -hez. Ezt úgy hívják, hogy a nagy számok gyenge törvénye. A nagy számok erős törvénye is igaz, ami pedig azt mondja ki, hogy ha előállítunk egy ,,végtelen hosszú'' sorozatot egy hamis érmével, legyen a hamis érme piros oldallal felfelé esésének valószínűsége , akkor a véletlen sorozat egyre hosszabb véges szeleteit nézve a benne szereplő betűk aránya -hoz tart. Ha tehát rögzítünk egy értéket, akkor azon feltétel mellett, hogy a Pólya-féle urnamodell trajektóriája épp ehhez a -hoz tart, magát a trajektóriát előállíthatjuk úgy is, hogy veszünk egy -hamis érmét, és azt végtelen sokszor feldobjuk. A 3.3. szakaszban pedig láttuk, hogy a határérték, egyenletes eloszlású valószínűségi változó a intervallumon. Az eddigi megfigyeléseket összerakva tehát a következőt kaptuk. Vegyünk egy valószínűségi változót, amely egyenletes eloszlású a intervallumon. A kisorsolt érték legyen , ez tehát most már egy ismert érték a intervallumból. Vegyünk egy hamis érmét, amely ezzel a valószínűséggel esik a piros oldalával felfelé, valószínűséggel pedig a zöld oldalával felfelé. Dobjuk fel ezt az érmét végtelen sokszor, és jegyezzük fel a dobások eredményeit és betűkkel. Az így kapott végtelen sorozat ugyanolyan eloszlású, mint amit a Pólya-féle urnamodell alapesetében, a kihúzott golyók színét feljegyezve kapunk. A Pólya-féle urnamodell két színt használó eseteinek trajektóriáit kézenfekvő módon tekinthetjük egy negyedsík egész koordinátájú rácspontjain való bolyongásnak is. Az tengelyen jelöljük a piros, az tengelyen pedig a zöld golyók számát. A pályák a pontból indulnak, és az pontból kétfelé léphetnek: az pontba valószínűséggel, az pontba pedig valószínűséggel (lásd 4. ábra). 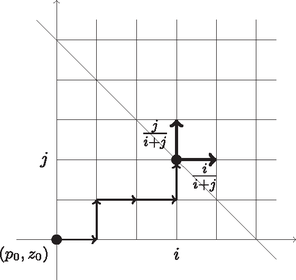 negyedsík rácspontjain Ebben a reprezentációban egyenletes eloszlása a és pontokat összekötő átlós egyenes által tartalmazott rácspontokon valósul meg. A véletlen határérték pedig felfogható egy véletlen iránynak a szögtartományban.  Érdekes megfigyelni, milyen hatása van annak, ha kezdetben ugyanannyi piros és zöld golyót teszünk a dobozba, de nem egyet-egyet, hanem például ötöt-ötöt, vagy húszat-húszat. A határérték-hisztogram egyre csúcsosabbá válik. Ez is azt sejteti, hogy konvergál a folyamat: minél nagyobb , annál kevésbé távolodik el a kezdeti értéktől, még akkor is, ha már nagyon nagy. Az elnevezés említése kedvéért álljon itt az is, hogy ha több, előre rögzített számú ( db) színnel indítunk, akkor az arányok vektora, amint -nel a végtelenbe tartunk, az úgynevezett Dirichlet-eloszláscsalád kezdeti állapottól függően paraméterezett tagjához tart.
1Már Jacob Bernoulli 1713-as Ars Conjectandi c. munkájában is a latin urna szó jelenik meg, ő ebben az agyag edényben helyez el gondolatban színes kavicsokat, ezek közül húz ki gondolatban egy pár darabot, és az így az urnában maradó véletlen kavicshalmazban vizsgálja a különböző színek arányának eloszlását.2A cikkben szereplő szimulációkat Python nyelven írtam, a kód szerkesztéséhez és futtatásához Eclipse-t használtam (Pydev modullal), a képek megjelenítéséhez pedig Gnuplot-ot. Ezek mindegyike ingyen hozzáférhető. |