Cím:	Megoldásvázlatok a 2012/4. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Koncz Levente
Füzet:	2012/május, 275 - 282. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2012/4. sz. emelt szintű gyakorló feladataihoz     I. rész     1. Egy számtani sorozat differenciája $56$, $n$-edik eleme $2012$. A sorozat első $n$ elemének összege $32000$. Határozzuk meg a sorozat első elemét.  (12 pont)     Megoldás. A számtani sorozat $n$-edik eleme: $2012=a_1+\left(n-1\right)\cdot 56$, ebből pedig $a_1=2068-56n$. A számtani sorozat első $n$ elemének összege: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 32000}& {\displaystyle =\frac{\left[2a_1+\left(n-1\right)\cdot 56\right]\cdot n}{2}=\frac{\left[2\cdot \left(2068-56n\right)+\left(n-1\right)\cdot 56\right]\cdot n}{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\left(4080-56n\right)\cdot n}{2}=\left(2040-28n\right)\cdot n\mathrm{,}}\hfill \end{array}}$ ezt pedig nullára rendezve és 4-gyel osztva: $\begin{array}{c}{\displaystyle 7n^2-510n+8000=0.}\end{array}$ A másodfokú egyenlet egyik gyöke nem egész, tehát nem megoldása a feladatnak, a másik gyöke: $n=50$. A sorozat első eleme tehát $\begin{array}{c}{\displaystyle a_1=2068-56n=2068-56\cdot 50=-732.}\end{array}$ Behelyettesítéssel ellenőrizhető, hogy ez valóban megoldása a feladatnak.   2. Egy közpark olyan egyenlő szárú háromszög alakú, melynek szárai $40$ méteresek, a szárak által bezárt szög pedig ${50}^{\circ }$-os. A szárak találkozásától egy $35$ méter sugarú körívet húznak. A köríven belüli részt füvesítik, a köríven kívüli részt pedig virágokkal ültetik be. $a)$ Határozzuk meg a beültetéshez szükséges virágtövek számát, ha egy négyzetméterre $30$ tő virágot számolnak. $b)$ A park kerületén körben és a körívnek a park belsejébe eső részére ösvényeket terveznek. Határozzuk meg az építendő ösvények teljes hosszúságát (a számítások során az ösvények szélességét elhanyagolhatjuk).  (13 pont)   Megoldás. $a)$ A körív teljes egészében a park belsejében húzódik, hiszen az egyenlő szárú háromszög alaphoz tartozó magassága $\begin{array}{c}{\displaystyle 40\cdot \text{cos}{25}^{\circ }\approx 36\mathrm{,}25\text{m}>35\text{m}\mathrm{.}}\end{array}$ A beültetendő terület az egyenlő szárú háromszög területének ($T_1$) és a körív által létrehozott körcikk területének ($T_2$) különbsége. 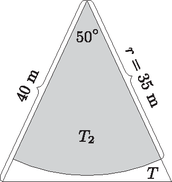${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_1}& {\displaystyle =\frac{40\cdot 40\cdot \text{sin}{50}^{\circ }}{2}\approx 612\mathrm{,}84{\text{m}}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle T_2}& {\displaystyle =\frac{{50}^{\circ }}{{360}^{\circ }}\cdot {35}^2\cdot \pi \approx 534\mathrm{,}51{\text{m}}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle T}& {\displaystyle =T_1-T_2\approx 78\mathrm{,}33{\text{m}}^2\mathrm{.}}\hfill \end{array}}$     A beültetéshez szükséges virágtövek száma a négyzetméterben mért alapterület 30-szorosa, tehát kb. 2350. $b)$ Az egyenlő szárú háromszög alapjának hossza $2\cdot 40\cdot \text{sin}{25}^{\circ }\approx 33\mathrm{,}81$ m. A körív hossza $\begin{array}{c}{\displaystyle \frac{{50}^{\circ }}{{360}^{\circ }}\cdot 2\cdot 35\cdot \pi \approx 30\mathrm{,}54\text{m}\mathrm{.}}\end{array}$ A megépítendő ösvények teljes hosszúsága tehát kb. $40+40+33\mathrm{,}81+30\mathrm{,}54\approx 144$ m.   3. Hány olyan nem izomorf, egyszerű gráf van, melynek pontjainak fokszámsorozata $a)$ 0, 1, 2, 3, 4, 5, 6, 7; $b)$ 2, 2, 3, 3, 3, 4, 5, 5; $c)$ 2, 3, 3, 4, 5, 5, 6; $d)$ 3, 3, 3, 5, 6, 6, 6; $e)$ 2; 3; 3; 4; 4; 4? Amelyik esetben nem létezik ilyen gráf, indokoljuk is meg, hogy miért nem.  (14 pont)   Megoldás. $a)$ Nincs ilyen gráf, mert bármely egyszerű gráfban kell lennie két azonos fokszámú pontnak. $b)$ Nincs ilyen gráf, mert bármely gráf pontjainak fokszámösszege páros. $c)$ A 6 fokszámú csúcsot jelölje $A$, az 5 fokszámúakat $B$ és $C$, a 4 fokszámút $D$, a 3 fokszámúakat $E$ és $F$, végül a 2 fokszámút $G$. Az $A$ csúcs biztosan össze van kötve az összes többivel. Ha $B$ és $C$ egymással nem lenne összekötve, akkor mindkettő össze lenne kötve $G$-vel, amelyből így már három él indulna ki, ez tehát nem lehetséges, a két 5 fokszámú csúcs össze van kötve egymással. Ha $B$ és $C$ valamelyike, például $B$ nincs összekötve $D$-vel, akkor viszont össze van kötve a maradék három csúccsal: $E$-vel, $F$-fel és $G$-vel. Ekkor $D$-ből indulnia kell élnek $C$-be, $E$-be és $F$-be is, viszont $C$-ből két él még hiányozna, tehát ez sem lehetséges, azaz $B$ és $C$ is össze van kötve $D$-ve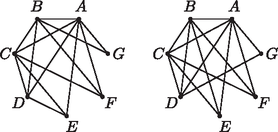l.     Ezután $B$-ből, $C$-ből és $D$-ből még összesen 5 élnek kell indulnia $E$-be, $F$-be és $G$-be, ami kétféleképpen valósítható meg aszerint, hogy a $D$-ből hiányzó egyetlen él másik végpontja egy 3 fokszámú vagy a 2 fokszámú csúcs. Tehát két, a feltételeknek megfelelő nem izomorf, egyszerű gráf van. $d)$ Nincs ilyen gráf. A három 6 fokszámú csúcs össze van kötve az összes többivel, de így a 3 fokszámúakból már nem is indulhat több él. Az 5 fokszámúból pedig két élnek még kellene indulnia, egyszerű gráfokban azonban nincs hurokél. $e)$ Ha a 4 fokszámú csúcsok közt mind a három lehetséges él be van húzva, akkor belőlük összesen még 6 élnek kell a másik három csúcs felé indulni, melyek fokszámösszege 8. Ez azt jelenti, hogy a másik három csúcs között összesen egy él van behúzva. Így két különböző gráfot kapunk aszerint, hogy ez az él a két 3 fokszámú csúcs közt húzódik vagy sem. 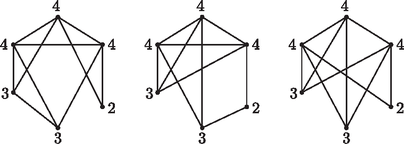    Ha a 4 fokszámú csúcsok közt két lehetséges él be van húzva, egy pedig nincs, akkor belőlük összesen még 8 élnek kell a másik három csúcs felé indulni, melyek fokszámösszege éppen 8, köztük tehát további élek ebben az esetben nincsenek. A gráf már egyértelműen meghatározott, hiszen az a két 4 fokszámú csúcs, melyek közt hiányzik az él, mindhárom további ponttal össze lesz kötve, a harmadik 4 fokszámú pedig csak a két 3 fokszámúval. Tehát összesen három, a feltételeknek megfelelő nem izomorf, egyszerű gráf van. 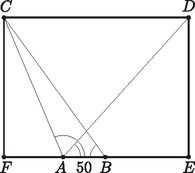  4. Téglalap alakú földdarabot szeretnénk felmérni. Ehhez a téglalap egyik oldalának belsejében felvesszük az egymástól $50$ méterre található $A$ és $B$ pontokat. A téglalapnak e két pontot tartalmazó oldalával szemközti csúcsait jelölje $C$ és $D$. Megmérjük a következő szögeket: $CAB$ szög ${113}^{\circ }$-os, $DAB$ szög ${48}^{\circ }$-os, $CBA$ szög ${54}^{\circ }$-os. Mekkora a földdarab területe?  (12 pont)   Megoldás. A téglalap $AB$ szakaszt tartalmazó oldalának két végpontját jelölje $E$ és $F$ az ábra szerint. Az $ABC$ háromszögben szinusztétellel meghatározható az $AC$ oldal hossza: $\begin{array}{c}{\displaystyle AC=AB\cdot \frac{\text{sin}{54}^{\circ }}{\text{sin}\left({180}^{\circ }-{54}^{\circ }-{113}^{\circ }\right)}=50\cdot \frac{\text{sin}{54}^{\circ }}{\text{sin}{13}^{\circ }}\approx 179\mathrm{,}8\text{m}\mathrm{.}}\end{array}$   Ezt felhasználva az $ACF$ háromszögben: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle CF}& {\displaystyle =AC\cdot \text{sin}{67}^{\circ }\approx 165\mathrm{,}5\text{m}\mathrm{,}}\hfill \\ \hfill {\displaystyle FA}& {\displaystyle =AC\cdot \text{cos}{67}^{\circ }\approx 70\mathrm{,}3\text{m}\mathrm{.}}\hfill \end{array}}$ Az $AED$ háromszögben: $\begin{array}{c}{\displaystyle AE=\frac{DE}{\text{tg}{48}^{\circ }}=\frac{CF}{\text{tg}{48}^{\circ }}\approx 149\mathrm{,}0\text{m}\mathrm{.}}\end{array}$     Így a földdarab területe: $\begin{array}{c}{\displaystyle T=CF\cdot FE=CF\cdot \left(FA+AE\right)=165\mathrm{,}5\cdot 219\mathrm{,}3\approx 36294{\text{m}}^2\mathrm{.}}\end{array}$   II. rész     5. Dani teniszezik. Egy versenyen első adogatásainak $63\%$-át ütötte érvényes területre. Ha érvényes területre ment az első adogatás, akkor a labdamenetek $90\%$-át megnyerte. Ha nem ment érvényes területre, akkor egy másodikat adogathatott. Ezeknek $85\%$-át ütötte érvényes területre. Amikor a második adogatás érvényes területre ment, akkor a labdamenetek $60\%$-át nyerte meg. Ha egyik adogatását sem ütötte érvényes területre, akkor Dani elveszítette a labdamenetet. $a)$ Mekkora a valószínűsége, hogy Dani elveszített egy labdamenetet, amikor ő adogathatott? $b)$ Mekkora a valószínűsége, hogy Dani első adogatása már érvényes területre ment, ha tudjuk, hogy az adott labdamenetet elveszítette?  (16 pont)   Megoldás. $a)$ Jelölje $A$ azt az eseményt, hogy Dani megnyer egy labdamenetet, $B_1$ azt az eseményt, hogy az első adogatása sikeres, $B_2$ azt az eseményt, hogy a második adogatása sikeres. Annak a valószínűsége, hogy Dani az első adogatásából nyerte meg a pontot: $\begin{array}{c}{\displaystyle P\left(A\mid B_1\right)\cdot P\left(B_1\right)=0\mathrm{,}9\cdot 0\mathrm{,}63=0\mathrm{,}567.}\end{array}$ Második adogatásra csak a labdamenetek 37%-ában kerül sor, amikor az első adogatása sikertelen volt. Annak a valószínűsége, hogy második adogatásából nyerte meg a pontot: $\begin{array}{c}{\displaystyle P\left(A\mid B_2\right)\cdot P\left(B_2\right)\cdot P\left(\overline{B_1}\right)=0\mathrm{,}6\cdot 0\mathrm{,}85\cdot 0\mathrm{,}37=0\mathrm{,}1887.}\end{array}$ Annak a valószínűsége, hogy Dani nyerte a pontot, az előző két érték összege, tehát $P\left(A\right)=0\mathrm{,}7557$, annak a valószínűsége pedig, hogy Dani elvesztette a labdamenetet, $\begin{array}{c}{\displaystyle P\left(\overline{A}\right)=1-P\left(A\right)=0\mathrm{,}2443.}\end{array}$ $b)$ A kérdés a $P\left(B_1\mid \overline{A}\right)$ valószínűség. A feltételes valószínűség definíciója szerint: $\begin{array}{c}{\displaystyle P\left(B_1\mid \overline{A}\right)=\frac{P\left(B_1\overline{A}\right)}{P\left(\overline{A}\right)}=\frac{P\left(\overline{A}\mid B_1\right)\cdot P\left(B_1\right)}{P\left(\overline{A}\right)}=\frac{0\mathrm{,}1\cdot 0\mathrm{,}63}{0\mathrm{,}2443}\approx 0\mathrm{,}258.}\end{array}$   6. $a)$ Határozzuk meg $\frac{x}{y}$ értékét három tizedesjegy pontossággal, ha tudjuk, hogy $2^x=5^y$, ahol $x$ és $y$ nullától különböző valós számok. $b)$ Oldjuk meg az alábbi egyenlőtlenséget a valós számok lehető legbővebb részhalmazán: $\begin{array}{c}{\displaystyle \frac{5}{2}\sqrt[]{\text{lg}x}+2\text{lg}\sqrt[]{\frac{1}{x}}-1<0.}\end{array}$ (16 pont)   Megoldás. $a)$ Vegyük mindkét oldal 10-es alapú logaritmusát és alkalmazzuk a logaritmus ismert azonosságait: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{lg}{2}^x}& {\displaystyle =\text{lg}{5}^y\mathrm{,}}\hfill \\ \hfill {\displaystyle x\text{lg}2}& {\displaystyle =y\text{lg}5.}\hfill \end{array}}$ Keresztbe osztva kapjuk: $\begin{array}{c}{\displaystyle \frac{x}{y}=\frac{\text{lg}5}{\text{lg}2}\approx 2\mathrm{,}322.}\end{array}$ $b)$ Először megállapítjuk az egyenlőtlenség értelmezési tartományát. A logaritmus függvény értelmezési tartománya miatt $x>0$, valamint $\sqrt[]{\frac{1}{x}}>0$, amiből szintén $x>0$ következik. A négyzetgyökfüggvény értelmezési tartománya miatt $\text{lg}x\ge 0$, amiből $x\ge 1$, valamint $\frac{1}{x}>0$, amiből ismét $x>0$ következik. Összegezve mindezt az egyenlőtlenség értelmezési tartománya $x\ge 1$. A bal oldalon álló kifejezés középső tagját a hatványozás és a logaritmus azonosságainak felhasználásával átalakítjuk: $\begin{array}{c}{\displaystyle 2\text{lg}\sqrt[]{\frac{1}{x}}=2\text{lg}{x}^{-\frac{1}{2}}=\left(-\frac{1}{2}\right)\cdot 2\text{lg}x=-\text{lg}x\mathrm{.}}\end{array}$ Az $a=\sqrt[]{\text{lg}x}$ (nemnegatív) új ismeretlen bevezetésével az egyenlőtlenség ezután így alakul: $-a^2+2\mathrm{,}5a-1<0$. A megfelelő egyenlet megoldásai $a=2$ és $a=0\mathrm{,}5$, a negatív főegyütthatóra tekintettel az egyenlőtlenség megoldása ezért $a<0\mathrm{,}5$, vagy $a>2$. Figyelembe véve, hogy $a$ nemnegatív, megoldandóak a $0\le \sqrt[]{\text{lg}x}<0\mathrm{,}5$ és a $\sqrt[]{\text{lg}x}>2$ egyenlőtlenségek. Ezeket négyzetre emelve adódik $0\le \text{lg}x<0\mathrm{,}25$, illetve $\text{lg}x>4$. Ezekből kapjuk, hogy $\begin{array}{c}{\displaystyle 1\le x<\sqrt[4]{10}\left(\approx 1\mathrm{,}778\right)\mathrm{,}\text{illetve}x>10000.}\end{array}$ Átalakításaink ekvivalensek voltak.   7. Az $f\left(x\right)=2\text{sin}x$ függvény grafikonja és az $x$ tengely által a $\left[0;\pi \right]$ intervallumon közrezárt síkidomot a $g\left(x\right)=2\text{cos}x$ függvény görbéje két síkidomra bontja. Határozzuk meg a két síkidom területének arányát.  (16 pont)   Megoldás. A teljes síkidom területét az $f$  0 és $\pi$ közötti integráljaként határozhatjuk meg: $\begin{array}{c}{\displaystyle T=\underset{0}{\overset{\pi }{\int }}2\text{sin}xdx={\left[-2\text{cos}x\right]}_0^{\pi }=-\left(-2\right)-\left(-2\right)=4.}\end{array}$ A $g$ függvény zérushelye ott van az adott intervallumban, ahol $\text{cos}x=0$, tehát $x=\frac{\pi }{2}$-nél. A két függvény grafikonjának metszéspontját a $2\text{sin}x=2\text{cos}x$ egyenlet megoldása adja. Ezt $\text{cos}x\ne 0$-val osztva kapjuk, hogy $\text{tg}x=1$, azaz a vizsgált intervallumban 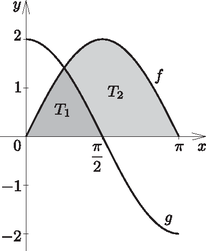$x=\frac{\pi }{4}$. Így ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_1}& {\displaystyle =\underset{0}{\overset{\frac{\pi }{4}}{\int }}2\text{sin}xdx+\underset{\frac{\pi }{4}}{\overset{\frac{\pi }{2}}{\int }}2\text{cos}xdx=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left[-2\text{cos}x\right]}_0^{\frac{\pi }{4}}+{\left[2\text{sin}x\right]}_{\frac{\pi }{4}}^{\frac{\pi }{2}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(-\sqrt[]{2}-\left(-2\right)\right)+\left(2-\sqrt[]{2}\right)=4-2\sqrt[]{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle T_2}& {\displaystyle =T-T_1=2\sqrt[]{2}\mathrm{.}}\hfill \end{array}}$     A két síkidom területének aránya: $\begin{array}{c}{\displaystyle \frac{T_1}{T_2}=\frac{4-2\sqrt[]{2}}{2\sqrt[]{2}}=\frac{4\sqrt[]{2}-4}{4}=\left(\sqrt[]{2}-1\right):1\approx 0\mathrm{,}414:1.}\end{array}$   8. Egy húrnégyszög átlói merőlegesek egymásra. Az átlók metszéspontja $E\left(2;1\right)$, a húrnégyszög $AB$ és $BC$ oldalának egyenlete $x+3y=10$, illetve $x-y+2=0$. Határozzuk meg a húrnégyszög csúcsainak koordinátáit és a négyszög köré írható kör egyenletét. $\begin{array}{c}\end{array}$ (16 pont)   Megoldás. A két megadott oldalegyenes egyenletéből álló egyenletrendszert megoldva kapjuk a $B$ pont koordinátáit. $BC$ egyenletéből $y=x+2$, ezt $AB$ egyenletébe visszaírva $x+3\left(x+2\right)=4x+6=10$, ahonnan $x=1$, majd $y=3$, tehát $B\left(1;3\right)$. A $BD$ átló egyenesének irányvektora például $\overrightarrow{EB}$, tehát a $\left(-1;2\right)$ vektor. Ezzel és az $E$ ponttal a $BD$ átló egyenletét felírhatjuk: $2x+y=5$. Az $AC$ átló merőleges erre az átlóra, ennek tehát normálvektora lesz a $\left(-1;2\right)$ vektor. Ezzel és az $E$ ponttal az $AC$ átló egyenlete: 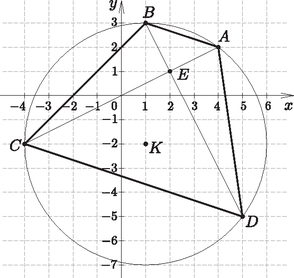$-x+2y=0$.     Az $A$ pont koordinátáit az $AC$ átló és az $AB$ oldalegyenes egyenletéből álló egyenletrendszer megoldásából kapjuk. Az átló egyenletéből $x=2y$, ezt $AB$ egyenletébe visszaírva $5y=10$, ahonnan $y=2$, majd $x=4$, tehát $A\left(4;2\right)$. A $C$ pont koordinátáit az $AC$ átló és a $BC$ oldalegyenes egyenletéből álló egyenletrendszer megoldásából kapjuk. Az átló egyenletéből $x=2y$, ezt $BC$ egyenletébe visszaírva $2y-y+2=0$, ahonnan $y=-2$, majd $x=-4$, tehát $C\left(-4;-2\right)$. A húrnégyszög köré írható kör megegyezik az $ABC$ háromszög köré írható körrel. Ennek $K$ középpontja megkapható például az $AC$ és a $BC$ oldal felezőmerőlegeseinek metszéspontjaként. Az $AC$ szakasz felezőpontja az origó, felezőmerőlegesének irányvektora megegyezik $AC$ egyik normálvektorával, ami például a $\left(-1;2\right)$ vektor. Ezekkel a felezőmerőleges egyenlete $2x+y=0$. A $BC$ szakasz felezőpontja $\left(-1\mathrm{,}5;0\mathrm{,}5\right)$, felezőmerőlegesének normálvektora például a $\overrightarrow{CB}$, tehát az $\left(5;5\right)$ vektor. Ezekkel a felezőmerőleges egyenlete $5x+5y=-5$, azaz $x+y+1=0$. A két felezőmerőleges egyenletéből álló egyenletrendszert kell megoldanunk. $AC$ felezőmerőlegesének egyenletéből $y=-2x$, ezt a másik egyenletbe beírva $x-2x+1=0$, ahonnan $x=1$, majd $y=-2$, tehát $K\left(1;-2\right)$. A kör sugarát megadja például a $KB$ távolság, ami 5 egység, a kör egyenlete így ${\left(x-1\right)}^2+{\left(y+2\right)}^2=25$. A $D$ pont koordinátáit végül a kör egyenletéből és a $BD$ átló egyenletéből álló egyenletrendszer megoldásaként kapjuk. A $BD$ egyenletéből $y=5-2x$, ezt visszaírva a kör egyenletébe ${\left(x-1\right)}^2+{\left(7-2x\right)}^2=25$. A zárójeleket felbontva és rendezve az $5x^2-30x+25=0$ egyenletet kapjuk, melynek megoldásai $x=1$ és $x=5$. Az előbbi a $B$ pontot adja meg, a másodikhoz tartozó $y$ érték $-5$, tehát $D\left(5;-5\right)$.   9. Egy duatlon verseny rajtja egy egyenes tengerparton van, célja a vízben. Egyik lehetőség a táv teljesítésére, hogy először 4 km-t futunk a parton, majd $90$ fokkal elfordulva 1 km-t úszunk a tengerben. Azonban megengedett bármikor letérni a futópályáról és elkezdeni úszni a cél felé. A homokos tengerparton 6 km/h, a vízben 2 km/h a sebességünk. A rajtvonaltól mérve milyen távolságra érdemes bevágni a vízbe, $a)$ ha futva és úszva egyenlő távolságot szeretnénk megtenni; $b)$ ha a lehető leghamarabb szeretnénk célba érni? Hány km-t kell ekkor úsznunk, és mennyi idő alatt tudjuk így teljesíteni a verseny távját? A válaszokat méter pontossággal adjuk meg.  (16 pont) 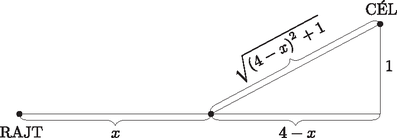  Megoldás. Jelölje $x$ azt a távolságot a rajtvonaltól mérve, amikor bevágunk a vízbe. Ekkor futva teszünk meg $x$ km-t, a vízben pedig az ábrán látható derékszögű háromszög átfogóját, azaz $\sqrt[]{{\left(4-x\right)}^2+1}$ km-t.     $a)$ Megoldandó az $x=\sqrt[]{{\left(4-x\right)}^2+1}$ egyenlet. Mindkét oldal pozitív, ezért   négyzetre emelhetünk: $x^2={\left(4-x\right)}^2+1$. Ebből kapjuk, hogy $x=\frac{17}{8}$. Tehát a rajtvonaltól mérve 2,125 km-re kell bevágnunk a vízbe. Ekkor az úszva megtett távolság is valóban ennyi, hiszen $\begin{array}{c}{\displaystyle \sqrt[]{{\left(4-\frac{17}{8}\right)}^2+1}=\sqrt[]{{\left(\frac{15}{8}\right)}^2+{\left(\frac{8}{8}\right)}^2}=\frac{17}{8}\mathrm{.}}\end{array}$ $b)$ A teljes táv megtételéhez szükséges időt ekkor a $\begin{array}{c}{\displaystyle t\left(x\right)=\frac{x}{6}+\frac{\sqrt[]{17-8x+x^2}}{2}\left(0<x<4\right)}\end{array}$ függvény adja meg. Ennek a függvénynek keressük a minimumát, amit ott vehet fel, ahol a deriváltja nulla. Az összetett függvények deriválási szabályát felhasználva: $\begin{array}{c}{\displaystyle t\text{'}\left(x\right)=\frac{1}{6}+\frac{2x-8}{4\sqrt[]{17-8x+x^2}}=0.}\end{array}$ Egyszerűsítve és rendezve: $12-3x=\sqrt[]{17-8x+x^2}$. Az $x$-re tett kikötés miatt a bal oldal is biztosan pozitív, így négyzetre emelhetünk, majd nullára rendezve a következő egyenletet kapjuk: $\begin{array}{c}{\displaystyle 8x^2-64x+127=0.}\end{array}$ Ennek megoldásai $x_{\mathrm{1,2}}=4\pm \frac{\sqrt[]{2}}{4}$, melyek közül csak a 4-nél   kisebb jön számításba, tehát $x=4-\frac{\sqrt[]{2}}{4}\approx 3\mathrm{,}646$. A $t\left(x\right)$ függvény folytonos, és ellenőrizhető, hogy első deriváltjának előjele $x$-ben negatívból pozitívba vált, így a kapott $x$ érték valóban minimumhelye $t$-nek. Tehát a rajtvonaltól számítva 3,646 km megtétele után érdemes elkezdenünk úszni. Az úszás távja ekkor $\begin{array}{c}{\displaystyle \sqrt[]{{\left(4-x\right)}^2+1}=\sqrt[]{{\left(\frac{\sqrt[]{2}}{4}\right)}^2+1}=\sqrt[]{\frac{18}{16}}=\frac{3\sqrt[]{2}}{4}\approx 1\mathrm{,}061\text{km}\mathrm{,}}\end{array}$ a teljes táv megtételéhez szükséges idő pedig $\begin{array}{c}{\displaystyle t\left(4-\frac{\sqrt[]{2}}{4}\right)=\frac{4}{6}-\frac{\sqrt[]{2}}{24}+\frac{3\sqrt[]{2}}{8}=\frac{4+2\sqrt[]{2}}{6}\approx 1\mathrm{,}138\text{ óra}\approx 68\mathrm{,}3\text{ perc.}}\end{array}$ (Ha végigfutnánk a 4 km-t, akkor 70 perc alatt teljesítenénk a versenyt.)   Megjegyzés: A Snellius‐Descartes-törvény felhasználásával a teljes visszaverődés határszöge is megoldást ad a feladatra.   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Koncz Levente</span><br>Budapest}}\hfill \end{array}}$