Cím:	Megoldásvázlatok a 2012/1. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Gyanó Éva
Füzet:	2012/február, 73 - 78. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2012/1. sz. emelt szintű gyakorló feladataihoz   I. rész     1. Oldjuk meg az alábbi egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle x^2+\frac{2x}{x+5}+\frac{1}{x^2+10x+25}=25.}\end{array}$ (12 pont)   Megoldás. A nevezők miatt: $x\ne -5$. Az egyenletet a következő alakba is írhatjuk: $\begin{array}{c}{\displaystyle {\left(x+\frac{1}{x+5}\right)}^2=25.}\end{array}$ Két eset lehetséges: I. eset: Ha $x+\frac{1}{x+5}=5$, akkor rendezés után az $x^2=24$ másodfokú egyenletet kapjuk. Ennek gyökei: $x_1=\sqrt[]{24}$, $x_2=-\sqrt[]{24}$. Mindkét gyök megoldása az egyenletnek. II. eset: $x+\frac{1}{x+5}=-5$, akkor rendezés után az $x^2+10x+26=0$ másodfokú egyenlethez jutunk. A diszkriminánsa negatív, így ebben az esetben nincs valós gyök. Az eredeti egyenlet két gyöke: $x_1=\sqrt[]{24}$, $x_2=-\sqrt[]{24}$.     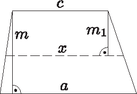2. Egy trapéz párhuzamos oldalai $a$ és $c$. Mekkora az a szakasz, amely párhuzamos az alapokkal, és felezi a trapéz területét?  (12 pont)   Megoldás. Jelölje a trapéz területét $T$, a felső kis trapézét $t_1$, az alsó kis trapézét pedig $t_2$. Tudjuk, hogy $T=2t_1$, illetve $T=2t_2$, azaz ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{a+c}{2}\cdot m=2\cdot \frac{x+c}{2}\cdot m_1\mathrm{,}}& \text{(<mn>1</mn>)}\\ \hfill {\displaystyle \frac{a+c}{2}\cdot m=2\cdot \frac{x+a}{2}\left(m-m_1\right)\mathrm{.}}& \text{(<mn>2</mn>)}\end{array}}$     Az (1) egyenletből $m_1=\frac{a+c}{2\left(x+c\right)}\cdot m$, ezt behelyettesítve a (2) egyenletbe: $\begin{array}{c}{\displaystyle \frac{a+c}{2}\cdot m=\left(x+a\right)\cdot \left(m-\frac{a+c}{2\cdot \left(x+c\right)}\cdot m\right)\mathrm{.}}\end{array}$ Az egyenletet $m$-mel ($m\ne 0$) osztva, majd néhány átalakítást végezve: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{a+c}{2}=\left(x+a\right)\cdot \left(1-\frac{a+c}{2\cdot \left(x+c\right)}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle a+c=\left(x+a\right)\cdot \left(2-\frac{a+c}{\left(x+c\right)}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(a+c\right)\left(x+c\right)=2\left(x+a\right)\left(x+c\right)-\left(x+a\right)\left(a+c\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle ax+ac+cx+c^2=2x^2+2cx+2ax+2ac-ax-cx-a^2-ac\mathrm{,}}\hfill \\ \hfill {\displaystyle c^2=2x^2-a^2\mathrm{.}}\hfill \end{array}}$ Vagyis a keresett szakasz hossza: $x=\sqrt[]{\frac{a^2+c^2}{2}}$.     3. Oldjuk meg az $\text{log}{}_x\left(5x^2\right)\cdot \text{log}{}_5^{2}x=1$ egyenletet a valós számok halmazán.  (13 pont)   Megoldás. Az egyenlet értelmezési tartománya: $x>0$ és $x\ne 1$. A logaritmus azonosságait felhasználva az egyenlet átírható a következő alakba: $\begin{array}{c}{\displaystyle \left(\text{log}{}_{x}5+\text{log}{}_x{x}^2\right)\cdot \text{log}{}_5^{2}x=\mathrm{1,}\left(\frac{1}{\text{log}{}_{5}x}+2\right)\cdot \text{log}{}_5^{2}x=1.}\end{array}$ A szorzást elvégezve és rendezve: $2\text{log}{}_5^{2}x+\text{log}{}_{5}x-1=0$. Ebből: $\begin{array}{c}{\displaystyle {\left(\text{log}{}_{5}x\right)}_1=\frac{1}{2}\mathrm{,}{\left(\text{log}{}_{5}x\right)}_2=-1.}\end{array}$ Az egyenlet megoldása: $x_1=\sqrt[]{5}$, $x_2=\frac{1}{5}$.     4. Egy büfében szendvicset és pizzát árulnak. Egy szendvicsen $30\%$, egy pizzán $50\%$ haszna van a kereskedőnek. Egyik nap ugyanannyi szendvicset adott el, mint pizzát, így $34\%$ haszna lett. Másnap viszont kétszer annyi pizzát vettek meg, mint szendvicset. $a)$ Mennyi haszna lett a büfésnek az eladott árukból a második napon? $b)$ Mennyi haszna lett volna, ha kétszer annyi szendvicset adott volna el, mint pizzát?   (14 pont)   Megoldás. $a)$ Jelöljük $a$-val egy szendvics, $b$-vel egy pizza önköltségi árát. Ha az első alkalommal $x$ darabot adott el a kereskedő mindkettőből, akkor 34%-os haszna volt, tehát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x\cdot 0\mathrm{,}3a+x\cdot 0\mathrm{,}5b}& {\displaystyle =x\left(a+b\right)\cdot 0\mathrm{,}\mathrm{34,}}\hfill \\ \hfill {\displaystyle 0\mathrm{,}16b}& {\displaystyle =0\mathrm{,}04a\mathrm{,}}\hfill \\ \hfill {\displaystyle 4b}& {\displaystyle =a\mathrm{.}}\hfill \end{array}}$ Másnap $y$ darab szendvicset és $2y$ darab pizzát adott el. Ha $p\%$-os volt a haszna, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y\cdot 0\mathrm{,}3a+2y\cdot 0\mathrm{,}5b}& {\displaystyle =\left(ya+2yb\right)\cdot \frac{p}{100}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{0\mathrm{,}3a+b}{a+2b}}& {\displaystyle =\frac{p}{100}\mathrm{.}}\hfill \end{array}}$ Felhasználva az $a=4b$ összefüggést: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{0\mathrm{,}3\cdot 4b+b}{4b+2b}}& {\displaystyle =\frac{p}{100}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{2\mathrm{,}2}{6}}& {\displaystyle =\frac{p}{100}\mathrm{,}}\hfill \\ \hfill {\displaystyle 36\mathrm{,}\dot{6}}& {\displaystyle =p\mathrm{.}}\hfill \end{array}}$ Tehát a büfésnek kb. 36,7%-os haszna volt. $b)$ Ha a kereskedő $y$ db szendvicset adott el és ez kétszer annyi, mint ahány darab pizzát eladott, akkor $\begin{array}{c}{\displaystyle y\cdot 0\mathrm{,}3a+\frac{y}{2}\cdot 0\mathrm{,}5b=\left(ya+\frac{y}{2}b\right)\cdot \frac{p}{100}\mathrm{,}\text{azaz}0\mathrm{,}3a+\frac{0\mathrm{,}5b}{2}=\left(a+\frac{b}{2}\right)\cdot \frac{p}{100}\mathrm{.}}\end{array}$ Mivel $a=4b$, azért ${\displaystyle \begin{array}{c}\hfill {\displaystyle 0\mathrm{,}3\cdot 4b+\frac{0\mathrm{,}5b}{2}=\left(4b+\frac{b}{2}\right)\cdot \frac{p}{100}\mathrm{,}1\mathrm{,}45b=4\mathrm{,}5b\cdot \frac{p}{100}\mathrm{,}\text{azaz}p=\frac{1\mathrm{,}45\cdot 100}{4\mathrm{,}5}\approx 32\mathrm{,}2.}\hfill \end{array}}$ Így a kereskedőnek kb. 32,2 % haszna lett volna.   II. 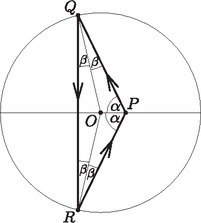rész     5. Egy 4 m átmérőjű kör alakú biliárdasztal $O$ középpontjától 0,5 méterre levő $P$ pontban van egy biliárdgolyó. A golyót úgy kell ellökni, hogy kétszeri visszaverődés után ismét a $P$ ponton haladjon át. Mekkora szöget zár be az ellökés iránya a $PO$ iránnyal?   (16 pont)   Megoldás. A $PO$-val $0^{\circ }$-os és ${180}^{\circ }$-os szöget bezáró irányok teljesítik a feltételeket. Vizsgáljuk az ezektől eltérő, $\alpha$ szöget bezáró irányt. A golyó a $P$ pontból indulva a $Q$ pontban, majd az $R$ pontban ütközve visszaérkezik a $P$ pontba. Az ütközés törvénye szerint $PQO=OQR$ és $QRO=ORP$. Az $OQR$ háromszög egyenlő szárú. A beesés és visszaverődés szöge a $\beta$ szög. A szimmetria miatt $OPQ=OPR=\alpha$, így a $PQR$ háromszögből: $\begin{array}{c}{\displaystyle 2\alpha +4\beta ={180}^{\circ }\text{és}\beta ={45}^{\circ }-\frac{\alpha }{2}\mathrm{.}}\end{array}$ Az $OPQ$ háromszögből a szinusztétel szerint: $\frac{\text{sin}\alpha }{\text{sin}\beta }=\frac{OQ}{OP}$. Az $OQ=4\cdot OP$ és a $\beta ={45}^{\circ }-\frac{\alpha }{2}$ összefüggésből:     $\begin{array}{c}{\displaystyle \frac{\text{sin}\alpha }{\text{sin}({45}^{\circ }-\frac{\alpha }{2})}=\frac{4\cdot OP}{OP}=4.}\end{array}$ Innen: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}\alpha }& {\displaystyle =4\cdot \text{sin}\left({45}^{\circ }-\frac{\alpha }{2}\right)=4\cdot \left(\frac{1}{\sqrt[]{2}}\cdot \text{cos}\frac{\alpha }{2}-\frac{1}{\sqrt[]{2}}\cdot \text{sin}\frac{\alpha }{2}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{sin}{}^2\alpha }& {\displaystyle =8{\left(\text{cos}\frac{\alpha }{2}-\text{sin}\frac{\alpha }{2}\right)}^2=8\left(\text{cos}{}^2\frac{\alpha }{2}+\text{sin}{}^2\frac{\alpha }{2}-2\text{sin}\frac{\alpha }{2}\text{cos}\frac{\alpha }{2}\right)\mathrm{.}}\hfill \end{array}}$ A trigonometrikus azonosságokat figyelembe véve: $\text{sin}{}^2\alpha =8\left(1-\text{sin}\alpha \right)$, vagyis $\text{sin}{}^2\alpha +8\text{sin}\alpha -8=0$. Ennek gyökei: ${\left(\text{sin}\alpha \right)}_1=-4+\sqrt[]{24}$, ahonnan ${\alpha }_1\approx {64}^{\circ }$, ${\left(\text{sin}\alpha \right)}_2=-4-\sqrt[]{24}$, ebből nincs megoldás, mert $\text{sin}\alpha <-1$. A keresett szög: $\alpha \approx {64}^{\circ }$.     6. Legyen egy sorozat általános tagja a következő képlettel adva: $\begin{array}{c}{\displaystyle a_n=\frac{2n^2+3n-1}{n^2+4}\mathrm{.}}\end{array}$ $a)$ Határozzuk meg a $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}{a}_n$ határértéket. $b)$ Határozzuk meg azt az $N$ küszöbszámot, amelytől kezdve a sorozat elemei a sorozat határértékétől ${10}^{-2}$-nál kisebb értékkel térnek el.  (16 pont)   Megoldás. $a)$ $\begin{array}{c}{\displaystyle A=\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{2n^2+3n-1}{n^2+4}=\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{2+\frac{3}{n}-\frac{1}{n^2}}{1+\frac{4}{n^2}}=2.}\end{array}$ $b)$ Meg kell állapítanunk, hogy milyen $n$-től kezdve lesz $|a_n-A|<\frac{1}{100}$, azaz $\begin{array}{c}{\displaystyle \left|\frac{2n^2+3n-1}{n^2+4}-2\right|<\frac{1}{100}\mathrm{.}}\end{array}$ Elvégezve az összevonást kapjuk: $\begin{array}{c}{\displaystyle \left|\frac{3n-9}{n^2+4}\right|<\frac{1}{100}\mathrm{.}}\end{array}$ Mivel $n>3$ esetén $\frac{3n-9}{n^2+4}>0$, azért a $\begin{array}{c}{\displaystyle \frac{3n-9}{n^2+4}<\frac{1}{100}}\end{array}$ egyenlőtlenséget kell vizsgálnunk. Mindkét oldalt beszorozzuk a közös nevezővel és utána rendezzük az egyenletet: $\begin{array}{c}{\displaystyle n^2-300n+904>0.}\end{array}$ Az így kapott másodfokú egyenlet megoldásai: $n_1\approx 3\mathrm{,}04$ és $n_2\approx 296\mathrm{,}96$. Vagyis a keresett sorszám: 297.     7. Az iskola konyhája két helyről szokott burgonyát rendelni 10 kg-os csomagolásban. Az A beszállítótól kétszer annyit rendelnek, mint a B-től. Az A beszállító $80\%$, a B pedig $60\%$ eséllyel szállítja a rendelt mennyiséget egy héten belül. $a)$ Mennyi az esélye, hogy egy véletlenszerűen kiválasztott 10 kg-os csomagra több, mint egy hetet kell várni? $b)$ Ha tudjuk, hogy egy héten belül leszállították a burgonyát, akkor mekkora az esélye annak, hogy A-tól rendelték? $c)$ Ha a szállítás késése esetén $10\%$ engedménnyel adják a burgonyát, és egy 10 kg-os csomag ára 800 Ft mindkét beszállítónál, akkor várhatóan hány forintot fizetnek egy 10 kg-os csomagért?  (16 pont)   Megoldás. $a)$ Legyen $x$ a B beszállítótól rendelt 10 kg-os csomagok száma. Az egy héten túli rendelések várható száma A-nál: $0\mathrm{,}2\cdot 2x$, B-nél: $0\mathrm{,}4x$, összesen $0\mathrm{,}8x$. Összes rendelés mennyisége: $3x$. $\begin{array}{c}{\displaystyle P=\frac{0\mathrm{,}2\cdot 2x+0\mathrm{,}4x}{3x}=\frac{0\mathrm{,}8}{3}\approx 0\mathrm{,}27.}\end{array}$ A keresett esély kb. 0,27. $b)$ Jelölje $A$ azt az eseményt, hogy az árut A-tól rendelték, $H$ pedig azt az eseményt, hogy egy héten belül megérkezett. Ekkor: $\begin{array}{c}{\displaystyle P\left(A\mid H\right)=\frac{P\left(AH\right)}{P\left(H\right)}=\frac{0\mathrm{,}8\cdot 2x}{3x}:\frac{0\mathrm{,}8\cdot 2x+0\mathrm{,}6x}{3x}=\frac{1\mathrm{,}6}{2\mathrm{,}2}\approx 0\mathrm{,}73.}\end{array}$ A keresett esély kb. 0,73. $c)$ $\begin{array}{c}{\displaystyle M=0\mathrm{,}27\cdot 800\cdot 0\mathrm{,}9+\left(1-0\mathrm{,}27\right)\cdot 800=778\mathrm{,}4.}\end{array}$ Vagyis várhatóan kb. 778 Ft-ot fizetnek érte.     8. 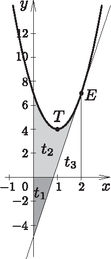Egy $y$ tengellyel párhuzamos tengelyű parabola csúcspontja a $T\left(1;4\right)$ pont, a parabola $2$ abszcisszájú pontjába húzható érintő iránytangense $6$. Határozzuk meg az $y$ tengely, a parabolaív és a parabola $2$ abszcisszájú pontjához húzható érintő által bezárt síkidom területét.  (16 pont)   Megoldás. A parabola egyenletének meghatározása: $\begin{array}{c}{\displaystyle y=a{\left(x-1\right)}^2+4=a{x}^2-2ax+a+\mathrm{4,}}\end{array}$ $y\text{'}=2ax-2a$, innen $6=y\text{'}\left(2\right)=2a$, és így $a=3$. A parabola egyenlete $y=3x^2-6x+7$. Az érintő egyenlete az $E\left(2;7\right)$ pontban $y=6x-5$, $t=t_1+t_2-t_3$, ahol a $t_2$a parabola alatti terület a $\left[0;2\right]$-ban, $t_1$ és $t_3$ pedig egy-egy háromszög területe. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t}& {\displaystyle =\frac{\frac{5}{6}\cdot 5}{2}+\underset{0}{\overset{2}{\int }}\left(3x^2-6x+7\right)dx-\frac{7(2-\frac{5}{6})}{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{25}{12}+{\left[x^3-3x^2+7x\right]}_0^2-\frac{49}{12}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{25}{12}+\left(8-12+14\right)-\frac{49}{12}=8.}\hfill \end{array}}$ Vagyis a kérdéses terület 8 területegység.       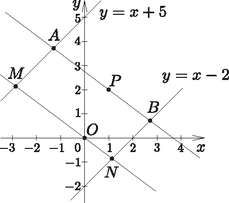9. Írjuk fel annak az egyenesnek az egyenletét, amely átmegy a $P\left(1;2\right)$ ponton, és az $x-y+5=0$, valamint az $x-y=2$ egyenesek közé eső szakasza $5$ egység.  (16 pont)   Megoldás. Legyen a feltételnek megfelelő egyenes az $AB$. Toljuk el párhuzamosan az origóba, legyen ez az $MN$ egyenes, ennek egyenlete $y=mx$. Az $y=mx$ és $y=x+5$ egyenesek metszéspontja: $M(\frac{5}{m-1};\frac{5m}{m-1})$. Az $y=mx$ és $y=x-2$ egyenesek metszéspontja: $N(\frac{-2}{m-1};\frac{-2m}{m-1})$. A feltétel szerint $MN=5$, ezért $\begin{array}{c}{\displaystyle M{N}^2=25={\left(\frac{7}{m-1}\right)}^2+{\left(\frac{7m}{m-1}\right)}^2\mathrm{.}}\end{array}$     Rendezés után a $12m^2+25m+12=0$ egyenletet kapjuk. Ennek megoldásai: $m=-\frac{3}{4}$; $m=-\frac{4}{3}$. Az ilyen meredekségű, és a $P\left(1;2\right)$ ponton átmenő egyenesek egyenlete: $4x+3y=10$, illetve $3x+4y=11$.