Cím:	A 2011. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldásairől
Szerző(k):	Fleiner Tamás
Füzet:	2012/február, 68 - 71. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Kürschák József (korábban Eötvös Loránd), Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   A 2011. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása     1. Adott pozitív egészeknek egy $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}$ végtelen sorozata, amelyre teljesül, hogy tetszőleges $k$, $\ell$ pozitív egészek esetén $a_{k+\ell }$ osztható az $a_k$ és $a_{\ell }$ számok legnagyobb közös osztójával. Mutassuk meg, hogy bármely $1\le k\le n$ esetén $a_n{a}_{n-1}\cdots a_{n-k+1}$ osztható $a_k{a}_{k-1}\cdots a_1$-gyel.   Megoldás. A binomiális együtthatók mintájára legyen $\begin{array}{c}{\displaystyle B\left(n\mathrm{,0}\right)=\mathrm{1,}\text{és}B\left(n\mathrm{,}k\right)=\frac{a_n{a}_{n-1}\cdot \text{...}\cdot a_{n-k+1}}{a_k{a}_{k-1}\cdot \text{...}\cdot a_1}\mathrm{,}\text{ha}1\le k\le n\mathrm{.}}\end{array}$ (1) Az $n$ szerinti indukcióval bizonyítjuk, hogy $B\left(n\mathrm{,}k\right)$ egész szám. A $k=0$ és $k=n$ esetekben az állításunk triviális, hisz $B\left(n\mathrm{,0}\right)=B\left(n\mathrm{,}n\right)=1$. Ez a megfigyelés egyúttal az $n=1$ esetet is bizonyítja. Tegyük fel tehát, hogy $0<k<n$, és $B\left(n\text{'}\mathrm{,}k\text{'}\right)\in \text{Z}$ teljesül minden $1\le k\text{'}\le n\text{'}<n$ értékre. Az (1) definícióból láthatjuk, hogy $\begin{array}{c}{\displaystyle B\left(n\mathrm{,}k\right)=\frac{a_n}{a_k}\cdot B\left(n-\mathrm{1,}k-1\right)=\frac{a_n}{a_{n-k}}\cdot B\left(n-\mathrm{1,}k\right)\mathrm{.}}\end{array}$ (2) A feladat feltétele szerint az $a_n$ szám osztható $a_k$ és $a_{n-k}$ legnagyobb közös osztójával. Ezért vannak olyan $x$, $y$ egész számok, amelyekre $a_{k}x+a_{n-k}y=a_n$. Ezt beírva (2)-be, ${\displaystyle \begin{array}{cc}\hfill {\displaystyle B\left(n\mathrm{,}k\right)}& {\displaystyle =\frac{a_{k}x+a_{n-k}y}{a_n}\cdot B\left(n\mathrm{,}k\right)=x\cdot \frac{a_k}{a_n}B\left(n\mathrm{,}k\right)+y\cdot \frac{a_{n-k}}{a_n}B\left(n\mathrm{,}k\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =x\cdot B\left(n-\mathrm{1,}k-1\right)+y\cdot B\left(n-\mathrm{1,}k\right)\mathrm{.}}\hfill \end{array}}$ Az indukciós feltevés szerint a jobb oldalon álló számok egészek, így $B\left(n\mathrm{,}k\right)$ is egész.  $\square$   Megjegyzések. 1. Az $\mathrm{1,2,3,}\text{...}$ sorozatra triviálisan fennáll a kívánt feltétel. A feladat erre a konkrét sorozatra éppen a a binomiális együtthatók egész tulajdonságát állítja. A kitűzött feladat tehát arra mutat rá, hogy a szorzatok hányadosának egész tulajdonsága már egy, az $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}$ sorozatról kikötött jóval gyengébb feltételből is következik. 2. Több versenyző próbálkozott annak becslésével, hogy egy $p$ prím milyen kitevőn osztja a számlálót, illetve a nevezőt. Nem nagyon nehéz megmutatni, hogy tetszőleges $q$ prímhatványnak legalább annyi többszöröse van az $a_n\mathrm{,}{a}_{n-1}\mathrm{,}\text{...}\mathrm{,}{a}_{n-k+1}$ számok között, mint az $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_{k-1}\cdots a_k$ számok között. Ebből a megfigyelésből pedig könnyen adódik a feladat megoldása.   2. Legyen $n$ pozitív egész. Jelölje $a\left(n\right)$ az olyan $n=x_1+x_2+\text{...}$ felbontások számát, ahol $x_1\le x_2\le \text{...}$ és a sorozat minden $x_i$ tagjára $x_i+1$ a $2$ pozitív egész kitevős hatványa. Jelölje $b\left(n\right)$ az olyan $n=y_1+y_2+\text{...}$ felbontások számát, ahol minden $y_i$ tag pozitív egész és az utolsó kivételével minden $y_i$-re $2\cdot y_i\le y_{i+1}$ teljesül. Igazoljuk, hogy $a\left(n\right)=b\left(n\right)$.   Megoldás. Tetszőleges olyan $n=x_1+x_2+\text{...}$ felbontást, amit az $a\left(n\right)$-ben számolunk meg, kódoljunk az alábbi módszerrel. Minden $i$-re írjuk fel az $x_i$ kettes számrendszerbeli alakját (az $i$-edik sorba $x_i$-t írva) úgy, hogy a legnagyobb helyiértéken álló számjegyek egymás alá kerüljenek. Mivel a $2^k-1$ szám kettes számrendszerbeli alakja pontosan $k$ db egyesből áll, a kapott felírásban kizárólag egyesek fognak szerepelni, és az egyesekből álló sorok hossza lefelé haladva nem csökken. Ebben a felírásban minden egyeshez egy jól meghatározott érték tartozik: ha egy egyestől jobbra $\ell$ további egyes található, akkor az adott egyes értéke pontosan $2^{\ell }$. A felírásból adódóan a kódolásból úgy olvasható ki az $x_i$, hogy az $i$-edik sorban álló egyesek értékét összeadjuk. Ha a most felírt kódolásban oszloponként adjuk össze a felírt egyesek értékét, akkor egy $n=y_1+y_2+\text{...}$ felbontást kapunk, ahol $y_i$ jelöli a jobbról az $i$-edik oszlopban álló egyesek összértékét. Világos, hogy $y_{i+1}\ge 2\cdot y_i$, hiszen $y_i$ minden egyesétől balra áll egy $y_{i+1}$-hez tartozó egyes, ami pontosan kétszer annyit ér, mint a tőle jobbra álló. Ez azt jelenti, hogy az $n=y_1+y_2+\text{...}$ felbontást $b\left(n\right)$-ben számoltuk meg. Azt kaptuk, hogy minden $a\left(n\right)$-ben leszámolt felbontáshoz tartozik egy jól meghatározott $b\left(n\right)$-ben leszámolt felbontás. A továbbiakban azt igazoljuk, hogy a fenti transzformáció kölcsönösen egyértelmű megfeleltetés a kétféle típusba tartozó felbontások között. Ezt pedig úgy mutatjuk meg, hogy minden $b\left(n\right)$-ben leszámolt $n=y_1+y_2+\text{...}$ felbontáshoz konstruálunk egy $a\left(n\right)$-ben leszámolt $n=x_1+x_2+\text{...}$ felbontást, amit a fenti transzformáció pontosan az $n=y_1+y_2+\text{...}$ felbontásba visz. Legyen tehát adott egy $b\left(n\right)$-ben leszámolt $n=y_1+y_2+\text{...}$ felbontás. A jobb szélső oszlopban helyezzünk el $y_1$ db egyest egymás felett. Ha már elkészítettünk $i$ oszlopot, akkor ezektől balra úgy konstruáljuk meg az $\left(i+1\right)$-edik oszlopot, hogy az $i$-edik oszlop minden egyese mellé balról írunk egy egyest, továbbá még $y_{i+1}-2\cdot y_i$ további egyest írunk ezen egyesek fölé. Ez $y_{i+1}\ge 2\cdot y_i$ miatt mindig megtehető. Világos, hogy ha most minden egyesnek a fent definiált értéket adjuk, akkor a $j$-edik oszlopbeli egyesek összértéke pontosan $y_i$ lesz minden értelmes $i$-re. Ha pedig a felírt egyeseket soronként olvassuk ki kettes számrendszerbeli számokként, akkor ezen számok az $n$-nek egy $a\left(n\right)$-ben leszámolt $x_1+x_2+\text{...}$ felbontását adják, amit (a konstrukció miatt) a fent leírt transzformáció pontosan az $n=y_1+y_2+\text{...}$ felbontásba visz. Mi pedig éppen ezt akartuk bizonyítani.  $\square$   Megjegyzés. A megoldás rámutat arra is, hogyan keletkezett a feladat. A jól ismert Ferrers-diagram konjugálásának mintájára teremtünk bijekciót a kétféle partíciótípus között azzal a különbséggel, hogy míg a Ferrers-diagramban minden jel értéke $1$, ez a feladatban egy kettőhatvány, ami a diagramból egyértelműen kikövetkeztethető. Ha tehát Ferrers-diagramként (azaz ,,egyes számrendszerben'') értelmezzük az $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle 1}\hfill \\ \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill \\ \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill \\ \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 1}\hfill \end{array}}}\end{array}$ reprezentációt, akkor az a $14=1+3+3+7$ partíciót jelenti, aminek konjugáltja a $\begin{array}{c}{\displaystyle 14=1+1+1+1+3+3+4.}\end{array}$ Ugyanez a diagram a feladatbeli kódolás szerint az $a\left(n\right)$-ben leszámolt $142=1+7+7+127$ partíciót kódolja, amihez a $b\left(n\right)$-ben leszámolt $\begin{array}{c}{\displaystyle 142=1+2+4+8+18+36+73}\end{array}$ partíció tartozik.   3. Adott a síkon $2n$ pont és $3n$ egyenes. Bizonyítsuk be, hogy van a síkon olyan $P$ pont, hogy $P$-nek a $3n$ egyenestől való távolságainak összege kisebb, mint $P$-nek a $2n$ ponttól való távolságainak összege.   Megjegyzés. A megoldáshoz vezető alábbi ötletre sokan rájöttek. Ha igaz az állítás, akkor annak úgy is teljesülnie kell, ha az adott egyenesek mindegyike ugyanazon az $O$ ponton halad át, és ugyanez a metszéspont van $2n$ multiplicitással megadva. Ha ekkor egy $O$-tól különböző $P$ pont rendelkezik a kívánt tulajdonsággal, akkor az $OP$ félegyenes bármely pontja ilyen tulajdonságú. Márpedig, ha ,,kellően messziről'' nézünk rá a síkra, akkor az egyenesek és a pontok ,,nagyon közel'' lesznek ehhez az állapothoz. Az utolsó ötlet pedig az, hogy ha nagyon sok egyenes van adva, és azok egy szabályos $6n$ oldalú sokszög átmérői, akkor $P$-nek az egyenesektől mért össztávolsága ,,nagyjából'' arányos lesz az $OP$ távolsággal. Tehát ha az állítás igaz, akkor annak már egy véletlenül választott $P$ pontra is pozitív valószínűséggel kell teljesülnie. Ezeket a gondolatokat bontjuk ki az alábbi megoldásban.   Megoldás. Válasszunk egy olyan $k$ kört a síkon, amiből a $3n$ egyenes mindegyike olyan húrt metsz ki, amihez legalább $(1-\frac{1}{10n})\pi$ nagyságú középponti szög tartozik. Könnyen látható, hogy létezik ilyen kör: válasszuk a $k$ kör $O$ középpontját tetszőlegesen, sugara pedig $\begin{array}{c}{\displaystyle r=d\cdot \text{cos}\left(\left(\frac{10n-1}{20n}\right)\pi \right)}\end{array}$ legyen, ahol $d$ az adott egyeneseknek az $O$-tól mért távolságai közül a legnagyobb. 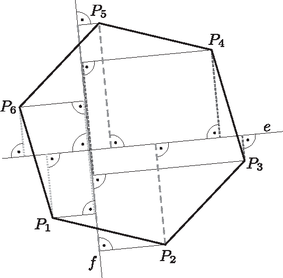Ha $H$ egy, a $k$ körbe írt szabályos hatszög és $e$ a megadott egyenesek egyike, akkor azt mondjuk, hogy $H$ jó $e$-hez, ha $H$-nak $3-3$ csúcsa esik $e$ mindkét partjára, azaz $e$ a $H$ két átellenes oldalát metszi. A $k$ választása folytán az olyan szabályos hatszögek csúcsai, amik nem jók $e$-hez a $k$ körnek hat ívét alkotják, és mindegyik ívhez legfeljebb $\frac{\pi }{10n}$ nagyságú középponti szög tartozik. Mivel $6\cdot 3n$ ilyen ív nem fedheti a $k$ kört, ezért található olyan $k$-ba írt $P_1{P}_2{P}_3{P}_4{P}_5{P}_6$ szabályos hatszög, ami a megadott $3n$ egyenes mindegyikéhez jó. Sőt, még az is feltehető, hogy a $3n$ egyenes egyike sem merőleges a $P_1{P}_2{P}_3{P}_4{P}_5{P}_6$ hatszög egyetlen oldalára sem. Azt állítjuk, hogy a $P_1$, $P_2$, $P_3$, $P_4$, $P_5$, $P_6$ pontok valamelyike rendelkezik a feladatban leírt tulajdonsággal. Ehhez elegendő megmutatni, hogy e hat pontnak a $2n$ megadott ponttól vett távolságösszege több, mint a $3n$ egyenestől vett távolságösszege, hiszen ekkor nem lehetséges hogy mindegyik $P_i$-nek a pontoktól mért távolságösszege legalább akkora legyen, mint az egyenesektől való. Legyen tehát $X$ a megadott pontok valamelyike. A háromszög-egyenlőtlenség miatt $\begin{array}{c}{\displaystyle |\overline{P_{1}X}|+|\overline{P_{4}X}|\ge |\overline{P_1{P}_4}|=2r\mathrm{,}}\end{array}$ hisz $P_1$ és $P_4$ az $r$ sugarú $k$ kör átellenes pontjai. Hasonló okból $\begin{array}{c}{\displaystyle |\overline{P_{2}X}|+|\overline{P_{5}X}|\ge |\overline{P_2{P}_5}|=2r\text{és}|\overline{P_{3}X}|+|\overline{P_{6}X}|\ge |\overline{P_3{P}_6}|=2r\mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle |\overline{P_{1}X}|+|\overline{P_{2}X}|+|\overline{P_{3}X}|+|\overline{P_{4}X}|+|\overline{P_{5}X}|+|\overline{P_{6}X}|\ge 6r\mathrm{.}}\end{array}$ A megadott pontok mindegyikére összeadva a fenti becslést azt kapjuk, a $P_i$ pontoknak a $2n$ megadott ponttól vett távolságösszege legalább $12rn$. A bizonyítás befejezéséhez az alábbiakban azt igazoljuk, hogy a $P_i$ pontoknak az egyenesektől mért távolságösszege kisebb $12rn$-nél. Legyen $e$ a megadott $3n$ egyenes valamelyike. Feltehetjük, hogy $e$ a $P_1{P}_6$ és $P_3{P}_4$ oldalakat metszi, azaz $e$ egyik partján a $P_1$, $P_2$ és $P_3$, míg a másikon a $P_4$, $P_5$ és $P_6$ pontok vannak. Világos, hogy a $P_1$ és $P_6$ pontoknak az $e$ egyenestől mért távolságainak összege megegyezik a $\overline{P_1{P}_6}$ szakasznak egy $e$-re merőleges $f$ egyenesre vett merőleges vetületének hosszával.   Hasonlóan, a $P_2$ és $P_5$, illetve a $P_3$ és $P_4$ pontok $e$-től mért távolságösszege a $\overline{P_2{P}_5}$, illetve a $\overline{P_3{P}_4}$ szakaszok $f$-re vett merőleges vetületének hossza. Márpedig a merőleges vetület hossza sosem nagyobb a vetített szakaszénál, jelen esetben pedig szigorúan kisebb annál, ugyanis a hatszöget úgy választottuk, hogy $P_1{P}_6$ nem merőleges $e$-re. Tehát a kérdéses távolságösszeg szigorúan kisebb, mint e három szakasz összhossza, azaz $|\overline{P_1{P}_6}|+|\overline{P_2{P}_5}|+|\overline{P_3{P}_4}|=r+2r+r=4r$, hiszen a szabályos hatszög oldalhossza megegyezik a köré írt kör sugarával, míg az átellenes csúcsokat összekötő húr a $k$ kör átmérője. Azt kaptuk, hogy a $P_i$-knek a megadott $3n$ egyenestől a távolságösszege kisebb, mint $3n\cdot 4r=12rn$. Nekünk pedig pontosan ezt kellett bizonyítanunk.  $\square$   Megjegyzés. A feladatbelinél erősebb állítás is igaz. Ha nem csak egy szabályos hatszög csúcsaival dolgozunk, hanem egy megfelelően nagy $k$ körön egyenletes eloszlással választott véletlen pontra számítjuk ki a kérdéses távolságösszegek várható értékeit (ehhez a $k$ kör mentén kell integrálni), akkor az is könnyen igazolható, hogy tetszőleges $n$ pont és $k$ egyenes esetén, ahol $k<\frac{\pi }{2}\cdot n$, mindig létezik olyan $P$ pont a síkon, hogy $P$-nek a pontoktól vett távolságösszege legalább akkora, mint $P$-nek az egyenesektől mért távolságainak összege.