Gimnáziumi matematika órákon sokan találkozhatnak a következő, vagy ehhez hasonló példákkal. A feladat rendszerint a ,,függvények, függvényábrázolások'' témakör kapcsán kerül terítékre, hiszen grafikus megoldása kézenfekvő. Azonban ha hagyjuk, e feladat messze kivezet bennünket a grafikus egyenletmegoldás témaköréből.

A megoldás grafikus úton egyszerű: Legyen

$\begin{array}{c}{\displaystyle f\left(x\right):=\left|\left|\left|\left||x|-2^3\right|-2^2\right|-2\right|-1\right|}\end{array}$

és

$\begin{array}{c}{\displaystyle g\left(x\right):=||\text{...}||x|-1|-1|-1|-1|-1|-1|-1|-1|-1|-1|-1|-1|-1|-1|-1|\mathrm{.}}\end{array}$

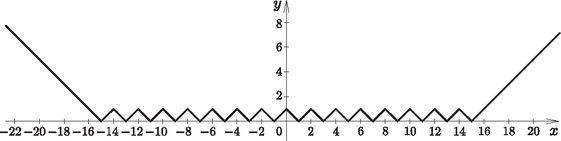
Ekkor $f\left(x\right)$-et és $g\left(x\right)$-et koordinátarendszerben ábrázolva ugyanazt a függvényképet kapjuk, tehát $f\left(x\right)=g\left(x\right)$ minden $x$-re (1. ábra).

 

 

1. ábra. $f\left(x\right)$ és $g\left(x\right)$ közös képe

 

A feladatban szereplő függvények grafikonját nézve felmerül a kérdés: Vajon igaz-e minden $n$-re, hogy

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle f\left(x\right)}& {\displaystyle =\left|\left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2\right|-1\right|\text{és}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle g\left(x\right)}& {\displaystyle =||\text{...}|||x|\underset{\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">(</mo><mrow><msup><mrow><mn>2</mn></mrow><mrow><mi>n</mi><mo stretchy="false">+</mo><mn>1</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>1</mn></math> db 1-es)}}{\overset{}{\underbrace{-1|-1|-\text{...}|-1|}}}}\hfill & \text{(<mn>2</mn>)}\end{array}}$

ugyanaz a függvény, és e függvény grafikonja is csak egyes ,,fogakból'' áll? A következőkben ezekre a kérdésekre keresünk választ.
Legyenek tehát $f\left(x\right)$ és $g\left(x\right)$ az (1) és (2) képletek alapján megadott függvények. A továbbiakhoz először elevenítsük fel, hogyan bontunk fel (értékelünk ki) egy abszolút értékes kifejezést. Legyen $a\mathrm{,}b\ge 0$ egész. $|a+b|=a+b$, és ha $a-b\ge 0$, akkor $|a-b|=a-b$, azonban ha $a-b<0$, akkor $|a-b|=-a+b$.

 

1. $f\left(x\right)=g\left(x\right)$ bizonyítása. Vizsgáljuk a függvényértékeket először $|x|>2^{n+1}$-re. A feltétel miatt az abszolút érték felbontás szabályai alapján

${\displaystyle \begin{array}{cc}\hfill {\displaystyle f\left(x\right)}& {\displaystyle =\left||x|-2^n-2^{n-1}-\text{...}-2-1\right|=|x|-2^n-2^{n-1}-\text{...}-2-1=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =|x|-\left(2^{n+1}-1\right)\mathrm{,}}\hfill \end{array}}$

hiszen $2^0$-tól $2^n$-ig a 2-hatványok összege $2^{n+1}-1$, $|x|$ pedig ennél nagyobb. Ugyanígy

$\begin{array}{c}{\displaystyle g\left(x\right)=\left||x|-1-1-\text{...}-1-1\right|=|x|-\left(2^{n+1}-1\right)\mathrm{,}}\end{array}$

tehát ekkor valóban $f\left(x\right)=g\left(x\right)$.
Most vizsgáljuk $|x|\le 2^{n+1}$-re: ez már kicsit hosszabb lesz. Először azt mutatjuk meg, hogy ilyenkor $f\left(x\right)\le 1$ és $g\left(x\right)\le 1$, majd azt, hogy ebből következően tényleg egyenlőek. A bizonyítás első részében vegyük ismét az abszolút érték felbontás nélküli alakokat. Tekintsük külön, először $f\left(x\right)$-et, majd $g\left(x\right)$-et, azt szeretnénk belátni, hogy

$\begin{array}{c}{\displaystyle f\left(x\right)=\left|\left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2\right|-1\right|\le 1.}\end{array}$

Bizonyítsunk teljes indukcióval. $i=n$-re az állítás teljesül: $\left||x|-2^n\right|\le 2^n$, mert $|x|\le 2^{n+1}$. Indukciós feltétel: ha $i=k$-ra

$\begin{array}{c}{\displaystyle \left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2^{k+1}\right|\le 2^{k+1}\mathrm{,}}\end{array}$

(3)

akkor

$\begin{array}{c}{\displaystyle \left|\left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2^{k+1}\right|-2^k\right|\le 2^k\left(\text{ahol }0\le k\le n\right)\mathrm{.}}\end{array}$

Bizonyítás. $\left|\left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2^{k+1}\right|-2^k\right|$ maximális akkor lehet, ha

$\begin{array}{c}{\displaystyle \left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2^{k+1}\right|-2^k}\end{array}$

(4)

minimális, vagy maximális.
Mivel a (3) indukciós feltétel teljesül, és felveszi a $2^{k+1}$ értéket (pl. $x=2^{n+1}$-re), azért ha (4) maximális, akkor

$\begin{array}{c}{\displaystyle \left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2^{k+1}\right|-2^k=2^{k+1}-2^k=2^k\mathrm{,}}\end{array}$

ha pedig (4) minimális, akkor

$\begin{array}{c}{\displaystyle \left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2^{k+1}\right|-2^k=0-2^k=-2^k\mathrm{.}}\end{array}$

Így

$\begin{array}{c}{\displaystyle \left|\left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2^{k+1}\right|-2^k\right|\le 2^k\mathrm{.}}\end{array}$

Az előzőek miatt $f\left(x\right)\le 2^0=1$ teljesül a vizsgált intervallumban.
Bizonyítsuk ugyanezt $g\left(x\right)$-re. Nézzük végig azt a folyamatot, ahogy $g\left(x\right)$ készül. Vesszük $x$ abszolút értékét, majd levonunk 1-et és vesszük annak az abszolút értékét. Ezután ismét levonunk 1-et, és abszolút értéket képzünk, $\text{...}$ stb. Állítsuk meg ezt a folyamatot ott, ahol

$\begin{array}{c}{\displaystyle ||\text{...}|||x|\underset{\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>k</mi></math> db egyes}}{\overset{}{\underbrace{-1|-1|-\text{...}|-1|}}}=1\left(0\le k\le 2^{n+1}-1\right)\mathrm{.}}\end{array}$

Ilyen helyzet biztosan előáll valamikor, hiszen $|x|\le 2^{n+1}$, és $2^{n+1}-1$ darab 1-est vonunk le összesen. Ha ekkor még nem vagyunk $g\left(x\right)$ képzésének végén, akkor az abszolút értékek alakulása:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle ||\text{...}|||x|\underset{\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>k</mi><mo stretchy="false">+</mo><mn>1</mn></math> db egyes}}{\overset{}{\underbrace{-1|-1|-\text{...}|-1|}}}}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle ||\text{...}|||x|\underset{\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>k</mi><mo stretchy="false">+</mo><mn>2</mn></math> db egyes}}{\overset{}{\underbrace{-1|-1|-\text{...}|-1|}}}}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle ||\text{...}|||x|\underset{\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>k</mi><mo stretchy="false">+</mo><mn>3</mn></math> db egyes}}{\overset{}{\underbrace{-1|-1|-\text{...}|-1|}}}}& {\displaystyle =\mathrm{0,}\text{...}\text{stb.}}\hfill \end{array}}$

Látható, hogy innentől $g\left(x\right)$ nem lesz nagyobb 1-nél. Azonban, mint láttuk, $g\left(x\right)$ képzése közben egyszer biztosan eléri az 1 értéket, tehát $g\left(x\right)\le 1$.
Beláttuk, hogy $|x|\le 2^{n+1}$ esetben $f\left(x\right)\le 1$ és $g\left(x\right)\le 1$. Elérkeztünk a bizonyítás második részéhez. Szeretnénk az előbbiek felhasználásával megmutatni, hogy $f\left(x\right)=g\left(x\right)$. A könnyebb átláthatóság kedvéért alakítsuk át az $f\left(x\right)$ és $g\left(x\right)$ függvényeket. A szabályok szerint bontsuk fel $f\left(x\right)$-ben és $g\left(x\right)$-ben az abszolút érték jeleket, kivéve $x$-ét és az utolsót:

ahol a $\pm$ előjel $+$, vagy $-$ úgy, ahogy a felbontás műveletét végezzük.
Tekintsük $f\left(x\right)$-nek az $\left(1\text{'}\right)$ szerint felbontott alakját. Jelölje $A\left(x\right)$ az $|x|$-hez hozzáadott és kivont számok összegét, azaz

$\begin{array}{c}{\displaystyle A\left(x\right)=\pm 2^n\pm 2^{n-1}\pm \text{...}\pm 2\pm \mathrm{1,}}\end{array}$

ahol az egyes tagok előjelei az abszolút érték felbontások esetén alakulnak, tehát $|x|$ nagyságától függenek. Ekkor tehát $f\left(x\right)=\left||x|-A\left(x\right)\right|$. Az $A\left(x\right)$ páratlan szám, hiszen 2-hatványok összege és különbsége $\pm 1\left(=\pm 2^0\right)$.
Ugyanígy tekintsük $g\left(x\right)$-nek a $\left(2\text{'}\right)$ szerint felbontott alakját. Jelölje $B\left(x\right)$ az $|x|$-hez hozzáadott és kivont számok összegét, vagyis

$\begin{array}{c}{\displaystyle B\left(x\right)=\pm 1\pm 1\pm \text{...}\pm 1\pm \mathrm{1,}}\end{array}$

ahol az egyes tagok előjelei az abszolút érték felbontások esetén alakulnak, tehát $|x|$ nagyságától függenek. Ekkor tehát $g\left(x\right)=\left||x|-B\left(x\right)\right|$. $B\left(x\right)$ is páratlan szám, hiszen $2^{n+1}-1$ darab, azaz páratlan darab egyes összege vagy különbsége.
Így $f\left(x\right)$-et és $g\left(x\right)$-et egyszerűbb alakra hoztuk, használjuk ezt tovább. Most $|x|$-et alakítjuk át úgy, hogy a bizonyítás szemléletes legyen: írjuk át $\left[|x|\right]+\left\{|x|\right\}$ alakba (ahol $\left[|x|\right]$ az $|x|$ egész részét, $\left\{|x|\right\}$ az $|x|$ törtrészét jelenti). Így

${\displaystyle \begin{array}{cc}\hfill {\displaystyle f\left(x\right)}& {\displaystyle =\left||x|-A\left(x\right)\right|=\left|\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)\right|}\hfill \\ \hfill {\displaystyle }\\ \hfill {\displaystyle \text{és}}\\ \hfill {\displaystyle g\left(x\right)}& {\displaystyle =\left||x|-B\left(x\right)\right|=\left|\left[|x|\right]+\left\{|x|\right\}-B\left(x\right)\right|\mathrm{.}}\hfill \end{array}}$

Bontsuk fel a legkülső abszolút érték jeleket $f\left(x\right)$-ben és $g\left(x\right)$-ben is. Ezt kétszer két esetre bontjuk $f\left(x\right)$ és $g\left(x\right)$ esetében is, attól függően, hogy $\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)$ nemnegatív, vagy negatív, és attól függően, hogy $\left\{|x|\right\}=0$, vagy $\left\{|x|\right\}\ne 0$.

(1)

Ha $\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)\ge 0$, akkor $f\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)|\le 1$ miatt $0\le \left[|x|\right]+\left\{|x|\right\}-A\left(x\right)\le 1$. Ekkor tehát $0-\left\{|x|\right\}\le \left[|x|\right]-A\left(x\right)\le 1-\left\{|x|\right\}$.

$\left(a\right)$

Ha $\left\{|x|\right\}=0$, akkor $0\le \left[|x|\right]-A\left(x\right)\le 1$. $\left[|x|\right]$ és $A\left(x\right)$ egész számok, ezért $\left[|x|\right]-A\left(x\right)$ is egész, ebből következik, hogy $\left[|x|\right]-A\left(x\right)=0$ vagy 1. Mivel $A\left(x\right)$ páratlan, azért $\begin{array}{c}{\displaystyle \left[|x|\right]-A\left(x\right)=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \mathrm{0,}}& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">|</mo><mi>x</mi><mo stretchy="false">|</mo></math> páratlan,}}\hfill \\ \hfill {\displaystyle \mathrm{1,}}& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">|</mo><mi>x</mi><mo stretchy="false">|</mo></math> páros.}}\hfill \end{array}}}\end{array}$ Így $f\left(x\right)=0$, ha $|x|$ páratlan, és $f\left(x\right)=1$, ha $|x|$ páros.

$\left(b\right)$

Ha $\left\{|x|\right\}\ne 0$, akkor $0-\left\{|x|\right\}\le \left[|x|\right]-A\left(x\right)\le 1-\left\{|x|\right\}$. Itt $\left[|x|\right]$ és $A\left(x\right)$ egész számok, ezért $\left[|x|\right]-A\left(x\right)$ is egész, ebből következik, hogy $\left[|x|\right]-A\left(x\right)=0$. Így $\begin{array}{c}{\displaystyle f\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)|=|0+\left\{|x|\right\}|=\left\{|x|\right\}\mathrm{.}}\end{array}$

(2)

Ha $\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)<0$, akkor $f\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)|\le 1$ miatt $0<A\left(x\right)-\left[|x|\right]-\left\{|x|\right\}\le 1$. Ekkor tehát $\left\{|x|\right\}<A\left(x\right)-\left[|x|\right]\le 1+\left\{|x|\right\}$.

$\left(a\right)$

Ha $\left\{|x|\right\}=0$, akkor $0<A\left(x\right)-\left[|x|\right]\le 1$. Az $\left[|x|\right]$ és $A\left(x\right)$ egész számok, ezért $A\left(x\right)-\left[|x|\right]$ is egész, ebből következik, hogy $A\left(x\right)-\left[|x|\right]=1$. Így $f\left(x\right)=1$.

$\left(b\right)$

Ha $\left\{|x|\right\}\ne 0$, akkor $\left\{|x|\right\}<A\left(x\right)-\left[|x|\right]\le 1+\left\{|x|\right\}$. Az $\left[|x|\right]$ és $A\left(x\right)$ egész számok, ezért $A\left(x\right)-\left[|x|\right]$ is egész, ebből következik, hogy $A\left(x\right)-\left[|x|\right]=1$. Így $\begin{array}{c}{\displaystyle f\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-A\left(x\right)|=A\left(x\right)-\left[|x|\right]-\left\{|x|\right\}=1-\left\{|x|\right\}\mathrm{.}}\end{array}$

Hasonlóan

(1)

Ha $\left[|x|\right]+\left\{|x|\right\}-B\left(x\right)\ge 0$, akkor $g\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-B\left(x\right)|\le 1$ miatt $0\le \left[|x|\right]+\left\{|x|\right\}-B\left(x\right)\le 1$, ekkor tehát $0-\left\{|x|\right\}\le \left[|x|\right]-B\left(x\right)\le 1-\left\{|x|\right\}$.

$\left(a\right)$

Ha $\left\{|x|\right\}=0$, akkor $0\le \left[|x|\right]-B\left(x\right)\le 1$. $\left[|x|\right]$ és $B\left(x\right)$ egész számok, ezért $\left[|x|\right]-B\left(x\right)$ is egész, ebből következik, hogy $\left[|x|\right]-B\left(x\right)=0$, vagy 1.

Mivel $B\left(x\right)$ páratlan, azért $\left[|x|\right]-B\left(x\right)=0$, ha $|x|$ páratlan, és $\left[|x|\right]-B\left(x\right)=1$, ha $|x|$ páros. Így $g\left(x\right)=0$, ha $|x|$ páratlan, és $g\left(x\right)=1$, ha $|x|$ páros.

$\left(b\right)$

Ha $\left\{|x|\right\}\ne 0$, akkor $0-\left\{|x|\right\}\le \left[|x|\right]-B\left(x\right)\le 1-\left\{|x|\right\}$. $\left[|x|\right]$ és $B\left(x\right)$ egész számok, ezért $\left[|x|\right]-B\left(x\right)$ is egész, ebből következik, hogy $\left[|x|\right]-B\left(x\right)=0$. Így $\begin{array}{c}{\displaystyle g\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-B\left(x\right)|=|0+\left\{|x|\right\}|=\left\{|x|\right\}\mathrm{.}}\end{array}$

(2)

Ha $\left[|x|\right]+\left\{|x|\right\}-B\left(x\right)<0$, akkor $g\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-B\left(x\right)|\le 1$ miatt $0<B\left(x\right)-\left[|x|\right]-\left\{|x|\right\}\le 1$. Ekkor tehát $\left\{|x|\right\}<B\left(x\right)-\left[|x|\right]\le 1+\left\{|x|\right\}$.

$\left(a\right)$

Ha $\left\{|x|\right\}=0$, akkor $0<B\left(x\right)-\left[|x|\right]\le 1$. $\left[|x|\right]$ és $B\left(x\right)$ egész számok, ezért $B\left(x\right)-\left[|x|\right]$ is egész, ebből következik, hogy $B\left(x\right)-\left[|x|\right]=1$; így $g\left(x\right)=1$.

$\left(b\right)$

Ha $\left\{|x|\right\}\ne 0$, akkor $\left\{|x|\right\}\le B\left(x\right)-\left[|x|\right]\le 1+\left\{|x|\right\}$. $\left[|x|\right]$ és $B\left(x\right)$ egész számok, ezért $B\left(x\right)-\left[|x|\right]$ is egész, ebből következik, hogy $B\left(x\right)-\left[|x|\right]=1$. Így $\begin{array}{c}{\displaystyle g\left(x\right)=|\left[|x|\right]+\left\{|x|\right\}-B\left(x\right)|=B\left(x\right)-\left[|x|\right]-\left\{|x|\right\}=1-\left\{|x|\right\}\mathrm{.}}\end{array}$

Az $\left(1a\right)$, $\left(1b\right)$, $\left(2a\right)$, $\left(2b\right)$ esetek eredményeit $f\left(x\right)$-re és $g\left(x\right)$-re megnézve látjuk, hogy minden esetben $f\left(x\right)=g\left(x\right)$. (Mindegyik eset bizonyításakor felhasználtuk az előző eredményt, miszerint $f\left(x\right)\le 1$ és $g\left(x\right)\le 1$.)

 

2. A továbbiakban azt mutatjuk meg, hogy ha $|x|<2^{n+1}-1$, akkor $f\left(x\right)$ és $g\left(x\right)$ grafikonja egyes ,,fogakból'' áll.
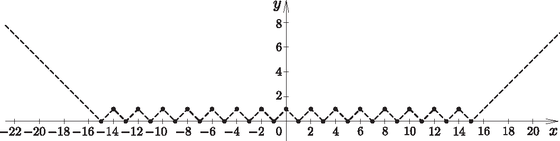
Az előbbi esetszétválasztásnál láttuk, hogy ha $|x|$ egész és páros, akkor $f\left(x\right)=g\left(x\right)=1$, ha $|x|$ egész és páratlan, akkor $f\left(x\right)=g\left(x\right)=0$. Ezeket a pontokat, vagyis az egész értékeknek megfelelőket ennek alapján már ábrázolhatjuk (2. ábra).

 

 

2. ábra

 

E pontokat csak az előbb részeredményekként kapott $1-\left\{|x|\right\}$ vagy $\left\{|x|\right\}$ függvények grafikonrészletei ,,köthetik össze''. Mivel ha $|x|$ egész, akkor felváltva páros, vagy páratlan, így az $1-\left\{|x|\right\}$ és $\left\{|x|\right\}$ függvények grafikonrészletei is felváltva jelennek meg, hiszen két szomszédos pontot egyféleképpen köthetünk össze ezen grafikonrészletek segítségével, egymáshoz viszonyított helyzetük szerint. Tehát $f\left(x\right)=g\left(x\right)$ egyes fogakból áll.

 

3. Most, hogy minden $k\left(x\right)=\left|\left|\left|\text{...}\left|\left||x|-2^n\right|-2^{n-1}\right|-\text{...}\right|-2\right|-1\right|$ függvényre láttuk, hogy a görbéje hogyan néz ki, további általánosítás lehetősége jelenik meg.
Mi a feltétele annak, hogy egy $h\left(x\right)=\left|\left|\text{...}\left|\left||x|-a_n\right|-a_{n-1}\right|-\text{...}\right|-a_0\right|$ alakú függvény (ahol az $a_i$ számok pozitív egészek) grafikonja csak egyes fogakból álljon? Megmutatjuk, hogy ennek szükséges és elégséges feltétele az, hogy minden $0\le m\le n$-re

$\begin{array}{c}{\displaystyle a_m-1\le \sum _{i=0}^{m-1}{a}_i\mathrm{,}\text{azaz}{a}_m-\sum _{i=0}^{m-1}{a}_i\le 1}\end{array}$

teljesüljön. A bizonyítást ismét kétfelé bontjuk aszerint, hogy $|x|>{\sum }_{i=0}^n{a}_i$ vagy $|x|\le {\sum }_{i=0}^n{a}_i$.
Az első esetben könnyen láthatjuk, hogy $h\left(x\right)=|x|-{\sum }_{i=0}^n{a}_i$.
Tegyük föl ezután, hogy $|x|\le {\sum }_{i=0}^n{a}_i$. Az előző feladathoz hasonlóan itt is teljes indukcióval bizonyítunk, azonban az indukciós feltétel kicsit változik. Hogy lássuk, miért változik, először nézzük meg, hogyan alakul $h\left(x\right)$ maximális értéke: $\left||x|-a_n\right|$ akkor lehet maximális, ha $|x|-a_n$ a legnagyobb vagy a legkisebb.
Az $|x|$-re érvényes feltétel miatt nyilván $\left||x|-a_n\right|$ akkor maximális, ha $|x|=0$, vagy ha $|x|={\sum }_{i=0}^n{a}_i$. Amennyiben $|x|=0$, akkor $\left||x|-a_n\right|=a_n$, ha pedig $|x|={\sum }_{i=0}^n{a}_i$, akkor $\left||x|-a_n\right|={\sum }_{i=0}^n{a}_i-a_n$. Tehát

$\begin{array}{c}{\displaystyle 0\le \left||x|-a_n\right|\le a_n\mathrm{,}\text{vagy}0\le \left||x|-a_n\right|\le \sum _{i=0}^n{a}_i-a_n\mathrm{.}}\end{array}$

Ugyanígy tovább:
Ha $\left||x|-a_n\right|-a_{n-1}<0$, akkor $\left|\left||x|-a_n\right|-a_{n-1}\right|\le a_{n-1}$.
Ha $\left||x|-a_n\right|-a_{n-1}\ge 0$, akkor
$\begin{array}{c}\end{array}$ ha $\left||x|-a_n\right|\le {\sum }_{i=0}^n{a}_i-a_n$, akkor

$\begin{array}{c}{\displaystyle \left|\left||x|-a_n\right|-a_{n-1}\right|\le \sum _{i=0}^n{a}_i-a_n-a_{n-1}\mathrm{,}}\end{array}$

$\begin{array}{c}\end{array}$ ha $\left||x|-a_n\right|\le a_n$, akkor $\left|\left||x|-a_n\right|-a_{n-1}\right|\le a_n-a_{n-1}$.
Az indukciós lépés a következő lesz. Ha teljesül, hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left|\left|\text{...}\left|\left||x|-a_n\right|-a_{n-1}\right|-\text{...}\right|-a_{k+1}\right|}& {\displaystyle \le a_{k+1}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_{k+2}-a_{k+1}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_{k+3}-a_{k+2}-a_{k+1}\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le {\sum }_{i=0}^n{a}_i-a_n-a_{n-1}-\text{...}-a_{k+1}\mathrm{,}}\hfill \end{array}}$

akkor fennáll, hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left|\left|\text{...}\left|\left||x|-a_n\right|-a_{n-1}\right|-\text{...}\right|-a_k\right|}& {\displaystyle \le a_k\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_{k+1}-a_k\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_{k+2}-a_{k+1}-a_k\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le {\sum }_{i=0}^n{a}_i-a_n-a_{n-1}-\text{...}-a_k\mathrm{.}}\hfill \end{array}}$

Tehát $h\left(x\right)$-re teljesül, hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle h\left(x\right)}& {\displaystyle \le a_0\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_1-a_0\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_2-a_1-a_0\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le {\sum }_{i=0}^n{a}_i-a_n-a_{n-1}-\text{...}-a_0\mathrm{.}}\hfill \end{array}}$

Ahhoz, hogy $h\left(x\right)\le 1$ igaz legyen, annak kell teljesülnie, hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle h\left(x\right)}& {\displaystyle \le a_0\le \mathrm{1,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_1-a_0\le \mathrm{1,}}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le a_2-a_1-a_0\le \mathrm{1,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle \text{vagy }}& {\displaystyle \le {\sum }_{i=0}^n{a}_i-a_n-a_{n-1}-\text{...}-a_0\le 1.}\hfill \end{array}}$

Vagyis teljesülnie kell annak ‐ és ez a feltétel egyben elégséges is ‐ hogy

${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_0}& {\displaystyle \le \mathrm{1,}}\hfill \\ \hfill {\displaystyle a_1-a_0}& {\displaystyle \le \mathrm{1,}}\hfill \\ \hfill {\displaystyle a_2-a_1-a_0}& {\displaystyle \le \mathrm{1,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle {\sum }_{i=0}^n{a}_i-a_n-a_{n-1}-\text{...}-a_0}& {\displaystyle \le 1.}\hfill \end{array}}$

Ez pedig éppen a korábban kimondott bizonyítandó feltétel, vagyis hogy

$\begin{array}{c}{\displaystyle a_m-\sum _{i=0}^{m-1}{a}_i\le 1.}\end{array}$

Tehát $h\left(x\right)$ valóban legfeljebb 1.
Ekkor $h\left(x\right)$-et $h\left(x\right)=\left|\left[|x|\right]+\left\{|x|\right\}-C\left(x\right)\right|$ alakba átírva a bizonyítás a második feladatban látottak szerint fejeződik be. Tehát ha $a_m-{\sum }_{i=0}^{m-1}{a}_i\le 1$ (ahol $0\le m\le n$) teljesül, akkor $h\left(x\right)$ csak egyes fogakból áll. Mi következik még ebből a feltételből? Nézzük $h\left(x\right)$ utolsó, nem nulla $\left(a_0\right)$ tagját. Erre a feltétel szerint igaz, hogy $a_0\le 1$. Tehát $a_0=1$. Ekkor viszont $a_1\le 1+a_0=2$.
Ugyanígy, ha $a_k\le 1+a_{k-1}+a_{k-2}+\text{...}+a_0$, ahol $a_i=2^i$ ($0\le i\le k-1$), akkor $a_k\le 1+2^k-1=2^k$, vagyis $h\left(x\right)$  $k$-adik tagja nem lehet nagyobb $2^k$-nál. Ebből látszik, hogy az első feladatban szereplő $f\left(x\right)$ függvény paraméterei a megengedett korlátozásokhoz képest a lehető leggyorsabban növekednek, hiszen ott minden $k$-ra $a_k=2^k$.
Befejezésül és az előbbiek alkalmazásaként egy, a kiindulási példához hasonló feladat:
Igazoljuk, hogy

$\begin{array}{c}{\displaystyle ||\text{...}|||x|-13|-8|-5|-3|-2|-1|-1|=||\text{...}|||x|\underset{\text{33 db 1-es}}{\overset{}{\underbrace{-1|-1|-\text{...}|-1|}}}\mathrm{.}}\end{array}$

Itt a paraméterek a Fibonacci-számok $\{f_k\mid f_0=f_1=1$, $f_{m+1}=f_m+f_{m-1}\}$ sorozatának első hét eleme. Ismert, hogy $f_0+f_1+f_2+\text{...}+f_{m-1}=f_{m+1}-f_1=f_{m+1}-1$, ezért minden $m$-re

$\begin{array}{c}{\displaystyle f_m-\sum _{i=0}^{m-1}{f}_i=f_m-f_{m+1}+1=1-f_{m-1}\le 1.}\end{array}$

 

${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Tulassay Zsolt</span><br> Fazekas M. Főv. Gyak. Gimn.<br> 9. évf., mat. tagozat}}\hfill \end{array}}$