Kezdőlap


Cím:	Megoldásvázlatok a 2010/8. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Simon János
Füzet:	2010/december, 529 - 535. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldásvázlatok a 2010/8. sz. emelt szintű gyakorló feladataihoz

I. rész

1. Az iM bolygón az év ugyanúgy

365

napból áll, mint nálunk. A hónapok hossza szintén

28

30

vagy

31

nap. Bizonyítsuk be, hogy akkor az évnek ott is

12

hónapból kell állnia.
Mennyi a különböző hosszúságú hónapok száma ezen a bolygón, ha tudjuk, hogy ott több a

28

napos hónap, mint nálunk? (11 pont)

Megoldás. 11 hónapos nem lehet az év, mert akkor legfeljebb

11 \cdot 31 = 341

napból állna. 13 vagy több hónap esetén pedig legkevesebb

13 \cdot 28 = 364

napból állna egy év. Ekkor sem lehet 365 napos, mert ha egy 28 napos hónapot 30 naposra cserélünk, akkor már 366 napból áll egy év. Tehát 12 hónapos lehet ott is egy év. Megmutatjuk, hogy ez lehetséges is.
A 28 napos hónapok száma 3-nál több nem lehet, mert ekkor csak

3 \cdot 28 + 9 \cdot 31 = 363

napos lenne egy év. Tehát a 28 napos hónapok száma

a = 2

. Legyen

b

a 30, illetve

c

a 31 napos hónapok száma. Ekkor

30 b + 31 c = 365 - 2 \cdot 28 = 309

és

b + c = 10

.
Az egyenletrendszer megoldása:

b = 1

c = 9

, vagyis az iM bolygón 2 db 28 napos, 1 db 30 napos és 9 db 31 napos hónapból áll egy év.

2. Adjuk meg az összes olyan pozitív egész számot, melynek

90

pozitív osztója van és ezek közül legalább

10

egymást követő szám. (12 pont)

Megoldás. 10 egymást követő egész szám között biztos van egy 9-cel, egy 8-cal, egy 7-tel és egy 5-tel osztható. Tehát a keresett szám

2^{3} \cdot 3^{2} \cdot 5 \cdot 7

-tel osztható, vagyis a prímtényezős felbontása:

2^{a} \cdot 3^{b} \cdot 5^{c} \cdot 7^{d} \cdot p_{1}^{r_{1}} \cdot ... \cdot p_{n}^{r_{n}}

, ahol

a \geq 3

b \geq 2

c, d \geq 1

és

p_{i}

-k prímszámok,

r_{i}

-k pedig a megfelelő kitevők. E szám pozitív osztóinak száma:

\begin{matrix} (a + 1) (b + 1) (c + 1) (d + 1) (r_{1} + 1) \cdot ... \cdot (r_{n} + 1) . \end{matrix}

A 90-nek csak egy legalább 4 tényezős felbontása van, melyben minden tényező 1-nél nagyobb és más prímtényezője nincs, és ez az

5 \cdot 3 \cdot 3 \cdot 2

.
Ebből következik, hogy

a = 4

és

b = 2

. A 2, 3, 5, 7 prímeken kívül más prím nem szerepelhet a keresett szám prímtényezős felbontásában. Ezek alapján két lehetőség van:

2^{4} \cdot 3^{2} \cdot 5^{2} \cdot 7 = 25 200

vagy

2^{4} \cdot 3^{2} \cdot 5 \cdot 7^{2} = 35 280

.
Mindkettőnek 90 osztója van, köztük az egymást követő 1, 2,

...

, 10 is.

3. Hány megoldása van az alábbi egyenletnek, ha

x

és

y

is pozitív,

9

-nél kisebb valós szám?

\begin{matrix} log_{x} 64 + log_{8} x^{2} = - 4 sin (y + \frac{π}{3}) . \end{matrix}

(14 pont)

Megoldás. A feladat értelmezési tartománya:

0 < x < 9

x \neq 1

és

0 < y < 9

. Alakítsuk az egyenletet:

\begin{matrix} 2 log_{x} 8 + 2 log_{8} x = - 4 sin (y + \frac{π}{3}), log_{x} 8 + log_{8} x = - 2 sin (y + \frac{π}{3}) . \end{matrix}

Egy 0-tól különböző valós szám és reciprokának összege áll a bal oldalon, melynek értékkészlete ezért az

R \] - 2; 2]

.
A jobb oldal értékkészlete

[- 2; 2]

. A két oldal csak

- 2

és 2 esetén lehet egyenlő.
I. eset: Ha mindkét oldal értéke 2, akkor

x = 8

és

sin (y + \frac{π}{3}) = - 1

, azaz

\begin{matrix} y + \frac{π}{3} & = \frac{3 π}{2} + 2 k π, k \in Z \\ y & = \frac{7 π}{6} + 2 k π . \end{matrix}

Csak a

\frac{7 π}{6}

esik a megfelelő intervallumba.
II. eset: Ha mindkét oldal értéke

- 2

, akkor

x = \frac{1}{8}

és

sin (y + \frac{π}{3}) = 1

, azaz

\begin{matrix} y + \frac{π}{3} & = \frac{π}{2} + 2 k π, l \in Z \\ y & = \frac{π}{6} + 2 l π . \end{matrix}

A megfelelő intervallumba a

\frac{π}{6}

és a

\frac{13 π}{6}

esik.
Az egyenletnek a megadott feltételek mellett 3 számpár megoldása van:

\begin{matrix} (x; y) = (8; \frac{7 π}{6}); (\frac{1}{8}; \frac{π}{6}); (\frac{1}{8}; \frac{13 π}{6}) . \end{matrix}

4. Egy háromszög

a

b

c

oldalhosszai egész számok, és egyik magasságának hossza egyenlő a másik kettő összegével.
Mutassuk meg, hogy ekkor az

a^{2} + b^{2} + c^{2}

összeg négyzetszám. (14 pont)

Megoldás. Legyen

m_{c} = m_{a} + m_{b}

. A háromszög területe

t

, ekkor

2 t = a m_{a} = b m_{b} = c m_{c}

. Ezek alapján

\begin{matrix} m_{c} = \frac{2 t}{c} = m_{a} + m_{b} = \frac{2 t}{a} + \frac{2 t}{b}, amiből \frac{1}{c} = \frac{1}{a} + \frac{1}{b}, \end{matrix}

azaz

a b - (b c + a c) = 0

\begin{matrix} a^{2} + b^{2} + c^{2} = a^{2} + b^{2} + c^{2} + 2 [a b - (b c + a c)] = a^{2} + b^{2} + c^{2} + 2 a b - 2 b c - 2 a c = {(a + b - c)}^{2} . \end{matrix}

a

b

és

c

egész számok, így

a + b - c

is egész, tehát

a^{2} + b^{2} + c^{2}

valóban négyzetszám.

II. rész

5. Tizenhat pozitív valós szám összege

100

, a négyzetösszegük

1000

. Legfeljebb mekkora lehet a legnagyobb szám? (16 pont)

Megoldás. Legyen

S = a_{1} + ... + a_{15}

Q = a_{1}^{2} + ... + a_{15}^{2}

. A számtani és négyzetes közepek közötti egyenlőtlenséget felírva:

\begin{matrix} \frac{S}{15} \leq \sqrt[]{\frac{Q}{15}}, S^{2} \leq 15 Q . \end{matrix}

Tudjuk, hogy

100 - a_{16} = S

és

1000 - a_{16}^{2} = Q

{(100 - a_{16})}^{2} \leq 15 (1000 - a_{16}^{2})

16 a_{16}^{2} - 200 a_{16} - 5000 \leq 0

. Az egyenlőtlenség megoldása:

\begin{matrix} - \frac{25}{2} \leq a_{16} \leq 25. \end{matrix}

Tehát

a_{16}

legfeljebb 25 lehet (ekkor a többi 15 szám mind 5).

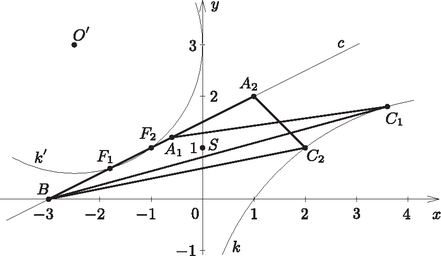
6. Adott egy háromszög

S (0; 1)

súlypontja és

c

oldalegyenesének egyenlete

x - 2 y = - 3

. A

c

oldalegyenesre illeszkedő

B

csúcs az abszcissza tengelyen van. A

C

csúcsa a

k : {(x - 5)}^{2} + {(y + 3)}^{2} = 25

egyenletű körre illeszkedik. Határozzuk meg a háromszög csúcsainak koordinátáit. (16 pont)

Megoldás. Készítsünk ábrát.

Mivel a

B

pont illeszkedik az

x

tengelyre, azért a második koordinátája 0, de

B

c : x - 2 y = - 3

egyenesre is illeszkedik, így

B (- 3; 0)

. A háromszög

C

csúcsát egy

S

középpontú

- \frac{1}{2}

arányú hasonlóság viszi az

A B

szakasz

F

felezőpontjába. Az

S

középpontú

λ = - \frac{1}{2}

arányú hasonlóság a

k

kört

k'

-be viszi. A

k

kör középpontja:

O (5; - 3)

, sugara:

r = 5

. A

k'

kör középpontja

O' (- \frac{5}{2}; 3)

, sugara

r' = \frac{5}{2}

, mert

\begin{matrix} \vec{O'} = \vec{S} + \frac{1}{2} \vec{S O} = (0; 1) + \frac{1}{2} (- 5; 4) . \end{matrix}

Ekkor

\begin{matrix} k' : {(x + \frac{5}{2})}^{2} + {(y - 3)}^{2} = \frac{25}{4} . \end{matrix}

Meghatározzuk

k'

és

c

közös pontját az

F

-et. A

c

egyenletéből kapjuk:

x = 2 y - 3

. Ezt helyettesítve

k'

egyenletébe:

\begin{matrix} {(2 y - \frac{1}{2})}^{2} + {(y - 3)}^{2} = \frac{25}{4}, 5 y^{2} - 8 y + 3 = 0. \end{matrix}

Két gyököt kapunk:

y_{1} = 0, 6

, ekkor

x_{1} = - 1, 8

; és

y_{2} = 1

, ekkor

x_{2} = - 1

.
Vagyis két

F

pont adódik:

F_{1} (- 1, 8; 0, 6)

F_{2} (- 1; 1)

. Ezekhez felhasználva, hogy

F

felezőpont és

S

harmadolópont, kiszámoljuk az

A

és a

C

koordinátáit is:

A_{1} (- 0, 6; 1, 2)

A_{2} (1; 2)

C_{1} (3, 6; 1, 8)

C_{2} (2; 1)

.
Tehát két ilyen háromszög van, ezek csúcsainak koordinátái:

\begin{matrix} \begin{matrix} A_{1} & (- 0, 6; 1, 2), & B_{1} & (- 3; 0), & C_{1} & (3, 6; 1,8), \\ A_{2} & (1; 2), & B_{2} & (- 3; 0), & C_{2} & (2; 1) . \end{matrix} \end{matrix}

7. Miből élnek a fapados légitársaságok? A Budapest‐Róma út oda és vissza 18 000 Ft. Erre a járatra egy ügynökség

35

helyet kínál. Ezeket általában az interneten való megjelenés után azonnal lefoglalják és kifizetik. Általában a foglalások kb.

20 %

-át a repülés előtt lemondják. Az egyszerűség kedvéért számoljunk pontosan

20 %

-kal. Mivel akciós áron foglaltak az ügyfelek, lemondás esetén a befizetett összeget nem kapják vissza. Ilyenkor ezeket a helyeket ,,Last Minute'' áron értékesíti a cég 15 000 Ft-ért. Ezért érdekes az ügynökség számára, hogy egy járaton mennyi lehet a lemondások számának esélye.

a)

Határozzuk meg annak a valószínűségét (a fent említett járat és ügynökség esetén), hogy a lemondások száma:
‐ pontosan

7

;
‐ legfeljebb

5

;
‐ legalább

6

b)

Számítsuk ki, hogy mennyi lehet az ügynökség várható bevétele ezen a járaton a lemondott helyek újraértékesítése után?
A lemondások újabb bevételhez juttatják az ügynökséget, ezért a tényleges

35

helyett

40

helyet hirdetnek meg a járatra. Ha véletlenül

35

-nél többen szeretnének utazni ezen a járaton (ezt hívják túlfoglalásnak), ekkor a létszám felettieknek gyorsan drágább jegyet kell vásárolnia az irodának 24 000 Ft-ért.

c)

Számítsuk ki, hogy az ügynökségnek egy járatra eredetileg eladott

40

hely esetén mennyi bevétele lesz, ha
‐

10

-en lemondják az utazást;
‐ mind a

40

-en utaznak.

d)

Mekkora a túlfoglalás valószínűsége? (16 pont)

Megoldás.

a)

Alkalmazzuk a binomiális valószínűségi eloszlást:

n = 35

p = 0, 2

\begin{matrix} p (x = 7) & = (\binom{35}{7}) \cdot 0, 2^{7} \cdot 0, 8^{28} \approx 0, 166, \\ p (x \leq 5) & = \sum_{k = 0}^{5} (\binom{35}{k}) \cdot 0, 2^{k} \cdot 0, 8^{35 - k} \approx 0, 272, \\ p (x \geq 6) & = 1 - p (x \leq 5) = 0, 728. \end{matrix}

b)

Az ügynökség

35 \cdot 18 000 = 630 000

Ft bevételhez jut. A lemondások várható értéke binomiális eloszlás esetén:

n p = 35 \cdot 0, 2 = 7

. Ezeket a jegyeket 15 000 Ft-os áron adva újabb

7 \cdot 15 000 = 105 000

Ft bevételhez jutnak.
Vagyis összesen 735 000 Ft-hoz juthat járatonként a cég.

c)

Első esetben 5 jegyet tud még ,,Last Minute'' áron eladni, így

40 \cdot 18 000 + 5 \cdot 15 000 = 795 000

Ft bevételhez jut.
Második esetben a túlfoglalás miatt 5 jegyet még vásárolnia kell, így

40 \cdot 18 000 - 5 \cdot 24 000 = 600 000

Ft bevételhez jut.

\begin{matrix} p = \sum_{k = 0}^{4} (\binom{40}{k}) \cdot 0, 2^{k} \cdot 0, 8^{40 - k} \approx 0, 07591 \approx 7, 6 % . \end{matrix}

(*)

8. Egy

12

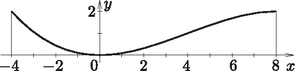
méter széles patakmeder keresztmetszetét egy adott helyen az

\begin{matrix} f : [- 4; 8] \to R, x \mapsto - \frac{1}{128} x^{3} + \frac{3}{32} x^{2} \end{matrix}

függvény grafikonja írja le.

a)

Mutassuk meg, hogy a függvénynek az origóban lokális minimumhelye, az

x = 8

-ban pedig lokális maximumhelye van.

b)

Mekkora lehet a patak legnagyobb vízállása, amikor még nem önt ki? Hány liter víz folyik át ilyenkor

1

óra alatt a teljes keresztmetszeten, ha a patakban a víz folyásának sebessége 2,5 m/s? (16 pont)

Megoldás.

a)

A deriváltak:

f' (x) = - \frac{3}{128} x^{2} + \frac{3}{16} x

f'' (x) = - \frac{3}{64} x + \frac{3}{16}

\begin{matrix} f' (x) = \frac{3 x (8 - x)}{128} = 0. \end{matrix}

Az első derivált zérushelyei: 0 és 8
A második derivált 0-nál felvett értéke pozitív:

\frac{3}{16}

, tehát itt a függvény konvex, azaz

x = 0

-ban lokális minimumhelye van.
A második derivált 8-nál felvett értéke negatív:

- \frac{3}{16}

, tehát a függvény itt konkáv, azaz

x = 8

-ban lokális maximumhelye van.

b)

f (x)

folytonos a

[- 4; 8]

-on.
Ha

- 4 < x < 0

, szigorúan monoton csökken, mert

f' (x)

negatív.
Ha

0 < x < 8

, szigorúan monoton nő, mert

f' (x)

pozitív.
Mivel

f (- 4) = 2

és

f (8) = 2

, azért a patak legmagasabb vízállása 2 méter lehet.

\begin{matrix} \int_{- 4}^{8} (2 - f (x)) d x = \int_{- 4}^{8} (2 + \frac{1}{128} x^{3} - \frac{3}{32} x^{2}) d x = {[2 x + \frac{1}{512} x^{4} - \frac{1}{32} x^{3}]}_{- 4}^{8} = 13, 5. \end{matrix}

A mederkeresztmetszet területe 13,5 m

^{2}

. 1 óra alatt a víz

3600 \cdot 2, 5 = 9000

méter utat tesz meg. Tehát az átfolyó vízmennyiség

9000 \cdot 13, 5 = 121 500

.
Vagyis ez 121 500 m

^{3}

, azaz 121 500 000 liter vizet jelent óránként.

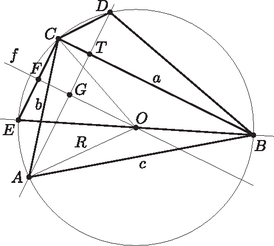
9. Egy hegyesszögű háromszög oldalainak hossza:

a = 20

b = 13

és

c = 21

. A köré írható kör középpontja

O

. Az

A

csúcsból induló magasságvonalnak a köré írt körrel vett

A

-tól különböző metszéspontja

D

. A

B O

egyenes köré írt körrel vett

B

-től különböző metszéspontja

E

. Határozzuk meg a

B E C D

négyszög területét. (16 pont)

Megoldás. A

B E C D

négyszöget

B C

átlója két háromszögre bontja. Ezek területének összegével határozzuk meg a négyszög területét.

A háromszög területe (

R

a körülírt kör sugara):

\begin{matrix} t & = \frac{a m}{2} = \frac{a b c}{4 R}, \\ t & = \sqrt[]{s (s - a) (s - b) (s - c)} = \\ = \sqrt[]{27 \cdot 7 \cdot 14 \cdot 6} = 126, \end{matrix}

ami alapján

m = \frac{63}{5}

, valamint

R = \frac{a b c}{4 t} = \frac{65}{6}

.
A Pitagorasz-tételt alkalmazva a

B E C

derékszögű háromszögre:

\begin{matrix} E C = \sqrt[]{{(\frac{65}{3})}^{2} - 20^{2}} = \sqrt[]{\frac{65^{2} - 20^{2} \cdot 3^{2}}{3^{2}}} = \frac{25}{3} . \end{matrix}

B E C

háromszög területe:

\begin{matrix} \frac{20 \cdot \frac{25}{3}}{2} = \frac{250}{3} . \end{matrix}

Húzzunk párhuzamost az

O

ponton keresztül a

B C

szakasszal, ez legyen

f

. Mivel

E C ⊥ B C

, azért

f ⊥ E C

E O C

háromszög egyenlőszárú (

E O = C O = R

), tehát

f

E C

felezőmerőlegese. Ugyanezért

f

A D

-nak is felezőmerőlegese. Az

f

egyenes az

E C

-t

F

-ben,

A D

-t

G

-ben metszi. A magasság talppontja:

T

.
Az

F C T G

négyszög téglalap:

F C = G T = \frac{25}{6}

\begin{matrix} m - \frac{25}{6} & = A G = G D = T D + \frac{25}{6}, \\ m - \frac{25}{3} & = T D = \frac{63}{5} - \frac{25}{3} = \frac{64}{15} . \end{matrix}

B C D

háromszög területe:

\begin{matrix} \frac{20 \cdot \frac{64}{15}}{2} = \frac{128}{3} . \end{matrix}

B E C D

négyszög területe egyenlő a

B E C

és a

B C D

háromszögek területének összegével:

\begin{matrix} T_{B E C D} = \frac{250}{3} + \frac{128}{3} = \frac{378}{3} = 126. \end{matrix}

Megjegyzés: 1. Az

A B C

háromszög és

B E C D

négyszög területe egyenlő.
2. A feladat megoldható a koszinusz-, a Pitagorasz-tétel, és a szinuszos területképlet felhasználásával is.