Cím: Matematika és fizika TOTÓ megoldása (a 2014. évi Őszi KöMaL Ankéton)
Füzet: 2015/január, 39 - 43. oldal  PDF  |  MathML 
Hivatkozás(ok):2015/január: Matematika és fizika TOTÓ (a 2014. évi Őszi KöMaL Ankéton)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1
A telitalálatos szelvény:

1,2,X,X,2,X,2,X,1,2,2,X,2,2.

A legtöbb (13) találatot Fehér Zsombor (Budapesti Fazekas M. Ált. Isk. és Gimn., 12. évf.) és Sal Kristóf (Budapesti Fazekas M. Ált. Isk. és Gimn., 10. évf.) érte el.
Az alábbiakban rövid útmutatást adunk a feladatok megoldásához.
 
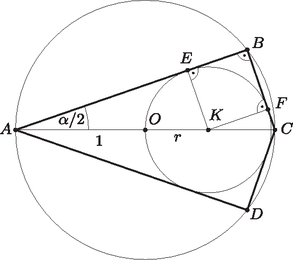
1. ABCD deltoidunk húrnégyszög, ezért az AC szimmetriatengelye a körülírt körben átmérő, továbbá a B csúcsnál levő szöge derékszög. Legyen még a körülírt kör középpontja O, a beírt köré ‐ szintén a tengelyen ‐ K, és legyen KC<KA, sugaraik 1, illetve r, végül a beírt kör érintési pontja az AB oldalon E, a BC-n F.

 
 

A KE és a KF sugár párhuzamos a BC, illetve a BA oldallal, ezért AKE és KCF hasonló derékszögű háromszögek:
AE:KE=KF:CF,AE⋅CF=KE⋅KF=r2.
Az átfogók pedig 1+r, illetve 1-r, mert O rajta van a beírt körön és K az OC sugáron, így
AE⋅CF=(1+r)2-r2⋅(1-r)2-r2=(1+2r)(1-2r).
Ezeket egybevetve r2-re másodfokú egyenletet kapunk, és abból
1-4r2=r4,r=5-2≈0,4859,
(r2 másik értéke negatív).
Most már a deltoid A csúcsánál levő α szögre
sinα2=r1+r,α≈38,17∘,
a C-nél levő szög ennek kiegészítő szöge, vagyis ennél nagyobb.
 
2. A rugókat egyforma nagyságú erő feszíti, és ha ez nem 3 N lenne, akkor a középső rugó végpontjai nem lennének egyensúlyban.
 
3. Jelöljük T-vel a keresett telefonszámot. T  3-mal osztva 0, 1 vagy 2 maradékot adhat. Tudjuk azt is, hogy T páratlan, tehát 4-gyel osztva páratlan maradékot ad. Eszerint a szóban forgó közös maradék 1.
A feltételből következik, hogy T-1 osztható 3-mal, 4-gyel, 7-tel, 9-cel, 11-gyel és 13-mal. Egyelőre csak annyit használunk föl, hogy T-1 osztható 7⋅11⋅13=1001-gyel: 1001 hatjegyű többszörösei ABCABC alakúak. Mivel T páratlan, nem végződik 0-ra, és így T-1 és T csak az utolsó számjegyükben különböznek. Így A=7, B=2, tehát
T-1=72C72C.

A 9-cel való oszthatóság miatt T-1 jegyeinek összege is osztható 9-cel. Mivel
7+2+C+7+2+C=18+2C,
így 2C is 9 többszöröse. Ez csak a C=0 vagy a C=9 esetben lehetséges, de T-1 utolsó jegye páros. Ha C=0, akkor valamennyi feltétel teljesül, azaz T=720721.
 
4. A tömegközéppont mindkét esetben
x=ℓ4ϱ2-ϱ1ϱ2+ϱ1
távolságra lesz az ℓ hosszú, ϱ1 és ϱ2 sűrűségű részekből álló pálca középpontjától.
 
5. Az alábbi egyenletrendszert kell megoldanunk, ahol x a 10, y a 20, z az 50, végül t a 100 forintos érmék számát jelöli:
x+y+z+t=5,(1)10x+20y+50z+100t=170.(2)

A második egyenlet tizedrészéből kivonva az elsőt, kapjuk az eredetivel ekvivalens
x+y+z+t=5,(1)y+4z+9t=12(3)
egyenletrendszert.
A megoldások nem negatívak, így (3) alapján t≤1. Két esetet különböztetünk meg, aszerint, hogy t=1 vagy t=0.
a) Ha t=1, akkor egyenletrendszerünk így alakul:
x+y+z=4,(1a)y+4z=3.(3a)

(3a) alapján z<1, így z=0, és y=3, végül (1a) szerint x=1.
b) Ha t=0, akkor egyenletrendszerünk:
x+y+z=5,(1b)y+4z=12.(3b)

(3b) alapján y=12-4z, emiatt y osztható 4-gyel. Mivel (1b) szerint y≤5, így y=4, vagy y=0. Ha y=4, akkor z=2, de (1b)-ből y+z≤5, tehát így nem kapunk gyököt.
Ha y=0, akkor z=3, így (1b)-ből x=2.
Minden lehetőséget végignéztünk, így az egyenletrendszernek két megoldása van. Ezek:
x1=1;y1=3;z1=0;t1=1,x2=2;y2=0;z2=3;t2=0.

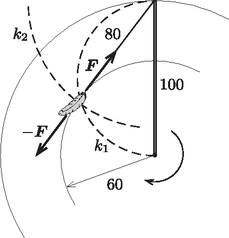
6. Ha a tollpihe valamilyen állandósult pályán mozog, akkor ez csak kör lehet, hiszen ilyenkor a tollpihe az ostornyéllel együttforgó koordináta-rendszerből szemlélve áll. A tollpihe elhanyagolhatóan kicsi tömege miatt a Newton-egyenletben a nehézségi erő és ma helyébe nullát írhatunk. A mozgásegyenlet tehát erre az állításra egyszerűsödik: a cérnaszálban ható erő és a közegellenállási erő eredője nulla.

 
 

A cérnaszál egyenese a tollpihe pályakörének érintője. A pályakör sugarát az ábrán látható (R=100 cm átmérőjű) k1 Thalész-kör és az ostornyél mozgásban levő vége körüli L=80 cm sugarú k2 kör metszéspontja adja meg; nagysága:
r=R2-L2=60cm.  
(Ha a cérna hosszabb lenne, mint a pálca, akkor a tollpihének nem alakulhatna ki stabil, állandósult pályája.)
 
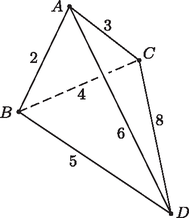
7. Próbáljunk meg tetraédert építeni az adott élekből. Nem szerepelhetnek ugyanabban a háromszögben a 2 cm-es és a 8 cm-es élek, hiszen a 2 cm-es élt a többi négy közül még a legnagyobb, a 6 cm-es él sem egészíti ki 8 cm-nél hosszabbra, márpedig egy háromszögben két oldal összege nagyobb a harmadiknál. Jelöljük a 2 cm-es él végpontjait A-val, B-vel, a 8 cm-eséit C-vel, D-vel, tudjuk már, hogy ezek különbözőek.

 
 

A többi 4 él mindegyikének az egyik végpontja az A, B, a másik a C, D pontok közül való. Válasszuk úgy a betűzést, hogy a 3 cm-es él két végpontja A és C legyen. Az ABC háromszög harmadik oldala, BC most már csak a 4 cm-es él lehet, hiszen a másik kettő mellett az AB+AC=5 cm-es összeg túl kicsi lenne. Ugyancsak kevés az 5 cm-es él az ACD háromszög harmadik oldalának, így AD=6, BD=5. Ezek mellett az ABD háromszögben AD=6 cm, AB+BD=7 cm, a BCD háromszögben CD=8 cm, BC+BD=9 cm, tehát a keresett tetraéder valóban létrejön.
Tegyük fel most, hogy az adott elemekből ketten is felépítették a keresett tetraédert. Betűzzük az első tetraéder csúcsait a fenti meggondolás szerint A-val, B-vel, C-vel, D-vel, a másodikét A'-vel, B'-vel, C'-vel, D'-vel, ekkor tehát
AB=A'B',AC=A'C',BC=B'C',AD=A'D',BD=B'D',CD=C'D'.(1)
A második A'B'C' lapja egybevágó az első ABC lapjával, tehát ráhelyezhető úgy, hogy A' az A-ra, B' a B-re, C' a C-re kerüljön. Ezután a D' pont rendre ugyanolyan messze lesz az A, B, C pontoktól, mint a D. Ha D és D' azonosak, készen vagyunk, ha nem, tekintsük a DD' szakaszt. Az A, B, C pontok mindegyike egyenlő távolságra van ennek a végpontjaitól, tehát ezek a pontok benne vannak a szakasz felezőpontján átmenő, a szakaszra merőleges S síkban. Így ha az ABCD tetraédert S-re tükrözzük, az átmegy az ABCD' tetraéderbe. A két tetraéder tehát mindig egybevágó.
 
8. A lencsén átjutó fénysugarak a síktükrön visszaverődve mégegyszer áthaladnak a lencsén, éppen úgy, mintha két 6 dioptriás lencse lenne egymás mellett. Ezek dioptriaszáma összeadódik, tehát 12 lesz.
 
9. Tegyük föl, hogy a lift úgy mozgott, hogy maximális utat tett meg. Ekkor minden megállás után irányt változtatott. Ha ugyanis az i-edik, j-edik szintekre egymás után, irányváltoztatás nélkül érkezett volna, akkor az i-edik szinten való megállást kihagyva, majd az út befejezése után ide visszatérve, az így módosított út hosszabb, mint a lift által megtett út, amiről pedig feltettük, hogy maximális.
Jelölje mi az i-edik megállás szintjét, i=1,2,...,10. A lift által megtett út
m1+(m1-m2)+(m3-m2)+(m3-m4)+...+(m9-m10)==2[(m1+m3+m5+m7+m9)-(m2+m4+...+m8)]-m10.


Látható, hogy a megtett út akkor maximális, ha a fenti összegben a 10, 9, 8, 7, 6 szintek pozitív, a megmaradó szintek negatív előjellel szerepelnek. Mivel a kivonandók közül m10 együtthatója a legkisebb, ezért m10=5, vagyis a lift végül az 5-dik szinten állt meg. A további mi értékek ‐ a fenti megszorítás mellett ‐ tetszőlegesek lehetnek. A fenti megszorításnak eleget tevő mi értékekhez tartozó maximális úthossz 220 m.
 
Megjegyzések. 1. A megoldásból nyilvánvaló, hogy a lift nemcsak egyetlen módon teheti meg a maximális 220 m-t. Az ilyen utak száma 5!⋅4!=2880.
2. A feladat könnyen általánosítható n emeletes házra. Ekkor a lift maximálisan 2n(n+1) méternyi utat tesz meg.
 
10. A rugalmas ütközések és a ferde hajítások összefüggéseinek felírása után ‐ elég hosszú számolással ‐ belátható, hogy a parabolák fókuszpontjai az ejtési ponton átmenő, 2α meredekségű egyenesen helyezkednek el. Célszerű a labda mozgását a lejtővel párhuzamos és arra merőleges tengelyekkel rendelkező koordinátarendszerben tárgyalni. A lejtőre merőleges irányban a labda úgy mozog, mintha a nehézségi gyorsulás gcosα lenne; a felpattanások magassága és az ütközések közötti idő pedig minden ütközés után ugyanakkora. A lejtővel párhuzamos irányban a labda egyenletesen gyorsulva mozog, gyorsulása gsinα.
 
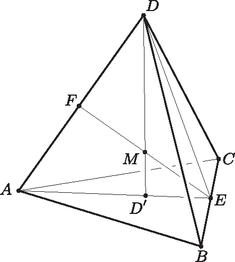
11. Jelöljük a tetraéder csúcsait A, B, C és D-vel. Mivel a tetraéder szabályos, bármely magasságvonala a szemközti szabályos háromszöget a körülírt körének középpontjában metszi. A magasságvonal körül 120∘-kal elforgatva a tetraédert, önmagába megy át. Ez a forgatás a tetraéder köré, a tetraéderbe írt gömböt, valamint az élérintő gömböt is önmagába viszi át, emiatt mindhárom gömbnek a középpontja a tetraéder magasságpontja, M.

 
 

Jelöljük a D csúcsnak az ABC síkra való merőleges vetületét D'-vel. A DD' magasságvonal tartalmazza a tetraéder M magasságpontját és MD' a tetraéderbe írható gömb sugarával egyenlő. Érintse az élérintő gömb az AD élt F-ben, a BC élt E-ben. Így MF⊥AD és ME⊥BC, továbbá ME=MF és nyilván F felezi AD-t, E felezi BC-t, hiszen MD=MA=MC=MB a tetraéder köré írt gömb sugarával egyenlő. A DEA háromszög egyenlő szárú (ED=EA) és MF merőlegesen felezi AD-t, így át kell, hogy menjen a szemközti csúcson, E-n, azaz E, M és F egy egyenesbe esik. Ebből következik, hogy EMD' és DMF háromszögek M csúcsnál levő szögei csúcsszögek, tehát egyenlők, s mivel MD'E és MFD szögük derékszög, így hasonlóak és megfelelő oldalaikra:
EMMD'=DMMF,ME=MFmiattEM2=MD'⋅DM.

 
12. Ha a telített vízgőz térfogatát lassan csökkentjük, a hőmérséklete állandó marad, a nyomása sem tud megváltozni, mert az csak a hőmérséklettől függ, így a gáztörvény szerint a részecskeszámnak kell csökkennie. A lassan összenyomott gőz egy része tehát kicsapódik.
Ha a térfogatot olyan hirtelen növeljük meg, hogy nincs idő számottevő hőcserére a vízgőzt tartalmazó tartály és a környezete között, akkor a hőmérséklet lecsökken (adiabatikus tágulás). Az új, alacsonyabb hőmérséklethez tartozó telítési gőznyomás kisebb lesz, mint az eredeti, sőt, annak ellenére, hogy a térfogat nő, a gőz egy része kicsapódik.
A gőz kicsapódása tehát a térfogat csökkentésével és növelésével egyaránt előidézhető, a térfogatváltozás tényleges hatása a folyamat sebességétől függ.
 
13. Az ábrán 1-től 25-ig megszámoztuk az 5×5-ös tábla mezőit.
 
12091431015219242182541316116231872217125
 

Könnyen ellenőrizhető, hogy ha egy ló az 1. számú mezőről kiindulva mindig a soron következő számú mezőre lép, akkor 24 lépésben minden mezőt érint. Így ha 13-nál több lovat állítunk fel az 5×5-ös táblára, akkor ezek közt feltétlenül lesz legalább kettő, amelyek szomszédos sorszámú mezőkre kerülnek, tehát a számozás tulajdonsága miatt ütik egymást. Az 5×5-ös táblán tehát 13 ló elhelyezhető a kívánt módon (minden páratlanadik mezőn egy), annál több már nem.
 
13+1. Egy általános érvényű tétel szerint ha egy (F1) zárt felület sehol nem ,,lóg ki'' egy másik (F2) felület által határolt térrészből, akkor a nekik megfelelő alakú fémtestek kapacitására fennáll: C1<C2. (A tétel bizonyításához a feltöltött kondenzátor elektrosztatikus energiáját érdemes vizsgálni, miközben a kisebb felületet apró lépésekben a másiknak megfelelő alakúra ,,kalapáljuk''.)
A fémkocka éppen ,,belefér'' a megadott méretű fémgömbbe, emiatt a kocka kapacitása biztosan kisebb, mint a fémgömbé.
1A kérdések a 26. oldalon találhatók.