Kezdőlap


Cím:	Beszámoló a 2014. évi Eötvös-versenyről
Szerző(k):	Tichy Géza , Vankó Péter , Vigh Máté
Füzet:	2014/december, 553 - 560. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 2014. évi Eötvös-versenye október 17-én délután 3 órai kezdettel tizenöt magyarországi helyszínen¹ került megrendezésre. A versenyen a három feladat megoldására 300 perc áll rendelkezésre, bármely írott vagy nyomtatott segédeszköz használható, de zsebszámológépen kívül minden elektronikus eszköz használata tilos. Az Eötvös-versenyen azok vehetnek részt, akik vagy középiskolai tanulók, vagy a verseny évében fejezték be középiskolai tanulmányaikat. Összesen 93 versenyző adott be dolgozatot, 18 egyetemista és 75 középiskolás.
Ismertetjük a feladatokat és azok megoldását.

*

1. feladat. Egy

M

tömegű,

L

hosszúságú, hajlékony futószőnyeget szorosan felgöngyöltünk egy

R

sugarú hengerré. Ha a felgöngyölt szőnyeget elengedjük, az magától kitekeredik. (A gördülési ellenállás elhanyagolható.)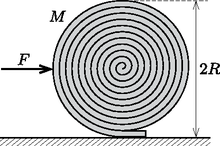

1. ábra

a)

Milyen erőhatással magyarázható a jelenség?

b)

Mekkora vízszintes erővel akadályozható meg a szőnyeg kitekeredése?

Megoldás.

a)

A guriga tömegközéppontja nem esik az alátámasztási pont fölé, az így fellépő forgatónyomaték görgeti ki a szőnyeget.

b)

A guriga egyensúlyát biztosító vízszintes

F

erőt a virtuális munka elvéből határozhatjuk meg. Ha a nem teljesen felgöngyölt gurigát kicsiny

Δ x

távolsággal feljebb görgetjük, az

F (x)

erő által végzett munka a szőnyeg helyzeti energiájának (kicsiny) megváltozását biztosítja:

\begin{matrix} F (x) Δ x = Δ E_{h} . \end{matrix}

A szőnyeg helyzeti energiája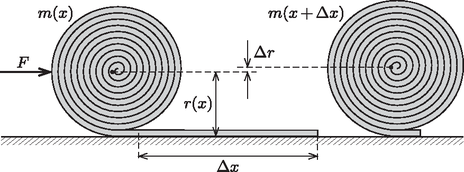

\begin{matrix} E_{h} (x) = m (x) g r (x), \end{matrix}

amely a feltekeredés közben két okból is növekszik: egyrészt magasabbra kerül a tömegközéppontja, másrészt feltekerés közben a szőnyeg ,,hízik'' is. (A földön fekvő rész helyzeti energiája 0, azzal nem kell számolnunk.)

2. ábra

A helyzeti energia kicsiny megváltozása eszerint

\begin{matrix} Δ E_{h} = m g \cdot Δ r + Δ m \cdot g r . \end{matrix}

A szőnyeg

x

hosszúságú darabjának feltekerésekor kialakuló szőnyegguriga

m

tömege egyenesen arányos a felgöngyölt rész hosszával, így

\begin{matrix} Δ m = \frac{m}{x} Δ x és m = \frac{M}{L} x, \end{matrix}

hiszen

x = L

esetén a tömeg éppen

M

. A guriga keresztmetszetének területe is arányos

x

-szel, vagyis a guriga sugarára fennáll:

\begin{matrix} r^{2} = \frac{R^{2}}{L} x . \end{matrix}

Ebből kifejezhetjük

Δ r

-t is

Δ x

segítségével (felhasználva, hogy

Δ r

kicsi):

\begin{matrix} \frac{R^{2}}{L} Δ x & = {(r + Δ r)}^{2} - r^{2} \approx 2 r Δ r, \\ Δ r & = \frac{1}{2} \frac{r}{x} Δ x . \end{matrix}

Mindezt behelyettesítve

Δ E_{h}

kifejezésébe:

\begin{matrix} Δ E_{h} = \frac{3}{2} \frac{m g r}{x} Δ x . \end{matrix}

Ebből pedig az

x

darabon feltekert guriga megtartásához szükséges erő:

\begin{matrix} F (x) = \frac{3}{2} \frac{m g r}{x} = \frac{3}{2} \frac{M g R}{L} \sqrt[]{\frac{x}{L}}, \end{matrix}

amelyből a keresett

F

erő

x = L

helyettesítéssel

\begin{matrix} F = \frac{3}{2} \frac{R}{L} M g . \end{matrix}

Megjegyzések. 1. Néhány versenyző próbálkozott a virtuális munka elvével, de a helyzeti energia megváltozásában elfelejtkeztek az egyik tagról. A fenti megoldásban az erőt a feladat kérdésénél kicsit általánosabban,

x

függvényében egy tetszőleges helyzetben is megadtuk, ez lehetőséget ad a megoldás ellenőrzésére. Az erő elmozdulás szerinti integrálásával meghatározzuk a feltekeréshez szükséges teljes munkát:

\begin{matrix} \int_{0}^{L} F (x) d x = \int_{0}^{L} \frac{3}{2} \frac{M g R}{L} \sqrt[]{\frac{x}{L}} d x = M g R, \end{matrix}

ez valóban megegyezik a teljesen feltekert szőnyeg helyzeti energiájával.
2. A versenyzők többsége statikai megoldással próbálkozott. A feladat így is megoldható, azonban még könnyebb tévedni. A statikai megoldásban a forgatónyomatékok egyensúlyát írjuk fel a szőnyeg alátámasztási pontjára:

\begin{matrix} F R = M g x_{tkp}, \end{matrix}

ahol

x_{tkp}

a guriga tömegközéppontjának távolsága az alátámasztáson át húzott függőleges egyenestől. A feladat ennek meghatározása.
A tömegközéppont két okból sem esik az alátámasztási pont fölé: egyrészt a guriga spirális alakja miatt a guriga érintője nem merőleges a spirál középpontjából az érintési ponthoz húzott sugárra, másrészt a guriga tömegközéppontja nem a spirál középpontjába esik. (Mindkét okra rájöttek versenyzők, de senki se gondolt mindkettőre, így helyes megoldás nem született.)
A guriga ,,ferdesége'', és így a spirál középpontjának helye könnyen meghatározható a menetemelkedésből. A tömegközéppont ebből származó elmozdulása

\begin{matrix} x_{1} = \frac{1}{2} \frac{R^{2}}{L} . \end{matrix}

A guriga tömegközéppontjának a spirál középpontjához viszonyított helyét sokféleképp meg lehet határozni, erre sok helyes megoldás érkezett az integrálástól az ügyes trükkökig. Egy lehetőség például az, hogy a gurigát gondolatban kiegészítjük egy további fél menettel, melynek tömegét és tömegközéppontjának helyét is ismerjük: ekkor a szimmetria (és a szőnyeg kis vastagsága) miatt a tömegközéppont ugyanolyan távolra kerül a spirál középpontjától, csak éppen a másik irányba ‐ és ebből a keresett távolság már könnyen kiszámolható:

\begin{matrix} x_{2} = \frac{R^{2}}{L} . \end{matrix}

A két részeredményt összeadva

\begin{matrix} x_{tkp} = x_{1} + x_{2} = \frac{3}{2} \frac{R^{2}}{L}, \end{matrix}

amiből a keresett erőre valóban helyes eredményt kapunk.
3. Néhány versenyző a szőnyeg rugalmas tulajdonságaival próbálta magyarázni a jelenséget. A feladat szövegében viszont az áll, hogy a szőnyeg hajlékony, ami arra utal, hogy ezt a hatást nem kell figyelembe venni. (Nem is voltak megadva olyan adatok, amikre ez esetben szükség lenne.)

2. feladat. András, Bence és Csaba egyhetes biciklitúrán vesznek részt. A reggelihez minden nap teát isznak; a teavizet a saját fémbögréjükben forralják fel egy (nyomáscsökkentő szelep nélküli) butántöltésű gázpalack lángja fölött. A túra végéhez közeledve érdekes megfigyelést tesznek: a teavíz felforralásához feltűnően több időre van szükség, mint a túra elején.
András szerint ebben nincs semmi különös: ahogy csökken a palackban a gáz mennyisége, úgy csökken a nyomás, így a gázláng is gyengébben ég. Bence figyelmeztet rá, hogy a palackban folyadék is van, ezért a gáz nyomása a mennyiségtől függetlenül mindig a telítési gőznyomással egyenlő. Szerinte azért csökkent le a nyomás, mert a folyadék már teljesen elfogyott a palackból. Csaba ekkor meglötyögteti a palackot, és meglepve tapasztalja, hogy még van benne valamennyi folyadék.
Mi lehet az oka a forralási idő meghosszabbodásának?

Megoldás. A gázpalack használata közben a palackból gáz áramlik ki, a kiáramló gázt a palackon belül a folyékony bután forrása pótolja. A folyadék elforralásához energiára van szükség, amelyet ‐ legalább részben ‐ a folyékony butánból von el, és így a bután lehűl. Amikor a palackban már csak kevés bután van, akkor sokkal kisebb a hőkapacitása, mint a teli palacknak, és így jobban lehűl. A folyadék-gáz rendszerekben kialakuló egyensúlyi gőznyomás viszont erősen hőmérsékletfüggő, a hőmérséklet aránylag csekély csökkenése is a nyomás jelentős csökkenését, és ezzel a vízforralási idő jelentős meghosszabbodását okozza.

Megjegyzések. 1. A forralási idő meghosszabbodását természetesen nagyon sok más tényező is okozhatja: a levegő vagy a víz hőmérsékletének csökkenése, a légnyomás növekedése (az időjárás vagy a tengerszint feletti magasság változása miatt), a főző szelepének eldugulása, és így tovább. (A feladatban azonban ezekről nincsen szó, és a fiúk ‐ akik láthatóan elég okosak ‐ szintén nem beszélnek róla.) Általában igaz, hogy egy jelenséget végtelen sok hatás befolyásol kisebb-nagyobb mértékben. Így fel se sorolhatjuk azt a végtelen sok hatást, amit elhanyagolunk, nem veszünk figyelembe. A feladat annak a néhány effektusnak a felismerése és leírása, amelyek a jelenséget alapvetően meghatározzák.
Erre a feladatra hat versenyző adott hibátlan megoldást. Még többen rájöttek arra, hogy a palack lehűl, de nem elemezték a folyadék mennyisége és a lehűlés mértéke, illetve a lehűlés és az egyensúlyi gőznyomás csökkenése közti kapcsolatot.
2. A gyakorlatban használt gázpalackok jelentős részében nem tiszta bután, hanem propán-bután keverék található. A folyadékkeverékek gőznyomását a Raoult-törvény írja le. Ilyenkor a két komponens nem egyforma sebességgel fogy a palackból, és ez is okozhatja a nyomás csökkenését. A feladatban ezért szerepel tiszta bután töltésű palack. Ilyen is kapható: főleg nyáron előnyös, mert a bután gőznyomása jóval kisebb, mint a propáné, így nagy melegben se alakul ki túl nagy nyomás.
3. Az eredményhirdetés végén a jelenséget kísérlettel is demonstráltuk: egy már majdnem kiürült palack aljára platina ellenállás-hőmérőt ragasztottunk, melynek ellenállását egy multiméterrel mértük. A palack szelepének megnyitása után az ellenállás látványosan csökkent, ami a hőmérséklet csökkenését igazolta.

3. feladat. Egy

R

sugarú, rézből készült, vékony falú gömbhéjat szigetelő állványra helyezünk. A gömb egyik pontjába hosszú, sugárirányú, egyenes vezetővel

I

erősségű áramot vezetünk, rá merőlegesen (szintén sugárirányban) pedig elvezetjük azt.

3. ábra

Milyen mágneses mező alakul ki a gömb belsejében, illetve a gömbön kívül? Mekkora például a mágneses indukcióvektor az áramok be- és kivezetési pontja között ,,félúton'' lévő

P

pontban, egy ,,hajszálnyival'' a gömb felületén kívül?

Megoldás. Számítsuk ki először egyetlen félegyenes mentén befolyó, majd a gömb felületéről radiálisan, gömbszimmetrikusan távozó áram által létrehozott mágneses teret! (Ez az árameloszlás ténylegesen megvalósítható, ha az igen jól vezető gömböt valamekkora vezetőképességű ,,végtelen'' közegbe helyezzük, és feszültséget kapcsolunk rá.)
Egyetlen áramvezető esetén a mágneses mező az egyenes vezető által kijelölt ,,tengely'' körül forgásszimmetrikus, és az indukcióvonalak, ahogy ezt meg fogjuk mutatni, kör alakúak.
A mágneses indukció nagyságát az Ampre-féle gerjesztési törvényből határozhatjuk meg. A gömb belsejében képzeletben felvett zárt görbe nem ölel körül áramot, ezért itt (amikor

r < R

) nincs mágneses tér. A gömbön kívül (

r > R

) viszont a gerjesztési törvény így írható (lásd a 4. ábrát):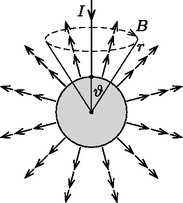

\begin{matrix} 2 π r sin ϑ \cdot B (r, ϑ) = μ_{0} (I - \frac{1 - cos ϑ}{2} I) . \end{matrix}

4. ábra

Felhasználtuk, hogy a 4. ábrán szaggatottan jelölt körvonallal határolt

r

sugarú gömbsüveg felszíne

2 π r^{2} (1 - cos ϑ)

, az

r

sugarú gömb felszíne pedig

4 π r^{2}

, emiatt a gömbszimmetrikusan kifolyó áram számításba vehető része

I (1 - cos ϑ) / 2

erősségű. A mágneses indukció nagysága tehát

\begin{matrix} B (r, ϑ) = \frac{μ_{0} I}{4 π} \frac{1 + cos ϑ}{r sin ϑ} = \frac{μ_{0} I}{4 π} \cdot \frac{ctg (ϑ / 2)}{r} . \end{matrix}

Az áramvezető közelében (

ϑ \approx 0

) a kis szögekre érvényes

ctg (ϑ / 2) \approx 2 / ϑ

összefüggés miatt éppen a végtelen egyenes vezető körüli mágneses mezőt kapjuk vissza; a bevezetett árammal ellentétes oldalon pedig (

ϑ \to 180^{\circ}

) az indukció fokozatosan eltűnik.
Végezzük el ugyanezt a számítást a

90^{\circ}

-kal elforgatott egyenes vezetőn kivezetett és gömbszimmetrikusan bevezetett áramokra is, majd szuperponáljuk a két elrendezés mágneses terét (5. ábra). A gömb belsejében továbbra is mindenhol nulla lesz az indukció, a kérdéses

P

pontban pedig (a gömbön kívül)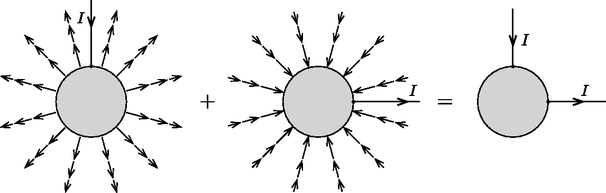

\begin{matrix} B_{P} = 2 \cdot B (R, 45^{\circ}) = \frac{μ_{0} I}{2 π R} ctg 22, 5^{\circ} = \frac{μ_{0} I}{2 π R} (\sqrt[]{2} + 1) . \end{matrix}

5. ábra

Hátra van még annak igazolása, hogy a 4. ábrán látható tengelyszimmetrikus elrendezésben mágneses indukcióvonalak csak kör alakúak lehetnek (bár ezt a bizonyítást a versenyzőktől nem vártuk el). A tengelyszimmetria nem zárná ki, hogy az indukciónak ,,radiális'' és a szimmetriatengellyel párhuzamos, ,,hosszanti'' komponensei is legyenek. (Gondoljunk például a köráram szintén tengelyszimmetrikus terére!)
Illesszünk az egyenes vezetőre és egy rajta kívül lévő

P

pontra egy síkot, majd tükrözzük az egész elrendezést erre a síkra! A tükrözés után az árameloszlás pontosan olyan marad, amilyen eredetileg volt, tehát a tükrözés során a mágneses mező sem változhat meg.
A mágneses indukció ‐ jóllehet vektorként szoktuk ábrázolni ‐ nem egy irányított szakasz, a tér egyik pontjából egy másikba mutató nyíl (ún. polárvektor, mint amilyen a helyvektor vagy az elektromos térerősség), hanem egy irányított körvonallal és egy nagysággal megadható mennyiség (mint pl. a szögsebesség vagy a forgatónyomaték). Az ilyen mennyiségeket axiálvektornak nevezik. A mágneses indukció körvonalát úgy kaphatjuk meg, ha megadjuk azt a síkot és körüljárási irányt, amely mentén egy megfelelő sebességgel mozgó töltött részecske (az adott pont közelében) körmozgást végezhet. A sík normálisa és a körmozgás körüljárási iránya biztosítja egyértelműen az indukcióvektor irányítottságát.
Belátjuk, hogy a feladatban szereplő mágneses mezőnek nem lehet ,,radiális'' (vagyis az áramvezetőtől a

P

pontba mutató vektorra merőleges síkú körvonallal szemléltethető) komponense. Ez a komponens ugyanis az említett tükrözés során előjelet váltana, de ugyanakkor változatlannak is kell maradnia, ez a két feltétel pedig csak úgy teljesülhet egyszerre, ha a vizsgált indukciókomponens nagysága zérus (6. ábra

a)

része). Ugyanilyen okok miatt a mágneses indukciónak nem lehet ,,hosszanti'' (az egyenes vezetőre merőleges síkú körvonallal megadható) komponense sem, hiszen az is előjelet váltana a tükrözés során, pedig értékének változatlannak kell maradnia (6. ábra

b)

része). A mágneses indukció harmadik, a tükrözés síkjába eső körvonallal megadható komponenséről semmit nem állíthatunk, hiszen azt a tükrözés művelete változatlanul hagyja (6. ábra

c)

része).

6. ábra

Megjegyzés. A feladatra két teljesen hibátlan megoldás érkezett. Az egyik versenyző bebizonyította, hogy a gömb felületén az áramvonalak körívek, és meghatározta az árameloszlást, majd ebből a keresett mágneses indukciót. A másik versenyző azt mutatta meg, hogy a gömbön kívül az elrendezésnek ugyanolyan mágneses tere van, mint egy két félegyenesből összerakott L alakú vezetéknek (amely viszont a Biot‐Savart-törvénnyel könnyen meghatározható). Erre két további versenyző is ,,ráérzett'' (és így helyes eredményt kapott), de ezt nem igazolta.

*

Az ünnepélyes eredményhirdetésre és díjkiosztásra 2014. november 21-én délután került sor az ELTE Konferenciatermében. Meghívást kaptak az 50 és a 25 évvel ezelőtti Eötvös-verseny nyertesei is. Közülük Corradi Gábor (50 évvel ezelőtti győztes) és Somfai Ellák (25 évvel ezelőtti második díjas) jött el az alkalomra, akik az akkori feladatok ismertetése után röviden beszéltek a versennyel kapcsolatos emlékeikről és pályájukról.
Ezután következett a 2014. évi verseny feladatainak és megoldásainak bemutatása. Az 1. és 3. feladat megoldását Vigh Máté és Gnädig Péter (a feladatok kitűzői), míg a 2. feladatot a külföldi útja miatt távol maradó Tichy Géza helyett Vankó Péter ismertette.
Ezután került sor az eredményhirdetésre. A díjakat Kürti Jenő, az Eötvös Loránd Fizikai Társulat főtitkára adta át.
Egyetlen versenyző se oldotta meg mindhárom feladatot, így a versenybizottság nem adott ki első díjat.
Második díjat nyert és a verseny győztese Öreg Botond, a Budapesti Fazekas Mihály Ált. Isk. és Gimn. 12. osztályos tanulója, Horváth Gábor tanítványa.
Harmadik díjat nyert Fehér Zsombor és Janzer Barnabás, mindketten a Budapesti Fazekas Mihály Ált. Isk. és Gimn. 12. osztályos tanulói, Horváth Gábor tanítványai.
Kiemelt dicséretben részesült Horicsányi Attila, az Egri Dobó István Gimn. érettségizett tanulója, Hóbor Sándor tanítványa, és Takátsy János, a budapesti Városmajori Gimn. érettségizett tanulója, Ábrám László tanítványa ‐ jelenleg mindketten az ELTE fizikus hallgatói.
Dicséretben részesült Morvay Bálint Géza, a pécsi Szent Mór Iskolaközpont érettségizett tanulója, Merényi Péter tanítványa ‐ jelenleg a PTE fizikus hallgatója ‐, Olosz Balázs, a PTE Babits Mihály Gyakorló Gimn. 12. osztályos tanulója, Koncz Károly tanítványa, Szántó András, a debreceni Mechwart András Gépipari és Informatikai Szki. 12. osztályos tanulója, Szőlőssi Irén tanítványa, Tari Balázs, a miskolci Földes Ferenc Gimn. 12. osztályos tanulója, Bíró István és Zámborszky Ferenc tanítványa, valamint Virágh Anna, az Érdi Vörösmarty Mihály Gimn. 12. osztályos tanulója, Varga László és Varga Zsolt tanítványa.
Minden díjazott és felkészítő tanáraik is megkapták az eredményhirdetés előtt néhány nappal megjelent 333 furfangos feladat fizikából című feladatgyűjteményt, amelyet a szerzők ‐ Gnädig Péter, Honyek Gyula és Vigh Máté, az Eötvös-versenybizottság egykori és mostani tagjai ‐ dedikáltak. A MOL támogatásával a második díjjal 25 ezer, a harmadik díjjal 20 ezer, a kiemelt dicsérettel 10 ezer forint pénzjutalom járt, a dicséretesek pedig a Typotex Kiadó által felajánlott könyvet is kaptak.

¹Részletek a verseny honlapján: http://goliat.eik.bme.hu/

\sim

vanko/fizika/eotvos.htm.