Cím:	A 45. Nemzetközi Fizikai Diákolimpiafeladatainak megoldása
Szerző(k):	Tasnádi Tamás ,  Vankó Péter
Füzet:	2014/november, 489 - 504. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   Elméleti feladatok   1. feladat A rész. Az 1. ábra mutatja a kis testre és a csőre ható erőket: az $m$ tömegű kis testre az $mg$ nehézségi erő és az $N$ nyomóerő, az $M$ tömegű csőre az $Mg$ nehézségi erő, a talaj $F$ nyomóereje, az $S$ tapadási súrlódási erő és a kis test által kifejtett $-N$ nyomóerő hat. 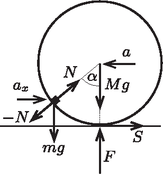  1. ábra. A kis testre és a csőre ható erők     Írjuk fel a mozgásegyenletet a kis test $a_{\text{x}}$ vízszintes (az ábrán jobbra mutató) gyorsuláskomponensére, a cső tömegközéppontjának $a$ (az ábrán balra mutató) gyorsulására és a cső $\beta$ szöggyorsulására: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m{a}_{\text{x}}}& {\displaystyle =N\text{sin}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle Ma}& {\displaystyle =N\text{sin}\alpha -S\mathrm{,}}\hfill \\ \hfill {\displaystyle \Theta \beta }& {\displaystyle =SR\mathrm{,}}\hfill \end{array}}$ ahol $\Theta =M{R}^2$ a cső tehetetlenségi nyomatéka. A cső gyorsulása és szöggyorsulása között a tiszta gördülés miatt fennáll az $a=\beta R$ kapcsolat. Az egyenletrendszert megoldva a testek gyorsulásai között az $m{a}_{\text{x}}=2Ma$ összefüggés adódik. A testek kezdetben nyugalomban voltak, és ez az összefüggés a mozgás során mindvégig fennáll, így a kis test $u$ vízszintes sebességkomponense és a cső $v$ sebessége között is ugyanilyen kapcsolat áll fenn: $mu=2Mv$. A rendszer konzervatív, így teljesül az energiamegmaradás tétele. Az egyenletet a kezdeti állapotra és arra a pillanatra írjuk fel, amikor a kis test éppen legalul van (és csak vízszintes irányban mozog): $\begin{array}{c}{\displaystyle mgR=\frac{m{u}^2}{2}+\frac{M{v}^2}{2}+\frac{\Theta {\omega }^2}{2}\mathrm{,}}\end{array}$ ahol $\omega$ a cső szögsebessége, és a tiszta gördülés miatt $v=\omega R$. Az egyenletekből kifejezhetjük a kis test és a cső sebességét abban a pillanatban, amikor a kis test épp legalul van: ${\displaystyle \begin{array}{c}\hfill {\displaystyle u=2\sqrt[]{\frac{MgR}{2M+m}}\mathrm{,}v=\frac{m}{M}\sqrt[]{\frac{MgR}{2M+m}}\mathrm{.}}\end{array}}$ Vizsgáljuk a kis test mozgását a cső tömegközéppontjával együttmozgó vonatkoztatási rendszerben: itt a kis test $R$ sugarú pályán körmozgást végez. A pálya legalján a sebessége $v_{\text{rel}}=u+v$, centripetális gyorsulása pedig $\begin{array}{c}{\displaystyle a_{\text{cp}}=\frac{v_{\text{rel}}^2}{R}=\frac{{\left(u+v\right)}^2}{R}\mathrm{.}}\end{array}$ Ebben a pillanatban a cső gyorsulása nulla, így a kis test gyorsulása a talajhoz rögzített vonatkoztatási rendszerben is ugyanekkora. Így a kis testre vonatkozó mozgásegyenlet: $m{a}_{\text{cp}}=F-mg$, amiből a keresett $F$ erő: $\begin{array}{c}{\displaystyle F=3mg\left(1+\frac{m}{3M}\right)\mathrm{.}}\end{array}$   B rész. 1) A termodinamika első főtétele alapján a gáz által felvett $\delta Q$ hő $\begin{array}{c}{\displaystyle \delta Q=n{C}_{\text{V}}\text{d}T+p\text{d}V\mathrm{,}}\end{array}$ a keresett $C$ moláris hőkapacitás pedig $\begin{array}{c}{\displaystyle C=\frac{1}{n}\frac{\delta Q}{\text{d}T}=C_{\text{V}}+\frac{p}{n}\frac{\text{d}V}{\text{d}T}\mathrm{.}}\end{array}$ Az egyenletekben $C_{\text{V}}$ az állandó nyomáson mért moláris hőkapacitás, $p$, $n$, $V$ és $T$ pedig a buborékban lévő gáz nyomása, mólszáma, térfogata és hőmérséklete. A Laplace-képlet alapján $\begin{array}{c}{\displaystyle p=\frac{4\sigma }{r}\mathrm{,}}\end{array}$ és eszerint a buborékban lévő gáz állapotváltozása egy olyan politropikus folyamat, melyre $p^{3}V=\text{állandó}$. Ezt összevetve az ideális gáz $pV=nRT$ állapotegyenletével kapjuk, hogy $\begin{array}{c}{\displaystyle T^3{V}^{-2}=\text{állandó,}}\end{array}$ amit differenciálva $\begin{array}{c}{\displaystyle \frac{\text{d}V}{\text{d}T}=\frac{3V}{2T}\mathrm{.}}\end{array}$ Behelyettesítve ezt az eredményt a moláris hőkapacitás képletébe: $\begin{array}{c}{\displaystyle C=C_V+\frac{p}{n}\frac{3V}{2T}=C_V+\frac{3}{2}R\mathrm{,}}\end{array}$ majd felhasználva, hogy a kétatomos gáz állandó térfogaton mért moláris hőkapacitása $\begin{array}{c}{\displaystyle C_V=\frac{5}{2}R\mathrm{,}}\end{array}$ a keresett moláris hőkapacitás $\begin{array}{c}{\displaystyle C=\frac{5}{2}R+\frac{3}{2}R=4R=33\mathrm{,}2\frac{\text{J}}{\text{mol K}}\mathrm{.}}\end{array}$   2) Mivel a gáz hőkapacitása sokkal kisebb, mint a buborék hőkapacitása, valamint a gáz és a buborék között jó hőkontaktus van, a gáz állapotváltozása izotermikusnak tekinthető. Egyensúlyi állapotban a gáz $p$ nyomása megegyezik az $r$ sugarú buborék $p_{\text{g}}$ görbületi nyomásával: $\begin{array}{c}{\displaystyle p=p_{\text{g}}=\frac{4\sigma }{r}\mathrm{.}}\end{array}$ Tekintsük a szappanhártya kicsiny $A$ felületű darabját. Ennek tömege $\begin{array}{c}{\displaystyle m=\rho Ah\mathrm{.}}\end{array}$ Ha a buborék sugarának kicsiny megváltozását $x$-szel jelöljük, akkor a felületdarabkára felírt mozgásegyenlet: $\begin{array}{c}{\displaystyle m\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}\approx \left(p\text{'}-p_{\text{g}}\text{'}\right)A\mathrm{,}}\end{array}$ ahol $p\text{'}$ a gáz nyomása, $p_{\text{g}}\text{'}$ a görbületi nyomás az $r+x$ sugarú buborékban. Az izotermikus állapotváltozás miatt $p\text{'}V\text{'}=pV$, amiből $\begin{array}{c}{\displaystyle p\text{'}=p\frac{1}{{\left(1+\frac{x}{r}\right)}^3}\approx p\left(1-\frac{3x}{r}\right)=p_{\text{g}}\left(1-\frac{3x}{r}\right)\mathrm{.}}\end{array}$ A görbületi nyomás $\begin{array}{c}{\displaystyle p_{\text{g}}\text{'}=\frac{4\sigma }{r+x}\approx p_{\text{g}}\left(1-\frac{x}{r}\right)\mathrm{.}}\end{array}$ Behelyettesítve a mozgásegyenletbe: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \rho Ah\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}=p_{\text{g}}\left(-\frac{2x}{r}\right)A\mathrm{,}\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}=-\frac{8\sigma }{\rho h{r}^2}x\mathrm{,}}\end{array}}$ amiből a rezgés körfrekvenciája $\begin{array}{c}{\displaystyle \omega =\sqrt[]{\frac{8\sigma }{\rho h{r}^2}}=108{\text{s}}^{-1}\mathrm{.}}\end{array}$   C rész. I. megoldás: Abban a pillanatban, amikor a tekercseken át folyó áram maximális, a tekercseken nem esik feszültség. Emiatt a két kondenzátoron azonos nagyságú, ellentétes feszültségnek kell esnie. Jelöljük ebben a pillanatban a kondenzátorok feszültségét $U$-val, a maximális áramerősséget pedig $I_0$-lal. A töltésmegmaradás miatt $q_0=2CU+CU$, amiből a kondenzátorok feszültsége $\begin{array}{c}{\displaystyle U=\frac{q_0}{3C}\mathrm{.}}\end{array}$ Az energiamegmaradás alapján $\begin{array}{c}{\displaystyle \frac{q_0^2}{4C}=\frac{L{I}_0^2}{2}+\frac{2L{I}_0^2}{2}+\frac{C{U}^2}{2}+\frac{2C{U}^2}{2}\mathrm{,}}\end{array}$ amiből pedig a maximális áram $\begin{array}{c}{\displaystyle I_0=\frac{q_0}{3\sqrt[]{2LC}}\mathrm{.}}\end{array}$ Miután a $K$ kapcsolót bezárjuk két, egymástól független rezgőkör alakul ki. Mindkét rezgőkör körfrekvenciája $\begin{array}{c}{\displaystyle \omega =\frac{1}{\sqrt[]{2LC}}\mathrm{.}}\end{array}$ Az egyes rezgőkörökben a rezgés amplitúdóját, azaz az áramerősségek ${\widehat{I}}_1$ és ${\widehat{I}}_2$ maximumát az energiamegmaradás alapján határozhatjuk meg: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{2C{U}^2}{2}+\frac{L{I}_0^2}{2}=\frac{L{\widehat{I}}_1^2}{2}\mathrm{,}\frac{C{U}^2}{2}+\frac{2L{I}_0^2}{2}=\frac{2L{\widehat{I}}_2^2}{2}\mathrm{,}}\end{array}}$ amiből ${\widehat{I}}_1=\sqrt[]{5}{I}_0$, ${\widehat{I}}_2=\sqrt[]{2}{I}_0$. Ha az áram irányát mindkét áramkörben az óramutató járásával egyezőnek vesszük, a kapcsolón átfolyó áram: $I=I_1-I_2$, ahol az $I_1$ és $I_2$ áramok időfüggése: ${\displaystyle \begin{array}{c}\hfill {\displaystyle I_1\left(t\right)=A\text{cos}\omega t+B\text{sin}\omega t\mathrm{,}{I}_2\left(t\right)=D\text{cos}\omega t+F\text{sin}\omega t\mathrm{.}}\end{array}}$ Az $A$ és $D$ konstansok meghatározásához írjuk fel a kezdeti feltételeket: ${\displaystyle \begin{array}{c}\hfill {\displaystyle I_1\left(0\right)=A=I_0\mathrm{,}{I}_2\left(0\right)=D=I_0\mathrm{,}}\end{array}}$ a $B$ és $F$ konstansok meghatározásához pedig a maximális áramerősségeket: ${\displaystyle \begin{array}{c}\hfill {\displaystyle A^2+B^2={\widehat{I}}_1^2\mathrm{,}{D}^2+F^2={\widehat{I}}_2^2\mathrm{,}}\end{array}}$ amiből ${\displaystyle \begin{array}{c}\hfill {\displaystyle B=2I_0\mathrm{,}F=-I_0\mathrm{.}}\end{array}}$ Az $F$ együttható negatív előjele azt fejezi ki, hogy a kapcsoló bekapcsolásának pillanatában a $2L$ induktivitású tekercs árama csökken. Eszerint az egyes rezgőkörök áramának időfüggése: ${\displaystyle \begin{array}{c}\hfill {\displaystyle I_1\left(t\right)=I_0\left(\text{cos}\omega t+2\text{sin}\omega t\right)\mathrm{,}{I}_2\left(t\right)=I_0\left(\text{cos}\omega t-\text{sin}\omega t\right)\mathrm{,}}\end{array}}$ a kapcsolón átfolyó áram időfüggvénye pedig: $\begin{array}{c}{\displaystyle I\left(t\right)=I_1\left(t\right)-I_2\left(t\right)=3I_0\text{sin}\omega t\mathrm{.}}\end{array}$ Ebből a keresett maximális áramerősség: $\begin{array}{c}{\displaystyle I_{\text{max}}=3I_0=\omega q_0=\frac{q_0}{\sqrt[]{2LC}}\mathrm{.}}\end{array}$ II. megoldás: Az $A$, $B$, $D$ és $F$ állandók meghatározása helyett a maximális áramerősséget a 2. ábrán látható vektordiagramból is meghatározhatjuk. A keresett $I_{\text{max}}$ áramerősség nagyságát a $PR$ szakasz hossza határozza meg. 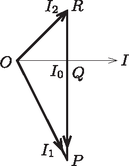  2. ábra. Vektorábra a maximális áram meghatározásához   A kapcsoló bekapcsolásakor az $I_1$ áram növekszik, mert a $2C$ kapacitású kondenzátor továbbra is kisül, míg az $I_2$ áram csökken, hiszen a $C$ kapacitású kondenzátor tovább töltődik. Emiatt az $I_1$ és $I_2$ áramokat az $OP$, illetve az $OR$ vektorok ábrázolják. A vektorok hossza az I. megoldás alapján $\sqrt[]{5}{I}_0$, illetve $\sqrt[]{2}{I}_0$. A kapcsoló bekapcsolásakor mindkét áram nagysága $I_0$, ami az ábrán éppen az $OQ$ szakasz hossza. A Pitagorasz-tétel alapján ebből: ${\displaystyle \begin{array}{c}\hfill {\displaystyle PQ=\sqrt[]{{OP}^2-{OQ}^2}=2I_0\mathrm{,}QR=\sqrt[]{{OR}^2-{OQ}^2}=I_0\mathrm{,}}\end{array}}$ ebből pedig a keresett maximális áramerősség: $\begin{array}{c}{\displaystyle I_{\text{max}}=PR=3I_0=\omega q_0=\frac{q_0}{\sqrt[]{2LC}}\mathrm{.}}\end{array}$   III. megoldás: Mivel a két rezgőkör körfrekvenciája megegyezik, a kapcsolón átfolyó áram körfrekvenciája is ugyanakkora lesz. A kapcsoló zárásakor a rajta átfolyó áram értéke nulla, így a kapcsolón át folyó $I$ áram időfüggvénye: $\begin{array}{c}{\displaystyle I\left(t\right)=I_{\text{max}}\text{sin}\omega t\mathrm{,}\text{ahol}\omega =\frac{1}{\sqrt[]{2LC}}\mathrm{.}}\end{array}$ Mivel a kapcsoló zárásakor ez az áram nulla $\begin{array}{c}{\displaystyle I_{\text{max}}=\frac{\dot{I}}{\omega }\mathrm{,}}\end{array}$ ahol $\dot{I}$ az áram idő szerinti deriváltjának értéke a bekapcsolás pillanatában. Legyen egy adott pillanatban a $2C$ kapacitású kondenzátor töltése $q_1$. Ekkor a másik kondenzátor töltése a töltésmegmaradás miatt $q_2=q_0-q_1$ lesz. A kapcsoló zárása után ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\dot{I}}_1={\omega }^2{q}_1\mathrm{,}{\dot{I}}_2=-{\omega }^2\left(q_0-q-1\right)\mathrm{.}}\end{array}}$ A kapcsolón átfolyó áram idő szerinti deriváltja $\begin{array}{c}{\displaystyle \dot{I}={\dot{I}}_1-{\dot{I}}_2={\omega }^2{q}_0\mathrm{,}}\end{array}$ amiből pedig a keresett maximális áram: $\begin{array}{c}{\displaystyle I_{\text{max}}=\frac{\dot{I}}{\omega }=\omega q_0=\frac{q_0}{\sqrt[]{2LC}}\mathrm{.}}\end{array}$ Ebből a megoldásból az is látszik, hogy a maximális áram értéke független a kapcsoló zárásának időpontjától.   2. feladat. Van der Waals-állapotegyenlet A rész. Reális gázok állapotegyenlete A1. A van der Waals-gáz $\begin{array}{c}{\displaystyle \left(p+\frac{a}{V^2}\right)\left(V-b\right)=RT}\end{array}$ (1) állapotegyenletében szereplő $b$ paraméter egy mólnyi részecske saját térfogatát jelenti, így ha a részecskéket $d$ átmérőjű gömböknek tekintjük, akkor $\begin{array}{c}{\displaystyle b=N_A\frac{4\pi }{3}{\left(\frac{d}{2}\right)}^3=N_A\frac{\pi }{6}{d}^3\mathrm{,}}\end{array}$ (2) ahol $N_A$ az Avogadro-szám. Csak becslésről van szó, hasonló nagyságrendű értéket kapunk, ha a részecskéket $d$ oldalú kockának vagy $d$ sugarú gömbnek tekintjük. A2. A $T_{\text{k}}$ kritikus hőmérséklet fölött minden izoterma mentén a $p$ nyomás szigorúan monoton csökkenő függvénye a $V$ térfogatnak, $T<T_{\text{k}}$ esetén pedig a $p\left(V\right)$ függvénynek van egy növekedő szakasza. A kritikus izotermának a $\left(V_{\text{k}}\mathrm{,}{p}_{\text{k}}\right)$ kritikus pontban vízszintes inflexiós pontja van, tehát $\begin{array}{c}{\displaystyle {\left(\frac{\text{d}p}{\text{d}V}\right)}_{T=T_{\text{k}}}\left(V_{\text{k}}\right)=\mathrm{0,}{\left(\frac{{\text{d}}^{2}p}{\text{d}{V}^2}\right)}_{T=T_{\text{k}}}\left(V_{\text{k}}\right)=0.}\end{array}$ Az (1) állapotegyenlet alapján $\begin{array}{c}{\displaystyle p\left(V\right)=\frac{R{T}_{\text{k}}}{V-b}-\frac{a}{V^2}\mathrm{,}}\end{array}$ ahonnan deriválással a $\begin{array}{c}{\displaystyle -\frac{R{T}_{\text{k}}}{{\left(V_{\text{k}}-b\right)}^2}+\frac{2a}{V_{\text{k}}^3}=\mathrm{0,}\frac{2R{T}_{\text{k}}}{{\left(V_{\text{k}}-b\right)}^3}-\frac{6a}{V_{\text{k}}^4}=0}\end{array}$ egyenletrendszert kapjuk. Innen kifejezhetőek a kritikus állapotjelzők az $a$ és $b$ paraméterek függvényében: $\begin{array}{c}{\displaystyle V_{\text{k}}=3b\mathrm{,}{T}_{\text{k}}=\frac{8a}{27Rb}\mathrm{,}{p}_{\text{k}}=\frac{a}{27b^2}\mathrm{,}}\end{array}$ majd megkaphatók a keresett összefüggések is: $\begin{array}{c}{\displaystyle a=\frac{27R^2{T}_{\text{k}}^2}{64p_{\text{k}}}\mathrm{,}b=\frac{R{T}_{\text{k}}}{8p_{\text{k}}}\mathrm{.}}\end{array}$ (3) A3. A (3) egyenletekbe a megadott $T_{\text{k}}=647$ K és $p_{\text{k}}=2\mathrm{,}2\cdot {10}^7$ Pa értékeket behelyettesítve adódik víz esetén az eredmény: $\begin{array}{c}{\displaystyle a_{\text{víz}}=0\mathrm{,}56\frac{{\text{m}}^6\cdot \text{Pa}}{{\text{mol}}^2}\mathrm{,}{b}_{\text{víz}}=3\mathrm{,}1\cdot {10}^{-5}\frac{{\text{m}}^3}{\text{mol}}\mathrm{.}}\end{array}$ (4) A4. A (2) egyenlet alapján $\begin{array}{c}{\displaystyle d_{\text{víz}}=\sqrt[3]{\frac{6b_{\text{víz}}}{\pi N_A}}=4\mathrm{,}6\cdot {10}^{-10}\text{m. }}\end{array}$ (5)   B rész. Gáz- és folyadékfázis tulajdonságai. Ebben a részben $T=100{}^{\circ }\text{C =373 }\text{K}$ hőmérsékletű, $p_0=1\mathrm{,}0\cdot {10}^5$ Pa nyomású vízzel (illetve vízgőzzel) foglalkozunk, tehát a $T$ és $p_0$ mennyiségek ismert konstansok. A van der Waals-egyenletben szereplő $a$ és $b$ konstansok helyére mindenütt a (4) egyenletben kapott $a_{\text{víz}}$ és $b_{\text{víz}}$ értékeket helyettesítjük. B1. A $b\ll V_{\text{G}}$ feltevés mellett a van der Waals-gáz (1) állapotegyenlete egy $V$-ben másodfokú egyenletre egyszerűsödik: $\begin{array}{c}{\displaystyle \left(P+\frac{a}{V_{\text{G}}^2}\right)V_{\text{G}}=RT\Rightarrow P{V}_{\text{G}}^2-RT{V}_{\text{G}}+a=0.}\end{array}$ Az adott $T=100{}^{\circ }\text{C}$ hőmérsékleten és $p_0=1\mathrm{,}0\cdot {10}^5$ Pa nyomáson a másodfokú egyenlet nagyobbik gyöke adja meg a gőz móltérfogatát, tehát $\begin{array}{c}{\displaystyle V_{\text{G}}=\frac{RT}{2p_0}\left(1+\sqrt[]{1-\frac{4a{p}_0}{R^2{T}^2}}\right)\approx \frac{RT}{p_0}-\frac{a}{RT}=3\mathrm{,}1\cdot {10}^{-2}\frac{{\text{m}}^3}{\text{mol}}\mathrm{.}}\end{array}$ (6) A közelítésnél felhasználtuk, hogy ${\left(1+\epsilon \right)}^{\alpha }\approx 1+\alpha \epsilon$, ha $\left|\epsilon \right|\ll 1$. Esetünkben $\left|\epsilon \right|=\frac{4a{p}_0}{R^2{T}^2}=0\mathrm{,}023\ll 1$, így a közelítés hibája (mely ${\epsilon }^2$-tel arányos) kisebb, mint 1%. Látható, hogy $\frac{V_{\text{G}}}{b}={10}^3$, így valóban teljesül a kiindulásnál használt $b\ll V_{\text{G}}$ feltétel. B2. Az ideális gáz állapotegyenletéből a $V_{\text{G0}}=\frac{RT}{p_0}$ kifejezés adódik a móltérfogatra, így a relatív eltérés $\begin{array}{c}{\displaystyle \frac{\Delta V_{\text{G}}}{V_{\text{G0}}}=\frac{V_{\text{G0}}-V_{\text{G}}}{V_{\text{G0}}}=\frac{1}{2}\left(1-\sqrt[]{1-\frac{4a{p}_0}{R^2{T}^2}}\right)\approx \frac{a{p}_0}{R^2{T}^2}=0\mathrm{,}58=58\%\mathrm{.}}\end{array}$ B3. A belső stabilitást leíró $\frac{\text{d}p}{\text{d}V}<0$ feltétel egyszerűen megérthető; ha ez nem teljesülne, akkor térfogatcsökkenéshez nyomáscsökkenés tartozna, ami újabb térfogatcsökkenést eredményezne, tehát a gáz ,,összeesne'', megindulna a kondenzáció. A gőz állapotban teljesülő $b\ll V$ feltétel mellett a van der Waals gáz nyomása $p\left(V\right)=\frac{RT}{V}-\frac{a}{V^2}$, így a maximális túlhűtéshez tartozó $V_{\text{G, min}}$ minimális móltérfogat a $\begin{array}{c}{\displaystyle {\left(\frac{dP\left(V_{\text{G, min}}\right)}{dV}\right)}_{T=\text{áll.}}=\frac{-RT}{V_{\text{G, min}}^2}+\frac{2a}{V_{\text{G, min}}^3}=0\text{egyenletből}{V}_{\text{G, min}}=\frac{2a}{RT}\mathrm{.}}\end{array}$ A (6) eredmény felhasználásával a keresett hányados: $\begin{array}{c}{\displaystyle \frac{V_{\text{G}}}{V_{\text{G, min}}}\approx \frac{R^2{T}^2}{2a{p}_0}-\frac{1}{2}\approx \frac{R^2{T}^2}{2a{p}_0}=86.}\end{array}$ B4. Folyadék halmazállapotban a móltérfogat kicsi, $p\ll \frac{a}{V_{\text{F}}^2}$, így a van der Waals gáz (1) állapotegyenlete most is egy másodfokú egyenletre egyszerűsödik: $\begin{array}{c}{\displaystyle \frac{a}{V_{\text{F}}^2}\left(V_{\text{F}}-b\right)=RT\Rightarrow RT{V}_{\text{F}}^2-a{V}_{\text{F}}+ab=\mathrm{0,}}\end{array}$ aminek a kisebbik gyöke adja meg a folyadék fajlagos térfogatát: $\begin{array}{c}{\displaystyle V_{\text{F}}=\frac{a}{2RT}\left(1-\sqrt[]{1-\frac{4RTb}{a}}\right)=4\mathrm{,}0\cdot {10}^{-5}\frac{{\text{m}}^3}{\text{mol}}\mathrm{.}}\end{array}$ (7) A kapott értékkel számolva $\frac{a}{p_0{V}_{\text{F}}^2}=3\mathrm{,}5\cdot {10}^3$, tehát valóban teljesül a kiindulásnál használt $p\ll \frac{a}{V_{\text{F}}^2}$ feltétel. B5. A víz sűrűsége: $\begin{array}{c}{\displaystyle {\rho }_{\text{F}}=\frac{\mu }{V_{\text{F}}}=\frac{1\mathrm{,}8\cdot {10}^{-2}\frac{\text{kg}}{\text{mol}}}{4\mathrm{,}0\cdot {10}^{-5}\frac{{\text{m}}^3}{\text{mol}}}=4\mathrm{,}5\cdot {10}^2\frac{\text{kg}}{{\text{m}}^3}\mathrm{.}}\end{array}$ (8) Látható, hogy a kapott érték csak nagyságrendi becslés. B6. Célszerű a (7) kifejezést $T$-ben hatványsorba fejteni. Felhasználva, hogy $\sqrt[]{1-\epsilon }\approx 1-\frac{1}{2}\epsilon -\frac{1}{8}{\epsilon }^2$, ha $\left|\epsilon \right|<1$, $\epsilon =\frac{4RTb}{a}=0\mathrm{,}69$ helyettesítéssel azt kapjuk, hogy $\begin{array}{c}{\displaystyle V_{\text{F}}\approx \frac{a}{2RT}\left(\frac{2RTb}{a}+\frac{2R^2{T}^2{b}^2}{a^2}\right)=b+\frac{RT{b}^2}{a}\approx b\mathrm{.}}\end{array}$ A folyadék móltérfogata első közelítésben a $b$ paraméterrel egyezik meg, ami a részecskék saját térfogata. Az $\epsilon =0\mathrm{,}69$ érték egynél kisebb, de nem jóval kisebb, ezért a közelítés nem igazán pontos; a (7) egyenletben kapott érték mintegy 25%-kal eltér a (4) egyenletben szereplő $b$ értéktől. A térfogati hőtágulási együttható számolásához a $V_{\text{F}}$ másodrendű közelítését kell használni: $\begin{array}{c}{\displaystyle \alpha =\frac{1}{V_{\text{F}}}\frac{\Delta V_{\text{F}}}{\Delta T}=\frac{R{b}^2}{V_{\text{F}}a}\approx \frac{Rb}{a}=4\mathrm{,}6\cdot {10}^{-4}\frac{1}{\text{K}}\mathrm{.}}\end{array}$ B7. A forráshő pontos meghatározásához szükségünk van a van der Waals gáz másik, úgynevezett kalorikus állapotegyenletére, mely az $U$ moláris belső energiát adja meg a hőmérséklet és móltérfogat függvényében: $\begin{array}{c}{\displaystyle U=c_{V}T-\frac{a}{V}\mathrm{,}}\end{array}$ (9) ahol a $c_V$ konstans a gáz állandó térfogaton mért mólhője. A víz (tömegegységre vonatkoztatott) forráshője a termodinamika I. főtételét felhasználva $\begin{array}{c}{\displaystyle L=\frac{Q}{\mu }=\frac{\Delta U-W}{\mu }}\end{array}$ alakban írható, ahol $\mu =1\mathrm{,}8\cdot {10}^{-2}\frac{\text{kg}}{\text{mol}}$ a víz móltömege és $Q$, illetve $W$ egy mól víz elforralásához szükséges hő, illetve munka. Minthogy a forralás során a nyomás és a hőmérséklet állandó, $\begin{array}{c}{\displaystyle \Delta U=U_{\text{G}}-U_{\text{F}}=-\frac{a}{V_{\text{G}}}+\frac{a}{V_{\text{F}}}\mathrm{,}-W=\underset{V_{\text{F}}}{\overset{V_{\text{G}}}{\int }}{p}_0\text{d}V=p_0\left(V_{\text{G}}-V_{\text{F}}\right)\mathrm{.}}\end{array}$ Ezeket beírva a forráshő képletébe, majd figyelembe véve, hogy $V_{\text{F}}\ll V_{\text{G}}$: $\begin{array}{c}{\displaystyle L=\frac{a}{\mu }\left(\frac{1}{V_{\text{F}}}-\frac{1}{V_{\text{G}}}\right)+\frac{p_0}{\mu }\left(V_{\text{G}}-V_{\text{F}}\right)\approx \underset{7\mathrm{,}78\cdot {10}^5\frac{\text{J}}{\text{kg}}}{\overset{}{\underbrace{\frac{a}{\mu V_{\text{F}}}}}}+\underset{1\mathrm{,}72\cdot {10}^5\frac{\text{J}}{\text{kg}}}{\overset{}{\underbrace{\frac{p_0{V}_{\text{G}}}{\mu }}}}=9\mathrm{,}5\cdot {10}^5\frac{\text{J}}{\text{kg}}\mathrm{.}}\end{array}$ (10) Az eredménynek most is csak a nagyságrendje helyes; a víz forráshője $2\mathrm{,}26\cdot {10}^6\frac{\text{J}}{\text{kg}}$. A fenti gondolatmenethez szükséges a (9) egyenlet ismerete, ami nem volt megadva a feladatban, azonban (mélyebb termodinamikai összefüggések felhasználásával) következik (1) állapotegyenletből, és abból a feltételből, hogy híg gáz határesetben a van der Waals gáz viselkedése az ideális gázéhoz közelít. Igen elnagyoltan a következőképpen is eljuthatunk a forráshő becsléséhez. A forraláshoz szükséges hő egyrészt a tágulási munkát fedezi, másrészt az egymással vonzó kölcsönhatásban levő részecskék eltávolításához szükséges. A tágulási munka éppen a (10) egyenlet második tagja. A vonzó kölcsönhatást (1) állapotegyenletben a nyomást korrigáló $\frac{a}{V^2}$ tag írja le, tehát ezen nyomás ellen végzett térfogati munka adja meg a részecskék kölcsönhatási energiájának megváltozását. Ez a (10) egyenlet első tagját adja, hiszen $\begin{array}{c}{\displaystyle \underset{V_{\text{F}}}{\overset{V_{\text{G}}}{\int }}\frac{a}{V^2}\text{d}V={\left[\frac{-a}{V}\right]}_{V_{\text{F}}}^{V_{\text{G}}}=\frac{a}{V_{\text{F}}}-\frac{a}{V_{\text{G}}}\mathrm{.}}\end{array}$ A számértékekből látszik, hogy ez a tag adja a forráshő nagyobb részét. A tágulási munkát elhanyagolva, a $V_{\text{F}}\approx b$ közelítéssel $\begin{array}{c}{\displaystyle L\approx \frac{a}{\mu b}={10}^6\frac{\text{J}}{\text{kg}}}\end{array}$ (11) adódik. B8. Képzeljük el, hogy $m$ tömegű vizet elforralunk, illetve ,,kilapítunk'' egyetlen molekula, azaz $d_{\text{víz}}$ vastagságú réteggé. Első esetben $Lm$ hőt kell befektetnünk. Második esetben a folyadék felszíne $A=\frac{2m}{{\rho }_{\text{F}}{d}_{\text{víz}}}$-re nő, tehát $A\sigma =\frac{2m\sigma }{{\rho }_{\text{F}}{d}_{\text{víz}}}$ munkát kell végeznünk. A két energia jó közelítéssel megegyezik, hiszen mindkettő lényegében a részecskék közti kötések felszakításához szükséges. A korábbi (4), (5), (8) és (11) eredmények felhasználásával: $\begin{array}{c}{\displaystyle Lm\approx \frac{2m\sigma }{{\rho }_{\text{F}}{d}_{\text{víz}}}\Rightarrow \sigma \approx \frac{1}{2}L{\rho }_{\text{F}}{d}_{\text{víz}}\approx \frac{a{d}_{\text{víz}}}{2b^2}=0\mathrm{,}1\frac{\text{N}}{\text{m}}\mathrm{.}}\end{array}$   C rész. Folyadék-gáz rendszer C1. A kapilláris csőben levő vízfelszínre írjuk föl a nyomások egyensúlyát! A víz $h$ mélységben mérhető ${\rho }_{\text{F}}gh$ hidrosztatikai nyomásával tart egyensúlyt a csőben levő gőz ${\rho }_{\text{G}}gh$ hidrosztatikai nyomása és a felületi feszültségből származó $\frac{2\sigma }{r}$ nyomás, tehát $\begin{array}{c}{\displaystyle {\rho }_{\text{F}}gh={\rho }_{\text{G}}gh+\frac{2\sigma }{r}\Rightarrow h=\frac{2\sigma }{\left({\rho }_{\text{F}}-{\rho }_{\text{G}}\right)gr}\approx \frac{2\sigma }{{\rho }_{\text{F}}gr}\mathrm{.}}\end{array}$ A nyomásnövekedés a $h$ magasságú gőzoszlop hidrosztatikai nyomásával egyezik meg, tehát $\begin{array}{c}{\displaystyle \Delta p_T={\rho }_{\text{G}}gh=\frac{2\sigma }{r}\frac{{\rho }_{\text{G}}}{{\rho }_{\text{F}}-{\rho }_{\text{G}}}\approx \frac{2\sigma {\rho }_{\text{G}}}{r{\rho }_{\text{F}}}\mathrm{.}}\end{array}$ (12) C2. A megadott egyenletek alapján a telített vízgőz nyomásának hőmérsékletfüggése: $\begin{array}{c}{\displaystyle p_{\text{FG}}\left(T\right)=e^A\cdot e^{\frac{B}{T}}=\frac{a}{b^2}{e}^{-\frac{a}{bRT}-1}\mathrm{,}}\end{array}$ ahonnan differenciálással azt kapjuk, hogy $\begin{array}{c}{\displaystyle p_{\text{FG}}\left(T_0-\Delta t\right)\approx p_0-p{\text{'}}_{\text{FG}}\left(T_0\right)\Delta t=p_0\left(1-\frac{a\Delta t}{bR{T}_0^2}\right)\mathrm{,}}\end{array}$ tehát $\Delta t=5{}^{\circ }\text{C}$ hőmérséklet-csökkenés esetén a telített gőz nyomása $\Delta p_{\text{FG}}=p_0\frac{a\Delta t}{bR{T}_0^2}$ értékkel csökken. Ugyanakkor a kicsiny $r$ görbületi sugár a (12) egyenlet értelmében megnöveli a telített gőz nyomását. A két egyenlet összevetéséből adódik a cseppképződéshez szükséges minimális görbületi sugár: $\begin{array}{c}{\displaystyle \Delta p_T=\Delta p_{\text{FG}}\Rightarrow \frac{2\sigma {\rho }_{\text{G}}}{r{\rho }_{\text{F}}}=p_0\frac{a\Delta t}{bR{T}_0^2}\Rightarrow r=\frac{2\sigma {\rho }_{\text{G}}bR{T}_0^2}{a{p}_0{\rho }_{\text{F}}\Delta t}\mathrm{.}}\end{array}$ Ha a telített gőzt ideális gáznak tekintjük, akkor sűrűsége ${\rho }_{\text{G}}=\frac{\mu p_0}{R{T}_0}$, a folyadék víz sűrűsége pedig korábbi (8) eredményünk alapján ${\rho }_{\text{F}}\approx \frac{\mu }{b}$. Ezeket felhasználva a következő eredményt kapjuk: $\begin{array}{c}{\displaystyle r=\frac{2\sigma b^2}{a}\frac{T_0}{\Delta t}=1\mathrm{,}5\cdot {10}^{-8}\text{m. }}\end{array}$   3. feladat. A gázkisülés legegyszerűbb modellje A rész. Nem önfenntartó gázkisülés A1. Minthogy az elektronok és ionok párokban keletkeznek, sűrűségük minden időpillanatban megegyezik, $n_{\text{e}}\left(t\right)=n_{\text{i}}\left(t\right)=n\left(t\right)$. Az elektronok sűrűsége a külső besugárzás miatt nő, a rekombináció miatt csökken, így az $\begin{array}{c}{\displaystyle \dot{n}\left(t\right)=Z_{\text{ext}}-Z_{\text{rek}}=Z_{\text{ext}}-r{n}^2}\end{array}$ differenciálegyenlet írható föl. A feladat szerint az egyenlet megoldását $n\left(t\right)=n_0+a\text{tgh}\left(bt\right)$ alakban kereshetjük. Az $n\left(0\right)=0$ kezdeti feltétel miatt $n_0=0$. Ezután az $n\left(t\right)=a\text{tgh}\left(bt\right)$ függvényt beírva a differenciálegyenletbe, figyelembe véve, hogy $\text{tgh}\text{'}x=\frac{1}{\text{ch}{}^{2}x}$, valamint, hogy $\text{ch}{}^{2}x-\text{sh}{}^{2}x=1$, rövid számolás után azt kapjuk, hogy $\begin{array}{c}{\displaystyle a=\sqrt[]{\frac{Z_{\text{ext}}}{r}}\mathrm{,}b=\sqrt[]{r{Z}_{\text{ext}}}\mathrm{.}}\end{array}$ A2. Egyetlen, $Z_{\text{ext}}$ erősségű külső ionizáló esetén az egyensúlyi elektronsűrűség $\begin{array}{c}{\displaystyle n_{\text{e}}=\underset{t\to \infty }{\overset{}{\text{lim}}}a\text{tgh}\left(bt\right)=a=\sqrt[]{\frac{Z_{\text{ext}}}{r}}\mathrm{,}}\end{array}$ (13) ahonnan $Z_{\text{ext}}=r{n}_{\text{e}}^2$, tehát két ionizálót együtt használva $Z_{\text{ext}\mathrm{,1}}+Z_{\text{ext}\mathrm{,2}}=r{n}_{\text{e}}^2$, így $\begin{array}{c}{\displaystyle n_{\text{e}}=\sqrt[]{\frac{Z_{\text{ext}\mathrm{,1}}}{r}+\frac{Z_{\text{ext}\mathrm{,2}}}{r}}=\sqrt[]{n_{\text{e1}}^2+n_{\text{e2}}^2}=2\cdot {10}^{11}\frac{1}{{\text{cm}}^3}\mathrm{.}}\end{array}$ A3. Minthogy az elektronok és ionok sűrűsége és mobilitása is megegyezik, a két töltéshordozó mozgásából származó elektromos áram is megegyezik, tehát $I=I_{\text{e}}+I_{\text{i}}=2I_{\text{e}}$. Az $L$ hosszú, $S$ keresztmetszetű csőben levő elektronok száma egyrészt a besugárzás miatt $LS{Z}_{\text{ext}}$-tel nő, másrészt, a rekombináció, illetve a kiáramlás miatt $SLr{n}_{\text{e}}^2$-tel, illetve $vS{n}_{\text{e}}$-vel csökken időegységenként. Egyensúly esetén az elektronok száma nem változik, tehát $\begin{array}{c}{\displaystyle SL{Z}_{\text{ext}}-SLr{n}_{\text{e}}^2-vS{n}_{\text{e}}=0.}\end{array}$ Felhasználva, hogy az elektronok driftsebessége $v=\beta E=\beta \frac{U}{L}$, a másodfokú egyenlet pozitív megoldása $n_{\text{e}}$-re: $\begin{array}{c}{\displaystyle n_{\text{e}}=\frac{\beta U}{2r{L}^2}\left(\sqrt[]{1+\frac{4r{L}^4{Z}_{\text{ext}}}{{\beta }^2{U}^2}}-1\right)\mathrm{.}}\end{array}$ (14) A keresett áramerősség: $\begin{array}{c}{\displaystyle I=2I_{\text{e}}=2e{n}_{\text{e}}vS=\frac{eS{\beta }^2{U}^2}{r{L}^3}\left(\sqrt[]{1+\frac{4r{L}^4{Z}_{\text{ext}}}{{\beta }^2{U}^2}}-1\right)\mathrm{.}}\end{array}$ (15) A4. Kis $U$ feszültség esetén (15) kifejezésben a gyökjel alatti második tag mellett az első, $+1$ tag, és a gyökvonás után a $-1$ is elhanyagolható, tehát ekkor $\begin{array}{c}{\displaystyle I\approx \frac{eS{\beta }^2{U}^2}{r{L}^3}\sqrt[]{\frac{4r{L}^4{Z}_{\text{ext}}}{{\beta }^2{U}^2}}=\frac{2eS\beta U}{L}\sqrt[]{\frac{Z_{\text{ext}}}{r}}\mathrm{.}}\end{array}$ (Ugyanezt az eredményt kapjuk akkor is, ha a (15) egyenletben az $n_{\text{e}}$ elektronsűrűség helyére nem a (14) kifejezést, hanem a zérus feszültség mellett kapott (13) értéket helyettesítjük.) Ezt felhasználva a gáz fajlagos ellenállása: $\begin{array}{c}{\displaystyle \rho =\frac{US}{IL}=\frac{1}{2e\beta }\sqrt[]{\frac{r}{Z_{\text{ext}}}}\mathrm{.}}\end{array}$   B rész. Önfenntartó gázkisülés. Ebben a részben az egyensúlyi áramot tanulmányozzuk, így az elektronok $n_{\text{e}}$ és az ionok $n_{\text{i}}$ sűrűsége nem függ az időtől, viszont az elektronlavina miatt függ a helytől. A feladat feltevése értelmében az $E=\frac{U}{L}$ elektromos tér a cső mentén homogén, és az elektronok valamint ionok sebessége $v=\beta E$ állandó. B1. Ahogy a feladatban szerepel, az $x$ tengely mutasson az $L$ hosszúságú gázcső mentén a növekvő elektromos potenciál irányába, azaz az elektronok mozgásának irányába. Az $x$ és $x+\text{d}x$ közti szeletben levő elektronok száma egyrészt a besugárzás miatt $Z_{\text{ext}}S\text{d}x$-szel, az elektronok beáramlása miatt $vS{n}_{\text{e}}\left(x\right)$-szel, az elektronlavina miatt pedig $\alpha vS{n}_{\text{e}}\left(x\right)\text{d}x$-szel nő, másrészt, az elektronok kiáramlása miatt $vS{n}_{\text{e}}\left(x+\text{d}x\right)$-szel csökken időegységenként. Állandósult áramlás esetén azonban a teljes elektronszám nem változik, tehát $\begin{array}{c}{\displaystyle 0=\underset{\text{besugárzás}}{\overset{}{\underbrace{Z_{\text{ext}}S\text{d}x}}}+\underset{\text{beáramlás}}{\overset{}{\underbrace{vS{n}_{\text{e}}\left(x\right)}}}+\underset{\text{elektronlavina}}{\overset{}{\underbrace{\alpha vS{n}_{\text{e}}\left(x\right)\text{d}x}}}-\underset{\text{kiáramlás}}{\overset{}{\underbrace{vS{n}_{\text{e}}\left(x+\text{d}x\right)}}}\mathrm{.}}\end{array}$ Az egyenletet $\text{d}x$-szel osztva, és felhasználva, hogy az elektronok által képviselt áram $I_{\text{e}}\left(X\right)=evS{n}_{\text{e}}\left(x\right)$, az $\begin{array}{c}{\displaystyle I{\text{'}}_{\text{e}}\left(x\right)=eS{Z}_{\text{ext}}+\alpha I_{\text{e}}\left(x\right)}\end{array}$ differenciálegyenletet kapjuk, melybe behelyettesítve a megadott $I_{\text{e}}\left(x\right)=C_1{\text{e}}^{A_{1}x}+A_2$ kísérletező függvényt, rövid számolás után az ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A_1=\alpha \mathrm{,}{A}_2=-\frac{eS{Z}_{\text{ext}}}{\alpha }\mathrm{,}{I}_{\text{e}}\left(x\right)=C_1{\text{e}}^{\alpha x}-\frac{eS{Z}_{\text{ext}}}{\alpha }}& \text{(<mn>16</mn>)}\end{array}}$ eredmények adódnak. (A képletekben $e$ az elemi töltés, $\text{e}$ pedig az Euler-féle szám.) B2. Gondolatmenetünk az elektronáram esetéhez hasonló; állandósult áramlás esetén az $x$ és $x+\text{d}x$ közti szeletben az ionok száma nem változik, tehát $\begin{array}{c}{\displaystyle 0=\underset{\text{besugárzás}}{\overset{}{\underbrace{Z_{\text{ext}}S\text{d}x}}}-\underset{\text{kiáramlás}}{\overset{}{\underbrace{vS{n}_{\text{i}}\left(x\right)}}}+\underset{\text{elektronlavina}}{\overset{}{\underbrace{\alpha vS{n}_{\text{e}}\left(x\right)\text{d}x}}}+\underset{\text{beáramlás}}{\overset{}{\underbrace{vS{n}_{\text{i}}\left(x+\text{d}x\right)}}}\mathrm{.}}\end{array}$ (Az ionok ellentétes mozgása miatt a második és negyedik tag előjele megváltozott, és az elektronlavinát leíró tagban nem $n_{\text{i}}$, hanem továbbra is $n_{\text{e}}$ szerepel!) Innen az elektronáramra kapott (16) eredményt is felhasználva az $\begin{array}{c}{\displaystyle I{\text{'}}_{\text{i}}\left(x\right)=-eS{Z}_{\text{ext}}-\alpha I_{\text{e}}\left(x\right)=-\alpha C_1{\text{e}}^{\alpha x}}\end{array}$ összefüggés adódik, amit az adott $I_{\text{i}}\left(x\right)=C_2+B_1{\text{e}}^{B_{2}x}$ formulával összevetve a ${\displaystyle \begin{array}{cc}\hfill {\displaystyle B_1=-C_1\mathrm{,}{B}_2=\alpha \mathrm{,}{I}_{\text{i}}\left(x\right)=C_2-C_1{\text{e}}^{\alpha x}}& \text{(<mn>17</mn>)}\end{array}}$ eredményhez jutunk. B3. Mivel az anódból nem lépnek ki ionok, ezért $I_{\text{i}}\left(L\right)=0$. B4. A másodlagos elektronkeltés definíciójának értelmében $I_{\text{e}}\left(0\right)=\gamma I_{\text{i}}\left(0\right)$. B5. Az előző két pontban kapott határfeltételekbe beírva a (16) és (17) formulákat megkaphatjuk a hiányzó $C_1$ és $C_2$ együtthatókat: $\begin{array}{c}{\displaystyle }\end{array}$ C2-C1eαL=0C1-eSZextα=γ(C2-C1) }⇒ C1=eSZextα⋅11+γ(1-eαL)C2=eSZextα⋅1e-αL(1+γ)-γ. A teljes áram az ionok és az elektronok járulékának összege. Ahogy várjuk, ez már nem függ az $x$ helytől, és értéke: $\begin{array}{c}{\displaystyle I=I_{\text{e}}\left(x\right)+I_{\text{i}}\left(x\right)=C_2-\frac{eS{Z}_{\text{ext}}}{\alpha }=\frac{eS{Z}_{\text{ext}}}{\alpha }\left(\frac{1}{{\text{e}}^{-\alpha L}\left(1+\gamma \right)-\gamma }-1\right)\mathrm{.}}\end{array}$ (18) B6. Elég hosszú cső esetén az elektronlavinából keletkező elektronok elegendő töltéshordozót biztosítanak az áram fenntartásához (sőt, növeléséhez) külső gerjesztés nélkül is. A (18) képletből látszik, hogy ahogy $L$ értékét növeljük, $I$ nő, és $L\nearrow L_{\text{kr}}$ esetén $I\to \infty$. Az $L_{\text{kr}}$ kritikus hossz a (18) képletben szereplő tört nevezőjének zérushelye: $\begin{array}{c}{\displaystyle {\text{e}}^{-\alpha L_{\text{kr}}}\left(1+\gamma \right)-\gamma =0\Rightarrow L_{\text{kr}}=\frac{1}{\alpha }\text{ln}\left(\frac{1+\gamma }{\gamma }\right)\mathrm{.}}\end{array}$   Kísérleti feladat: Látni a láthatatlant A mérési feladat címe és témája nagyon izgalmas: Az optikai anizotrópia jelensége lehetővé teszi, hogy polarizált fény segítségével megfigyeljünk ,,láthatatlan'' jelenségeket. (Sajnos a mérési eszközök kivitelezése és a feladatok nem elég részletes megfogalmazása a versenyzők többségének megnehezítette a mérés elvégzését és a jelenségek megértését.) Sok anyag optikailag anizotrop, ami azt jelenti, hogy a törésmutató függ a fényterjedés és a polarizáció irányától. Optikailag izotrop anyag is anizotroppá válhat mechanikai feszültség, egyenetlen melegítés vagy külső elektromos tér hatására. A kristály optikai tengelyének azt az irányt nevezzük, amely mentén a fény a kristályban kettőstörés nélkül halad. A 3. ábrán látható a kettőstörés jelenségét vizsgáló optikai elrendezés vázlata. 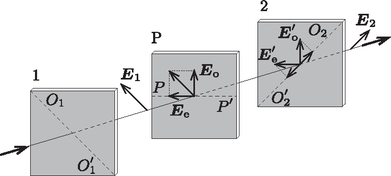  3. ábra. Az optikai anizotrópia vizsgálatára szolgáló elrendezés vázlata   A fénysugár az 1-es polárszűrőre esik, melynek áteresztési síkja az $O_1{O}_1\text{'}$ egyenesben metszi a polárszűrő síkját. Az 1-es polárszűrőn való áthaladás után a fény lineárisan poláros lesz, és az ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1$ elektromos térerősség vektora az 1-es polarizátor áteresztési síkjában fog rezegni. Ezután a fény az anizotrop P lemezre esik, melynek $PP\text{'}$ irányú optikai tengelye ${45}^{\circ }$-os szöget zár be az 1-es polárszűrő átengedési síkjával. A P lemezben ekkor két különböző fényhullám keletkezik: az ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_{\text{o}}$ ordinárius sugár polarizációs iránya a lemez optikai tengelyére merőleges, az ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_{\text{e}}$ extraordinárius sugáré pedig azzal párhuzamos. A két hullámra vonatkozó törésmutató különbözik, különbségük: $\Delta n=n_{\text{o}}-n_{\text{e}}$. Emiatt a két hullám között a lemezen való áthaladás és a kilépés után $\Delta \phi =2\pi h\Delta n/\lambda$ fáziskülönbség lesz ($h$ a lemez vastagsága, $\lambda$ a fény hullámhossza vákuumban), és így a kilépő fény elliptikusan poláros lesz. Ez a fénysugár esik a 2-es polárszűrőre, melynek $O_2{O}_2\text{'}$ áteresztési síkja merőleges az 1-es polárszűrő áteresztési síkjára. Könnyen belátható, hogy a P lemezen és a 2-es polárszűrőn áthaladó fény intenzitása $\begin{array}{c}{\displaystyle I_2=k{I}_0\text{sin}{}^2\frac{\Delta \phi }{2}\mathrm{,}}\end{array}$ ahol $I_0$ a lemezre eső fény intenzitása, $k$ a P lemez és a 2-es polarizátor fényáteresztési együtthatója, $\Delta \phi$ pedig az ordinárius és extraordinárius sugár közti fáziskülönbség a P lemezen való áthaladás után.   1. rész: Kvalitatív megfigyelés A versenyzőknek először kvalitatív megfigyeléseket kellett végezniük. Ebben a részben egy fehér LED volt a fényforrás, és a 3. ábrán látható elrendezésben a két egymásra merőleges áteresztési síkú polárszűrő közé különböző műanyag vonalzókat, görbült fóliacsíkot és folyadékkristály cellát (LCC) kellett helyezni, majd a megfigyelt jelenségeket leírni. A vonalzókban a mechanikai feszültség, a görbült fóliasíkban a változó vastagság, az LCC-ben a rákapcsolt feszültség hatására változó optikai anizotrópia figyelhető meg. (A folyadékkristály az anyag olyan állapota, mely a kristályos szilárd és amorf folyadék között van. A folyadékkristály molekuláinak orientációja könnyen állítható és szabályozható elektromos térrel. A folyadékkristály cella optikailag anizotrop, kétféle törésmutatója van. A jelenség mértéke függ az alkalmazott váltakozó feszültségtől. Az LCC két üveglapból áll, melyek belső felületét átlátszó vezető réteg borítja. A lemezek közt van egy körülbelül $10\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>μ</mi></math>m}$ vastagságú folyadékkristály oldat. A lemezekhez kivezetéseket forrasztanak, amivel egy tápegységre lehet kapcsolni őket. Ha nem kapcsolunk rá feszültséget, a folyadékkristály hosszú molekulái a lemezekkel párhuzamosak. (A hosszúkás molekulák iránya egybeesik a kristály optikai tengelyével.) Mivel a jelenségek hullámhosszfüggők, a fényforrás fehér fényének összetevői különböző mértékben gyengülnek: színes csíkok és foltok jelennek meg.   2. rész: A mérés A feladat második, hosszabb részében kvantitatív méréseket végeztek a versenyzők. A fehér LED helyett egy (piros) lézerdióda volt a fényforrás, az átmenő fény intenzitását pedig egy fotodetektorral lehetett mérni. A fotodetektor egy fotodiódából, egy terhelő ellenállásból és egy voltmérőből áll. Először ezt az eszközt kellett vizsgálni: megállapítani, hogy milyen terhelő ellenállással működik optimálisan. Ezután az így beállított eszközzel különböző anizotrop anyagokon végezhettek méréseket a diákok. A műanyag vonalzókban a gyártás során mechanikai feszültség keletkezik, amely az anyagban helytől függő anizotrópiát okoz. Emiatt a vonalzót a  3. ábrán látható mérési elrendezéssel vizsgálva a hely függvényében változó intenzitás mérhető. Ebből meg lehet határozni az ordinárius és extraordinárius sugár közti $\Delta \phi$ fáziskülönbség helyfüggését. A tapasztalat szerint a fáziskülönbség a hely lineáris függvénye, ami viszont az intenzitás szinusznégyzetes változását okozza. A mérésben ennek a szinusznégyzetes függvénynek egy kis darabja mérhető ki, és ebből lehetett következtetni a fáziskülönbségre (ami nem volt könnyű feladat). Ezután a versenyzőknek egy folyadékkristály cellát kellett vizsgálniuk. A cella anizotrópiája akkor maximális, ha a cella nem kap feszültséget. Ha a cellára egyre nagyobb (váltó)feszültséget kapcsolunk, az anizotrópia (a törésmutatók közötti különbség, és így a fázistolás) monoton (de nemlineárisan) csökken, és emiatt az átmenő intenzitás nulla és egy maximális érték között oszcillál. A mérés alapján közvetlenül ez az oszcilláló függvény (az intenzitás a cellára kapcsolt feszültség függvényében) rajzolható fel, majd ebből lehet következtetni a maximális fázistolás nagyságára és a fázistolás feszültségtől való függésére. (A feszültségfüggés a tapasztalat szerint egy bizonyos tartományban hatványfüggvény: a versenyzőknek a hatványfüggvény kitevőjét is meg kellett határozniuk.) Az utolsó mérési feladat egy görbült fóliacsík vizsgálata volt. Ebben az esetben az anyag anizotrópiája mindenhol ugyanakkora volt, de a görbület miatt a fény a fóliacsík különböző helyein más-más utat tesz meg a fóliacsíkon belül, és emiatt itt is helyfüggő fáziskülönbség alakul ki. Mérni most is az intenzitás változását lehetett, és ismét ebből kellett következtetni a fáziskülönbség változására (minden részfeladatban ez a legnehezebb lépés). A mérés alapján meghatározható a nem görbülő fóliacsík fázistolása, valamint a fóliacsík görbületi sugara. 1Az elméleti feladatok szövegét a múlt havi számunkban közöltük.