Kezdőlap


Cím:	Beszámoló a 2013. évi Eötvös-versenyről
Szerző(k):	Honyek Gyula , Radnai Gyula , Vankó Péter , Vigh Máté
Füzet:	2014/március, 165 - 174. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2013. október 18-án délután 3 órai kezdettel rendezte meg az Eötvös Loránd Fizikai Társulat 65. Eötvös-versenyét. A versenyen részt vehetett bárki, aki 2013-ban fejezte be középiskolai tanulmányait, vagy ebben az évben is középiskolába járt. Az öt óra (300 perc) megoldási idő alatt a versenyzők bármely magukkal hozott írott vagy nyomtatott segédeszközt használhattak a feladatok megoldásához, zsebszámológépen kívül azonban minden más elektronikus segédeszköz használata tilos volt.
Idén először az ország határain kívül, az angliai Cambridge-ben is megrendezésre került a verseny, az időeltolódás miatt ott délután 2 órai kezdettel. Itthon a szokásos helyszíneken készültek fel a Társulat munkatársai a versenyzők fogadására, sajnos azonban három városban egyetlen diák sem jelent meg a versenyen. Budapesten 62, a többi helyszínen összesen 49 dolgozatot adtak be, melyeket a feladatokat kitűző Eötvös-versenybizottság bírált el. Tagjai Honyek Gyula, Vankó Péter és Vigh Máté voltak, elnöke pedig Radnai Gyula. Az összesen 111 dolgozat közül 27-et írtak elsőéves, javarészt a BME-re és az ELTE-re járó egyetemi hallgatók. A középiskolás versenyzők közül a legtöbben a budapesti Fazekas (16 fő), a szegedi Radnóti (12 fő) és a budapesti Radnóti (6 fő) gimnáziumból jöttek. Volt öt külföldi, nem magyar állampolgárságú versenyző is.
Ismertetjük a feladatokat és azok megoldását.

*

1. feladat. Két viszonylag hosszú, tömegükben és külső méreteikben megegyező merev test közül az egyik alumíniumból készült, tömör, egyenes henger, a másik rézből készült, egyenletes falvastagságú cső. A testeket kemény, jól tapadó lejtőre helyezzük úgy, hogy tengelyük vízszintes legyen.

1. ábra

a)

Milyen magasból kell elengednünk az egyes testeket, hogy 1 m/s haladási sebességgel érjék el a lejtő alját?
A lejtőt 1 m/s sebességgel elhagyó testek lassulva gördülnek tovább egy puhább, hosszú, vízszintes felületen. A testek a felület kicsiny benyomódása miatt fékeződnek. Tételezzük fel, hogy a vízszintes felület által a testekre ható eredő erő pillanatnyi támadáspontja a hengerpalástokon mindkét esetben ugyanott helyezkedik el!

b)

Az alumíniumhenger a vízszintes felületen 2 m út megtétele után áll meg. Hol áll meg a rézcső?
Adatok: az alumínium sűrűsége

2, 7 {g/cm}^{3}

, a réz sűrűsége

8, 9 {g/cm}^{3}

(Honyek Gyula)

Megoldás.

a)

h

magasságból elengedett testek gravitációs helyzeti energiája a lejtő alján mozgási energiává alakul:

\begin{matrix} m g h = \frac{1}{2} m v^{2} + \frac{1}{2} Θ ω^{2} = \frac{1}{2} m v^{2} + \frac{1}{2} k m R^{2} \frac{v^{2}}{R^{2}}, \end{matrix}

ahol

m

a testek tömege,

R

a sugaruk, a tehetetlenségi nyomatékot pedig

Θ = k m R^{2}

alakban írtuk fel. Felhasználtuk továbbá, hogy a tiszta gördülés miatt a testek tömegközéppontjának

v

sebessége és a forgásuk

ω

szögsebessége között fennáll a

v = R ω

kényszerfeltétel. Ebből az indítási magasságra a következő adódik:

\begin{matrix} h = \frac{v^{2}}{2 g} (1 + k) . \end{matrix}

A tömör alumíniumhenger esetében

k_{Al} = 1 / 2,

vagyis

h_{Al} = 3 v^{2} / (4 g) = 7, 6

cm.
A rézcső tömege is, külső sugara is megegyezik az alumíniumhenger adataival. Így kifejezhetjük a rézcső belső

r

sugarát

R

segítségével:

\begin{matrix} \frac{R^{2}}{R^{2} - r^{2}} = \frac{ϱ_{Cu}}{ϱ_{Al}} \to r^{2} = \frac{(ϱ_{Cu} - ϱ_{Al})}{ϱ_{Cu}} R^{2} . \end{matrix}

A rézcső tehetetlenségi nyomatékát

\begin{matrix} Θ_{Cu} = \frac{1}{2} ϱ_{Cu} π ℓ (R^{4} - r^{4}) \end{matrix}

alakban írhatjuk fel, ahol

ℓ

a hengeres testek hosszúsága. Kihasználhatjuk, hogy tömegek megegyeznek, ennek alapján a rézcső tehetetlenségi nyomatékra a következőt kapjuk:

\begin{matrix} Θ_{Cu} = \frac{1}{2} m R^{2} (1 + \frac{ϱ_{Cu} - ϱ_{Al}}{ϱ_{Cu}}) = \frac{2 ϱ_{Cu} - ϱ_{Al}}{2 ϱ_{Cu}} m R^{2} . \end{matrix}

A kapott eredményből leolvasható, hogy

\begin{matrix} k_{Cu} = \frac{1}{2} \frac{2 ϱ_{Cu} - ϱ_{Al}}{ϱ_{Cu}} = 0, 85, \end{matrix}

tehát

\begin{matrix} h_{Cu} = \frac{2 (1 + k_{Cu})}{3} h_{Al} = 9, 4 cm . \end{matrix}

b)

A kissé puha felületen a hengeres testekre a nehézségi erő mellett a felület fejt ki erőt, melynek támadáspontja mindkét test esetén ugyanoda esik. A felület által kifejtett kényszererő (ezt szaggatott nyíl jelöli) két összetevőre bontható: a függőleges összetevő nagysága

m g

(ezt szokás nyomóerőnek hívni), míg a vízszintes összetevőt jelöljük

S

-sel (ez felel meg a tapadási súrlódási erőnek).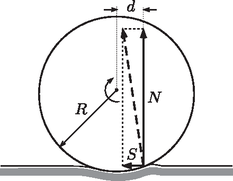

2. ábra

A kényszererő függőleges összetevője hatásvonalának és a hengeres test középpontjának a távolsága legyen

d

, a vízszintes felületen megtett utat pedig jelöljük

x

-szel. A testek tömegközéppontjának gyorsulását a dinamika alapegyenlete írja le:

\begin{matrix} \sum F = m a . \end{matrix}

Az alumíniumhenger esetén a vízszintes irányú gyorsulást az

S_{Al}

súrlódási erő okozza:

\begin{matrix} S_{Al} = m a_{Al} = m \frac{v^{2}}{2 x_{Al}}, \end{matrix}

ahol

v = 1

m/s és

x_{Al} = 2

m.
A tiszta gördülés miatt a henger szöggyorsulása

β_{Al} = a_{Al} / R

. Ezt a szöggyorsulást a forgómozgás alapegyenlete értelmében a testre ható erők (tömegközéppontra vonatkoztatott) forgatónyomatékának eredője hozza létre:

\begin{matrix} \sum M = Θ β . \end{matrix}

Írjuk fel a forgómozgás alapegyenletét az alumíniumhengerre, majd fejezzük ki a

d

távolságot:

\begin{matrix} M = m g d - S_{Al} R = m g d - m \frac{v^{2}}{2 x_{Al}} R = Θ_{Al} β_{Al} = \frac{1}{2} m R^{2} \frac{a_{Al}}{R} = \frac{1}{2} m R^{2} \frac{v^{2}}{2 x_{Al} R}, \end{matrix}

amiből

\begin{matrix} d = \frac{3 v^{2}}{4 g x_{Al}} R . \end{matrix}

A rézcső esetén a tapadási súrlódási erő más lesz (és természetesen a tehetetlenségi nyomaték is más), de a többi mennyiség ugyanaz marad. Újra fel kell írnunk a haladó mozgásra és a forgásra a dinamikai alapegyenleteket:

\begin{matrix} S_{Cu} & = m a_{Cu} = m \frac{v^{2}}{2 x_{Cu}}, \\ M & = m g d - S_{Cu} R = m g d - m \frac{v^{2}}{2 x_{Cu}} R = Θ_{Cu} β_{Cu} = \\ = k_{Cu} m R^{2} \frac{a_{Cu}}{R} = k_{Cu} m R^{2} \frac{v^{2}}{2 x_{Cu} R}, \end{matrix}

amiből

\begin{matrix} d = \frac{(1 + k_{Cu}) v^{2}}{2 g x_{Cu}} R . \end{matrix}

A kétféleképpen kifejezett

d

távolság összevetéséből a rézcső útja a vízszintes felületen:

\begin{matrix} x_{Cu} = \frac{2 (1 + k_{Cu})}{3} x_{Al} = 2, 46 m . \end{matrix}

Megjegyzések. 1. Vegyük észre, hogy ahányszor magasabbról indítottuk a rézcsövet, annyiszor messzebb áll meg a vízszintes felületen. Ezt úgy is interpretálhatjuk, hogy a teljes mechanikai energia a kezdeti magassággal arányos, és a mechanikai energia ,,hővé alakulása'' (disszipációja) pedig a vízszintes szakaszon megtett úttal arányos. Azonban ez az energiadisszipáció nem írható fel a súrlódási erő és a megtett út szorzataként, hiszen ha így írnánk fel, akkor mindkét testre ugyanakkora súrlódási erőt kapnánk, ami nyilvánvalóan hamis következtetés lenne. Az energia nem a szokásos csúszási súrlódás formájában disszipálódik (gyakorlatilag tiszta gördülés történik, lényegében tapadó súrlódás lép fel), hanem a testek alatti felület nem tökéletesen rugalmas benyomódása okozza a mechanikai energiaveszteséget. Feltehetjük, hogy mindkét test esetén ugyanolyan széles és ugyanolyan mély a benyomódás, ezért tapasztalhatjuk azt, hogy a disszipáció a nyom hosszával arányos.
2. Érdemes észrevennünk azt is, hogy a felületre merőleges nyomóerő forgatónyomatéka lassítja a testek forgását, míg a súrlódási erő gyorsítja a forgást. A súrlódási erő kicsi, de az erőkarja (

R

) nagy (a benyomódás mértéke elhanyagolható a sugárhoz képest), míg a nyomóerő jelentős, de az erőkarja (

d

) kicsi. Az alumíniumhenger esetén a súrlódási erő a nyomóerőnek (

m g

-nek) hozzávetőlegesen 1/40 része, a rézcsőnél mindössze 1/50 része. A

d

távolság a sugárnak nagyjából 3/80 része, tehát a nyomóerő forgatónyomatéka az alumíniumhenger esetén másfélszer akkora, mint a súrlódási erő nyomatéka (a rézcsőnél ez az arány másfélnél valamivel nagyobb). Ez azt mutatja, hogy a kétféle nyomaték összemérhető.
3. A számításokban a képletek leegyszerűsítése érdekében a gyorsulások és a szöggyorsulások abszolút értékével számoltunk, miközben természetesen nyilvánvaló, hogy a vízszintes felületen a testek gyorsulása is, szöggyorsulása is negatív.
4. Az eredményhirdetésen az első feladat megoldásának ismertetése után a hallgatóság egy valódi kísérletről készült videófelvételen láthatta, hogy egy tömör alumíniumhenger és egy ugyanolyan tömegű, illetve ugyanolyan külső méretű rézcső a példa megoldásának megfelelően nem egyforma úton lassul le vízszintes felületen, ha azonos kezdősebességgel, tisztán gördülve, egyszerre indítjuk őket. A puha felületet egy asztallapra leterített abrosz szolgáltatta, az azonos sebességű, egyidejű indítás egy hosszú vonalzóval történt.

2. feladat. Egy furcsa optikai rácson a rések nem egyenlő közönként helyezkednek el: a szomszédos rések távolsága felváltva

30 μ m

és

90 μ m

. Milyen elhajlási kép alakul ki a 2 m távolságra elhelyezett ernyőn, ha a rácsot (annak síkjára merőlegesen) 660 nm hullámhosszúságú lézerfénnyel világítjuk meg? Ábrázoljuk vázlatosan az ernyőn kialakuló intenzitáseloszlást! (A rések szélessége egyforma és sokkal kisebb a távolságuknál.)

(Vigh Máté)

Megoldás. Először képzeljük el, milyen lenne a diffrakciós kép, ha minden második rést (a másodikat, negyediket stb.) kitakarnánk! Ekkor a

4 d

távolságra elhelyezkedő rések egy szokásos optikai rácsot alkotnának, az

n

-edik elhajlási maximum ernyőn mérhető

x_{n}

helyzetét pedig a

\begin{matrix} 4 d sin α_{n} & = n λ, \\ sin α_{n} & \approx x_{n} / L \end{matrix}

összefüggések alapján számíthatjuk:

\begin{matrix} x_{n} = n \frac{λ L}{4 d} . \end{matrix}

(

*

)

3. ábra

Ugyanilyen lenne az elhajlási kép, ha a másik réssort (azaz az első, harmadik stb. rést) takarnánk ki. A feladatban kérdezett esetre visszatérve meg kell vizsgálnunk, hogy a (

*

) egyenlet által meghatározott irányokban hogyan adódik össze a két,

d

távolsággal eltolt,

4 d

periódusú réssoron áthaladó fény amplitúdója. Négy esetet kell megvizsgálnunk:

•

n = 4 k + 1

, akkor a két réssoron áthaladó fény közötti útkülönbség

λ / 4

, ami

π / 2

fáziskülönbségnek felel meg. Két,

π / 2

fáziskülönbséggel találkozó, azonos amplitúdójú hullám összegének amplitúdója (rögzített helyen):

\begin{matrix} E_{0} sin (ω t) + E_{0} sin (ω t + π / 2) = E_{0} sin (ω t) + E_{0} cos (ω t) = \\ = \sqrt[]{2} E_{0} (\frac{1}{\sqrt[]{2}} sin (ω t) + \frac{1}{\sqrt[]{2}} cos (ω t)) = \sqrt[]{2} E_{0} sin (ω t + π / 4) . \end{matrix}

Az amplitúdó tehát az egy réssoron átjutó fény amplitúdójának

\sqrt[]{2}

-szerese, azaz az intenzitás az egy réssor esetében mérhető intenzitás kétszerese.

$•$	Ha $n = 4 k + 2$ , akkor a két réssor közötti fáziskülönbség $π$ , tehát ilyen irányokban tökéletes kioltást tapasztalunk.

$•$	Ha $n = 4 k + 3$ , a fáziskülönbség $3 π / 2$ , így az amplitúdó (az első esethez hasonlóan) az egyetlen réssoron áthaladó fény amplitúdójának $\sqrt[]{2}$ -szerese, az intenzitás pedig a kétszerese lesz.

$•$	Ha $n = 4 k$ , akkor minden sugár erősíti egymást, az amplitúdó tehát egyetlen réssoron áthaladó fény amplitúdójának kétszerese, az intenzitás pedig négyszerese lesz.

Összefoglalva: a 4. ábrán látható intenzitáseloszlás alakul ki, a nagy intenzitású maximumok közötti távolság

λ L / d

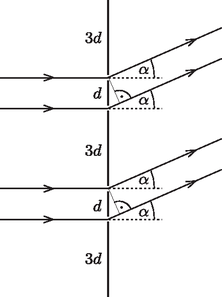
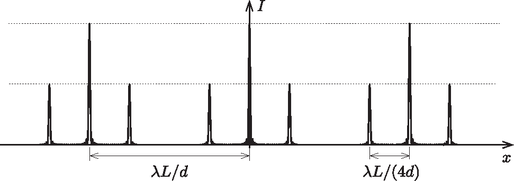4. ábra

Megjegyzések. 1. Optikai ráccsal keltett diffrakciós (elhajlási) kép esetén az ernyőn kialakuló vonalak rendkívül keskenyek, ezek a vonalak meglehetősen ,,élesek''. A közepes vonalszélesség jó közelítésben annyiad része két egymás utáni vonal távolságának, ahány résből áll a rács. Ez pedig legalább száz, de akár sok ezer is lehet.
2. A második feladat megoldásának a bemutatását is kísérleti szemléltetés követte. A feladat szövegének megfelelő optikai rácsot Kis Lajos (Szeged) készítette el a következő módon. A rács (arányosan megnövelt méretű) mintázatát számítógépes rajzolóprogram segítségével egy A/3 méretű lapra nyomtatta, majd a lapot megfelelő távolságból elegendően finom szemcseméretű filmre fényképezte. A lapra nyomtatott vékony, sötét vonalak a filmnegatívon áteresztő résekként jelentek meg. Az eredményhirdetésen a lézerrel megvilágított rács elhajlási képe az elméleti számításokkal megegyező módon, jól láthatóan jelent meg a terem vetítőernyőjén.

3. feladat.

B

indukciójú, homogén, erős mágneses térben egy

ℓ

hosszúságú, könnyű, vékony, hajlékony vezetőhuzal végpontjait az egymástól

ℓ / 2

távolságra lévő

P_{1}

és

P_{2}

pontokban rögzítettük. A huzalon

I

erősségű egyenáramot vezetünk át. Milyen alakot vesz fel a vezeték, ha a mágneses indukcióvektor

a)

merőleges a

P_{1} P_{2}

szakaszra?

b)

párhuzamos a

P_{1} P_{2}

szakasszal?

Mekkora erővel húzza a vezeték a rögzítési pontokat az egyes esetekben?

(Vigh Máté)

Megoldás.

a)

A vezetőhuzal a mágneses térerősségre merőleges síkban fog elhelyezkedni. Mivel a mágneses tér által a vezető darabkáira kifejtett erő mindenhol merőleges a huzalra, ezért a vezeték minden pontjában ugyanakkora erő ébred. A vezeték

r

görbületi sugarú darabkájában

F = I B r

nagyságú erő ébred. Ez könnyen belátható a vezeték kis darabkájára ható erők vizsgálatával (5. ábra).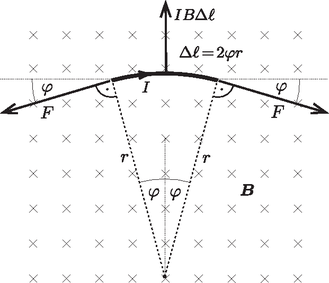

5. ábra

Az erőegyensúly:

\begin{matrix} 2 F sin φ = I B Δ ℓ . \end{matrix}

Geometriából:

\begin{matrix} Δ ℓ = 2 φ r . \end{matrix}

A kis szögek miatt

sin φ \approx φ

, ebből valóban az

F = I B r

eredményre jutunk. Az eddigiekből következik, hogy a huzal körív alakot vesz fel. (Elvben a többmenetes ,,körtekercs'' alak is egyensúlyi helyzet, ez azonban labilis, így nem is alakítható ki, ahogy egy ceruzát sem lehet a hegyére állítani.)
A körívre a következő geometriai összefüggéseknek kell teljesülniük (6. ábra):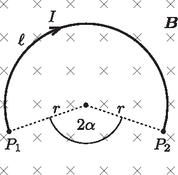

\begin{matrix} 2 r sin α & = ℓ / 2, \\ 2 r (π - α) & = ℓ, \end{matrix}

ezekből a

2 sin α = π - α

transzcendens egyenletre jutunk, melynek numerikus megoldása

α \approx 1, 246 rad = 71, 40^{\circ}

. Ezt visszaírva a fenti egyenletekbe a kör sugarára

r \approx 0, 26 ℓ

, a vezetéket feszítő erőre pedig

F \approx 0, 26 I B ℓ

értéket kapunk.

6. ábra

b)

Ebben az esetben a vezetőhuzal darabkáira nem hat a mágneses térerősséggel párhuzamos irányú erő, ezért a vezetéket feszítő erő

B

-irányú komponense állandó. A mágneses mező által a vezető darabkáira kifejtett erő mindenhol merőleges a huzalra, ezért a vezeték minden pontjában ugyanakkora erő ébred. E két tényből következik, hogy a vezetéket feszítő erő mágneses térerősségre merőleges komponense állandó kell legyen, azaz a mágneses térerősség irányából nézve a vezetékre egy kört fogunk látni, a huzal alakja pedig egyenletes menetemelkedésű, a mágneses térerősséggel párhuzamos tengelyű, egymenetes csavarvonal lesz (lásd a 7. ábrát). (Elvben a többmenetes csavarvonal alak is egyensúlyi helyzet, ez azonban könnyen beláthatóan labilis.)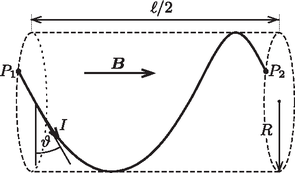

7. ábra

A csavarvonal menetemelkedésének

ϑ

szögét (azaz a csavarvonal adott pontbeli érintője és az ugyanezen ponton átmenő, a

B

-térre merőleges sík által bezárt szöget) egyszerű geometriával számíthatjuk ki:

\begin{matrix} sin ϑ = \frac{ℓ}{2 ℓ}, ebből ϑ = 30^{\circ} . \end{matrix}

A csavarvonalra illeszkedő, képzeletbeli hengerpalást

R

sugara:

\begin{matrix} R = \frac{ℓ cos ϑ}{2 π} = \frac{\sqrt[]{3} ℓ}{4 π} \approx 0, 138 ℓ . \end{matrix}

Most térjünk rá az erő kiszámítására! A csavarvonal tengelyének irányából nézve azt látjuk, hogy az

R

sugarú, teljes körnek látszó vezetéket a mágneses Lorentz-erő próbálja szétfeszíteni, ezt ellensúlyozza a vezetékben ébredő erőnek a mágneses térerősségre merőleges

F cos ϑ

nagyságú komponense:

I B R = F cos ϑ

. Felhasználva

R

kifejezését megkapjuk a vezetéket feszítő erőt:

\begin{matrix} F = \frac{I B ℓ}{2 π} \approx 0, 159 I B ℓ . \end{matrix}

Látszik, hogy a huzalban ébredő erő független a

P_{1}

és

P_{2}

pontok

d

távolságától (

0 < d < ℓ

Megjegyzés. A verseny eredményhirdetésén a 3. feladatban szereplő kísérleti elrendezés is bemutatásra került. A kísérlet megvalósítása egyszerű körülmények között nehéz, több gyakorlati nehézségbe is ütközik.
A feladat szövegében homogén, erős mágneses tér szerepel. Ezt a két feltételt nem könnyű egyszerre teljesíteni. Aránylag nagy térrészben homogén és erős mágneses teret csak nagyon nagy (és drága) eszközökkel lehet előállítani. A kísérleti bemutatón a tér előállítására Helmholtz-tekercset használtunk¹, melynek tere a tekercsek közti tér közepén elég jó közelítéssel homogén ‐ viszont nem túl erős. (A Föld mágneses terénél azért egy-két nagyságrenddel nagyobb.)
A feladat szövegében szereplő vezeték könnyű, vékony és hajlékony. A szövegben a ,,könnyű'' azt jelenti, hogy a vezeték súlya elhanyagolható a mágneses tér által kifejtett erőhöz képest. (Az ,,erős mágneses tér'' pedig arra utal, hogy a vezeték saját mágneses terének hatását is elhanyagolhatjuk.) A feltételek teljesítéséhez nagyon vékony vezetéket kellett használnunk: egy kb. 0,1 mm vastag vörösréz huzalt, amely olyan vékony, hogy alig látszik. A huzal vastagsága viszont korlátozza a vezetéken átfolyó áram nagyságát is, pedig a nem túl erős mágneses tér mellett minél nagyobb áramra van szükség a jelenség bemutatásához. Az áramerősséggel elmentünk a határokig: a vezeték (miután leégett róla a szigetelő lakk) vörösen izzott ‐ és így az elsötétített teremben láthatóvá is vált.
A bemutatón először egy, a feladathoz lazábban kapcsolódó kísérletet mutattunk be: egy kisnyomású héliummal töltött csőben figyeltük meg az elektronok mozgását. Az izzókatódból kilépő, felgyorsított elektronok a Helmholtz-tekercsben kör-, illetve csavarvonal alakú pályán mozognak, és pályájuk a gerjesztett héliumatomok zöld fényének köszönhetően látható².
Ezután vizsgáltuk a vezeték alakját. Még egy ilyen vékony vezeték is aránylag merev (tehát a hajlékonyságot se könnyű biztosítani), de a feladat

a)

részének megfelelő elrendezésben az áram bekapcsolásakor jól láthatóan kör alakban kifeszült, az áramirány változtatásakor pedig a körív

180^{\circ}

-kal átfordult. A vezeték végeinek

90^{\circ}

-os elforgatásakor (a feladat

b)

részének megfelelő elrendezésben) jól megfigyelhetően kialakult a csavarvonal forma. (A feladatban kérdezett kicsiny erők mérésére ebben az egyszerű demonstrációban természetesen nem volt lehetőség.)

*

Az ünnepélyes eredményhirdetésre és díjkiosztásra 2013. november 15-én délután került sor az ELTE Konferenciatermében. Meghívást kaptak az 50 és a 25 évvel ezelőtti Eötvös-verseny nyertesei is. 50 évvel ezelőtt Tichy Géza nyerte meg a versenyt, Abos Imre lett a második, Major János a harmadik. Mindhárman itt voltak ‐ Tichy Géza az ELTE-ről, Abos Imre a BME-ről, Major János Stuttgartból jött el. 25 évvel ezelőtt már nemcsak érettségizettek indulhattak az Eötvös-versenyen, s az első tíz helyezett felvételi nélkül kerülhetett be az egyetemre. Ennek megfelelően a résztvevők és a díjazottak száma is nagyobb volt. A két akkori első díjas közül Fucskár Attila eljött, Hauer Tamás levelet küldött mostani munkahelyéről, a CERN-ből. Volt tanárával, Tarnócziné Gedeon Melittával együtt jelent meg a második díjas Demeter Gábor, és eljött a harmadik díjas Keleti Tamás is, aki ma az ELTE Analízis Tanszékének vezetője. Felesége és két kisgyereke kísérte el Somfai Ellákot, aki akkor dicséretet kapott dolgozatára.
A versenybizottság elnöke megemlékezett Radó Tiborról, aki 100 éve, 1913-ban, és Hlucsil Károlyról, aki 1911-ben lett I. díjas ezen a versenyen. Ezután kivetítette az 1963. és az 1988. évi feladatokat, valamint az akkori nyertesek közül a KöMaL-ban is eredményesen szereplő diákok egykori fényképeit. Felkérésére mindannyian szóltak néhány szót emlékeikről, azóta befutott pályájukról. Ezután következett a 2013. évi feladatok ismertetése. A megoldásokat azok mutatták be, akik kitalálták ezeket a feladatokat. Honyek Gyula az 1. feladathoz kapcsolódó kísérletről videót is vetített. A 2. feladathoz kapcsolódó kísérletet Vigh Máté mutatta be egy olyan optikai ráccsal, amely erre az alkalomra készült. A 3. feladat megoldását is Vigh Máté ismertette, a hozzá kapcsolódó kísérletet azonban már Vankó Péter állította össze és mutatta be.
Ezután Radnai Gyula felkérte Zawadowski Alfréd akadémikust, az Eötvös Loránd Fizikai Társulat elnökét a 2013. évi Eötvös-verseny díjainak átadására.
Az első díjat mindhárom feladat hibátlan megoldásáért Szabó Attila nyerte, aki jelenleg Cambridge-ben természettudomány szakos egyetemi hallgató. Pécsett érettségizett a Leőwey Klára Gimnáziumban, tanára Simon Péter, szakkörvezetője Kotek László volt. Ők vették át az első díjat Attila helyett, akivel viszont sikerült Skype-on egyidejűleg kapcsolatba lépnünk, és akit így kivetítve láthattak és tapsolhattak meg a többiek.
Második díjat nyert egyenlő helyezésben Fehér Zsombor, a Budapesti Fazekas Mihály Általános Iskola és Gimnázium 11. évf. tanulója, Horváth Gábor tanítványa, valamint Kovács Áron Dániel, az Eötvös Loránd Tudományegyetem fizika szakos hallgatója, aki ugyancsak a Fazekas Gimnáziumban érettségizett mint Horváth Gábor és Csefkó Zoltán tanítványa.
Harmadik díjat nyert egyenlő helyezésben Horicsányi Attila, az egri Dobó István Gimnázium 12. évf. tanulója, Hóbor Sándor tanítványa, Janzer Barnabás, a Budapesti Fazekas Mihály Általános Iskola és Gimnázium 11. évf. tanulója, Horváth Gábor tanítványa, valamint Takátsy János, a budapesti Városmajori Gimnázium 12. évf. tanulója, Ábrám László tanítványa.
Dicséretet kapott Holczer András, a pécsi Janus Pannonius Gimnázium 11. évf. tanulója, tanára a gimnáziumban Dombi Anna, szakkörvezetője Kotek László, valamint Öreg Botond, a Budapesti Fazekas Mihály Általános Iskola és Gimnázium 11. évf. tanulója, akinek Horváth Gábor és Szokolai Tibor voltak a tanárai.
A MOL támogatásával az első díjjal 30 ezer, a második díjjal 20 ezer, a harmadik díjjal 15 ezer forint pénzjutalom járt, míg a dicséretesek Simonyi Károly A fizika kultúrtörténete c. művének legújabb kiadását kapták meg. A díjazottak megjelent tanárai és a megjelent 50, illetve 25 évvel ezelőtti nyertesek egy-egy értékes könyvet választhattak maguknak az ELFT, a MATFUND Alapítvány, a Nemzeti Tankönyvkiadó, a Typotex Kiadó és az Akkord Kiadó kiállított könyvei közül.
Befejezésül a Versenybizottság leköszönő elnöke értékelte az idei versenyt és felsorolta mindazokat az intézményeket, vállalatokat és magánszemélyeket, amelyek, illetve akik anyagi segítségével sikerült a Társulatnak az elmúlt 25 évben lebonyolítania a versenyt.
Zawadowski Alfréd megköszönte Radnai Gyulának a Versenybizottságban több mint 40 éve, elnökként pedig 25 éve végzett munkáját, és átnyújtott egy oklevelet, mely tanúsítja, hogy elnyerte ,,az Eötvös-verseny Versenybizottságának örökös tiszteletbeli elnöke'' címet.
Az ünnepélyes díjkiosztást jó hangulatú állófogadás zárta a Ramasoft Zrt. jóvoltából.

¹http://fizipedia.bme.hu/images/a/a7/Helmholtz2.jpg

²http://fizipedia.bme.hu/images/9/90/Eperm5.jpg