Cím: Matematika és fizika totó megoldása
Füzet: 2014/január, 49 - 55. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
Matematika és fizika totó megoldása1
 

A telitalálatos szelvény:
2,X,2,X,2,1,2,2,1,1,2,X,X,2.
Az alábbiakban rövid útmutatást adunk a feladatok megoldásához.
1. Húzzuk először (nem feltétlenül egyforma nagy erővel) a mászórudat és a kötelet úgy, hogy az aljuk ugyanolyan magasra emelkedjék. Mivel ilyenkor a mászórúd tömegközéppontja biztosan távolabb van a felfüggesztési ponton átmenő függőlegestől, mint a kötélé, a mászókötél ilyen helyzetben tartásához kisebb erő szükséges, mint a rúdnál alkalmazott erő. Ha ezekután a kötélre kifejtett erőt megnöveljük annyira, hogy a rudat húzó erővel egyforma nagy legyen, a kötél vége magasabbra emelkedik, mint a rúd alja.
 
2. Hívjuk a hangya két irányváltoztatás között megtett útját ,,lépés''-nek. Így azt kell megmutatnunk, hogy amennyiben a hangya visszaért kiindulási pontjába, akkor lépéseinek száma osztható 4-gyel.
Világos, hogy a hangya visszatéréséig ugyanannyiszor lépett balra, mint jobbra, összesen tehát páros sokat lépett vízszintesen. Ugyanez igaz a függőleges irányú lépéseire is.
Ha a hangya kezdő lépésének irányával párhuzamosan érkezett volna vissza, akkor a lépésenkénti irányváltoztatás miatt eggyel kevesebbszer lépett volna erre az irányra merőlegesen, mint vele párhuzamosan, így vagy a vízszintes, vagy pedig a függőleges lépéseinek a száma páratlan volna. Láttuk viszont, hogy e két szám páros, hangyánk tehát csak az indulási irányra merőlegesen fejezhette be útját. Ebből következik, hogy ugyanannyit lépett vízszintesen, mint függőlegesen. Lépéseinek a száma tehát egy páros szám kétszerese, így valóban osztható 4-gyel.
A megadott válaszok közül csak a 100 olyan többszöröse az 5-nek, melyben a szorzó oszható 4-gyel.
 
3. Megmutatjuk, hogy három instabil oldallapú homogén tetraéder nincsen. (Kevesebb instabil oldallappal rendelkező viszont nyilvánvalóan létezik. Például egy ,,erősen tompaszögű'' háromszög alapú, ,,nagyon ferde'' gúla két lapjáról is felborul.)
Ha a tetraédernek valamelyik lapja instabil, akkor átbillenéskor a súlypontja alacsonyabbra kerül. Egy tetraéder súlypontjának magassága a tetraéder magasságának negyedénél található, így minél nagyobb területű lapján fekszik a tetraéder, a súlypont annál alacsonyabban helyezkedik el. Belátjuk: ha valamelyik oldallap instabil, akkor létezik a tetraédernek legalább két másik oldallapja, amelyek területe nagyobb, mint a kérdéses lap területe. Ebből már következik, hogy a legnagyobb és a második legnagyobb területű oldallap stabil kell legyen.
Egy homogén tetraéder súlypontjának s helyvektorát az
s=14(a+b+c+d)
módon számíthatjuk ki a tetraéder csúcsaiba mutató a, b, c és d vektorok segítségével. A tetraédernek az ABC lapja akkor instabil, ha a tetraéder súlypontjának s helyvektorának az ABC síkra eső s' vetülete az ABC háromszögön kívülre esik.
Tegyük fel, hogy a tetraéder ABC lapja instabil, és legyen az origó az ABC háromszög S súlypontja! Ekkor a+b+c=0, így s=d/4. Nagyítsuk fel az ABC háromszöget az S súlypontjából centrálisan a négyszeresére! Az ABC oldallap borulékonysága miatt a d vektor ABC síkra vett d' vetületének végpontja kívül esik a felnagyított A'B'C' háromszögön.
 

1. ábra

 

Könnyen belátható, hogy AM=MP, ezért a BC és B'C' egyenesek távolsága ugyanakkora, mint az A csúcs és a BC egyenes távolsága. Ugyanez igaz a többi oldalra is. Ebből következik, hogy a D csúcs D' vetülete kívül esik az A'B'C' háromszögön, tehát egyik oldalélének ‐ mondjuk B'C'-nek ‐ az ABC háromszöggel ellentétes oldalára kerül.
Megmutatjuk, hogy ehhez a tetraédernek legalább két oldallapja nagyobb területű, mint az alaplap t(ABC) területe. t(BCD')>t(ABC), hiszen D' messzebb van BC-től, mint az A pont. Másrészt t(BCD)>t(BCD'), mert a BCD' háromszöget a BCD-ből vetítéssel állítottuk elő. Tehát a BCD háromszög területe nagyobb, mint az ABC háromszög területe. Az ábrából leolvashatóan az is fennáll, hogy
t(ABD')+t(ACD')≥t(ABC)+t(BCD')>2⋅t(ABC),
tehát az ABD' és ACD' háromszögek valamelyike is biztosan nagyobb területű, mint az alaplap, a hozzá tartozó tetraéderlap pedig (a vetítés miatt) még nagyobb. Találtunk tehát két olyan oldallapot (BCD, valamint ABD és ACD közül az egyik), amelynek területe nagyobb, mint az instabil ABC oldallapé.
Ezzel beláttuk, hogy egy homogén tetraédernek legalább két stabil oldallapja kell legyen.
 
4. A keresett szám fele és harmada is egész, így az előbbi 3-mal osztható négyzetszám, utóbbi pedig 2-vel osztható köbszám. A szám fele így osztható 32=9-cel. Maga a szám emiatt 2⋅9=18-cal és 3⋅8=24-gyel, vagyis a 18 és a 24 legkisebb közös többszörösével, 72-vel is osztható.
A 72 fele 36, ami négyzetszám, ezért a keresett szám a 72-nek négyzetszámszorosa. Azt a legkisebb négyzetszámot kell tehát még megkeresnünk, amellyel 72:3=24-et megszorozva köbszámot kapunk. Mivel 24=23⋅3, minden alkalmas szorzó osztható 32=9-cel, e szorzók legkisebbike pedig a 9.
A keresett szám tehát a 9⋅72=648. Ennek a fele 324, ami 18-nak a négyzete, harmada pedig 216, ami 6-nak a köbe.
Megjegyzés. A megoldás során többször is felhasználtuk azt az egyáltalán nem nyilvánvaló tényt, hogy egy szám négyzetében és köbében ugyanazok a prímtényezők szerepelnek, mint a számban, illetve hogy előbbiben minden egyes prímtényező kitevője páros, utóbbiban pedig minden kitevő osztható 3-mal.
A fentiek a ,,számelmélet alaptételének'' nevezett állítás következményei, mely szerint pozitív egész számok csak egyféleképpen bonthatók fel prímszámok szorzatára.
 
5. A kihűlés ,,időállandója'' a test méretétől (R), sűrűségétől (ϱ), fajhőjétől (c) és a környezet hővezetőképességétől (σ) függ(het). (Feltételezzük, hogy maga a test a környezeténél sokkal jobb hővezető, pl. fém, emiatt a test hővezetőképességét nem soroltuk fel a lényeges paraméterek között.) Ezen adatokból idő dimenziójú mennyiség T∝ϱcR2/σ módon képezhető, ami azt mutatja, hogy a kihűlés ,,ideje'' erősen függ a test méretétől. Különböző alakú, de azonos ,,átlagos'' méretű testek ‐ mint azt egyszerű geometriájú konkrét példákon láthatjuk ‐ általában más-más ütemben hűlnek. A hőmérsékletkülönbség ,,feleződési ideje'' tehát általában a test méretétől is és az alakjától is függ.
 
6. Számozzuk meg a perselyeket, illetve a hozzájuk illő kulcsokat 1-től 10-ig, ezután helyezzük el a kulcsokat a zárt perselyekben, majd állítsuk sorba a perselyeket. A feltétel szerint ekkor a 10 kulcsnak 10!-féle egyenlően valószínű sorrendje lehetséges. Minden egyes sorrendnek a kulcsok egy részének a kihúzási sorrendje felel meg, nekünk azoknak a sorrendeknek a számára van szükségünk, amikor valamennyi perselyt fel tudjuk nyitni, tehát az összes kulcsot kihúztuk.
Egy adott elhelyezés esetén pontosan akkor akadunk el, ha már nyitva van az a persely, amelynek a kulcsa éppen a kezünkbe került. Maga a kulcs ekkor csak az 1-es számú, feltört persely kulcsa lehet, hiszen erőszakoskodás nélkül felnyitott persely kulcsa nem lehet későbbi perselyben. Amennyiben tehát valamennyi perselyt fel tudjuk nyitni, akkor harmincadiknak az 1-es számú, feltört persely kulcsát húzzuk ki. Hívjuk a kulcsok ilyen sorrendjeit a perselyekben jó sorrendnek.
Mármost a kulcsok minden lehetséges S=(s1,s2,...,s10) kihúzási sorrendjének ‐ ahol tehát s10=1 ‐ megfeleltethető a kulcsoknak egy olyan S*=(s1*,s2*,...,s10*) jó sorrendje a perselyekben, melynek során éppen az S sorrendben férünk hozzá a kulcsokhoz. Nyilván
s1*=s1,ss1*=s2,ss2*=s3,...,ss8*=s9,ss9*=s10=1.

Az S↔S* megfeleltetés jól láthatóan kölcsönösen egyértelműen képezi le az 1-gyel végződő permutációk halmazát a jó sorrendek halmazára, így éppen annyi jó sorrend van, mint ahányféleképpen sorba rakhatjuk a 10 darab kulcsot úgy, hogy az 1-es számú álljon az utolsó helyen. Mivel pedig az ilyen sorrendek száma éppen 9!, a keresett valószínűség 9!10!=110.
 
7. A hőmérséklet növekedtével a hajszálrugó hossza is és a billegőkerék átmérője is megnő. Emiatt a rugó direkciós nyomatéka (egységnyi szögelforduláshoz szükséges forgatónyomaték) lecsökken, a billegőkerék tehetetlenségi nyomatéka pedig megnő. Mindkét változás növeli a torziós lengések periódusidejét, emiatt az óra (hacsak valamilyen trükkös mechanizmussal ki nem egyenlítik ezt a hatást) késni fog.
 
8. Megmutatjuk, hogy a feltétel éppen a derékszögű háromszögekre teljesül. Eközben felhasználjuk a következő két, nyilvánvaló állítást:
(*) A magasságszakasz felezőpontja rajta van a magasságra merőleges középvonal egyenesén.
(**) Ha egy egyenes nem megy át egy adott háromszög egyik csúcsán sem, akkor a háromszög oldalai közül páros sokat metsz belső pontban, tehát vagy kettőt, vagy pedig egyet sem.
A megoldásra térve legyen először az ABC háromszög A csúcsánál derékszög. Ekkor az AB és az AC befogók egyúttal magasságok is. A felezőpontjukat összekötő egyenes éppen a BC oldallal párhuzamos középvonal, ezen pedig a (*) állítás miatt rajta van az A csúcsból induló magasságszakasz felezőpontja is. Derékszögű háromszög magasságszakaszainak felezőpontjai tehát valóban egy egyenesen vannak.
Most belátjuk, hogy hegyes- vagy tompaszögű háromszögre a feltétel nem teljesül.
Ha a háromszög hegyesszögű, akkor mindhárom magasságszakasz a háromszög belsejében van, így a három felezőpont a középvonalháromszög egy-egy oldalának belső pontja. Ha ezek egy egyenesen volnának, akkor ez az egyenes a középvonalháromszögnek három oldalát metszené belső pontban, ami (**) miatt lehetetlen.
Ha a háromszög tompaszögű, akkor két magasságszakasz a háromszögön kívül, egy pedig azon belül halad. A három felezőpont közül ezért kettő a középvonalháromszög egy-egy oldalegyenesén, de az oldalszakaszon kívül, egy pedig a harmadik oldalszakaszon belül található. Ha tehát a három felezőpont egy egyenesen volna, akkor ez az egyenes a középvonalháromszögnek pontosan egy oldalát metszené belső pontban, ami (**) miatt ismét nem lehet.
Ezzel állításunkat beláttuk.
 
9. Azt kell megvizsgálnunk, hogy mekkora munkát végzünk, miközben a fonál hosszát valamekkora h távolsággal lecsökkentjük. Ha ez a munka mgh-val, vagyis az ingatest helyzeti energia-növekedésével lenne egyenlő, akkor a lengés amplitúdója nem változna.
Ténylegesen a végzett munka nagyobb, mint mgh, emiatt a lengések amplitúdója nőni fog. Igaz ugyan, hogy az mg nehézségi erőnek csak mgcosφ≤mg komponense járul hozzá a fonálerőhöz, viszont a centripetális gyorsuláshoz szükséges mv2/ℓ ,,többleterőt'' is a fonálnak kell fedeznie. (Itt φ(t)=φmaxsinωt az inga kitérése, v(t)=φmaxℓωcosωt a lengő test pillanatnyi sebessége, ω=g/ℓ pedig az aktuális ingahosszhoz tartozó körfrekvencia.) A fonalat feszítő erő (kis szögkitérések esetén)
K(t)=mgcosφ+mv2ℓ≈mg(1-φ22)+mv2ℓ=mg+mgφmax2(-cos2ωt2+sin2ωt).
Az utolsó tagban szereplő zárójeles kifejezés (felülvonással jelölt) időbeli átlaga pozitív, hiszen sin2φ¯=cos2φ¯=12, így valóban K(t)¯>mg, vagyis a lengések szögamplitúdója növekszik.
 
10. Ha köbre emeljük az eredeti egyenlet mindkét oldalát és a bal oldalt az
(a+b)3=a3+b3+3ab(a+b)(1)
azonosság szerint alakítjuk át, akkor rendezés után a
32x+134-x3(2x+13+4-x3)=-(x+8)(2)
egyenlethez jutunk. Itt (1) alapján a bal oldali zárójelben -33 áll, és így
33(2x+1)(4-x)3=x+8.(3)

Ismét köbre emelve és rendezve a harmadfokú
x3+186x2-375x+188=0(4)
egyenletet kapjuk. A bal oldalon az együtthatók összege nulla, az egyenletnek tehát gyöke az 1, így az (x-1) tényező kiemelése után a kapott másodfokú polinomot szorzattá alakítva végül az
(x-1)2(x+188)=0(5)
egyenlet adódik. Ennek két gyöke van, az 1 és a -188. Az eredeti egyenletnek az 1 nem megoldása, hiszen ha x=1, akkor a bal oldal pozitív, a jobb oldal pedig negatív. A (-188) megoldása az (1) egyenletnek.
 
11. A víz felszíne az új egyensúlyi helyzetben a Föld és az égi jövevény együttes potenciális energiájának szintfelülete kell legyen. A Föld gravitációs potenciálja közelítőleg ,,vízszintes síkok'' mentén állandó, pontosabb számolásnál a síkokat földsugárnyi sugarú gömbökkel kell helyettesíteni). A pontszerűnek tekinthető ,,sötét anyagdarabka'' gravitációs potenciálja is gömbfelületek mentén állandó, de ezen gömbök sugara sokkal kisebb, mint a Föld sugara. (Feltételezzük, hogy az égi jövevény megállt a tenger fenekén.) Az eredő gravitációs tér ekvipotenciális felületei a kérdéses helyen ,,kidudorodó'' felületek, a víz felszíne tehát a korábbi szinthez képest megemelkedik!
 
12. Legyen a kocka két szemközti lapja ABCD és A'B'C'D', a kocka élhosszát pedig válasszuk egységnek. A test öt csúcsa közül legalább három a kockának ugyanazon a lapján helyezkedik el. Az általánosság megszorítása nélkül feltehetjük, hogy ez a három csúcs az A, B és a C. A másik két csúcs elhelyezkedésétől függően több esetet kell megkülönböztetnünk.
Ha D is csúcsa a testnek, akkor A', B', C' vagy D' bármelyikét választjuk ötödiknek, egy négyzet alapú gúlát kapunk (1. ábra), melynek magassága a kocka élével egyenlő, tehát a térfogata 1⋅1⋅13, a kocka térfogatának harmada.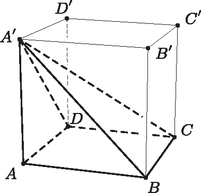
 

1. ábra

 


2. ábra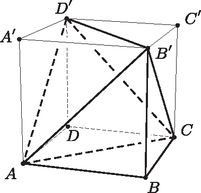

 

3. ábra

 


Ha D nincs a kiválasztott csúcsok közt, akkor A', B', C', D', közül kettőt választottunk. Ha D' nincs köztük, akkor vagy van olyan lap, amelynek mind a négy csúcsát kiválasztottuk, és így az előbb kapott négyzet alapú gúlához jutunk vagy az A', C' csúcsokat választottuk (2. ábra)). Ez a test egybevágó azzal a két másikkal, amelynek A' és D', illetve C' és D' a fedőlapon lévő csúcsai. Vizsgáljuk például az ABCA'C' testet (2. ábra). Az A, C, C', A' pontok egy síkban vannak, egy téglalap négy csúcsát alkotják, maga a test téglalap alapú gúla. Az ötödik csúcs távolsága az alaplaptól a kocka lapátlójának a felével egyenlő, ezért a gúla térfogata:
13(2⋅1⋅22)=13,
vagyis szintén a kocka térfogatának harmada.
Egy esetet kell még megvizsgálnunk, amikor A, B, C, D' és B' (3. ábra) a kiválasztott csúcsok. Ekkor a test két, az ACB' háromszöglap mentén összeillesztett tetraéderből áll. A BD' egyenes merőleges az ACB' háromszög síkjára, tehát a két tetraéder ACB' lapjához tartozó magasságának összege éppen BD'=3, a kocka testátlója.
 
Az ACB' háromszög mindhárom oldala lapátló, tehát területe (2)2⋅34=32.
 
A két tetraéder együttes térfogata így 13⋅32⋅3=12, azaz a kocka térfogatának fele.
Az öt csúcs által meghatározott test térfogata tehát a kocka térfogatának a fele vagy a harmada.
 
13. A II. Kepler-törvény érvényessége arra utal, hogy Furcsavilágban is centrális a Nap erőtere. A Nap (vonzócentrum) akkor lehet bolygók ellipszispályájának középpontjában, ha a bolygók mozgása két (eltérő amplitúdójú és különböző fázisú) harmonikus rezgőmozgásból tehető össze (szuperponálható). Az ilyen mozgás dinamikai feltétele: a vonzóerő nagysága egyenesen arányos a vonzócentrumtól mért távolsággal. Mivel a harmonikus rezgőmozgás periódusideje nem függ a rezgés amplitúdójától (az ellipszis méreteitől), a kérdéses hatványkitevő: n=0.
 
13+1. Legyen a feltételnek megfelelő módon megadott intervallumok jobb végpontjainak legkisebbike J1; hagyjuk el az intervallumok közül mindazokat ‐ a feltétel szerint legfeljebb hármat ‐, amelyek J1-et tartalmazzák. A megmaradó intervallumok egyike sem tartalmazza J1-et, rájuk a fenti eljárást megismételve a J2 végpontot kapjuk, és ismét legfeljebb három újabb intervallumot hagyhatunk el. További intervallumunk viszont már egyáltalán nem maradhat, hiszen egy ilyennek sem a J1, sem pedig a J2 végpontúval nem lehet közös pontja, e kettőnek pedig egymással szintén nincsen.
Azt kaptuk, hogy legfeljebb 6 intervallum adható meg az előírt módon. Ez viszont lehetséges is, ha közülük hármat-hármat ,,egymásba skatulyázunk''.
 
Megjegyzés. A megoldás során lényegében azt láttuk be, hogy ha intervallumok egy rendszerében bármely három között van két metsző, akkor létezik legfeljebb két pont ‐ ezek voltak J1 és J2 ‐ amelyek valamennyi intervallumot ,,lefogják'', azaz mindegyik intervallum tartalmaz a pontok közül legalább egyet.
Ez általában is igaz. Intervallumok bármely rendszerében az intervallumrendszert lefogó pontok számának a minimuma egyenlő a páronként közös pontok nélkül megadható intervallumok számának a maximumával. Ennél kevesebb pont nyilván nem elegendő valamennyi intervallum lefogásához, hiszen diszjunkt intervallumok lefogásához különböző pontokra van szükség. Az pedig, hogy ennyi ponttal megvalósítható valamennyi intervallum lefogása, éppen a megoldás gondolatmenetével igazolható, hiszen a kiválasztott J1,J2,...Jk végpontok egy diszjunkt intervallumrendszer végpontjai.
1A kérdések a 45. oldalon találhatók.