Kezdőlap


Cím:	A 44. Nemzetközi Fizikai Diákolimpiai feladatainak megoldása
Szerző(k):	Simon Péter , Tasnádi Tamás , Vigh Máté
Füzet:	2013/november, 489 - 503. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 44. Nemzetközi Fizikai Diákolimpia
feladatainak megoldása^{$^{*}$}

Elméleti feladatok

1. feladat. A Maribo-meteorit

A Maribo sebessége
1.1. A meteorit útját az 1. ábra mutatja. A

C

pont az észlelő biztonsági kamera helye,

M

a becsapódási pont,

F

a 155. képkockán,

G

pedig a 161. képkockán észlelt pozíció,

D

és

E

ezeknek a pontoknak a Föld felszínére vett vetülete. A

C B

egyenes észak‐déli irányban áll, az északi irányt a nyíl jelzi.

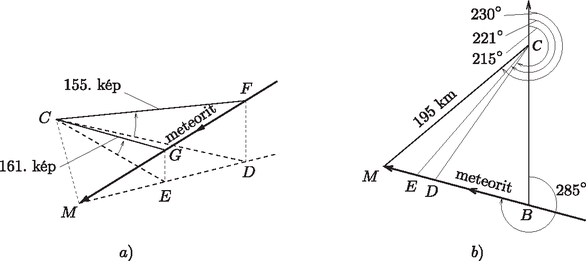1. ábra. A meteorit pályája a légkörben.

a)

Elforgatott, távlati nézet (nem méretarányos).

b)

Vízszintes síkra vett vetület

A megadott szögeket az

1. b)

vetületi rajzon ívek jelölik. Ezekből megkapható az ábrán az összes többi szög is, és az

| M C | = 195 km

oldal ismeretében, elemi geometriai úton (a szinusz-tétel alkalmazásával) megkaphatóak a következő oldalak:

\begin{matrix} | C D | = 170, 0 km, |CE| = 177,7 km, |DE| =19,77km. \end{matrix}

1. a)

távlati rajzon az ívvel jelölt, ismert magassági szögek segítségével az

F

és

G

pont magassága megkapható:

\begin{matrix} | D F | = | C D | \cdot tg (19, 2^{\circ}) = 59, 20 km, |EG| = |CE|\cdottg(14,7^{\circ}) =46,62 km. \end{matrix}

Ezután a 155. és a 161. képkocka között megtett

| F G |

út Pitagorasz tételéből adódik:

\begin{matrix} | F G | = \sqrt[]{{| D E |}^{2} + {(| D F | - | E G |)}^{2}} = 23, 43 km, \end{matrix}

így a képkockák idejének ismeretében a keresett sebesség:

\begin{matrix} v = \frac{| F G |}{2, 28 s -1,46 s} = 28, 6 \frac{km}{s} . \end{matrix}

Megolvad-e a meteorit az atmoszférában?
1.2a. A légkörben lassuló meteoroidra sebességtől függő, változó erő hat, így mozgását az

\begin{matrix} m_{M} \frac{d v}{d t} = - λ v^{2}, λ = k ϱ_{atm} π R_{M}^{2} \end{matrix}

differenciálegyenlet írja le, mely a változók szétválasztásának módszerével egzaktul megoldható:

\begin{matrix} \frac{d v}{v^{2}} = - \frac{λ}{m_{M}} d t, \int_{v_{M}}^{0, 9 v_{M}} \frac{d v}{v^{2}} = - \int_{0}^{t_{1}} \frac{λ}{m_{M}} d t, - (\frac{1}{0, 9} - 1) \frac{1}{v_{M}} = - \frac{λ}{m_{M}} t_{1} . \end{matrix}

Így a keresett idő:

\begin{matrix} t_{1} = \frac{m_{M}}{k ϱ_{atm} π R_{M}^{2}} (\frac{1}{0, 9} - 1) \frac{1}{v_{M}} = 0, 88 s . \end{matrix}

Differenciálegyenlet nélkül is adható egy igen jó közelítő megoldás. Miközben a sebesség

v_{M}

-ről

0, 9 v_{M}

-re csökken, a közegellenállási erő nem nagyon változik, átlagos értékét vehetjük

F_{átl} = - λ {(0, 95 v_{M})}^{2}

-nek. Ebből a mozgás átlagos lassulása

a_{átl} = \frac{F_{átl}}{m_{M}}

, ahonnan a keresett idő:

\begin{matrix} t_{1} = \frac{- 0, 1 v_{M}}{a_{átl}} = \frac{m_{M}}{k ϱ_{atm} π R_{M}^{2}} \frac{0, 1}{{(0, 95)}^{2}} \frac{1}{v_{M}} = 0, 87 s . \end{matrix}

1.2b. A meteoroid kinetikus energiájának és a teljes megolvasztáshoz szükséges energiának a hányadosa ismert összefüggések alapján:

\begin{matrix} \frac{E_{kin}}{E_{olv}} = \frac{\frac{1}{2} m_{M} v_{M}^{2}}{c_{kő} m_{kő} (T_{kő} - T_{0}) + m_{kő} L_{kő}} = 2, 1 \cdot 10^{2} ≫ 1. \end{matrix}

A Maribo melegedése a légkörön való áthatolás alatt
1.3a. Az

x \approx t^{α} ϱ_{kő}^{β} c_{kő}^{γ} k_{kő}^{δ}

összefüggésben csak a dimenziókat megtartva az

\begin{matrix} 1 m = {(1 s)}^{α} \cdot {(1 \frac{kg}{m^{3}})}^{β} \cdot {(1 \frac{m^{2}}{s^{2} K})}^{γ} \cdot {(1 \frac{kg  m}{s^{3} K})}^{δ} \end{matrix}

egyenletet kapjuk, ami a keresett kitevőkre a

\begin{matrix} β + δ = 0, - 3 β + 2 γ + δ = 1, α - 2 γ - 3 δ = 0, - γ - δ = 0 \end{matrix}

lineáris egyenletrendszert adja. Ennek megoldása

\begin{matrix} α = δ = \frac{1}{2}, β = γ = - \frac{1}{2}, tehát x \approx \sqrt[]{\frac{k_{kő} t}{ϱ_{kő} c_{kő}}} . \end{matrix}

1.3b. A kapott képletbe beírva az adatokat,

\begin{matrix} x (5 s) = 1, 6 mm és \frac{x}{R_{M}} = \frac{1, 6 mm}{130 mm} = 0, 012. \end{matrix}

A meteorit kora
1.4a. Mivel a

_{37}^{87} Rb

izotóp

_{38}^{87} Sr

-ra való bomlásakor a tömegszám nem változik, a rendszám eggyel nő, negatív béta-bomlásról van szó, melynek egyenlete:

\begin{matrix} _{37}^{87} Rb \to_{38}^{87} Sr + e^{-} + {\bar{ν}}_{e} . \end{matrix}

1.4b. A

^{87} Rb

izotópok száma a bomlás miatt exponenciálisan csökken az idő függvényében, ugyanakkor a

^{87} Sr

izotópok száma az elbomlott

^{87} Rb

izotópok számával nő, tehát:

\begin{matrix} N_{87 Rb} (t) & = N_{87 Rb} (0) e^{- λ t}, \\ N_{87 Sr} (t) & = N_{87 Sr} (0) + (N_{87 Rb} (0) - N_{87 Rb} (t)) = N_{87 Sr} (0) + (e^{λ t} - 1) N_{87 Rb} (t) . \end{matrix}

A második egyenletet elosztva a

^{86} Sr

izotópok számával, megkapjuk az egyidejűségi egyenes egyenletét

\begin{matrix} \frac{N_{87 Sr} (t)}{N_{86 Sr}} = \frac{N_{87 Sr} (0)}{N_{86 Sr}} + (e^{λ t} - 1) \frac{N_{87 Rb} (t)}{N_{86 Sr}}, \end{matrix}

melynek meredeksége valóban

e^{λ t} - 1

.
1.4c.

A grafikonról leolvasható, hogy a meredekség

a = e^{λ t} - 1 = \frac{0, 712 - 0, 700}{0, 25} = 0, 050

. A felezési idő és a bomlási állandó

kapcsolata:

T_{1 / 2} = \frac{ln 2}{λ} = 4, 9 \cdot 10^{10}

év. Így a meteorit életkora:

\begin{matrix} τ_{M} = \frac{ln (1 + a)}{λ} = \frac{ln (1 + a)}{ln 2} T_{1 / 2} = 3, 4 \cdot 10^{9} év . \end{matrix}

Az Encke-üstökös, ahonnan a Maribo-meteorit származhat
A Nap körül keringő Encke-üstökös Naptól mért legkisebb és legnagyobb távolsága:

\begin{matrix} a_{min} = 4, 95 \cdot 10^{10} m és a_{max} = 6, 16 \cdot 10^{11} m . \end{matrix}

1.5. Az Encke üstökös pályájának fél nagytengelye

a_{Encke} = \frac{1}{2} (a_{min} + a_{max}) = 3, 33 \cdot 10^{11} m

. Kepler III. törvényét alkalmazva a Földre és az Encke üstökösre azt kapjuk, hogy:

\begin{matrix} \frac{a_{Encke}^{3}}{t_{Encke}^{2}} = \frac{a_{N-F}^{3}}{t_{Föld}^{2}}, tehát t_{Encke} = \sqrt[]{\frac{a_{Encke}^{3}}{a_{N-F}^{3}}} \cdot t_{Föld} = 3, 30 év = 1, 04 \cdot 10^{8} s . \end{matrix}

Aszteroida-becsapódás hatása a Földre
1.6a. A Föld tehetetlenségi nyomatékát (a forgástengely irányában) elhanyagolhatóan befolyásolja az aszteroida becsapódása, hiszen a becsapódás helye a forgástengelyre esik. Tehát a Föld impulzusmomentumának és a forgástengelyének iránya az ütközés előtt és után is egybeesik. Ezért a forgástengely szögeltérülése helyett a Föld impulzusmomentum-vektorának maximális szögeltérülését határozzuk meg az impulzusmomentum megmaradását felhasználva.
A Föld saját impulzusmomentuma a megadott adatok alapján ismert:

\begin{matrix} N_{F} = Θ_{F} ω_{F} = 0, 83 \frac{2}{5} m_{F} R_{F}^{2} \frac{2 π}{24 h} = 5, 87 \cdot 10^{33} \frac{kg m^{2}}{s} . \end{matrix}

Az Északi sarkra becsapódó aszteroidának a Föld középpontjára vonatkoztatott impulzusmomentuma akkor maximális, ha az aszteroida a Föld forgástengelyére merőlegesen mozog, tehát a felszínre érintőlegesen csapódik be. Ekkor az aszteroida impulzusmomentuma:

N_{aszt} = m_{aszt} v_{aszt} R_{F} = 2, 51 \cdot 10^{26} \frac{{kg m}^{2}}{s}

.
Ütközéskor a Föld impulzusmomentuma az aszteroida impulzusmomentumával változik, ezért a Föld impulzusmomentum-vektorának szögeltérülése akkor a legnagyobb, ha az aszteroida impulzusmomentuma merőleges a Földére. Érintőleges becsapódáskor ez a feltétel is teljesül. Így az impulzusmomentum (és egyben a forgástengely) maximális szögeltérülése:

\begin{matrix} Δ φ \approx tg (Δ ϕ) = \frac{N_{aszt}}{N_{F}} = 4, 27 \cdot 10^{- 8} rad . \end{matrix}

Megjegyezzük, hogy a forgástengelynek a Föld felszínével való metszéspontja

R_{F} Δ φ = 27 cm

-rel mozdul el. Azt is érdemes látni, hogy ez az elmozdulás merőleges az aszteroida becsapódási sebességére, hiszen az aszteroida impulzusmomentumának irányába esik.
1.6b. Az Egyenlítőre való függőleges becsapódáskor nem változik a Föld impulzusmomentuma, hiszen az aszteroida impulzusmomentuma a Föld középpontjára vonatkoztatva zérus. Azonban

Δ Θ_{F} = m_{aszt} R_{F}^{2}

-tel megnő a Föld tehetetlenségi nyomatéka, és ez okozza a szögsebesség lassulását:

\begin{matrix} Θ_{F} ω_{F} = (Θ_{F} + Δ Θ_{F}) (ω_{F} + Δ ω_{F}), Δ ω_{F} & \approx - \frac{Δ Θ_{F} ω_{F}}{Θ_{F}} = - 5, 76 \cdot 10^{- 14} \frac{1}{s} . \end{matrix}

Így a Föld forgási periódusának növekedése:

\begin{matrix} Δ T_{F} = 2 π (\frac{1}{ω_{F} + Δ ω_{F}} - \frac{1}{ω_{F}}) \approx - 2 π \frac{Δ ω_{F}}{ω_{F}^{2}} = 6, 84 \cdot 10^{- 5} s . \end{matrix}

1.6c. Ebben az esetben az aszteroida és a Föld impulzusmomentuma egy egyenesbe esik, és becsapódáskor a Föld impulzusmomentuma és tehetetlenségi nyomatéka is megváltozik. A teljes rendszer impulzusmomentuma megmarad, tehát

\begin{matrix} N_{F} \pm N_{aszt} = (Θ_{F} + Δ Θ_{F}) (ω_{F} + Δ ω_{F}), \\ Δ ω_{F} \approx \frac{- Δ Θ_{F} ω_{F} \pm N_{aszt}}{Θ_{F}} \approx \pm \frac{N_{aszt}}{Θ_{F}} = \pm 3, 11 \cdot 10^{- 12} \frac{1}{s} . \end{matrix}

(Felhasználtuk, hogy

\frac{Δ Θ_{F} ω_{F}}{N_{aszt}} \approx 5 \cdot 10^{- 16} ≪ 1

. A

\pm

előjel azt veszi számításba, hogy az aszteroida impulzusmomentuma azonos vagy ellentétes irányú a Földével.) Innen a Föld forgási periódusának megváltozása:

\begin{matrix} Δ T_{F} \approx - 2 π \frac{Δ ω_{F}}{ω_{F}^{2}} = \mp 3, 62 \cdot 10^{- 3} s . \end{matrix}

Maximális becsapódási sebesség
1.7. A maximális becsapódási sebességet három lépésben határozzuk meg.
Az energiamegmaradás törvénye szerint a Nap gravitációs terében a Naptól a Föld pályasugarával megegyező távolságban az

m

tömegű test maximális

v_{1}

sebességére

\begin{matrix} 0 = \frac{1}{2} m v_{1}^{2} - G \frac{m m_{N}}{a_{N-F}} teljesül,  ahonnan v_{1} = \sqrt[]{\frac{2 G m_{N}}{a_{N-F}}} = 42, 1 \frac{km}{s} . \end{matrix}

Szerencsés esetben a test éppen szembe halad

a pályáján

v_{F} = \frac{2 π a_{N-F}}{1 év} = 29, 8 \frac{km}{s}

sebességgel keringő Földdel, tehát a Föld vonatkoztatási rendszerében a sebessége

v_{1} + v_{F}

.
Most a Föld vonatkoztatási rendszerében írhatjuk föl az energiamegmaradás törvényét:

\begin{matrix} \frac{1}{2} m {(v_{1} + v_{F})}^{2} = \frac{1}{2} m {(v_{becs}^{max})}^{2} - G \frac{m m_{F}}{R_{F}} . \end{matrix}

(A Nap hatását elhanyagolhatjuk, hiszen a Föld közelében a Nap gravitációs potenciálja közel állandó.) Innen a becsapódás maximális sebessége:

\begin{matrix} v_{becs}^{max} = \sqrt[]{{(v_{1} + v_{F})}^{2} + \frac{2 G m_{F}}{R_{F}}} = 72, 8 \frac{km}{s} . \end{matrix}

2. feladat. Plazmonos gőzfejlesztő készülék

2.1. Az ezüst nanogolyócska térfogata:

V = \frac{4 π}{3} R^{3} = 4, 19 \cdot 10^{- 24} m^{3}

, tömege:

M = ϱ_{Ag} V = 4, 39 \cdot 10^{- 20} kg

; a nanogolyócskában található ezüstionok száma:

N = N_{A} \frac{M}{M_{Ag}} = 2, 45 \cdot 10^{5}

; töltéssűrűsége:

ϱ = e N / V = 9, 38 \cdot 10^{9} {Cm}^{- 3}

; a szabad elektronok koncentrációja:

n = N / V = 5, 85 \cdot 10^{28} m^{- 3}

, összes töltése:

Q = - e N = - 3, 93 \cdot 10^{- 14} C

; a töltéshordozók összes tömege:

m_{0} = m_{e} N = 2, 23 \cdot 10^{- 25} kg

2.2. Egy

R

sugarú, homogén töltéseloszlású, pozitív

ϱ

töltéssűrűségű gömb középpontjától

| r | < R

távolságban lévő pontban az elektromos térerősség nagysága a Gauss-törvényből kapható meg:

\begin{matrix} E_{+} (r) 4 π r^{2} = \frac{4 π}{3} r^{3} \frac{ϱ}{ε_{0}}, \end{matrix}

a térerősség irányát is figyelembe véve:

\begin{matrix} E_{+} = \frac{ϱ}{3 ε_{0}} r . \end{matrix}

Hasonlóan számolható az

R_{1}

sugarú,

- ϱ

töltéssűrűségű gömb tere a gömbön belül, annak középpontjától

| r' | = | r - x_{d} |

távolságban:

E_{-} = - \frac{ϱ}{3 ε_{0}} (r - x_{d})

. Az

R_{1}

sugarú gömbön belül az eredő elektromos térerősség tehát:

\begin{matrix} E = E_{+} + E_{-} = \frac{ϱ}{3 ε_{0}} x_{d}, \end{matrix}

a keresett együttható értéke tehát

A = 1 / 3

2.3. Az előző részfeladat eredménye szerint az elektromos tér a töltéssemleges tartományban

E = (ϱ / (3 ε_{0})) x_{d}

értékű, így az ebben a térrészben elhelyezkedő, közelítőleg

Q

össztöltésű elektronfelhőre ható erő:

\begin{matrix} F = Q E = - e N \frac{ϱ}{3 ε_{0}} x_{d} = - \frac{4 π}{9 ε_{0}} R^{3} e^{2} n^{2} x_{d} . \end{matrix}

Az elektronfelhő elmozdítása során ennek az erőnek a

(- 1)

-szeresét kell kifejtenünk. Mivel a szükséges erő nagysága az elmozdulással egyenesen arányos, ezért számolhatunk úgy, mintha végig a maximális erő felével történt volna a munkavégzés:

\begin{matrix} W_{el} = \frac{1}{2} | F_{max} | x_{d} = \frac{2 π}{9 ε_{0}} R^{3} e^{2} n^{2} x_{d}^{2} . \end{matrix}

2.4. Az ezüstgolyócska belsejében az eredő elektromos térnek zérusnak kell lennie, így az elmozdított töltések által a töltéssemleges térrészben keltett térerősség

- E_{0} = E_{0} e_{x}

. A 2.2. rész eredményét felhasználva kifejezhető az elektronfelhő

x_{p}

elmozdulása:

\begin{matrix} x_{p} = \frac{3 ε_{0}}{ϱ} E_{0} = \frac{3 ε_{0}}{e n} E_{0} . \end{matrix}

A kicsiny

x_{p}

elmozdulás közben a golyócska közepén átmenő

(y, z)

síkon közelítőleg egy

π R^{2} x_{p}

térfogatú hengerben található elektronok haladnak át. Ezek (negatív) össztöltése:

- Δ Q = - π R^{2} x_{p} ϱ = - π R^{2} e n x_{p}

2.5a. Feleltessük meg a töltések széthúzásakor végzett

W_{el}

munkát a kondenzátor energiájának, a szétválasztott

Δ Q

töltést pedig a kondenzátor töltésének! A

W_{el} = Δ Q^{2} / (2 C)

összefüggést használva a nanogolyócskát helyettesítő kondenzátor kapacitása:

\begin{matrix} C = \frac{Δ Q^{2}}{2 W_{el}} = \frac{9 π}{4} ε_{0} R = 6, 26 \cdot 10^{- 19} F . \end{matrix}

2.5b. A kondenzátorra vonatkozó

V_{0} = Δ Q / C

összefüggést és az eddigi eredményeket felhasználva:

\begin{matrix} V_{0} = \frac{Δ Q}{C} = \frac{π R^{2} e n x_{p}}{\frac{9 π}{4} ε_{0} R} = \frac{4}{3} R (\frac{e n x_{p}}{3 ε_{0}}) = \frac{4}{3} R E_{0} . \end{matrix}

2.6a. Az elektronfelhőben található

N

darab elektron összes mozgási energiája:

\begin{matrix} W_{kin} = \frac{1}{2} m_{e} v^{2} N = \frac{2 π}{3} R^{3} n m_{e} v^{2} . \end{matrix}

I

áramerősség nagysága megkapható, ha elosztjuk a

π R^{2}

alapterületű,

v Δ t

magasságú hengerben található elektronok össztöltését a

Δ t

időtartammal:

\begin{matrix} I = π R^{2} e n v . \end{matrix}

2.6b. A mozgó elektronok

W_{kin}

kinetikus energiája megfeleltethető egy

L

induktivitású,

I

árammal átjárt vezető

L I^{2} / 2

energiájával, ebből:

\begin{matrix} L = \frac{2 W_{kin}}{I^{2}} = \frac{4 m_{e}}{3 π R n e^{2}} = 2, 57 \cdot 10^{- 14} H . \end{matrix}

2.7a. A helyettesítő áramkör

C

kapacitásából és

L

induktivitásából a rezonanciafrekvencia kiszámítható:

\begin{matrix} ω_{p} = \frac{1}{\sqrt[]{L C}} = \sqrt[]{\frac{n e^{2}}{3 m_{e} ε_{0}}} . \end{matrix}

2.7b. Behelyettesítve

ω_{p} = 7, 88 \cdot 10^{15} rad/s

adódik, a hullámhosszra pedig

λ_{p} = 2 π c / ω_{p} = 239 nm

-t kapunk.

2.8a. Egyetlen elektron időátlagolt kinetikus energiája

\frac{1}{2} m_{e} 〈 v^{2} 〉

. Mivel az ütközések egy-egy elektronnál

τ

időnként történnek, és összesen

N

darab elektronunk van, az energiadisszipáció teljesítménye:

\begin{matrix} P_{hő} = \frac{1}{2 τ} N m_{e} 〈 v^{2} 〉 = \frac{2 π}{3 τ} R^{3} n m_{e} 〈 v^{2} 〉 . \end{matrix}

Az áramerősség négyzetének időátlagát a 2.6a. részben kapott eredményből származtathatjuk:

\begin{matrix} 〈 I^{2} 〉 = {(π R^{2} e n)}^{2} 〈 v^{2} 〉 . \end{matrix}

2.8b. A Joule-hőre vonatkozó

P_{hő} = R_{hő} 〈 I^{2} 〉

összefüggést használva:

\begin{matrix} R_{hő} = \frac{2 m_{e}}{3 π n e^{2} R τ} = 2, 46 Ω . \end{matrix}

2.9. Az előző részhez hasonlóan induljunk ki a

P_{szórt} = R_{szórt} 〈 I^{2} 〉

összefüggésből!

\begin{matrix} R_{szórt} = \frac{P_{szórt}}{〈 I^{2} 〉} = \frac{Q^{2} x_{0}^{2} ω_{p}^{4}}{12 π ε_{0} c^{3} {(π R^{2} e n)}^{2} 〈 v^{2} 〉} . \end{matrix}

Használjuk fel, hogy

v (t) = - x_{0} ω_{p} sin (ω_{p} t)

, így

〈 v^{2} 〉 = x_{0}^{2} ω_{p}^{2} / 2

, valamint, hogy

Q = (4 π / 3) R^{3} e n

. Behelyettesítve, egyszerűsítés után kapjuk:

\begin{matrix} R_{szórt} = \frac{8}{27} \frac{R^{2} ω_{p}^{2}}{π ε_{0} c^{3}} = 2, 45 Ω . \end{matrix}

2.10a. A nanogolyócskát gerjesztő fény frekvenciája éppen megegyezik a rezgő elektronfelhő rezonanciafrekvenciájával, ezért a helyettesítő áramkör eredő impedanciája tisztán ohmikus,

R_{hő} + R_{szórt}

értékű. A helyettesítő feszültségforrás feszültségének amplitúdója 2.5b. alapján

V_{0} = 4 R E_{0} / 3

, effektív értéke pedig a szinuszos változás miatt

V_{0} / \sqrt[]{2}

. A két fogyasztó között az ellenállások arányában oszlik meg a feszültség, így az időátlagolt teljesítmények a következőképp számolhatók:

\begin{matrix} P_{hő} & = & \frac{(\frac{R_{hő}}{R_{hő} + R_{szórt}} \frac{V_{0}}{\sqrt[]{2}})^{2}}{R_{hő}} = \frac{8 R_{hő} R^{2}}{9 {(R_{hő} + R_{szórt})}^{2}} E_{0}^{2}, \\ P_{szórt} & = & \frac{R_{szórt}}{R_{hő}} P_{hő} = \frac{8 R_{szórt} R^{2}}{9 {(R_{hő} + R_{szórt})}^{2}} E_{0}^{2} . \end{matrix}

A beeső fény amplitúdóját a Poynting-vektor nagyságából kaphatjuk meg:

\begin{matrix} E_{0} = \sqrt[]{\frac{2 S}{ε_{0} c}} . \end{matrix}

2.10b. A megadott adatokat a 2.10a. részben kapott kifejezésekbe helyettesítve a

P_{hő} = 6, 82 nW

P_{szórt} = 6, 81 nW

és

E_{0} = 27, 4 kV/m

eredményeket kapjuk.

2.11a. A tartályban lévő nanogolyócskák száma

N_{ng} = a h^{2} n_{ng} = 7, 3 \cdot 10^{11}

, a teljes fejlődő Joule-hő tehát

P_{gőz} = N_{ng} P_{hő} = 4, 98 kW

. Ez a teljesítmény a víz felmelegítésére, elforralására és a gőz felmelegítésére fordítódik:

\begin{matrix} P_{gőz} = m_{gőz} (c_{víz} (T_{100} - T_{hő}) + L_{víz} + c_{gőz} (T_{gőz} - T_{100})), \end{matrix}

ebből az időegység alatt képződő vízgőz tömege:

\begin{matrix} m_{gőz} = \frac{P_{gőz}}{c_{víz} (T_{100} - T_{hő}) + L_{víz} + c_{gőz} (T_{gőz} - T_{100})} = 1, 90 \cdot 10^{- 3} kg/s. \end{matrix}

2.11b. A beeső fény teljes teljesítménye

h^{2} S = 10, 0 kW

, ebből csak a gőzképződésre fordítódó

P_{gőz} = 4, 98 kW

a hasznos teljesítmény, így a gőzfejlesztő készülék hatásfoka

η = 4, 98 kW / 10, 0 kW = 0, 498

3. feladat. A grönlandi jégsapka

3.1. A jégtakaró belsejében a hidrosztatikai nyomás, mint a jégválasztó vonaltól mért

x

távolság és a földfelszíntől (tengerszinttől) mért

z

magasság függvénye:

p (x, z) = ϱ_{jég} g (H (x) - z)

3.2a. Az

y

‐

z

síktól (,,jégválasztótól'')

x

távolságra lévő függőleges oldalfalra ható erő kifejezhető:

\begin{matrix} F (x) = Δ y \int_{0}^{H (x)} ϱ_{jég} g (H (x) - z) d z=\frac{1}{2}Δyϱ_{jég}g H{(x)}^{2}. \end{matrix}

A függőleges oldalfalú jégrétegre ható két vízszintes erő különbsége:

\begin{matrix} Δ F = F (x) - F (x + Δ x) = - \frac{dF}{dx} Δ x = - Δ y ϱ_{jég} g H (x) \frac{d H}{dx} Δ x . \end{matrix}

Használjuk fel, hogy

Δ F = S_{b} Δ x Δ y

. Így adódik

S_{b}

értékére:

\begin{matrix} S_{b} = \frac{Δ F}{Δ x Δ y} = - ϱ_{jég} g H (x) \frac{d H}{dx} . \end{matrix}

Ezzel igazoltuk, hogy

S_{b} = k H (x) d H/ dx

, ahol az arányossági tényező

k = - ϱ_{jég} g

3.2b. Megkapjuk a jégsapka

H (x)

magasságprofilját, ha megoldjuk a következő differenciálegyenletet:

\begin{matrix} S_{b} = - ϱ_{jég} g H (x) \frac{d H}{dx}, ebből H dH=-\frac{S_{b}}{ϱ_{jég} g} dx. \end{matrix}

Integráljuk mindkét oldalt:

\begin{matrix} H {(x)}^{2} = - \frac{2 S_{b}}{ϱ_{jég} g} x + C . \end{matrix}

Használjuk fel, hogy

H

értéke az

x = L

helyen 0. Így az integrációs állandóra adódik:

\begin{matrix} C = \frac{2 S_{b}}{ϱ_{jég} g} L . \end{matrix}

Most már a

H (x)

magasságprofil megadható:

\begin{matrix} H (x) = \sqrt[]{\frac{2 S_{b}}{ϱ_{jég} g} (L - x)} . \end{matrix}

Megadhatjuk

H

legnagyobb értékét, melyet az

x = 0

helyen vesz fel a függvény:

\begin{matrix} H_{m} = \sqrt[]{\frac{2 S_{b}}{ϱ_{jég} g} L} . \end{matrix}

3.2c. Grönland modelljében a jégsapka alapja egy téglalap, amelynek területe

A = 10 L^{2}

. A jégsapka térfogatát úgy fogjuk megkapni, ha a 3.2b. feladatrészben megismert magasságprofilt erre a területre integráljuk.

\begin{matrix} V_{jég} & = (5 L) 2 \int_{0}^{L} H (x) dx=10L\int_{0}^{L}{(\frac{2 S_{b}}{ϱ_{jég} g})}^{\frac{1}{2}}\sqrt[]{L - x} dx== 10LH_{m}\int_{0}^{L}\sqrt[]{1 - \frac{x}{L}} dx . \end{matrix}

Áttérve az

u = 1 - x / L

integrálási változóra:

\begin{matrix} V_{jég} = 10 L^{2} H_{m} \int_{0}^{1} \sqrt[]{u} du =10L^{2}H_{m}\cdot\frac{2}{3}. \end{matrix}

Felhasználva, hogy

H_{m} \propto L^{1 / 2}

, illetve az

L \propto A^{1 / 2}

arányosságot azt kapjuk, hogy

V_{jég} \propto A^{5 / 4}

. Tehát a keresett kitevő

γ = 5 / 4

3.3. A szimmetria miatt a jégválasztónál a jég

x

-irányú sebessége 0, tehát

v_{x} (x = 0) = 0

. Tekintsük a jégsapka

x = 0

és

x > 0

között elhelyezkedő,

Δ y

szélességű darabját! Erre a darabra a hóesések miatt egységnyi idő alatt

V_{be} = c x Δ y

térfogatú jég rakódik. Eközben a kiszemelt jégdarab

x > 0

-nál elhelyezkedő,

H_{m} Δ y

területű, függőleges keresztmetszetén egységnyi idő alatt

V_{ki} = v_{x} (x) H_{m} Δ y

térfogatú jég áramlik ki. Mivel a jégsapka alakja időben állandósult állapotban található,

V_{be} = V_{ki}

, ahonnan a

\begin{matrix} v_{x} (x) = \frac{c x}{H_{m}} \end{matrix}

eredményt kapjuk.

3.4. A jég áramlási sebességének komponenseire vonatkozó

d v_{x} / d x + d v_{z} / d z = 0

egyenletből, valamint a 3.3. feladatrész eredményét használva:

\begin{matrix} \frac{d v_{z}}{d z} = - \frac{c}{H_{m}} . \end{matrix}

Integrálás után:

\begin{matrix} v_{z} (z) = - \frac{c z}{H_{m}} + C, \end{matrix}

ahol a

C

integrálási változó a

v_{z} (z = 0) = 0

feltétel miatt zérus. A jégdarabkák függőleges sebességkomponense tehát:

\begin{matrix} v_{z} (z) = - \frac{c z}{H_{m}} . \end{matrix}

3.5. A jégdarabka sebességének

x

- és

z

-irányú komponensére kapott kifejezések differenciálegyenleteket szolgáltatnak az

x (t)

z (t)

koordinátákra:

\begin{matrix} \frac{d x}{d t} = \frac{c}{H_{m}} x, \frac{d z}{d t} = - \frac{c}{H_{m}} z . \end{matrix}

A kezdeti feltételeket (

z (0) = H_{m}, x (0) = x_{i}

) figyelembe véve a következő két függvény adódik eredményül:

\begin{matrix} x (t) = x_{i} e^{\frac{c}{H_{m}} t}, z (t) = H_{m} e^{- \frac{c}{H_{m}} t} . \end{matrix}

A két függvényt összeszorozva az idő kiküszöbölhető:

x \cdot z = x_{i} H_{m}

, amiből látható, hogy a jégdarabka pályája egy

\begin{matrix} x = \frac{x_{i} H_{m}}{z} \end{matrix}

egyenletű hiperbola.

3.6. A jégválasztónál (

x = 0

) az áramlás csak függőleges irányú, és a

z (t)

függvényt a 3.5. feladatrészben már felírtuk. Képezzük ennek inverzét:

\begin{matrix} τ (z) = \frac{H_{m}}{c} ln (\frac{H_{m}}{z}) . \end{matrix}

3.7a. A

c_{ig}

jégképződési sebesség meghatározásához szükségünk van a következő adatokra:

T_{1} = 11700

év;

z_{1} = 3060 m - 1492 m = 1568

H_{m} = 3060

m. A 3.6. feladatrészben levezetett függvényt használva:

\begin{matrix} c_{ig} = \frac{H_{m}}{T_{1}} ln (\frac{H_{m}}{z_{1}}) = 0, 175 m/év . \end{matrix}

A jégkorszak 120 ezer évvel ezelőtti kezdete a feladat szövege szerint 3040 m mélységnek feleltethető meg. Használjuk a jégfolyam áramlási sebességének függőleges komponensére a 3.4. feladatrészben kapott összefüggést:

\begin{matrix} \frac{d z}{d t} = - \frac{c}{H_{m}} z . \end{matrix}

Átrendezve, majd mindkét oldalt integrálva 3040 m mélységtől a felszínig:

\begin{matrix} H_{m} (- \frac{1}{z}) d z & = & c d t, \\ H_{m} ln (\frac{H_{m}}{H_{m} - 3040}) & = & \int_{11 700 év}^{120 000 év} c_{jk} d t + \int_{0}^{11 700 év} c_{ig} d t, \\ H_{m} ln (\frac{H_{m}}{H_{m} - 3040}) & = & c_{jk} \cdot (108 300 év) + c_{ig} \cdot (11 700 év) . \end{matrix}

Az egyenlet rendezése és behelyettesítés után a

c_{jk} = 0, 123

m/év eredményt kapjuk, ami sokkal kevesebb csapadékot jelent, mint napjainkban.

3.7b. A feladat szövegében (lásd a KöMaL múlt havi számát) az 5. ábra

(b)

grafikonjáról leolvasható, hogy a jégkorszakból a jégkorszak utáni időszakba történő átmenetkor a

δ^{18}

O értéke kb.

- 43

ezrelékről

- 34

ezrelékre változott. Az 5. ábra

(a)

grafikonja szerint

δ^{18}

O értékének ilyen változása kb.

- 40^{\circ}

C és

- 30^{\circ}

C hőmérsékletek között következik be, ez

10^{\circ}

C hőmérsékletemelkedést jelent.

3.8. A jégsapka alapját modellező téglalap területét ismerve kiszámolható a téglalap

L

hosszúságparamétere:

\begin{matrix} L = \sqrt[]{A_{G} / 10} = 4, 14 \cdot 10^{5} m . \end{matrix}

A jégsapka térfogatának kiszámításához használjuk a 3.2b. és 3.2c. részben kapott eredményeket!

\begin{matrix} V_{jég} = \frac{20}{3} L^{2} H_{m} = \frac{20}{3} L^{5 / 2} \sqrt[]{\frac{2 S_{b}}{ϱ_{jég} g}} = 3, 46 \cdot 10^{15} m^{3} . \end{matrix}

Ennek a jégnek a megolvadása során keletkező víz térfogata:

\begin{matrix} V_{víz} = \frac{ϱ_{jég}}{ϱ_{víz}} V_{jég} = 3, 18 \cdot 10^{15} m^{3}, \end{matrix}

ezt az eredményt elosztva a Föld óceánjainak teljes területével megkapjuk az olvadás okozta átlagos vízszintemelkedést:

\begin{matrix} h = \frac{V_{víz}}{A_{óceán}} = 8, 82 m . \end{matrix}

3.9. Az óceán felszíne ekvipotenciális. A vízfelszín

h

magasságban lévő, Grönlandtól

r

távolságra elhelyezkedő,

m

tömegű darabkájának potenciális energiája egyrészt a Föld gravitációs terétől (

m g h

), másrészt Grönland gravitációs vonzásából

(- G \frac{m_{jég} m}{r})

származik:

\begin{matrix} U = m g h - G \frac{m_{jég} m}{r}, \end{matrix}

ebből kifejezve a vízszint

h

magasságát:

\begin{matrix} h = h_{0} + \frac{G m_{jég}}{g r}, \end{matrix}

ahol bevezettük a

h_{0} = U / m g

jelölést. A 2. ábrán látható

ϑ

középponti szöggel az

r

távolság kifejezhető, ennek segítségével megkapható a vízmagasság

θ

-függése:

\begin{matrix} h (ϑ) = h_{0} + \frac{G m_{jég}}{2 g R_{F} | sin (ϑ / 2) |} . \end{matrix}

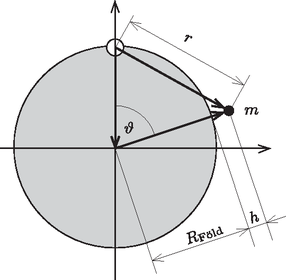2. ábra.

Az ismert adatokat és a Grönlandon található jég tömegét (

m_{jég} = ϱ_{jég} V_{jég} = 3, 18 \cdot 10^{18} kg

) behelyettesítve:

\begin{matrix} h (ϑ) = h_{0} + \frac{1, 69 m}{| sin (ϑ / 2) |} . \end{matrix}

A Grönland és Koppenhága között lévő körívhez tartozó

ϑ

középponti szög:

\begin{matrix} ϑ = \frac{3500 km}{R_{F}} = 31, 4^{\circ}, \end{matrix}

Grönland és a tőle legtávolabbi földrajzi pont közötti középponti szög pedig

180^{\circ}

, ezzel a keresett vízszintkülönbség:

\begin{matrix} h_{CPH} - h_{OPP} = h_{0} + \frac{1, 69 m}{| sin (31, 4^{\circ} / 2) |} - (h_{0} + \frac{1, 69 m}{| sin (180^{\circ} / 2) |}) = 4, 56 m . \end{matrix}

Kísérleti feladatok

1. feladat. Fénysebesség és törésmutató mérése lézeres távolságmérővel

Ebben a feladatban a versenyzők egy barkácsboltokban is kapható, Bosch márkájú lézeres távolságmérővel (LTM) végezhettek méréseket. Az LTM egy adóból és egy vevőből áll. Az adó egy félvezető lézerdióda, amely modulált lézerfényt bocsát ki, azaz olyan lézernyalábot, melynek amplitúdója nagyfrekvenciával változik. Ha a lézernyalábot egy testre irányítjuk, a keletkező fényfoltról minden irányba szóródik a fény. A (közvetlenül az adó mellett található) vevő beépített optikája a lézerfoltra fókuszál és érzékeli a fényfoltról visszaérkező fényt. A készülékben található elektronika méri a visszaérkező fényjel és a kibocsátott fényjel modulációja közötti

t

időeltolódást, ami éppen azzal az idővel egyezik meg, amely alatt a fény az adóból a vevőbe jut. A mért időeltolódásból ezután a készülék kiszámolja az

\begin{matrix} y = \frac{1}{2} c t + k \end{matrix}

(1)

mennyiséget, amely végül megjelenik a kijelzőn. Ebben a kifejezésben

c = 2, 998 \cdot \cdot 10^{8}

m/s a fénysebesség, az

1 / 2

az oda‐visszaút miatt van, a

k

állandó értéke pedig a készülék beállításától függően kétféle lehet; a készüléken váltani lehet, hogy honnan számítsa a távolságot: az eszköz elülső vagy hátsó oldallapjától. A parallaxis miatt az LTM nem képes 5 cm-nél kisebb távolságok mérésére, a lehető legnagyobb mérhető távolság pedig kb. 25 m. A készülék alakja úgy van kiképezve, hogy az elülső és a hátsó oldallapja is merőleges a lézerfényre, így kényelmesen lehet sík felületű tárgyaktól mérni a távolságot.
A mérés első részében egy kb. 1 méteres optikai kábel belsejében található anyag törésmutatóját kellett meghatározni. Az optikai kábellel összekötve az LTM adóját és vevőjét, a kijelzőn megjelenő távolságérték nem egyezik meg a kábel hosszával. Ennek oka részben az (1) képletben megjelenő, ez esetben feleslegessé váló

1 / 2

-es faktor, részben pedig az, hogy a kábelben terjedő fény sebessége a levegőbeli érték

n

-edrésze, ahol

n

a kábel törésmutatója. A kábelt ollóval lehetett vagdosni, a kábeldarabok hosszát pedig mérőszalaggal lehetett mérni. Az LTM kijelzőjén megjelenő értéket különböző kábelhosszaknál feljegyezve, majd az adatokat ábrázolva, a mérési pontokra illeszkedő egyenes meredekségéből a keresett

c / n

terjedési sebességet és

n

törésmutatót már meg lehetett határozni.
A mérés második részében a víz törésmutatójának meghatározása volt a feladat. A lézeres távolságmérőt ferde helyzetben egy állványra kellett rögzíteni, a lézernyalábot pedig egy téglatest alakú tartályban lévő víz felszínére ejteni (3. ábra). A lézernyaláb a levegő-víz határfelületén megtörve jutott el a tartály aljára, innen a fény egy része visszaszóródva jutott el az LTM vevőjébe. A víz

x

mélységének függvényében az LTM kijelzőjén megjelenő

y

értéket megmérve, geometriai megfontolások segítségével lehetővé vált a víz törésmutatójának meghatározása.

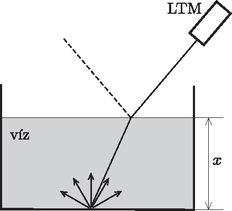3. ábra

Ez a mérési feladat ‐ mind az elméleti hátterét, mind pedig a gyakorlati részét illetően ‐ könnyűnek bizonyult, a magyar csapattagok is jól szerepeltek a feladat megoldásában.

2. feladat. Napelemek vizsgálata

Ebben a feladatban a diákok napelemek különböző tulajdonságait tanulmányozták. Rendelkezésüre állt egy külső fénytől elzárható doboz, ami az ,,optikai pad'' szerepét játszotta. Ebbe a dobozba lehetett elhelyezni a fényforrást, egy vagy két napelemet, és ezek közé még esetleg más optikai eszközöket. A napelemek áramának, feszültségének mérésére két multiméter szolgált.
A versenyzőknek először az egyik napelem

I

áramának a fényforrástól mért

r

távolságtól való függését kellett megmérniük. A mérési adatokra illeszteni kellett egy

I (r) = \frac{I_{a}}{1 + r^{2} / a^{2}}

alakú függvényt, és meg kellett határozni

I_{a}

és

a

paraméterek értékét. Az egyik legcélravezetőbb megoldás

r^{2}

ábrázolása

1 / I

függvényében, ugyanis ezzel lineárissá transzformáljuk a megadott összefüggést.
Ezután a napelem karakterisztikájának vizsgálata volt a feladat. A versenyzők állandó megvilágítás és különböző elektromos terhelés mellett mérték a napelem

I

árama és

U

feszültsége közti összefüggést, és ezt összevetették a megadott elméleti formulával. A felvett karakterisztika segítségével a napelemből kivehető maximális elektromos teljesítményt, valamint az ennek eléréséhez szükséges optimális terhelő ellenállás értékét is meg kellett határozni.
Ezt követően két napelemet egyszerre vizsgáltak a versenyzők. Először össze kellett hasonlítaniuk a napelemek legfontosabb paramétereit (maximális feszültség, maximális áram), majd a két napelemet különbözőképpen (sorosan, párhuzamosan, azonos és ellentétes polaritással) kapcsolva végeztek méréseket a napelemeken.
Az utolsó feladat volt talán a legfurfangosabb. A fényforrás és az egyik napelem közé átlátszó küvettát lehetett tenni, és a küvettában levő vízszint

h

magasságának függvényében kellett mérni a napelem

I

áramát. Ezután a kapott eredmény értelmezését, magyarázatát várták el a versenyzőktől.
Meglepő módon az

I (h)

függvény nem monoton, hanem a 4. ábrán látható módon viselkedik. A kapott görbe az

A

B

C

és

D

pontokkal határolt szakaszok között rendre állandó, csökkenő, gyorsan növő, csökkenő, majd újra állandó, és a teli küvettával mért áram nagyobb, mint az üressel mért.

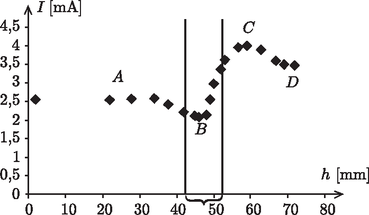4. ábra. A napelem

I

áramának függése a küvettában levő

h

vízszinttől. A kapocs, illetve a két függőleges vonal jelzi a kiterjedt fényforrás függőleges méretét

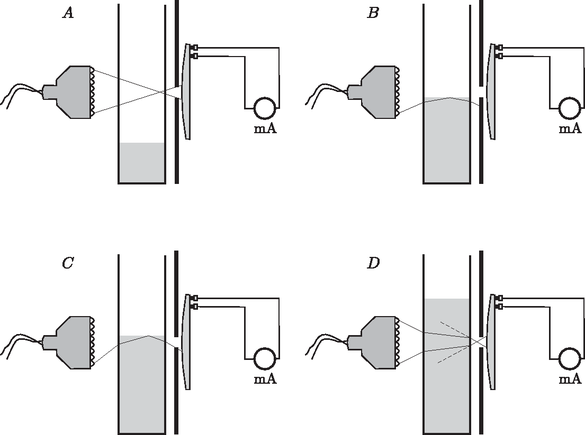5. ábra.

A jelenség magyarázata az 5. ábrasoron látható. Alacsony vízszint esetén (

A

helyzet) a víz magassága nem befolyásolja a napelemre jutó fény mennyiségét. Ha a vízszint kicsit a fényforrás alja fölött van (

B

helyzet), akkor a fény egy része teljes visszaverődést szenved a vízfelszínen, és nem jut el a napelemig. Ha a vízszint kicsivel a fényforrás teteje alatt van, akkor ugyancsak teljes visszaverődés miatt több fény jut a napelembe (

C

helyzet). Végül nagyon magas vízszint esetén a küvetta, mint optikai rendszer, ,,közelebb hozza'' a fényforrást a napelemhez, ez magyarázza, hogy az

I (h)

görbe magasabb értéken telítődik, mint ahonnan indult.
A mérési feladat első része gyors, pontos munkát, grafikus méréskiértékelésben való jártasságot igényelt, az utolsó feladat pedig kifejezetten kreatív gondolkodást.

\begin{matrix} Simon Péter, Tasnádi Tamás, Vigh Máté \end{matrix}

^{$^{*}$}Az elméleti feladatok szövegét a múlt havi számunkban közöltük.