Kezdőlap


Cím:	A 44. Nemzetközi Fizikai Diákolimpiai elméleti feladatai
Füzet:	2013/október, 425 - 436. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 44. Nemzetközi Fizikai Diákolimpia
elméleti feladatai

^{1}

1. feladat. A Maribo-meteorit

Bevezetés. A meteoroid egy kisbolygóból vagy üstökösből kiszakadó kisméretű test (mérete kisebb 1 méternél). A talajba csapódott meteoroidot meteoritnak nevezzük.
2009. január 17-én este a Balti-tenger közelében sok ember látta egy meteoroid izzó csóváját (tűzlabdáját), ahogy áthalad a Föld légkörén. Svédországban egy biztonsági kamera videófelvételt készített az eseményről, amit az 1

(a)

. ábra mutat. A fényképek és szemtanúk beszámolói alapján szűkíteni lehetett a becsapódás helyét, és hat héttel később a dél-dániai Maribo város szomszédságában megtalálták a 0,025 kg tömegű meteoritot, amit azóta Maribonak neveznek. A Maribon végzett mérések, és égi pályájának vizsgálata érdekes eredményt mutat. A meteoroid kivételesen nagy sebességgel hatolt be a légkörbe. A kora

4, 567 \cdot 10^{9}

év, ami azt mutatja, hogy röviddel a Naprendszer születése után keletkezett. A Maribo-meteorit esetleg az Encke-üstökös része volt.
A Maribo sebessége. A tűzgolyó közel nyugati irányban, az északi iránnyal

285^{\circ}

-os szöget bezárva repült a becsapódás helye felé, ahol később megtalálták, ahogy az 1. ábrán látható. A meteoritot a biztonsági kamerától 195 km-re, az északi irányhoz képest

230^{\circ}

-os szögben találták meg.

1. ábra.

(a)

A svédországi biztonsági kamera által készített képek sorozata a Maribo mozgását mutatja, ahogy tűzgömbként áthalad a légkörön.

(b)

A két fényképet jellemző adatok: idő, azimut (fokokban, ahogy a C pontban lévő kamera felöl látni), és a magassági szög (szintén fokokban). Az azimut a horizont síkjában az északi iránytól az órajárással egyezően bezárt szög. A magassági szög a horizont síkjával bezárt szög.

(c)

Vázlat a Maribo mozgásának (az ábrán nyíllal jelölt) irányáról az északi irányhoz (N) viszonyítva és a dániai landolás helye (M), ahogy a kamera (C) látta.
(Lásd még a hátsó belső borító színes fényképeit!)

1.1. A fentiek, valamint az 1. ábra adatainak a felhasználásával határozd meg a Maribo-meteoroid átlagsebességét a

155

. és a

161

. képkocka között eltelt időtartamra! A Föld felszínének görbülete és a meteoroidra ható gravitációs erő elhanyagolható. (1,3 pont)
Megolvad-e az atmoszférában? A meteoroid levegőben való mozgása miatt a felső légkörben fellépő súrlódást bonyolult formula írja le. A közegellenállási erő függ a meteoroid levegőhöz viszonyított sebességétől, valamint a légkör hőmérsékletétől és sűrűségétől. Elfogadható közelítést ad a légkör felső részében a közegellenállási erőre az

F = k ϱ_{atm} A v^{2}

kifejezés, ahol

k

egy állandó (közegellenállási együttható),

ϱ_{atm}

a légkör sűrűsége,

A

a meteoroid sebességre merőleges keresztmetszete, és

v

a sebessége.
A következő egyszerűsítő feltevések felhasználásával vizsgáljuk a meteoroidot: amikor behatol a légkörbe a test, gömb alakú, tömege

m_{M} = 30

kg, sugara

R_{M} = 0, 13

m, hőmérséklete

T_{0} = 200

K, és a sebessége

v_{M} = 2, 91 \cdot 10^{4}

m/s. A légkör sűrűsége állandó (a Föld felszíne felett 40 km magasságban),

ϱ_{atm} = 4, 1 \cdot 10^{- 3} {kg/m}^{3}

, és a közegellenállási együttható

k = 0, 60

.
1.2a. Becsüld meg, hogy a meteoroid légkörbe való behatolását követően mennyi idő múlva változik a sebessége

10 %

-nyit, azaz csökken

v_{M}

-ről

0, 90 v_{M}

-re. A gravitációs erő meteoroidra való hatását elhanyagolhatod, és felteheted, hogy a meteoroid alakja és tömege nem változik. (0,7 pont)
1.2b. Számold ki, hányszor nagyobb a légkörbe hatoló meteoroid

E_{kin}

mozgási energiája a teljes megolvasztásához szükséges

E_{olv.}

energiánál! (Az adatokat a mellékelt táblázatból^{$^{*}$} keresd ki)! (0,3 pont)
A Maribo melegedése a légkörön való áthatolás alatt. Amikor a Maribo-meteoroidkő (röviden: kő) szuperszonikus sebességgel elérte a légkört, akkor egy tűzgömbnek látszott, mert a körülötte levő levegő felizzott. Ennek következtében a Maribo csak a legkülső, felszíni rétegén keresztül vett fel hőt. Tekintsük a Maribot egy homogén gömbnek, amelynek sűrűsége

ϱ_{kő}

, fajhője

c_{kő}

és hővezetési tényezője

k_{kő}

(az adatokat a táblázatból keresd ki)! Továbbá, a légkörbe lépéskor a meteoroid hőmérséklete

T_{0} = 200

K volt. A súrlódás miatt a meteoroid felszíni hőmérséklete a légkörben való esés alatt állandó

T_{s} = 1000

K. Ennek következtében a meteoroid belseje is fokozatosan felmelegszik.
Miután a légkörben már

t

ideig esett, a Maribo felszínén egy

x

vastagságú réteg hőmérséklete válik

T_{0}

-nál jóval melegebbé. Ez a vastagság dimenzióanalízis segítségével megbecsülhető. Feltételezhető, hogy a vastagság nagyságrendje egyszerűen a termodinamikai paraméterek ismeretlen hatványainak szorzata, azaz

x \approx t^{α} ϱ_{kő}^{β} c_{kő}^{γ} k_{kő}^{δ} .

1.3a. Dimenzióanalízis segítségével határozd meg az

α

β

γ

és

δ

kitevők értékét! (0,6 pont)
1.3b. Ez alapján számold ki, hogy mekkora az

x

vastagság

t = 0, 5 s

idővel a légkörbe történő belépés után, valamint határozd meg az

x / R_{M}

arányt! (0,4 pont)
A meteorit kora. A radioaktív izotópok kémiai tulajdonságai különbözhetnek, és így egy adott meteroitban az ásványok kristályosodása során egyes kristályszemcsékben bizonyos radioaktív izotópok koncentrációja magasabb, másokban alacsonyabb. Ez a különbség lehetővé teszi a meteorit korának meghatározását a radioaktív ásványtartalmának elemzésével.
Konkrét példaként vizsgáljuk a

^{87} Rb

izotóp (37-es rendszámú elem) bomlását, amelynek felezési ideje

T_{1 / 2} = 4, 9 \cdot 10^{10}

év, és végterméke a

^{87} Sr

stabil izotóp (38-as rendszámú elem). Ennek mennyiségét viszonyítjuk a meglevő, ugyancsak stabil

^{86} Sr

izotópéhoz. Az ásványok kristályosodásakor a

^{87} Sr /^{86} Sr

arány minden ásványszemcsében azonos volt, míg a

^{87} Rb /^{86} Sr

arány különbözött. Az idő múlásával azonban a

^{87} Rb

izotóp mennyisége csökkent, és ennek következtében a

^{87} Sr

izotóp mennyisége nőtt. Így az ásványszemcsékben mostanra a

^{87} Sr /^{86} Sr

arány különbözővé vált. A 2. ábra vízszintes tengelyein a kristályosodás időpontjában fennállt

^{87} Rb /^{86} Sr

arány van feltüntetve.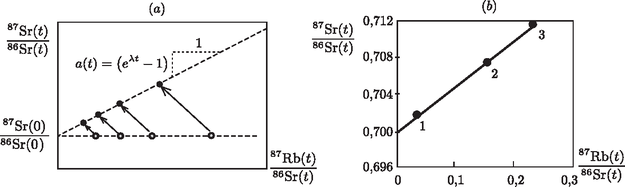

2. ábra.

(a)

A különböző ásványszemcsékben fennálló

^{87} Sr /^{86} Sr

arány a kristályosodás

t = 0

időpontjában (üres körök), illetve jelenleg (tele körök).

(b)

A meteorit három ásványszemcséjében mért, a jelenlegi adatokra illeszkedő egyidejűségi vonal

1.4a. Írd le a

_{37}^{87} Rb

izotóp

_{38}^{87} Sr

-ra való bomlásának egyenletét! (0,3 pont)
1.4b. Mutasd meg, hogy ugyanabból a meteoritból, különböző ásványi szemcsékből származó minták esetén egyenest kapunk, ha a jelenlegi

^{87} Sr /^{86} Sr

arányt a jelenlegi

^{87} Rb /^{86} Sr

arány függvényében ábrázoljuk! Ezt az egyenest egyidejűségi vonalnak nevezzük. Mutasd meg továbbá, hogy az egyidejűségi vonal meredeksége

a (t) = (e^{λ t} - 1)

, ahol

t

a kristályosodás óta eltelt idő,

λ

pedig a bomlási állandó, amely fordítottan arányos a

T_{1 / 2}

felezési idővel! (0,7 pont)
1.4c. Határozd meg a meteorit

τ_{M}

életkorát az 2

(b)

. ábrán látható egyidejűségi vonal alapján! (0,4 pont)
Az Encke-üstökös, ahonnan a Maribo-meteorit származhat. A Nap körül keringő Encke-üstökös Naptól mért legnagyobb és legkisebb távolsága:

\begin{matrix} a_{min} = 4, 95 \cdot 10^{10} m és a_{max} = 6, 16 \cdot 10^{11} m . \end{matrix}

1.5. Számítsd ki az Encke-üstökös

t_{Encke}

keringési idejét! (0,6 pont)
Aszteroida-becsapódás hatása a Földre. 65 millió évvel ezelőtt egy óriási aszteroida csapódott a Földbe. Az aszteorida sűrűsége

ϱ_{aszt.} = 3, 0 \cdot 10^{3} {kg m}^{- 3}

, sugara

R_{aszt.} = 5, 0

km és becsapódási sebessége

v_{aszt.} = 2, 5 \cdot 10^{4}

m/s volt. Ez a becsapódás a földi élet nagy részének kihalását eredményezte, és létrehozta a hatalmas Chicxulub krátert. Képzeljük el, mi történne, ha ma ütközne tökéletesen rugalmatlanul egy ugyanilyen aszteroida a Földnek. Tudjuk, hogy a Föld tehetetlenségi nyomatéka 0,83-szor akkora, mint egy ugyanolyan tömegű és sugarú homogén gömbé. Az

M

tömegű,

R

sugarú homogén gömb tehetetlenségi nyomatéka

(2 / 5) M R^{2}

. Az ütközéskor a Föld pályájának változásától tekintsünk el.
1.6a. Tegyük föl, hogy az aszteroida az északi póluson csapódik be. Határozd meg a Föld forgástengelyének maximális lehetséges szögeltérülését a becsapódás után! (0,7 pont)
1.6b. Tegyük föl, hogy az aszteroida az Egyenlítőre csapódik be radiális (függőleges) irányból. Határozd meg a Föld forgási periódusának

Δ τ_{függ.}

megváltozását az ütközés után! (0,7 pont)
1.6c. Tegyük föl, hogy az aszteroida az Egyenlítőre csapódik be a felszínt érintő (vízszintes) irányból, az Egyenlítő síkjában. Határozd meg Föld forgási periódusának

Δ τ_{érintő}

megváltozását az ütközés után! (0,7 pont)
Maximális becsapódási sebesség. Tekintsünk egy olyan égitestet, amely gravitációsan kötött a Naprendszerhez, és

v_{becs.}

sebességgel becsapódik a Föld felszínére! Kezdetben elhanyagolhatjuk a Földnek a testre gyakorolt gravitációs hatását. Tekintsünk el továbbá a légköri súrlódástól, a többi égitest hatásától és a Föld forgásától!
1.7. Határozd meg a

v_{becs.}

becsapódási sebesség legnagyobb lehetséges

v_{becs.}^{max}

értékét! (1,6 pont)

2. feladat. Plazmonos gőzfejlesztő készülék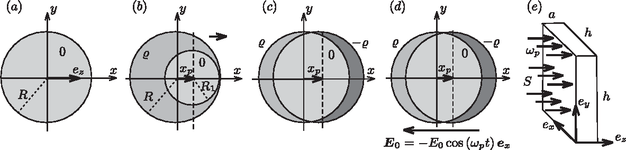

Bevezetés. Ebben a feladatban egy hatékony, kísérletileg is működő gőzfejlesztési eljárást fogunk tanulmányozni. Víz és benne eloszlatott, nanométeres méretű, gömb alakú ezüstgolyócskák (literenként csak körülbelül

10^{13}

darab) keverékét fókuszált fénynyalábbal világítjuk meg. A fény egy részét a nanogolyócskák elnyelik, így felmelegednek és közvetlen környezetükben gőzt keltenek anélkül, hogy a teljes vízmennyiséget felmelegítenék. A keletkező gőz buborékok formájában távozik a rendszerből. Jelenleg a folyamat még nem minden részletében tisztázott, de a felmelegedés jelensége a fémes nanogolyócskák elektronjainak együttes oszcillációján alapuló fényelnyeléssel magyarázható. A berendezést plazmonos gőzfejlesztőnek nevezzük.

3. ábra.

(a)

Egy

R

sugarú, gömb alakú, semleges nanogolyócska a koordináta-rendszer origójában.

(b)

A Tömör gömb homogén, pozitív

ϱ

töltéssűrűséggel (közepesen szürke), benne egy kisebb

R_{1}

sugarú,

x_{d} = x_{d} e_{x}

vektorral eltolt középpontú, gömb alakú, töltéssemleges tartománnyal

(0, halványszürke)

(c)

A koordináta-rendszer origójában rögzített nanogolyócska pozitív

ϱ

töltéssűrűségű ezüstionjai (közepesen szürke), és az origóhoz képest

x_{p}

vektorral eltolt középpontú

(x_{p} ≪ R)

, gömb alakú, negatív

- ϱ

töltéssűrűségű elektronfelhő (sötétszürke).

(d)

Külső homogén

E_{0} = - E_{0} e_{x}

elektromos tér. Időfüggő

E_{0}

esetén az elektronfelhő

v = d x_{P} / d t

sebességgel mozog.

(e)

z

irányba haladó,

ω_{P}

körfrekvenciájú,

S

intenzitású, monokromatikus fénynyalábbal megvilágított téglatest alakú

(h \times h \times a)

tartály, benne a vízben eloszlatott nanogolyócskákkal

Egyetlen, gömb alakú, ezüst nanogolyócska. Ebben a részfeladatban tekintsünk egy

R = 10, 0

nm sugarú, gömb alakú ezüst nanogolyócskát, melynek középpontja a koordináta-rendszerünk origójában van rögzítve, ahogy az a 3

(a)

. ábrán látható. Minden bekövetkező mozgás, erőhatás és erőtér párhuzamos a vízszintes

x

tengellyel (amely az

e_{x}

irányvektorral adható meg). A nanogolyócska vezetési elektronjai a golyócska teljes térfogatában szabadon mozoghatnak anélkül, hogy bármelyik ezüstatomhoz kötődnének. Az ezüstatomok pozitív ionokként vannak jelen a golyócskában, mindegyik egy-egy elektronnal járul hozzá a szabad töltéshordozókhoz.
2.1. Határozd meg a következő mennyiségeket: a nanogolyócska

V

térfogata és

M

tömege; a nanogolyócskában található ezüstionok

N

száma és

ϱ

töltéssűrűsége; valamint a szabad elektronok

n

számsűrűsége (koncentrációja), összes

Q

töltése és összes

m_{0}

tömege. (0,7 pont)
Elektromos mező egy töltött gömbön belüli töltéssemleges tartományban. Ebben a részfeladatban tegyük fel, hogy minden anyag relatív permittivitása

ε = 1

. Homogén

ϱ

töltéssűrűségű,

R

sugarú gömb belsejében

- ϱ

töltéssűrűség hozzáadásával egy kisebb,

R_{1}

sugarú, töltéssemleges tartományt hozunk létre, melynek középpontja az

R

sugarú gömb középpontjához képest

x_{d} = x_{d} e_{x}

vektorral el van tolva (lásd a 3

(b)

. ábrát).
2.2. Mutasd meg, hogy a töltéssemleges tartományban az elektromos tér homogén és

E = A (ϱ / ε_{0}) x_{d}

alakú! Határozd meg az

A

szorzótényező értékét! (1,2 pont)
A kitérített elektronfelhőre ható visszatérítő erő. A következőkben a szabad elektronok együttes mozgását vizsgáljuk. Ennek érdekében modellezzük a szabad elektronok összességét egyetlen, negatívan töltött, homogén

- ϱ

töltéssűrűségű,

x_{p}

középpontú gömbbel, amely az

x

tengely mentén mozoghat az origóhoz rögzített középpontú, pozitív töltésű gömbhöz (ezüstionok) képest (lásd a 3

(c)

. ábrát!). Tegyük fel, hogy egy külső

F_{külső}

erő hatására az elektronfelhő

x_{p} = x_{p} e_{x}

vektorral elmozdul eredeti helyzetéből, ahol

x_{p} ≪ R

. A nanogolyócska ‐ a két szélén megjelenő kicsiny töltéstől eltekintve ‐ a belsejében töltéssemleges marad.
2.3.

x_{p}

és

n

felhasználásával fejezd ki a következő két mennyiséget: az elektronfelhőre ható

F

visszatérítő erőt, valamint az elektronfelhő elmozdítása során végzett

W_{el}

munkát. (1,2 pont)
Ezüst nanogolyócska időben állandó, külső elektromos térben. Egy nanogolyócskát vákuumban

E_{0} = - E_{0} e_{x}

homogén elektromos térbe helyezünk, melynek hatására az elektronfelhő

F_{külső}

erőhatást érezve kicsiny

x_{p}

távolsággal elmozdul, ahol

| x_{p} | ≪ R

.
2.4. Határozd meg az elektronfelhő

x_{p}

elmozdulását

E_{0}

és

n

felhasználásával! Határozd meg az elmozdulás közben a nanogolyócska közepén átmenő

(y, z)

síkon keresztülhaladó

- Δ Q

töltést

R

n

és

x_{p}

függvényében! (0,6 pont)
Az ezüst nanogolyócska helyettesítő kapacitása és induktivitása. Mind időben állandó, mind változó

E_{0}

elektromos térben a nanogolyócska modellezhető egy megfelelő elektromos áramkörrel. A helyettesítő képbeli kapacitás meghatározható, ha a

Δ Q

töltés szétválasztásához szükséges

W_{el}

munkát megfeleltetjük egy

\pm Δ Q

töltéssel ellátott kondenzátor energiájának. A töltésszétválasztás a helyettesítő képben

V_{0}

feszültséget eredményez a fegyverzetek között.
2.5a. Fejezd ki a rendszer helyettesítő képének

C

kapacitását

ε_{0}

és

R

felhasználásával, és számítsd ki numerikus értékét! (0,7 pont)
2.5b.

E_{0}

és

R

felhasználásával fejezd ki azt a

V_{0}

feszültséget, amit a helyettesítő képbeli kondenzátorra kellene kapcsolni ahhoz, hogy

Δ Q

töltése legyen! (0,4 pont)
Időfüggő

E_{0}

elektromos tér esetén az elektronfelhő mozgásba jön, sebességét jelölje

v = v \cdot e_{x}

(lásd a 3

(d)

. ábrát!). Ennek következtében az elektronok

W_{kin}

mozgási energiára tesznek szert és a rögzített

y z

-síkon átfolyó

I

erősségű áramot okoznak. Az elektronfelhő mozgási energiája megfeleltethető egy

I

árammal átjárt

L

induktivitás energiájának.
2.6a. Fejezd ki a

W_{kin}

és

I

mennyiségeket

v

felhasználásával! (0,7 pont)
2.6b. Fejezd ki a helyettesítő képbeli

L

induktivitást a golyócska

R

sugarának, az elektron

e

töltésének és

m_{e}

tömegének, valamint az

n

elektronszám-sűrűség felhasználásával, majd számítsd ki numerikus értékét! (0,5 pont)
Az ezüst nanogolyócska plazmon rezonanciája. Az eddigiekből következik, hogy az egyensúlyi helyzetéből kitérített, majd elengedett elektronfelhő mozgása egy, a rezonanciafrekvenciával oszcilláló ideális LC-körrel modellezhető. Az elektronfelhő ilyen mozgását plazmon-rezonanciának hívják, a rezgés

ω_{p}

körfrekvenciája pedig az úgynevezett plazmon-körfrekvencia.
2.7a. Határozd meg az elektronfelhő

ω_{p}

plazmon-körfrekvenciáját az elektron

e

töltésének,

m_{e}

tömegének, az

n

elektronszám-sűrűség és az

ε_{0}

vákuum-permittivitás felhasználásával! (0,5 pont)
2.7b. Számítsd ki

ω_{p}

-t rad/s egységekben, valamint az

ω = ω_{p}

körfrekvenciájú fény

λ_{p}

hullámhosszát nm egységekben! (0,4 pont)
Plazmon frekvenciájú fénnyel megvilágított ezüst nanogolyócska. A feladat további részében a nanogolyócskát

ω_{p}

plazmon körfrekvenciájú,

S = \frac{1}{2} ε_{0} E_{0}^{2} = 1, 00 {MW m}^{- 2}

intenzitású, monokromatikus fénnyel világítjuk meg. Mivel a hullámhossz nagy (

λ_{p} ≫ R

), tekinthetjük úgy, hogy a nanogolyócska homogén, időben harmonikusan változó

E_{0} = - E_{0} cos (ω_{p} t) e_{x}

elektromos térben helyezkedik el. Az

E_{0}

tér hatására az elektronfelhő

x_{p}

középpontja is ugyanazon frekvenciával,

v = d x_{P} / d t

sebességgel, állandó

x_{0}

amplitúdóval rezegni kezd. Az elektronok eme rezgőmozgása a fény elnyeléséhez vezet. A nanogolyócska által befogott energia egy része a golyócska belsejében Joule-hővé alakul, a maradék része pedig szórt fény formájában újra kisugárzódik.
A Joule-hőt a szabad elektronoknak az ezüstionokkal való ritka, véletlenszerű, rugalmatlan ütközései okozzák. Az ütköző elektron a teljes mozgási energiáját elveszíti, ami az ezüstionok rezgéseivé (azaz hővé) alakul. Az ilyen ütközések közötti átlagos időtartam

τ ≫ 1 / ω_{p}

, ahol ezüst nanogolyóskára számoljunk a

τ = = 5, 24 \cdot 10^{- 15}

s értékkel!
2.8a. Fejezd ki a nanogolyócskában fejlődő Joule-hő keletkezési ütemének (teljesítményének)

P_{hő}

időátlagolt értékét és az áramerősség négyetének

〈 I^{2} 〉

időátlagát úgy, hogy a kifejezések expliciten tartalmazzák az elektronfelhő sebességnégyzetének

〈 v^{2} 〉

időátlagát! (1,0 pont)
2.8b. Határozd meg a nanogolyócska helyettesítő képének ohmikus ellenállását, amely kapcsolatot teremt a fejlődő Joule-hő teljesítménye és az elektronfelhő

I

áramerőssége között. Számítsd ki numerikus értékét! (1,0 pont)
A beeső fénynyalábban a rezgő elektronfelhőn való szóródás (újrakibocsátás) következtében valamekkora

P_{szórt}

időátlagolt teljesítmény formájában veszteség lép fel.

P_{szórt}

nagysága függ a szórócentrum

x_{0}

amplitúdójától,

Q

töltésétől,

ω_{p}

körfrekvenciájától, valamint a fény tulajdonságaitól (a

c

fénysebességtől és a vákuum

ε_{0}

permittivitásától). E négy változóval kifejezve

P_{szórt}

a következő formulával adható meg:

\begin{matrix} P_{szórt} = \frac{Q^{2} x_{0}^{2} ω_{p}^{4}}{12 π ε_{0} c^{3}} . \end{matrix}

2.9.

P_{hő}

analógiájára határozd meg a fényszórásnak megfelelő ekvivalens

P_{szórt}

ohmikus ellenállást

P_{szórt}

felhasználásával! Számítsd ki numerikus értékét is!

\begin{matrix}  \end{matrix}

(1,0 pont)
Az előbbiekben tárgyalt helyettesítő áramköri elemeket sorosan

R L C

-körbe kapcsolva, majd az áramkört (a beeső fény

E_{0}

térerőssége által meghatározott amplitúdójú)

V = V_{0} cos (ω_{p} t)

váltakozó feszültségre kapcsolva megkapjuk az oszcilláló térbe helyezett ezüst nanogolyócska modelljét.
2.10a. Ismert adatok felhasználásával határozd meg a

P_{hő}

és

P_{szórt}

időátlagolt teljesítmény- veszteségek kifejezéseit, valamint az

ω = ω_{p}

körfrekvenciájú beeső fény

E_{0}

amplitúdóját! (1,2 pont)
2.10b. Határozd meg

E_{0}

P_{hő}

, és

P_{szórt}

numerikus értékét! (0,3 pont)
Gőzfejlesztés fénnyel. Az ezüst nanogolyócskákat

n_{ng} = 7, 3 \cdot 10^{15} m^{- 3}

koncentrációban elkeverjük vízben, majd a keveréket egy téglatest alakú,

h \times h \times a = 10 \times 10 \times 10 {cm}^{3}

méretű, átlátszó tartályba töltjük, végül a rendszert merőleges beeséssel plazmon frekvenciájú,

S = 1, 00 {MW m}^{- 2}

intenzitású fénnyel világítjuk meg (lásd a 3

(e)

. ábrát!). A víz hőmérséklete

T_{hő} = 20^{\circ}

C, és a megfigyelésekkel összhangban feltehetjük, hogy stacionárius állapotban a nanogolyócskák Joule-hője teljes egészében

T_{gőz} = 110^{\circ}

C hőmérsékletű gőz keletkezésére fordítódik, a teljes víztömeg hőmérsékletének növelése nélkül.
A plazmonos gőzfejlesztő készülék termodinamikai hatásfokát az

η = = P_{gőz} / P_{összes}

hányadosként definiáljuk, ahol

P_{gőz}

az egész tartályban a gőz fejlesztésére fordítódó hőteljesítmény,

P_{összes}

pedig a tartályra eső fény összes teljesítménye.
Bármely kiszemelt nanogolyócskát az idő legnagyobb részében víz helyett gőz veszi körül, ezért tárgyalható úgy, mintha vákuumban helyezkedne el.
2.11a. Számítsd ki numerikusan a plazmonos gőzfejlesztő készülék által az időegység alatt előállított vízgőz

m_{gőz}

tömegét a plazmon frekvenciájú,

S

intenzitású fénnyel való besugárzás folyamán! (0,6 pont)
2.11b. Számítsd ki numerikusan a plazmonos gőzfejlesztő készülék

η

termodinamikai hatásfokát! (0,2 pont)

3. feladat. A grönlandi jégsapka

Bevezetés. Ez a feladat a grönlandi jégsapkáról, a világ második legnagyobb összefüggő jégtakarójáról szól, ami a 4

(a)

. ábrán látható. Egyszerűsített modellünkben Grönlandot egy

2 L

szélességű és

5 L

hosszúságú téglalapnak tekintjük, ahol a földfelszín a tengerszinttel azonos magasságban van, és a területét teljes mértékben összenyomhatatlan jég borítja (4

(b)

. ábra). A jég

ϱ_{jég}

sűrűségét tekintsük állandónak! A jégsapka

H (x)

magassága nem függ az

y

koordinátától, és a magasság nulláról a maximális

H_{m}

értékig nő, ahogy a parttól,

(x = \pm L)

a téglalap észak-déli felezővonaláig (az

y

tengelyig, a ,,jégválasztóig'') haladunk. Ez a magasságprofil a 4

(c)

. ábrán látható.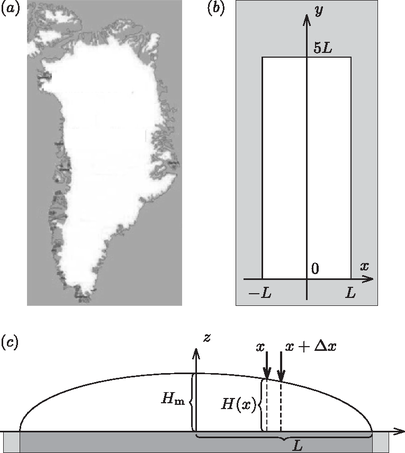

4. ábra.

(a)

Grönland térképe, amely a jégsapka kiterjedését és a jégmentes parti területeket mutatja.

(b)

A grönlandi jégsapka durva modellje; egy jéggel borított,

2 L

és

5 L

oldalú, az

(x, y)

síkban fekvő téglalap. A jégválasztó vonal, azaz a jégsapka maximális,

H_{m}

magasságú gerince az

y

tengely felett fekszik.

(c)

A jégsapka

(x, z)

síkú (függőleges) síkmetszete, melyen a jégtakaró

H (x)

magasságprofilja látható. A

H (x)

magasság független az

y

koordinátától a teljes

0 < y < 5 L

tartományban, és hirtelen nulla értékre esik

y = 0

-ban és

y = 5 L

-ben. Az

y

tengely jelöli a jégválasztó vonal helyét. Az érthetőség kedvéért az ábra függőleges irányú léptéke nagyobb a vízszintes léptéknél. A jég sűrűsége konstans,

ϱ_{jég}

Két hasznos összefüggés. Ebben a részben felhasználhatod a következő integrált:

\begin{matrix} \int_{0}^{1} \sqrt[]{1 - x} d x = \frac{2}{3}, \end{matrix}

és az

{(1 + x)}^{a} \approx 1 + a x

közelítést, amely

| a x | ≪ 1

esetén érvényes.
A jégsapka magasságprofilja. Rövid időskálán a jégsapka egy összenyomhatatlan hidrosztatikai rendszer, melyben a

H (x)

magasságprofil időben állandó.
3.1. Add meg a jégtakaró belsejében a

p (x, z)

nyomást, mint a földfelszíntől (tengerszinttől) mért

z

magasság és a jégválasztó vonaltól mért

x

távolság függvényét! Hanyagold el a légköri nyomást! (0,3 pont)
Most tekints egy rögzített, egyensúlyban levő függőleges jégréteget, amely a kisméretű, vízszintes

Δ x Δ y

alaplap fölött helyezkedik el,

x

és

x + Δ x

között, ahogy ezt a szaggatott vonalak mutatják a 4

(c)

. ábrán! A

Δ y

mérete nem számít. A jégréteg befelé és kifelé eső oldalának magasságkülönbsége miatt e két függőleges oldalon ható eredő erők vízszintes komponensei különböznek. Ezt a

Δ F

különbséget a vízszintes alaplapon ható

Δ F = S_{b} Δ x Δ y

súrlódási erő kompenzálja, amelyet a földfelszín fejt ki a

Δ x Δ y

területű alapra, ahol

S_{b} = 100

kPa.
3.2a. Igazold, hogy rögzített

x

esetén, ha

Δ x \to 0

, akkor

S_{b} = k H d H / d x

, és add meg

k

-t! (0,9 pont)
3.2b. Vezesd le a magasságprofilt megadó

H (x)

kifejezést a

ϱ_{jég}

g

L

S_{b}

, valamint a jégválasztótól mért

x

távolság függvényében! Az eredményből látható, hogy a jégsapka

H_{m}

legnagyobb magassága a

H_{m} \propto L^{1 / 2}

egyenlet szerint skálázódik az

L

félszélességgel. (0,8 pont)
3.2c. Határozd meg azt a

γ

kitevőt, ami szerint a jégsapka teljes

V_{jég}

térfogata skálázódik a téglalap alakú sziget

A

területével,

V_{jég} \propto A^{γ}

! (0,5 pont)
A jégsapka dinamikája. Hosszabb időskálán a jég egy viszkózus, összenyomhatatlan folyadék, amely a gravitáció hatására a középső résztől a tengerparti rész felé áramlik. Ebben a modellben a

H (x)

jégprofil stacionárius alakja dinamikusan valósul meg; a középső területeken hóesés hatására növekvő jégmennyiséget a part mentén bekövetkező hóolvadás kompenzálja. A jégsapka alakjával kapcsolatban továbbra is használjuk a 4

(b)

. és 4

(c)

. ábrán szereplő egyszerűsítéseket, és még alkalmazzuk a következő feltevéseket is modellünkben:
1) A jég az

(x, z)

síkban áramlik, és a jégválasztó vonaltól (az

y

tengelytől) távolodik.
2) Középen a hóesések miatti jégképződés

c

sebessége (méter/év) állandó.
3) A jég csak a partmenti

x = \pm L

területeken, olvadás útján hagyja el a szigetet.
4) A jég áramlási sebességének

v_{x} = d x / d t

vízszintes (

x

irányú) komponense a

z

magasságtól független.
5) A jég áramlási sebességének

v_{z} = d z / d t

függőleges (

z

irányú) komponense

x

-től független.
Vizsgáld csak azt a

| x | ≪ L

középső tartományt a jégsapka tetején, ahol a jégtakaró vastagsága alig változik, közel állandónak tekinthető, azaz

H (x) \approx H_{m}

.
3.3. A tömegmegmaradást használva határozd meg a jég áramlásának

v_{x}

vízszintes sebességkomponensét a

c

x

és

H_{m}

mennyiségek függvényében! (0,6 pont)
A jég összenyomhatatlanságának feltevéséből, (tehát abból, hogy a jég

ϱ_{jég}

sűrűsége állandó), és a tömegmegmaradásból az alábbi összefüggés következik a jég áramlási sebességének komponenseire:

\begin{matrix} \frac{d v_{x}}{d x} + \frac{d v_{z}}{d z} = 0. \end{matrix}

3.4. Add meg, hogyan függ a jégfolyam sebességének

v_{z}

függőleges komponense a

z

magasságtól! (0,6 pont)
Egy kis jégdarab, amely kezdetben a jégfelszín

(x_{i}, H_{m})

pontjában található, az idő múlásával a jégáram részeként egy

z (x)

pályán (trajektórián) mozog a függőleges

(x, z)

síkban.
3.5. Vezesd le ennek a pályának a

z (x)

egyenletét! (0,9 pont)
Kor- és éghajlat-indikátorok a mozgó jégsapkában. A jégfolyam

v_{x} (x)

és

v_{z} (z)

sebességkomponensei alapján megbecsülhető egy adott

H_{m} - z

mélységben található jégdarab

τ (z)

kora.
3.6. Vezesd le a közvetlenül a jégválasztónál

(x = 0)

az alapkőzettől mért

z

magasságban található jégdarab

τ (z)

korát! (1,0 pont)
Grönland jégtáblájának mélyére fúrva az egymásra fagyott múltbéli hórétegeken áthatoló jégmagok (hosszú, henger alakú jégtömbök) emelhetők ki. Az ilyen jégmagok analizálásával feltárhatók a múltbeli éghajlatváltozások, melyek egyik legjobb indikátora a

δ^{18} O

mennyiség, amit a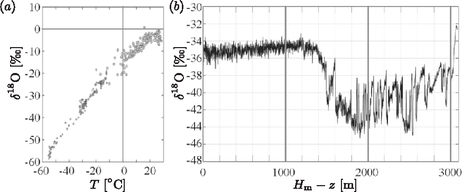

\begin{matrix} δ^{18} O = \frac{R_{jég} - R_{ref}}{R_{ref}} 1000 ‰ \end{matrix}

kifejezés definiál, ahol

R = [^{18} O] / [^{16} O]

jelöli az oxigén két stabil izotópjának, az

^{18} O

-nak és az

^{16} O

-nak a relatív gyakoriságát. Az

R_{ref}

referenciaérték az Egyenlítő környéki óceáni vizekben található izotóp-összetételen alapszik.

5. ábra.

(a)

A hóban mérhető

δ^{18} O

érték és az adott évi átlagos felszíni

T

hőmérséklet megfigyelt kapcsolata.

(b)

δ^{18} O

érték a jég felszínétől mért

H_{m} - z

mélység függvényében egy, a jégválasztónál

(H_{m} = 3060 m)

, a felszíntől az alapkőzetig érő jégmag esetén

A grönlandi megfigyelések szerint a hórétegekben a

δ^{18} O

érték jó közelítéssel lineárisan változik a hőmérséklettel (lásd az 5

(a)

. ábrát). Feltéve, hogy ez az összefüggés mindig igaz volt, egy jégmagból

H_{m} - z

mélységben nyert

δ^{18} O

érték jó becslést szolgáltathat a Grönland környékén ezelőtt

τ (z)

idővel uralkodó

T

hőmérséklet értékére.
Egy 3060 m hosszú grönlandi jégmagon végzett

δ^{18} O

mérések kimutatták, hogy 1492 m mélységben a

δ^{18} O

érték hirtelen ugrik (5

(b)

. ábra), jelezve az utolsó jégkorszak végét. A jégkorszak

120 000

éve kezdődött (ez az időpont 3040 m-es mélységnek felel meg), a jelenlegi jégkorszak-közti időszak pedig

11 700

éve kezdődött (ami 1492 m mélységnek feleltethető meg). Tegyük fel, hogy ez a két időszak különböző jégképződési sebességgel írható le:

c_{jk}

(a jégkorszakban) és

c_{ig}

(a jégkorszak-közti, ún. interglaciális időszakban). Feltehetjük azt is, hogy

H_{m}

értéke állandó volt az utóbbi 120 000 évben.
3.7a. Határozd meg a

c_{jk}

és

c_{ig}

jégképződési sebességeket! (0,8 pont)
3.7b. Az 5. ábra adatait felhasználva határozd meg a jégkorszakból a jégkorszak utáni időszakba történő átmenetkor bekövetkezett hőmérsékletváltozást! (0,2 pont)
Tengerszint-emelkedés a grönlandi jégsapka olvadása miatt. A grönlandi jégtakaró teljes elolvadása az óceánok vízszintjének globális emelkedéséhez vezetne. E szintemelkedés durva becsléseként egyszerűen feltehetjük, hogy a Föld óceánjainak teljes felületén,

A_{óceán} = 3, 61 \cdot 10^{14} m^{2}

-en, mindenhol ugyanannyival emelkedik meg a vízszint.
3.8. Számítsd ki a grönlandi jégtakaró teljes elolvadása esetén bekövetkező átlagos vízszintemelkedést, ha annak jelenlegi területe

A_{G} = 1, 71 \cdot 10^{12} m^{2}

és

S_{b} = 100 kPa

! (0,6 pont)
A nagy tömegű grönlandi jégsapka gravitációsan vonzóerőt fejt ki a környező óceánra. Ha a jégtakaró elolvad, ez a lokális dagály megszűnik és Grönland közelében a tengerszint lesüllyed. Ez az effektus részben ellensúlyozza az előbb kiszámolt szintemelkedést.
A gravitációs vonzás vízszintre gyakorolt hatása nagyságának megbecsléséhez modellezzük a grönlandi jégtakarót egy földfelszínen elhelyezkedő, a teljes grönlandi jégtakaróval megegyező tömegű pontszerű testtel! Koppenhága a Föld felszíne mentén mérve 3500 km-re fekszik ettől a pontszerű testtől. Feltehető, hogy a Föld a pontszerű test nélkül gömbszimmetrikus és egész felszínét,

A_{Föld} = 5, 10 \cdot 10^{14} m^{2}

-t óceán borítja. A Föld forgásából származó minden effektus elhanyagolható.
3.9. A modell keretein belül határozd meg a

h_{CPH} - h_{OPP}

különbséget, azaz a tengerszintek különbségét Koppenhága

(h_{CPH})

és a Grönlanddal a földátmérő mentén átellenben (azaz a Grönlandtól legtávolabb) lévő földrajzi pont

(h_{OPP})

között! (1,8 pont)

Fizikai állandók táblázata

\begin{matrix} Fénysebesség vákuumban & c = 2, 998 \cdot 10^{8} m s^{- 1} \\ Planck-állandó/(2 π) & ℏ = 1, 055 \cdot 10^{- 34} J s \\ Gravitációs állandó & G = 6, 67 \cdot 10^{- 11} m^{3} {kg}^{- 1} s^{- 2} \\ Nehézségi gyorsulás & g = 9, 82 m s^{- 2} \\ Elemi töltés & e = 1, 602 \cdot 10^{- 19} C \\ Vákuum permittivitás & ε_{0} = 8, 854 \cdot 10^{- 12} C^{2} J^{- 1} m^{- 1} \\ Elektron tömege & m_{e} = 9, 109 \cdot 10^{- 31} kg \\ Avogadro-szám & N_{A} = 6, 022 \cdot 10^{23} {mol}^{- 1} \\ Boltzmann-állandó & k_{B} = 1, 381 \cdot 10^{- 23} J K^{- 1} \\ Meteoritkő fajhője & c_{kő} = 1, 2 \cdot 10^{3} J {kg}^{- 1} K^{- 1} \\ Meteoritkő hővezetési tényezője & k_{kő} = 2, 0 W m^{- 1} K^{- 1} \\ Meteoritkő sűrűsége & ϱ_{kő} = 3, 3 \cdot 10^{3} kg m^{- 3} \\ Meteoritkő olvadáspontja & T_{kő} = 1, 7 \cdot 10^{3} K \\ Meteoritkő olvadáshője & L_{kő} = 2, 6 \cdot 10^{5} J {kg}^{- 1} \\ Ezüst moláris tömege & M_{Ag} = 1, 079 \cdot 10^{- 1} {kg mol}^{- 1} \\ Ezüst sűrűsége & ϱ_{Ag} = 1, 049 \cdot 10^{4} kg m^{- 3} \\ Ezüst fajhője & c_{Ag} = 2, 40 \cdot 10^{2} J {kg}^{- 1} K^{- 1} \\ Víz moláris tömege & M_{víz} = 1, 801 \cdot 10^{- 2} kg {mol}^{- 1} \\ Víz sűrűsége & ϱ_{víz} = 0, 998 \cdot 10^{3} kg m^{- 3} \\ Víz hőkapacitása & c_{víz} = 4, 181 \cdot 10^{3} J {kg}^{- 1} K^{- 1} \\ Víz forráshője & L_{víz} = 2, 260 \cdot 10^{6} J {kg}^{- 1} \\ Víz forráspontja & T_{100} = 100^{\circ} C = 373, 15 K \\ Jég, gleccser sűrűsége & ϱ_{jég} = 0, 917 \cdot 10^{3} kg m^{- 3} \\ Gőz fajhője & c_{gőz} = 2, 080 \cdot 10^{3} J {kg}^{- 1} K^{- 1} \\ Föld tömege & m_{F} = 5, 97 \cdot 10^{24} kg \\ Föld sugara & R_{F} = 6, 38 \cdot 10^{6} m \\ Nap tömege & m_{N} = 1, 99 \cdot 10^{30} kg \\ Nap sugara & R_{N} = 6, 96 \cdot 10^{8} m \\ Átlagos Nap‐Föld távolság & a_{N-F} = 1, 50 \cdot 10^{11} m \end{matrix}

¹A hivatalos megoldást és a mérési feladatokat a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre. A három elméleti feladatra összesen 30 pontot lehetett kapni. A részfeladatok után közölt pontszámok az egyes kérdések nehézségi fokára utalnak.

^{$^{*}$}A táblázat a feladatsor végén található.