Cím:	Ízelítő a Kunfalvi Rezső Olimpiai Válogatóverseny feladatsorából
Füzet:	2013/szeptember, 365 - 366. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     Ízelítő a Kunfalvi Rezső Olimpiai Válogatóverseny feladatsorából Budapest, 2013. április 22‐24. 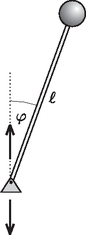    Kapica-inga     Egy súlyos, kicsiny gömbből és egy hozzá képest elhanyagolható tömegű, egyik végén tengelyezett, $\ell$ hosszúságú merev rúdból ingát készítünk. Az inga legalsó helyzetében stabil egyensúlyban van, a legfölső helyzete viszont közismerten instabil: innen elengedve azonnal eldől, akár egy hegyére állított ceruza. Ha azonban az inga felfüggesztési pontját függőlegesen, kis amplitúdóval, nagy frekvenciával rezgetjük, az inga legfelső, $\phi =0^{\circ }$-os helyzete stabillá válik. A jelenség magyarázatát 1951-ben a Nobel-díjas szovjet fizikus, Pjotr Kapica adta meg. Ebben a feladatban a ,,fejenálló'' inga stabilizálásához szükséges feltételeket fogjuk meghatározni kétféle időfüggésű rezgetés esetére.       A rész. Ebben a részben a felfüggesztési pontot függőlegesen úgy rezgetjük, hogy sebessége az idő függvényében periodikusan, háromszögjel szerint változzon. A rezgés periódusidejét $T$-vel jelölve a felfüggesztési pont gyorsulását tehát az $\begin{array}{c}{\displaystyle a\left(t\right)=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle +a_0\mathrm{,}}& {\displaystyle \text{ha }\left(n-\frac{1}{4}\right)T<t<\left(n+\frac{1}{4}\right)T}\hfill \\ \hfill {\displaystyle -a_0\mathrm{,}}& {\displaystyle \text{ha }\left(n+\frac{1}{4}\right)T<t<\left(n+\frac{3}{4}\right)T}\hfill \end{array}}}\end{array}$ függvénnyel adhatjuk meg, ahol $n$ egész szám, a pozitív irányt pedig függőlegesen felfelé választottuk. A gravitáció hatását a A.1., A.2. és A.3. részfeladatokban teljesen hanyagoljuk el!   A.1. Az ingát a legfelső helyzetéből kicsiny ${\phi }_0\ll 1$ szöggel kitérítjük, majd a $t=0$ időpillanatban kezdősebesség nélkül elengedjük. Ábrázoljuk az inga $\phi$ kitérését az idő függvényében és határozzuk meg a kezdőállapothoz viszonyított maximális $\Delta \phi$ szögeltérülést! Tegyük fel, hogy $\Delta \phi \ll {\phi }_0$! Útmutatás: Üljünk bele a felfüggesztési ponttal együttmozgó koordináta- rendszerbe!   A.2. Az előző részfeladatban szereplő közelítéseket felhasználva határozzuk meg az inga helyzetét jellemző $\phi$ szög egy periódusra vett $\langle \phi \left(t\right)\rangle$ időátlagát, valamint az ettől az értéktől való átlagos eltérést, azaz a $\langle |\phi \left(t\right)-\langle \phi \left(t\right)\rangle |\rangle$ mennyiséget!   A.3. Az előző részfeladat eredményét felhasználva határozzuk meg az ingára ható forgatónyomaték egy periódusra vett $\langle M\rangle$ időátlagát a felfüggesztési ponthoz rögzített vonatkoztatási rendszerben!   A.4. Most vegyük figyelembe a gravitáció hatását is! Feltételezhetjük, hogy $g\ll a_0$, így az inga gravitáció hatására bekövetkező szögkitérése sokkal kisebb, mint a A.3. részfeladatban meghatározott $\Delta \phi$ érték. Írjunk föl azt az egyenletet, amely leírja az inga egy periódusra vett átlagos $\langle \phi \rangle$ kitérésének időbeli változását! (Az egyenletet nem kell megoldani.)   A.5. Az előző részfeladatban kapott egyenlet felhasználásával határozzuk meg, milyen egyenlőtlenségnek kell fennállnia $g$, $\ell$, $a_0$ és a rezgés $T$ periódusideje között ahhoz, hogy az inga legfelső helyzete stabil legyen!   B rész. Ebben a részben a felfüggesztési pontot függőlegesen harmonikus időfüggéssel rezgetjük úgy, hogy gyorsulását az idő függvényében az $a\left(t\right)=a_0\text{sin}\left(\omega t\right)$ kifejezés adja meg.   B.1. Írjunk föl egy egyenletet, amely leírja az inga $\phi$ kitérésének időbeli változását a felfüggesztési ponthoz rögzített koordináta-rendszerben! Az egyenletet nem kell megoldani.   B.2. Tegyük fel, hogy az inga $\phi \left(t\right)$ szögkitérésének időfüggése két részre bontható: egy gyorsan oszcilláló részre és egy lassan változó, nem oszcilláló részre, azaz $\begin{array}{c}{\displaystyle \phi \left(t\right)=A\left(t\right)\text{sin}\left(\omega t\right)+B\left(t\right)\mathrm{,}}\end{array}$ ahol $A\left(t\right)$ és $B\left(t\right)$ sokkal lassabban változó függvények, mint $\text{sin}\left(\omega t\right)$. Ezt a próbamegoldást a B.1. részfeladatban kapott egyenletbe helyettesítve és a $g\ll a_0\ll \ell {\omega }^2$ közelítéseket alkalmazva fejezzük ki $A\left(t\right)$-t $B\left(t\right)$, $a_0$, $\omega$ és $g$ felhasználásával!   B.3. Az eddigi közelítéseket alkalmazva írjunk föl egy egyenletet $B\left(t\right)$ időbeli változására, majd $g$, $\ell$ és $a_0$ segítségével fejezzük ki, milyen egyenlőtlenségnek kell fennállnia az $\omega$ körfrekvenciára ahhoz, hogy az inga legfelső helyzete stabil legyen!