Cím: A 43. Nemzetközi Fizikai Diákolimpia elméleti feladatai
Füzet: 2012/október, 427 - 431. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
43. Nemzetközi Fizikai Diákolimpia
elméleti feladatai1
 

1. feladat. Ragadd meg a lényeget! (13 pont)2
 
A rész. Hajítás (4,5 pont). Egy v0 kezdősebességgel elhajított golyó homogén gravitációs térben mozog az x-z síkban, ahol az x-tengely vízszintes, a z-tengely pedig függőleges, a g nehézségi gyorsulással ellentétes irányú. A közegellenállást hanyagold el!
i (0,8 pont). A golyót rögzített v0 nagyságú kezdősebességgel az origó-
ból különböző irányokban elindítva azok a célpontok találhatók el, melyek
a z≤z0-kx2 egyenlőtlenséggel adott tartományban helyezkednek el (ezt a tényt bizonyítás nélkül felhasználhatod). Határozd meg a z0 és k konstansok értékét!
ii (1,2 pont). Ebben a részben a kilövési pont szabadon választható a z=0 talajszinten, és a kilövés szöge is alkalmasan választható. Célunk: a lehető legkisebb v0 kezdősebességgel szeretnénk eltalálni egy R sugarú, gömb alakú épület legfelső pontját (lásd az 1. ábrát). (A célpont elérése előtt a golyó nem pattanhat az épületen.) Vázold fel a golyó optimális pályájának alakját!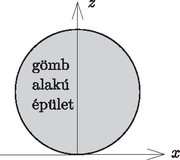


 

1. ábra
 

iii (2,5 pont). Mekkora minimális vmin kilövési sebesség szükséges az R sugarú, gömb alakú épület legfelső pontjának eltalálásához?
B rész. Légáramlás a szárny körül (4 pont). Ebben a részben hasznosak lehetnek a következő információk: Folyadék vagy gáz csőben történő áramlása esetén egy áramvonal mentén p+ρgh+12ρv2=const., feltéve, hogy a v sebesség sokkal kisebb a hangsebességnél. Itt ρ a sűrűség, h a magasság, g a nehézségi gyorsulás és p a nyomás. Az áramvonalakat a részecskék pályájaként definiálhatjuk, amennyiben az áramlás stacionárius. Az 12ρv2 tagot dinamikus nyomásnak nevezzük.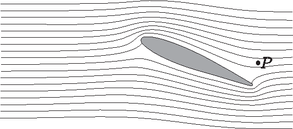


 

2. ábra
 

A 2. ábrán egy repülőgépszárny keresztmetszete látható a szárny körül áramló levegő áramvonalaival együtt, a szárnyhoz rögzített vonatkoztatási rendszerben. Tegyük fel, hogy
a) az áramlás tisztán kétdimenziós (azaz a levegő sebességvektorai a 2. ábra síkjában fekszenek);
b) az áramvonalkép független a repülőgép sebességétől;
c) szél nincs;
d) a dinamikus nyomás jóval kisebb a p0=1,0⋅105 Pa légköri nyomásnál.

(Használj vonalzót az ábrán végezhető mérésekhez!)
i (0,8 pont). Ha a repülőgép sebessége a földhöz viszonyítva v0=100 m/s, mekkora a levegő vP sebessége a 2. ábrán jelzett P pontban a földhöz képest?
ii (1,2 pont). Nagy relatív páratartalom esetén, ha a repülőgép sebessége a földhöz képest túllép egy kritikus vkrit. értéket, a szárny mögött páracseppek sávja keletkezik. A cseppek egy jellemző Q pontban jelennek meg. Jelöld be a 2. ábrán a Q pontot! Magyarázd meg (lehetőleg képletekkel, a lehető legkevesebb szöveggel), hogyan határoztad meg ezt a pontot!
iii (2,0 pont). Becsüld meg a vkrit. kritikus sebesség értékét a következő adatok felhasználásával: a levegő relatív páratartalma r=90%, a levegő állandó nyomáson mért fajhője cp=1,00⋅103 J/(kg K), a telített vízgőz nyomása a meg nem zavart levegő Ta=293 K hőmérsékletén psa=2,31 kPa, Tb=294 K hőmérsékleten pedig psb=2,46 kPa. Az alkalmazott közelítésektől függően szükséged lehet a levegő állandó térfogaton mért cV=0,717⋅103J/(kg K) fajhőjére is. A relatív páratartalom a gőznyomás és a telítési gőznyomás hányadosa egy adott hőmérsékleten. A telítési gőznyomás az a gőznyomás, ahol a gőz egyensúlyban van a folyadékával.
C rész. Mágneses csövek (4,5 pont). Tekintsünk egy szupravezető anyagból készült hengeres csövet! A cső hossza ℓ, belső sugara r; ℓ≫r. Legyen a cső középpontja az origó, tengelye pedig a z tengel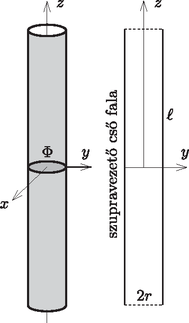y!


 

3. ábra
 

A cső középső keresztmetszetén (z=0, x2+y2<r2) Φ mágneses fluxus halad át. A szupravezető minden mágneses teret kizár magából (a szupravezető anyagban nincs mágneses tér.)
i (0,8 pont). Vázold fel azt az öt mágneses indukcióvonalat, amelyek átmennek a 4. ábrán bejelölt pontokon!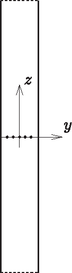


 

4. ábra. A szupravezető hengeres cső hossztengelyére illeszkedő keresztmetszete
 

ii (1,2 pont). Határozd meg a cső közepén ébredő z irányú T erőt, amivel a cső z>0 és z<0 részei hatnak egymásra!
iii (2,5 pont). Most tekintsünk még egy ugyanilyen csövet, amely párhuzamos az elsővel! A második csőben ellentétes irányú a mágneses mező, és a cső középpontja az y=ℓ, x=z=0 pontban helyezkedik el, azaz a csövek egy képzeletbeli négyzet szemközti oldalait alkotják (5. ábra). Határozd meg a csövek között ható F mágneses erőt!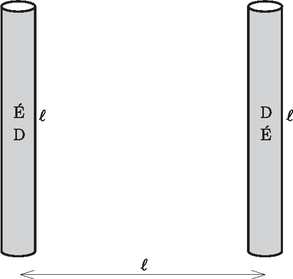


 

5. ábra
 

 
2. feladat. Kelvin csepegtetős gépe (8 pont).
A következő ismeretek hasznosak lehetnek: A folyadék felületét kevésbé kedvelik a részecskék, mint az anyag belsejét. Emiatt a határfelülethez U=σS felületi energia rendelhető, ahol S a határfelület területe és σ a folyadék felületi feszültsége. Továbbá a folyadékfelszín két darabkája F=σl erővel vonzza egymást, ahol l a darabkákat elválasztó egyenes határvonal hossza.

Egy víztartályhoz csatlakozó, d belső átmérőjű, hosszú fémcső függőlegesen lefelé áll; a cső alsó kimeneti nyílásából lassan víz csöpög ki (6. ábra). A vizet elektromosan vezetőnek tekinthetjük; a víz felületi feszültsége σ, sűrűsége ρ. A kimeneti nyílásról lelógó, gömbnek tekinthető vízcsepp sugara r. Mindvégig feltehetjük, hogy d≪r. A vízcsepp nagyon lassan növekszik egészen addig, amíg a g nehézségi gyorsulás hatására le nem esik.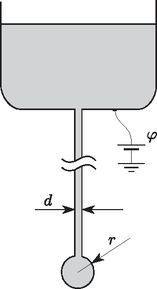


 

6. ábra
 

A rész. Egyetlen cső (4 pont).
i (1,2 pont). Add meg a vízcsepp rmax sugarát abban a pillanatban, amikor leszakad a cső kimeneti nyílásáról.
ii (1,2 pont). A nagyon távoli környezethez képest a cső elektromos potenciálja φ. Határozd meg a csepp Q töltését, amikor a csepp sugara r.
iii (1,6 pont). Ebben az alkérdésben a φ potenciál lassan növekszik, azonban tegyük fel, hogy a csepp r sugara állandó marad. A vízcsepp instabillá válik, és két darabra szakad szét, ha a vízcsepp belsejében a nyomás kisebbé válik, mint a külső légnyomás. Határozd meg azt a φmax potenciált, amikor a szétszakadás bekövetkezik.
B rész. Két cső (4 pont). A két csőből álló berendezést ``Kelvin csepegtetős gépének'' nevezzük, melyben a két cső megegyezik az A részben leírtakkal. A két cső a 7. ábrán látható T-elágazással kapcsolódik a víztartályhoz. Mindkét cső kimeneti nyílása egy-egy fémhenger-elektróda középpontjába esik. A hengerpalástok magassága L, átmérőjük D, L≫D≫r; mindkét cső esetén az időegységenként lecseppenő cseppek száma n. A cseppek H magasságból a kimeneti nyílások alatt elhelyezkedő, elektromosan vezető edényekbe esnek. Az edények az ábrán látható módon az átellenes henger-elektródákkal vannak elektromosan összekötve. A hengerelektródák közé C kapacitású kondenzátor van kapcsolva. A rendszer össztöltése kezdetben nulla. Az első leeső csepp mikroszkopikus töltéssel rendelkezik, amely felborítja a két oldal közötti egyensúlyt és kis töltésszétválást okoz a kondenzátoron. Vedd figyelembe, hogy a tartály földelt!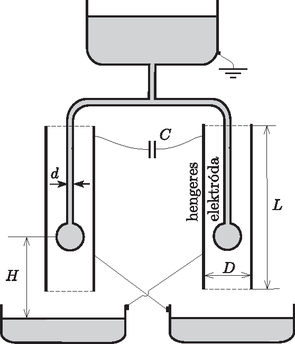


 

7. ábra
 

i (1,2 pont). Fejezd ki a lecseppenő cseppek Q0 töltésének nagyságát akkor, amikor a kondenzátor töltése q. Megoldásodat fejezd ki az A/i. részben meghatározott rmax paraméter segítségével. Tekints el az A/iii. részben leírt effektustól!
ii (1,5 pont). Határozd meg a q töltést a t idő függvényében. Tekintsd a q(t) függvényt folytonosnak, és tételezd fel, hogy q(0)=q0.
iii (1,3 pont). A csepegtető működését az A/iii. részben leírt jelenség akadályozhatja. Az elérhető Umax határfeszültséget a csepp és az alatta lévő edény elektrosztatikus taszító hatása határozza meg. Határozd meg Umax értékét!
 

3. feladat. Csillagkezdemény kialakulása (9 pont).
 

Modellezzük a csillagok keletkezését a következőképpen. Egy gömb alakú csillagközi gázfelhő a saját gravitációja hatására összeroskad. A gázfelhő kezdeti sugara r0, a tömege pedig m. A gázfelhő környezete a gázfelhőnél sokkal ritkább. A környezet és a gázfelhő kezdeti hőmérséklete mindenhol T0. A gázt ideális gáznak tekinthetjük. A gáz átlagos moláris tömege μ, a fajhőhányados γ>43. Tételezzük fel, hogy
Gmμr0≫RT0,
ahol R a gázállandó, G pedig a gravitációs állandó.
 

i (0,8 pont). Az összeroskadás jelentős részében a gáz annyira átlátszó, hogy a keletkező hő azonnal szétsugárzódik, azaz a gázfelhő termodinamikai egyensúlyban marad a környezetével. Miközben a sugár megfeleződik (r1=0,5r0), a nyomás n-szeresére változik. Határozd meg n értékét! Tételezd fel, hogy a gáz sűrűségeloszlása végig homogén marad!
 

ii (2 pont). Becsüld meg azt a t2 időt, amely alatt a sugár az eredeti r0 értékről r2=0,95r0 értékre csökken! Itt hanyagold el a gravitációs tér változását!
 

iii (2,5 pont). Tételezd fel, hogy a nyomás mindvégig elhanyagolható marad! Határozd meg az összeroskadás idejét, azt az időt, amíg a sugár a kezdeti r0 értékről egy sokkal kisebb értekre csökken! Használd a Kepler-törvényeket!
 

iv (1,7 pont). Egy bizonyos r3≪r0 sugárnál a gáz annyira sűrűvé válik, hogy elnyeli a hőmérsékleti sugárzást. Számold ki a kisugárzott hőenergiát az összeroskadás kezdeti szakaszában, amikor a sugár r0 értékről r3 értékre csökken!
 

v (1 pont). Amikor a sugár kisebb, mint r3, a hőmérsékleti sugárzást elhanyagolhatjuk. Határozd meg a gázgömb T hőmérsékletét az r<r3 sugarának függvényében.
 

vi (2 pont). Az összeroskadás végén a nyomás hatását a gáz mozgására nem hanyagolhatjuk el, és az összeroskadás megáll r=r4 sugárnál (r4≪r3). A sugárzást továbbra is hanyagoljuk el, és tegyük fel, hogy a hőmérséklet nem elég magas a magfúzió beindulásához. Egy ilyen csillagkezdeményben a nyomás már nem homogén, de egy szorzó erejéig durva közelítést adhatunk a keresett értékekre.
Adj becslést a végső r4 sugárra és a hozzá tartozó T4 hőmérsékletre!
1A hivatalos megoldást és a mérési feladatokat a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre.

2A feladatokra összesen 30 pontot lehetett kapni. A különböző pontértékek az egyes feladatok és részfeladatok nehézségi fokára utalnak.