Kezdőlap


Cím:	Beszámoló a 2011. évi Eötvös-versenyről
Szerző(k):	Radnai Gyula
Füzet:	2012/március, 169 - 178. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Beszámoló a 2011. évi Eötvös-versenyről

Radnai Gyula

2011. október 14-én délután 3 órai kezdettel került sor a háború utáni 63. Eötvös-versenyre Budapesten és a terv szerint 15, valójában csak 9 vidéki városban. Sajnos Sopronban nem sikerült megrendezni a versenyt, Békéscsabán, Egerben, Nyíregyházán, Székesfehérváron és Szombathelyen pedig egyetlen versenyző sem jelent meg a verseny meghirdetett helyszínén. Feltűnő volt a vidéki diákok érdektelensége; még olyan egyetemi városban is, mint Debrecen, csupán egyetlen versenyző akadt. Az Eötvös-verseny rendezője az Eötvös Loránd Fizikai Társulat, amelynek helyi csoportjai adják a verseny helyi szervezőit. Az ő munkájuk veszett kárba az említett városokban. Szegeden és Pécsett 11-11 versenyző, Budapesten 67 versenyző indult, a többi helyszínen egyaránt 10-nél kevesebben voltak. Először fordult elő, hogy a vidéki helyszíneken együttvéve kevesebb versenyző (41) jelent meg, mint Budapesten.
Az összesen 108 versenyzőből 26-an voltak a két nagy budapesti egyetem (BME, ELTE) elsőéves hallgatói, és pontosan ugyanennyi diák jött a Fővárosi Fazekas Mihály Gyakorló Gimnáziumból. Az egyetemisták közül öten érettségiztek a Fazekasban, négyen az ELTE Apáczai Csere János Gyakorló Gimnáziumban. Innen további hat diák indult a versenyen. A vidéki középiskolák közül a szegedi Radnóti Miklós Kísérleti Gimnáziumból jött a legtöbb (8) versenyző. Külföldi versenyző egyetlen akadt, az ELTE egyik elsőéves hallgatója.
A feladatokat az Eötvös-versenybizottság tűzte ki, és a versenyzők dolgozatait is ugyanez a bizottság értékelte. (Tagjai Honyek Gyula, Károlyházy Frigyes, Vigh Máté, elnöke Radnai Gyula.) A feladatok megoldására 300 perc állt rendelkezésre.
Ismertetjük a feladatokat és azok megoldását.

1. feladat. Pályafutásuk végén a sorsukra hagyott műholdak a sebesség négyzetével arányos légellenállási erő hatására fokozatosan veszítenek mechanikai energiájukból, és végül a légkör sűrűbb rétegeibe érve elégnek. Belátható, hogy az eredetileg körpályákon keringő műholdak a Föld felszínéhez közeledve mindvégig közelítőleg körpályákon haladnak, miközben a ,,körpályák'' sugara lassan csökken.
Tegyük fel, hogy egy

m = 500 kg

tömegű műholdat, amely az Egyenlítő síkjában,

h = 400 km

-es magasságban körpályán kering, magára hagynak! A műholdra ható légellenállási erőt az

F_{lég} = K ϱ v^{2}

alakban adhatjuk meg, ahol

K = 0, 23 m^{2}

ϱ

a levegő sűrűsége a műhold magasságában,

v

pedig a műhold sebessége.

a)

Határozzuk meg a műhold sebességváltozását, miközben pályamagassága a felére csökken

(h \to h / 2)!

b)

A légellenállási erő, valamint a műholdra ható két erő (gravitációs és légellenállási) eredőjének pályamenti (érintőleges) összetevője között egy egyszerű összefüggés állapítható meg. Hogy szól ez?

c)

Mekkora a levegő sűrűsége

h / 2 = 200 km

magasságban, ha itt egy fordulat alatt a műhold pályasugara

100 m

-rel csökken?
A megoldáshoz szükséges további adatokat táblázatokból vehetjük.

(Honyek Gyula)

Megoldás. Adottak:

\begin{matrix} m = 500 kg, h = 400 km = 4 \cdot 10^{5} m, \\ r_{1} = R + h, r_{2} = R + \frac{h}{2}, \\ F_{lég} = K ϱ v^{2} (ahol K = 0, 23 m^{2}), Δ r = - ε (= - 100 m) . \end{matrix}

Táblázatból vehető a Föld egyenlítői

R

sugara,

M

tömege és a gravitációs törvényben szereplő

γ

állandó:

\begin{matrix} R & = 6378 km = 6, 378 \cdot 10^{6} m, \\ M & = 5, 974 \cdot 10^{24} kg, \\ γ & = 6, 673 \cdot 10^{- 11} m^{3} / (kg \cdot s^{2}) . \end{matrix}

a)

A feladatban megfogalmazott feltételek szerint ,,a műholdak a Föld felszínéhez közeledve mindvégig közelítően körpályán haladnak'', ezért jó közelítésben írhatjuk:

\begin{matrix} F_{grav} = m a_{cp}, γ \frac{m M}{r^{2}} = m \frac{v^{2}}{r} . \end{matrix}

Ennek alapján

\begin{matrix} v = \sqrt[]{\frac{γ M}{r}}, \end{matrix}

amelybe behelyettesítve

r_{1}

és

r_{2}

értékeit, megkapjuk a két sebességet:

\begin{matrix} v_{1} = 7669, 0 \frac{m}{s}, v_{2} = 7784, 7 \frac{m}{s} . \end{matrix}

A műhold sebességváltozása tehát

\begin{matrix} v_{2} - v_{1} = 115, 7 \frac{m}{s} > 0. \end{matrix}

A légellenállás következtében nőtt a műhold sebessége! Szokás ezt űrhajózási paradoxonnak is nevezni. A légellenállási, súrlódási erő munkája szükségképpen negatív, mégis nő a műhold mozgási energiája! Hogyan lehetséges ez? Erre kaphatunk választ a feladat

b)

és

c)

részének megoldása során. Érdemes lesz mindkét esetben abból indulunk ki, hogyan változik meg a műhold mechanikai összenergiája, vagyis a kinetikus és potenciális energia összege. Ez az, ami a légellenállási erő hatására csökkenhet.

b)

A légellenállási erő teljesítménye:

\begin{matrix} {\vec{F}}_{lég} \cdot \vec{v} = - F_{lég} \cdot v < 0. \end{matrix}

Ez egyenlő az összenergia változási sebességével:

\begin{matrix} - F_{lég} \cdot v = \frac{Δ E_{össz}}{Δ t} . \end{matrix}

(1)

Az összenergia kinetikus és potenciális részből áll:

\begin{matrix} E_{össz} = E_{kin} + E_{pot} = \frac{1}{2} m v^{2} + (- γ \frac{m M}{r}) . \end{matrix}

E két rész azonban kifejezhető egymásból. Írjuk fel újra a dinamika alaptörvényét:

\begin{matrix} γ \frac{m M}{r^{2}} = m \frac{v^{2}}{r}, azaz γ \frac{m M}{r} = m v^{2}, \end{matrix}

amiből kapjuk:

\begin{matrix} E_{kin} = \frac{1}{2} m v^{2} = \frac{1}{2} γ \frac{m M}{r} = \frac{1}{2} (- E_{pot}) . \end{matrix}

Az összenergiát tehát így is felírhatjuk:

\begin{matrix} E_{össz} = E_{kin} + E_{pot} = E_{kin} - 2 E_{kin} = - E_{kin} < 0. \end{matrix}

(Az, hogy az összenergia negatív, nem kell, hogy megijesszen senkit, az atomfizikában számos példát látunk erre.)
Most tehát (1) így írható:

\begin{matrix} - F_{lég} \cdot v = - \frac{Δ E_{kin}}{Δ t}, \end{matrix}

illetve

\begin{matrix} F_{lég} \cdot v = \frac{Δ (\frac{1}{2} m v^{2})}{Δ t} = m v \frac{Δ v}{Δ t} = m v a_{t} . \end{matrix}

A légellenállásra egy érdekes kifejezést kaptunk:

\begin{matrix} F_{lég} = m a_{t} . \end{matrix}

(2)

m a_{t}

kifejezés a tangenciális (pályamenti) eredő erőt adja, amely most a gravitációs erő pályamenti összetevőjének és a légellenállási erőnek az eredője (1. ábra), tehát

\begin{matrix} m a_{t} = F_{grav ‖} - F_{lég} . \end{matrix}

Ezt vessük össze (2)-vel: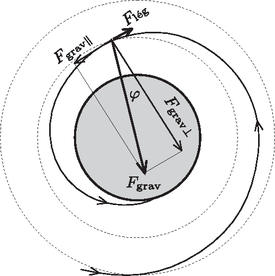

\begin{matrix} F_{lég} = F_{grav ‖} - F_{lég} . \end{matrix}

1. ábra. A feladat számadataival:

F_{grav} = 4, 6

kN,

F_{lég} = 5, 6 mN

φ = 1, 2 \cdot 10^{- 6} rad=0,25''

. A vázlatos ábra nem méretarányos

Az az egyszerű összefüggés tehát, amely a légellenállási erő, valamint a műholdra ható két erő (gravitációs és légellenállási) eredőjének pályamenti összetevője között fennáll az, hogy e kettő nagysága egyenlő egymással.

c)

Ismét az összenergia változásából érdemes kiindulnunk, de az összenergiát most ne a kinetikus, hanem a potenciális energiával fejezzük ki, felhasználva az

E_{kin} = - E_{pot} / 2

összefüggést:

\begin{matrix} E_{össz} = E_{kin} + E_{pot} & = - \frac{E_{pot}}{2} + E_{pot} = \frac{E_{pot}}{2} . \\ \frac{Δ E_{össz}}{Δ t} & = \frac{1}{2} \frac{Δ E_{pot}}{Δ t}, \end{matrix}

ami

Δ r

-rel szorozva és osztva így is írható:

\begin{matrix} \frac{Δ E_{össz}}{Δ t} = \frac{1}{2} \frac{Δ E_{pot}}{Δ r} \frac{Δ r}{Δ t} . \end{matrix}

Mit mondhatunk a sugár változási sebességéről? Ismert adat, hogy egyetlen fordulat során a pályasugár

ε = 100

méterrel csökken, tehát

\begin{matrix} \frac{Δ r}{Δ t} = \frac{- ε}{T} = \frac{- ε}{\frac{2 r π}{v}} . \end{matrix}

Határozzuk meg a potenciális energia és a pályasugár változásának viszonyát:

\begin{matrix} \frac{Δ E_{pot}}{Δ r} = \frac{Δ (- γ \frac{m M}{r})}{Δ r} = γ \frac{m M}{r^{2}} . \end{matrix}

Most már felírhatjuk az (1) egyenletet, amelyben az összenergiát a potenciális energiával fejezzük ki:

\begin{matrix} - F_{lég} \cdot v & = \frac{Δ E_{össz}}{Δ t} = \frac{1}{2} \frac{Δ E_{pot}}{Δ t} = \frac{1}{2} \frac{Δ E_{pot}}{Δ r} \frac{Δ r}{Δ t}, \\ - F_{lég} \cdot v & = \frac{1}{2} γ \frac{m M}{r^{2}} \frac{- ε}{\frac{2 r π}{v}}, \\ F_{lég} & = \frac{1}{4 π} γ \frac{m M}{r^{3}} ε, \\ K ϱ v^{2} & = \frac{1}{4 π} γ \frac{m M}{r^{3}} ε . \end{matrix}

Ebben az egyenletben már csak

ϱ

az egyetlen ismeretlen, éppen ezt kellett kiszámítanunk! De hogy még szebb, elegánsabb formulát kapjunk, használjuk fel újra a

v^{2} = γ M / r

összefüggést, így a következőt kapjuk:

\begin{matrix} ϱ = \frac{1}{4 π K} \frac{m}{r^{2}} ε . \end{matrix}

r = r_{2}

, valamint

ε

megadott értékét behelyettesítve

\begin{matrix} ϱ = 4 \cdot 10^{- 10} \frac{kg}{m^{3}} . \end{matrix}

Kiegészítés: Az

a)

kérdésre

m g = m v^{2} / r

felhasználásával is válaszolhatunk, ha figyelembe vesszük a gravitációs gyorsulás magasságfüggését:

g = g_{0} {(1 - \frac{h}{r})}^{2}

. Ezzel

\begin{matrix} v = \sqrt[]{g r} = (1 - \frac{h}{r}) \sqrt[]{g_{0} r}, \end{matrix}

ahol

g_{0}

az egyenlítői gravitációs gyorsulás, amely azonban a táblázatban adott egyenlítői nehézségi gyorsulásnál nagyobb! A különbség a Föld forgásából adódó ,,centri'' gyorsulás.

2. feladat. Egy függőlegesen álló, henger alakú zárt tartály magassága legyen mondjuk 20 cm! Tegyük fel, hogy a tartály falának és belső tartalmának hőmérséklete huzamos ideje

T = 1^{\circ} C!

A tartalom pedig egy, a tartály alaplapját borító papírvékonyságú vízréteg és fölötte ennek a telített gőze, más semmi. Az oldalfalat hőszigetelőnek tekinthetjük, az alap- és fedőlap azonban igen jó hővezető vékony fémlemez, amelyeknek a hőmérsékletét kívülről szabályozhatjuk.
A lehetőséggel élve emeljük a fedőlap hőmérsékletét

T_{f} = 100^{\circ} C

-ra, miközben az alaplap hőmérsékletét

T = 1^{\circ} C

-on tartjuk, és gondoskodjunk róla, hogy ezek az értékek elég sokáig így maradjanak! Várjuk meg, amíg az edényben kialakul a víz, illetve a gőz új stacionárius állapota, amely már nem változik tovább!

a)

A korábbi egyensúlyi állapothoz képest megváltozott-e említésre méltó mértékben a gőzállapotban lévő vízmolekulák száma, és ha igen, akkor nőtt vagy csökkent?

b)

Vajon mi lenne a válasz, ha a kezdeti állapotban a vízréteg magassága 10 cm lenne?

(Károlyházy Frigyes)

Megoldás. Ha egy folyadék saját telített gőzével érintkezik, akkor a gőz nyomása csak közös hőmérsékletüktől függ. Az alul levő

1^{\circ}

C-os víz felett a gőz nyomása tehát mindkét esetben ugyanannyi. (A táblázatból interpolációval leolvasható ennek aktuális értéke: 660 Pa.)
A gőznyomás az egész edényben ugyanakkora, de abban az esetben, ha a hőmérséklet felfelé emelkedik, a gőz sűrűsége felfelé csökken. (Szintén a táblázatból olvasható ki, hogy az

1^{\circ}

C-os telített gőz sűrűsége 5,2 g/m

^{3}

, amiből egy átlagosan

50, 5^{\circ}

C-os gőz sűrűségére ,,ideális gáz közelítésben'' 4,4 g/m

^{3}

adódik.)
A gőz új stacionárius (időben állandó) állapotában tehát a gőz átlagos sűrűsége kisebb lett, vagyis a gőzállapotban levő vízmolekulák száma csökkent (2. ábra)!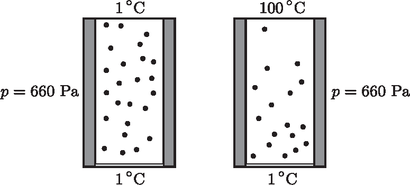

2. ábra

b)

Ha a vízréteg magassága kezdetben 10 cm, a víz kitölti az edény felét. Felette azonban ugyanúgy

1^{\circ}

C hőmérsékletű és 660 Pa nyomású telített gőz van, mint az

a)

esetben.
Amikor viszont a fedőlap hőmérsékletét

100^{\circ}

C-ra emeljük, már nem mondhatjuk, hogy az egész víz

1^{\circ}

C-os marad, ugyanúgy, mint amikor ,,papírvékonyságú'' volt. Azt se állíthatjuk persze, hogy jelentősen felmelegszik a víz felső rétege, mivel a víz sokkal jobb hővezető, mint a vízgőz. Mennyire melegszik hát fel?
Táblázatból kiolvasható, hogy a vízgőz hővezetési együtthatója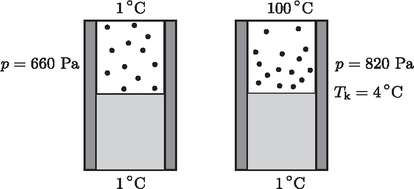

\begin{matrix} λ_{gőz} = 18, 0 \cdot 10^{- 3} \frac{J}{m K s}, \end{matrix}

míg a víz hővezetési együtthatója

\begin{matrix} λ_{víz} = 0, 587 \frac{J}{m K s} = 587 \cdot 10^{- 3} \frac{J}{m K s} . \end{matrix}

Mivel a vízréteg és felette a vízgőz ugyanolyan (10 cm) magas, és a kialakuló hőmérsékletkülönbségek fordítva arányosak a hővezetési együtthatókkal, ezért a víz tetejének és a vele érintkező vízgőznek a közös hőmérsékletét

T_{k}

-val jelölve felírhatjuk:

\begin{matrix} \frac{T_{k} - 1^{\circ} C}{100^{\circ} C - T_{k}} = \frac{λ_{gőz}}{λ_{víz}} = \frac{18 \cdot 10^{- 3}}{587 \cdot 10^{- 3}} . \end{matrix}

Ennek alapján kapjuk

T_{k}

-ra a

4^{\circ} C

-os értéket, amit már a 3. ábrán is feltüntettünk.

3. ábra

Ezek után a táblázatból extrapolációval kiolvashatjuk a

4^{\circ} C

-hoz tartozó telítési gőznyomás nagyságát: 820 Pa. Ez is szerepel már az ábrán.
Hasonlóképpen kiolvashatjuk a telített vízgőz sűrűségének értékét

4^{\circ} C

-on, ez 6,4 g/m

^{3}

. A nyomás az egész gőztérben 820 Pa lesz, a gőz sűrűsége azonban csak legalul 6,4 g/m

^{3}

, felfelé egyre kevesebb. Megbecsülhetjük az átlagos sűrűséget, újra csak ideális gáznak tekintve a vízgőzt, amely átlagosan

50, 5^{\circ}

C hőmérsékletű:

\begin{matrix} ϱ = \frac{274}{323, 5} \cdot 6, 4 \frac{g}{m^{3}} = 5, 4 \frac{g}{m^{3}} . \end{matrix}

Ez viszont még mindig több, mint az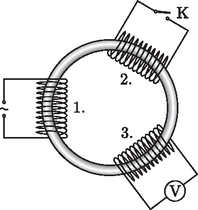

1^{\circ} C

-hoz tartozó 5,2 g/m

^{3}

érték, vagyis ebben az esetben a gőzállapotban levő vízmolekulák száma nőtt!

Kiegészítés: Számításunkban eltekintettünk a víz sűrűségváltozásától, amely persze elhanyagolható a vízgőz sűrűségváltozásához képest. Mégis okozhat egy kis galibát, ha figyelembe vesszük, hogy a

4^{\circ} C

-os legfelső vízréteg sűrűsége nagyobb, mint az alatta levőké. Ezáltal a víz mechanikailag instabillá válik az edényben, s az egyensúlynak kis megzavarása is áramlásokat idézhet elő. Ha valamelyik versenyző erre is utalt volna a dolgozatában, a versenybizottság plusz pontokkal jutalmazta volna, de senkinek se jutott ez akkor eszébe. Hasonlóképpen figyelmen kívül hagyta mindenki a

100^{\circ} C

-os felső lap hősugárzásának hatását a vízréteg hőmérsékletére, azonban ez a hatás nem is olyan jelentős, hogy módosítaná a végső választ: az

a)

esetben csökken, a

b)

esetben nő a vízgőz molekuláinak száma.

3. feladat. Egy toroid (úszógumi) alakú ,,sovány'' vasmagra szimmetrikus elrendezésben három egyforma, ,,kövér'' elektromágneses tekercs van felfűzve a 4. ábra szerint. Az első tekercsre váltóáramú feszültségforrást kapcsolunk, a második tekercs kivezetéseit szabadon hagyjuk, a harmadik tekercs csatlakozóira pedig voltmérőt kötünk. Ekkor a voltmérő a feszültségforrás effektív értékének a felét mutatja.

4. ábra

Ezután a második tekercs kivezetéseit a K kapcsolóval rövidre zárjuk. Mit mutat ebben az esetben a voltmérő?

Útmutatás: A tekercsek ohmos ellenállása elhanyagolható, a feszültségforrást és a voltmérőt ideálisnak tekinthetjük. A vasmag mágneses permeabilitása nem függ a mágneses fluxustól.

(Honyek Gyula)

Megoldás. A könnyebb áttekinthetőség végett a tekercseket már a feladat ábráján megszámoztuk.
A szimmetrikus elrendezés miatt (a középiskolai képlettár jelöléseit követve) a tekercsek önindukciós és kölcsönös indukciós együtthatói között az alábbi összefüggéseket írhatjuk fel:

\begin{matrix} L_{11} & = L_{22} = L_{33}, & jelöljükL-lel; \\ L_{12} & = L_{21} = L_{13} = L_{31} = L_{23} = L_{32}, & jelöljükM-mel . \end{matrix}

Tekintsük az egyes tekercsekben indukált feszültségeket! Minthogy

I_{2} = 0

, mert a kapcsoló nyitva van, valamint

I_{3} \approx 0

, mert a voltmérő ellenállása nagyon nagy, csupán az

I_{1}

áram változása indukál feszültséget.
Az 1. tekercsben

U_{1} = L