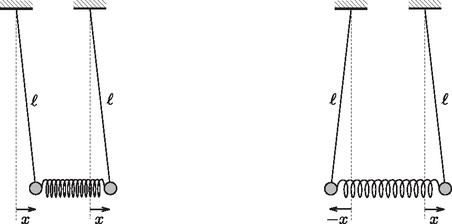A cikk első részében (amely a KöMaL múlt havi számában jelent meg) konkrét példákon keresztül (az egyszerűbbektől a nehezebbek felé haladva) azt vizsgáltuk, hogyan írható le a több testből álló, összetett rezgésekre képes rendszerek mozgása. A cikk végén egészen általános eljárást is adtunk a hasonló problémák megoldásához. Az előző cikk tárgyalásmódját folytatva a már megismert receptet fogjuk alkalmazni a csatolt ingák esetére, majd egy fizikatörténeti példán keresztül mutatunk rá az összetett rezgések fontosságára a szilárdtestfizikában.

 

1. ábra

 

2. ábra

 

Megoldás. Jelöljük az egyes testek kitérését $x_1\left(t\right)$-vel és $x_2\left(t\right)$-vel a 2. ábra szerinti módon! Mivel az ingák mozgásának amplitúdója kicsi, az ingatestek emelkedése-süllyedése sokkal kisebb a vízszintes irányú elmozdulásuknál, ezért alkalmazhatjuk a matematikai inga leírásánál megszokott közelítéseket; az ingatestek függőleges irányú gyorsulását elhanyagoljuk, a fonalakban ébredő erő nagyságát az állandó $mg$ értékkel közelítjük, a fonálerő vízszintes komponensét pedig a kis kitérésekre érvényes $mg\frac{x_i}{\ell }$ összefüggés alapján számítjuk ($i=\mathrm{1,2}$). Így a testek mozgásegyenletei:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle m{\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_1}& {\displaystyle =-\frac{mg}{\ell }{x}_1+D\left(x_2-x_1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle m{\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_2}& {\displaystyle =-\frac{mg}{\ell }{x}_2-D\left(x_2-x_1\right)\mathrm{.}}\hfill \end{array}}$

Osszunk az ingatestek $m$ tömegével!

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle {\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_1}& {\displaystyle =-\frac{g}{\ell }{x}_1+\frac{D}{m}\left(x_2-x_1\right)\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle {\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_2}& {\displaystyle =-\frac{g}{\ell }{x}_2-\frac{D}{m}\left(x_2-x_1\right)\mathrm{.}}\hfill \end{array}}$

A szokásos recept szerint keressük a normálkoordinátákat $y\left(t\right)=x_1\left(t\right)+\alpha x_2\left(t\right)$ alakban (ahol $\alpha$ időtől független állandó)! Ehhez (1) második egyenletét szorozzuk meg $\alpha$-val és adjuk össze az elsővel:

$\begin{array}{c}{\displaystyle {\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_1+\alpha {\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_2=-\frac{g}{\ell }{x}_1+\frac{D}{m}\left(x_2-x_1\right)+\alpha \left(-\frac{g}{\ell }{x}_2-\frac{D}{m}\left(x_2-x_1\right)\right)\mathrm{.}}\end{array}$

Rendezés után alakítsuk át a jobb oldalt úgy, hogy a harmonikus rezgés $\mathrm{<mover\; accent="true">y<mo>¨</mo></mover>}=-{\omega }^{2}y$ egyenletére hasonlító alakot kapjunk!

$\begin{array}{c}{\displaystyle \underset{\mathrm{<mover\; accent="true">y<mo>¨</mo></mover>}}{\overset{}{\underbrace{{\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_1+\alpha {\mathrm{<mover\; accent="true">x<mo>¨</mo></mover>}}_2}}}=-\underset{{\omega }^2}{\overset{}{\underbrace{\left(\frac{D}{m}\left(1-\alpha \right)+\frac{g}{\ell }\right)}}}\underset{y}{\overset{}{\underbrace{\left(x_1+\frac{\frac{D}{m}\left(1-\alpha \right)-\alpha \frac{g}{\ell }}{\frac{D}{m}\left(\alpha -1\right)-\frac{g}{\ell }}{x}_2\right)}}}\mathrm{.}}\end{array}$

Látszik, hogy ha a normálkoordinátákat keressük, az $\alpha$ együttható értékét úgy kell megválasztanunk, hogy teljesüljön az

$\begin{array}{c}{\displaystyle \alpha =\frac{\frac{D}{m}\left(1-\alpha \right)-\alpha \frac{g}{\ell }}{\frac{D}{m}\left(\alpha -1\right)-\frac{g}{\ell }}}\end{array}$

egyenlőség. Ez egy másodfokú egyenlet $\alpha$-ra, melynek két gyöke (függetlenül az $m$, $D$, $\ell$ paraméterektől) ${\alpha }_{\mathrm{1,2}}=\pm 1$. Tehát a normálkoordináták és a nekik megfelelő $\omega$ sajátfrekvenciák a következők:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle y_1\left(t\right)=x_1\left(t\right)+x_2\left(t\right)\mathrm{,}}& {\displaystyle {\omega }_1=\sqrt[]{\frac{g}{\ell }}\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle y_2\left(t\right)=x_1\left(t\right)-x_2\left(t\right)\mathrm{,}}& {\displaystyle {\omega }_2=\sqrt[]{\frac{g}{\ell }+\frac{2D}{m}}\mathrm{.}}\hfill \end{array}}$

A normálkoordináták egy-egy megfelelő ${\omega }_1$, illetve ${\omega }_2$ körfrekvenciájú rezgési egyenletet elégítenek ki, melyek megoldása

$\begin{array}{c}{\displaystyle y_{\mathrm{1,2}}\left(t\right)={\text{A}}_{\mathrm{1,2}}\text{sin}\left({\omega }_{\mathrm{1,2}}t+{\phi }_{\mathrm{1,2}}\right)}\end{array}$

(3)

alakú, itt az ${\text{A}}_{\mathrm{1,2}}$ amplitúdókat és a ${\phi }_{\mathrm{1,2}}$ kezdőfázisokat most is a kezdeti feltételekből határozhatjuk meg. A (2) egyenletekből a normálkoordinátákkal kifejezhetjük az egyes testek kitérését is:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_1\left(t\right)}& {\displaystyle =\frac{1}{2}\left(y_1\left(t\right)+y_2\left(t\right)\right)\mathrm{,}}\hfill & \text{(<mn>4</mn>)}\\ \hfill {\displaystyle x_2\left(t\right)}& {\displaystyle =\frac{1}{2}\left(y_1\left(t\right)-y_2\left(t\right)\right)\mathrm{.}}\hfill \end{array}}$

A konkrét példánk megoldásához már csak a kezdeti feltételekhez kell illesztenünk a normálkoordinátákra vonatkozó általános (3) megoldást. Kezdetben mindkét normálkoordináta zérus, hiszen $x_1\left(0\right)=x_2\left(0\right)=0$, ezért a normálkoordináták kezdőfázisa nulla: ${\phi }_1={\phi }_2=0$. A sebességeket tekintve ${\dot{x}}_1\left(0\right)=v_0$, ${\dot{x}}_2\left(0\right)=0$, így

$\begin{array}{c}{\displaystyle {\dot{y}}_1\left(0\right)={\dot{y}}_2\left(0\right)=v_0={\text{A}}_1{\omega }_1={\text{A}}_2{\omega }_2\mathrm{,}}\end{array}$

azaz az amplitúdók értéke ${\text{A}}_{\mathrm{1,2}}=\frac{v_0}{{\omega }_{\mathrm{1,2}}}$. A normálkoordináták időfüggése tehát:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle y_1\left(t\right)}& {\displaystyle =\frac{v_0}{{\omega }_1}\text{sin}\left({\omega }_{1}t\right)\mathrm{,}}\hfill & \text{(<mn>5</mn>)}\\ \hfill {\displaystyle y_2\left(t\right)}& {\displaystyle =\frac{v_0}{{\omega }_2}\text{sin}\left({\omega }_{2}t\right)\mathrm{,}}\hfill \end{array}}$

így a (4) és (5) egyenleteket felhasználva az ingák kitérése az idő függvényében:

${\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_1\left(t\right)}& {\displaystyle =\frac{v_0}{2{\omega }_1}\text{sin}\left({\omega }_{1}t\right)+\frac{v_0}{2{\omega }_2}\text{sin}\left({\omega }_{2}t\right)\mathrm{,}}\hfill & \text{(<mn>6</mn>)}\\ \hfill {\displaystyle x_2\left(t\right)}& {\displaystyle =\frac{v_0}{2{\omega }_1}\text{sin}\left({\omega }_{1}t\right)-\frac{v_0}{2{\omega }_2}\text{sin}\left({\omega }_{2}t\right)\mathrm{.}}\hfill \end{array}}$

Hátra van még a kérdés: mi a fizikai jelentése az egyes normálkoordinátáknak? A (2) kifejezésére pillantva ezt is könnyen megválaszolhatjuk:

$•$	Ha $y_1\left(t\right)=0$ és $y_2\left(t\right)\ne 0$, akkor a rendszer olyan normálmódusban rezeg, melyben a két ingatest kitérése minden időpillanatban egyenlő nagy és ellentétes irányú.

$•$	Ha $y_2\left(t\right)=0$ és $y_1\left(t\right)\ne 0$, akkor olyan normálmódus jön létre, melyben a két ingatest kitérése minden időpillanatban egyenlő nagy és egyező irányú, ilyenkor tehát a rugó meg sem feszül.

A csatolt inga kétféle normálmódusát a 3. ábra szemlélteti. Tetszőleges kezdeti feltétel esetén tehát a rendszer mozgása e két sajátrezgés megfelelő arányú ,,keverékeként'' (szuperpozíciójaként) írható le.

 

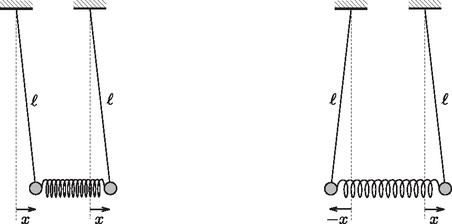3. ábra

 

Lebegés

Ha a két fonálinga közötti csatolás gyenge (azaz ha $D\ll mg/l$), akkor a (2) kifejezésekből adódó körfrekvenciák csak kicsit különböznek egymástól. Vezessük be a két körfrekvencia számtani közepére és különbségére az

${\displaystyle \begin{array}{c}\hfill {\displaystyle \overline{\omega }=\frac{{\omega }_1+{\omega }_2}{2}\mathrm{,}\Delta \omega ={\omega }_2-{\omega }_1\ll \overline{\omega }}\end{array}}$

kifejezéseket! A gyenge csatolás közelítésében alakítsuk át egy kicsit a (6) kifejezéseket! A kis golyók kitérése:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle x_{\mathrm{1,2}}\left(t\right)}& {\displaystyle =\frac{v_0}{2{\omega }_1}\text{sin}\left({\omega }_{1}t\right)\pm \frac{v_0}{2{\omega }_2}\text{sin}\left({\omega }_{2}t\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{v_0}{2\overline{\omega }}\left[\left(1+\frac{\Delta \omega }{2{\omega }_1}\right)\text{sin}\left({\omega }_{1}t\right)\pm \left(1-\frac{\Delta \omega }{2{\omega }_2}\right)\text{sin}\left({\omega }_{2}t\right)\right]\mathrm{,}}\hfill \end{array}}$

ahol a felső előjel az 1-es, az alsó pedig a 2-es golyóra vonatkozik. Elhanyagolva a másodrendűen kicsiny $\Delta \omega /{\omega }_{\mathrm{1,2}}$ alakú tagokat:

$\begin{array}{c}{\displaystyle x_{\mathrm{1,2}}\left(t\right)=\frac{v_0}{2\overline{\omega }}\left[\text{sin}\left({\omega }_{1}t\right)\pm \text{sin}\left({\omega }_{2}t\right)\right]\mathrm{.}}\end{array}$

Használjuk fel a

$\begin{array}{c}{\displaystyle \text{sin}\theta \pm \text{sin}\phi =2\text{sin}\left(\frac{\theta \pm \phi }{2}\right)\text{cos}\left(\frac{\theta \mp \phi }{2}\right)}\end{array}$

trigonometriai azonosságot! Ezzel:

$\begin{array}{c}{\displaystyle x_{\mathrm{1,2}}\left(t\right)=\frac{v_0}{\overline{\omega }}\text{sin}\left(\frac{{\omega }_1\pm {\omega }_2}{2}t\right)\text{cos}\left(\frac{{\omega }_1\mp {\omega }_2}{2}t\right)\mathrm{,}}\end{array}$

tehát a két golyócska kitérés-idő függvénye (ahogy azt a 4. ábra mutatja):

${\displaystyle \begin{array}{cc}\hfill {\displaystyle x_1\left(t\right)}& {\displaystyle =\frac{v_0}{\overline{\omega }}\text{cos}\left(\frac{\Delta \omega }{2}t\right)\text{sin}\left(\overline{\omega }t\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle x_2\left(t\right)}& {\displaystyle =-\frac{v_0}{\overline{\omega }}\text{sin}\left(\frac{\Delta \omega }{2}t\right)\text{cos}\left(\overline{\omega }t\right)\mathrm{,}}\hfill \end{array}}$

 

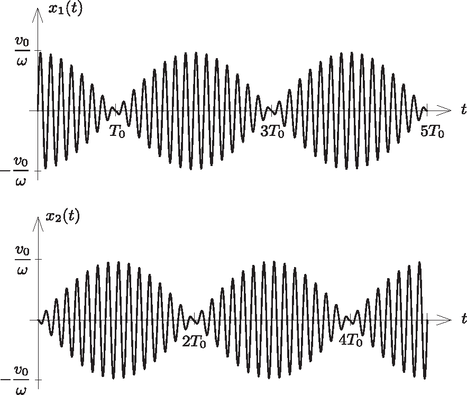4. ábra. A golyócskák kitérése az idő függvényében gyenge csatolás esetén.
Jól látszik az $\overline{\omega }$ körfrekvenciájú gyors rezgésre rárakódó $\Delta \omega$ körfrekvenciájú lebegés.
Az időt a lebegési időtartam ($T_0=2\pi /\Delta \omega$) egységében mértük

Azt kaptuk tehát, hogy a testek mozgása egy $\overline{\omega }$ körfrekvenciájú, gyorsan változó szinuszos (koszinuszos) időfüggvény és egy ehhez képest lassú, $\Delta \omega /2$ körfrekvenciájú koszinuszos (szinuszos) változás szorzata. A lassú változást az amplitúdóba foglalva azt mondhatjuk, hogy a testek $\overline{\omega }$ körfrekvenciával olyan rezgést végeznek, melynek amplitúdója periodikusan ingadozik a zérus és a maximális ($v_0/\overline{\omega }$) amplitúdó között. Amikor az egyik test amplitúdója maximális, a másiké akkor zérus és fordítva: a rezgési energia periodikusan cserélődik a két ingatest között. Ennek a jelenségnek a neve lebegés, a lebegési időtartam (azaz két egymást követő zérus amplitúdójú állapot időkülönbsége) pedig $T_0=2\pi /\Delta \omega$, így $\Delta \omega$-t lebegési (kör)frekvenciának hívják.

 

A kristályok mólhője

Az eddigiekben néhány szabadsági fokú rendszerek összetett rezgéseivel foglalkoztunk. Az eddig megszerzett ismeretek némi matematikai nehézség leküzdése árán kamatoztathatók sok szabadsági fokú, bonyolult rendszereknél is, például egy kristályrácsban elhelyezkedő, rezgő-nyüzsgő atomok sokaságánál. Utóbbi jelentősége különösen nagy a szilárdtestfizikában, amely a XX. századi kialakulása óta mára a fizika egyik legjelentősebb területévé vált és olyan eszközök kifejlesztését tette lehetővé, mint a tranzisztor, mikrochip, merevlemez, LCD-kijelzők, LED-ek, mágneses lebegtetésű vasút stb.

 

Ezt a fejezetet betekintésnek szánjuk a modern szilárdtestfizika egy területére, ezért a fiatalabb Olvasók sok új fizikai és matematikai ismerettel találkozhatnak. A nehezebb részek ne szegjék az Olvasó kedvét, ezek nyugodtan átugorhatók, a figyelmet inkább a végeredményekre és a levont következtetésekre szeretnénk irányítani.

 

A múlt század első éveiben, a kvantummechanika hajnalán egyre növekedett a fizikusokban az igény arra, hogy a makroszkopikus testek viselkedését mélyebben, egészen az őket alkotó részecskék szintjén lehessen értelmezni. 1900-ban Max Planck kvantumhipotézise, amellyel a hőmérsékleti sugárzással kapcsolatos kísérleti eredmények először magyarázhatóvá váltak, olyan lavinát indított el, amely a fizika minden területén forradalmat hozott. Planck elmélete szerint a hőmérsékleti sugárzás adott $f$ frekvenciájú összetevőjét nem folytonosan bocsátják ki vagy nyelik el a testek, hanem apró, $hf$ nagyságú energiaadagokban, ahol $h\approx 6\mathrm{,}626\cdot {10}^{-34}$ Js az általa bevezetett ,,hatáskvantum'' (mai, gyakrabban használt nevén: Planck-állandó).¹
Albert Einstein próbálkozott először a Planck-hipotézis kristályos anyagok hőtani viselkedésének magyarázatára való alkalmazásával. A kristályos anyagokban a rácsatomok szabályos, hosszútávú rendben helyezkednek el. Einstein számolásában azt a feltételezést tette, hogy a kristály atomjai az egyensúlyi helyzetük körül egymástól függetlenül, azonos $f_E$ frekvenciával rezegnek, mintha mindegyik atom egy-egy azonos erősségű rugóval lenne az egyensúlyi helyzethez kötve (lásd az 5. ábra bal oldali részét).²

 

5. ábra. A bal oldalon az Einstein-modell 2 dimenziós (2D) sematikus ábrázolása látható. Az ábra jobb oldalán a kristály csatolt rezgéseit is megengedő (2D) rugó-modell vázlatos rajza szerepel

Klasszikusan egy rugón rezgő test energiája (ami a rugóban tárolt rugalmas energia és a test mozgási energiájának összege) akármekkora lehet, annak nagysága csupán (adott erősségű rugó esetén) a rezgés amplitúdójától függ. Az egyensúlyi helyzetük körül rezgő rácsatomok viszont már nem tekinthetők klasszikus tömegpontnak, rájuk a kvantumfizika törvényei érvényesek. A kvantumhipotézist Einstein a rácsatomok rezgésére a következőképp értelmezte: egyetlen atom (mondjuk $x$-irányú rezgéséhez tartozó) $\epsilon$ rezgési energiája a klasszikus testekkel ellentétben nem lehet akármekkora érték, csak egy bizonyos ${\epsilon }_0=h{f}_E$ ,,energiakvantum'' egész számú többszöröse³:

$\begin{array}{c}{\displaystyle {\epsilon }_n=n{\epsilon }_0\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;"> ahol</span>}n=\mathrm{0,1,2,3,}\text{...}\mathrm{.}}\end{array}$

A rácsatom tetszőleges $n$-hez tartozó energiával rendelkezhet, de ,,szeret'' minél kisebb energiájú állapotban lenni. Bizonyos valószínűséggel azonban a nagyobb energiájú rezgési állapotok is kialakulhatnak. A különböző energiájú állapotok megvalósulási esélyét a gázelméletből ismert Boltzmann-eloszlás szabja meg, mely szerint az $n$-edik, ${\epsilon }_n$ energiájú állapot $p_n$ valószínűsége arányos az $e^{-\frac{{\epsilon }_n}{kT}}$ faktorral⁴, ahol $k$ a Boltzmann-állandó, $T$ pedig a rendszer hőmérséklete.

 

A Boltzmann-eloszlással sokszor találkozhatunk a termodinamika különböző területein. A légkör legegyszerűbb modelljében például, amelyben a levegő hőmérsékletét magasságtól független, állandó értéknek tekintjük, a levegő $\varrho$ sűrűségének $h$ magasságtól való függését a $\varrho \left(h\right)=\varrho \left(0\right)e^{-\frac{mg}{kT}h}$, ún. barometrikus magasságformula írja le (itt $m$ egyetlen gázrészecske tömege, $g$ a nehézségi gyorsulás, $T$ pedig a hőmérséklet). Ha tehát a légkört vízszintesen vékony (mondjuk 10 méter vastag) légrétegekre osztjuk, akkor alulról számítva az $n$-edik rétegben található gázrészecskék száma arányos az $e^{-\frac{mg}{kT}{h}_n}$ szorzótényezővel, ahol $h_n$ az $n$-edik légréteg földfelszíntől mért magassága. Mivel egyetlen gázrészecske gravitációs helyzeti energiája ${\epsilon }_{\text{p}}=mgh$, az arányossági tényező éppen az előbb említett $e^{-\frac{{\epsilon }_{\text{p}}}{kT}}$ Boltzmann-faktor, a részecskék számának (a gáz sűrűségének) magasság szerinti eloszlása pedig Boltzmann-eloszlás. Mivel a levegő hőmérséklete a magassággal erősen változik, a barometrikus magasságformula nem írja le jól a légkör sűrűség- és nyomásviszonyait.

 

Egy rácsatom energiájának várható értékét a lehetséges rezgési energiák Boltzmann-faktorral súlyozott átlagával számolhatjuk:

$\begin{array}{c}{\displaystyle \langle \epsilon \rangle =\sum _{n=0}^{\infty }{p}_n{\epsilon }_n=\frac{\sum _{n=0}^{\infty }{\epsilon }_n{e}^{-\frac{{\epsilon }_n}{kT}}}{\sum _{n=0}^{\infty }{e}^{-\frac{{\epsilon }_n}{kT}}}\mathrm{.}}\end{array}$

A nevezőben szereplő $Z={\sum }_{n=0}^{\infty }{e}^{-\frac{{\epsilon }_n}{kT}}$ összeget szokás állapotösszegnek hívni. Az állapotösszeg esetünkben a mértani sor összegképletével kiszámolható:

$\begin{array}{c}{\displaystyle Z=\sum _{n=0}^{\infty }{e}^{-\frac{n{\epsilon }_0}{kT}}=\frac{1}{1-e^{-\frac{{\epsilon }_0}{kT}}}\mathrm{.}}\end{array}$

(7)

Egy ügyes számolástechnikai trükkel az energia várható értéke könnyen meghatározható. Az összetett függvények deriválására vonatkozó láncszabály segítségével belátható, hogy

$\begin{array}{c}{\displaystyle \langle \epsilon \rangle =-\frac{\text{<span style="font-weight: normal;font-style: normal;">d</span>}}{\text{<span style="font-weight: normal;font-style: normal;">d</span>}(\frac{1}{kT})}\text{ln}Z\mathrm{,}}\end{array}$

(7) felhasználásával:

$\begin{array}{c}{\displaystyle \langle \epsilon \rangle =-\frac{\text{<span style="font-weight: normal;font-style: normal;">d</span>}}{\text{<span style="font-weight: normal;font-style: normal;">d</span>}(\frac{1}{kT})}\text{ln}\left(\frac{1}{1-e^{-\frac{{\epsilon }_0}{kT}}}\right)=\frac{{\epsilon }_0}{e^{\frac{{\epsilon }_0}{kT}}-1}\mathrm{.}}\end{array}$

Mivel az atomok a tér három merőleges irányába függetlenül rezeghetnek, egyetlen atomnak a tér minden irányába megengedett rezgésének várható energiája az előbb kiszámolt érték háromszorosa. Ha veszünk egy mólnyi rácsatomot, akkor azok együttes energiájának várható értéke $T$ hőmérsékleten

$\begin{array}{c}{\displaystyle E=3N_A\langle \epsilon \rangle =3N_A\frac{{\epsilon }_0}{e^{\frac{{\epsilon }_0}{kT}}-1}\mathrm{,}}\end{array}$

ahol $N_A\approx 6\cdot {10}^{23}$ az Avogadro-szám. A mólhő éppen az 1 mólnyi rácsatom energiájának a hőmérséklet szerinti deriváltja:

$\begin{array}{c}{\displaystyle C_M\left(T\right)=\frac{\text{<span style="font-weight: normal;font-style: normal;">d</span>}E}{\text{<span style="font-weight: normal;font-style: normal;">d</span>}T}=3N_{A}k{\left(\frac{{\epsilon }_0}{kT}\right)}^2\frac{e^{\frac{{\epsilon }_0}{kT}}}{(e^{\frac{{\epsilon }_0}{kT}}-1{)}^2}=3R{\left(\frac{{\epsilon }_0}{kT}\right)}^2\frac{e^{\frac{{\epsilon }_0}{kT}}}{(e^{\frac{{\epsilon }_0}{kT}}-1{)}^2}\mathrm{,}}\end{array}$

(8)

itt felhasználtuk, hogy $N_{A}k=R=8\mathrm{,}314\text{J/(mol<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>K)}$ az egyetemes gázállandó. Ez volt Einstein eredménye 1907-ben.

 

Vizsgáljuk meg, mennyi a mólhő értéke magas hőmérsékleten ($kT\gg {\epsilon }_0$)! Ekkor ${\epsilon }_0/kT$ kicsiny, így alkalmazhatjuk az exponenciális függvényre a kis $x$-ekre érvényes $e^x\approx 1+x$ közelítést:

$\begin{array}{c}{\displaystyle C_M\left(T\right)\approx 3R{\left(\frac{{\epsilon }_0}{kT}\right)}^2\frac{1}{(1+\frac{{\epsilon }_0}{kT}-1{)}^2}=3R\mathrm{,}}\end{array}$

ez éppen az 1819 óta ismert, kísérletileg felfedezett Dulong‐Petit szabály!
Alacsony hőmérsékleten ${\epsilon }_0/kT$ nagy értéket vesz fel, ezért ekkor (8) nevezőjében az 1-et elhanyagolhatjuk az exponenciális tag mellett:

$\begin{array}{c}{\displaystyle C_M\left(T\right)\approx 3R{\left(\frac{{\epsilon }_0}{kT}\right)}^2\frac{e^{\frac{{\epsilon }_0}{kT}}}{(e^{\frac{{\epsilon }_0}{kT}}{)}^2}=3R{\left(\frac{{\epsilon }_0}{kT}\right)}^2{e}^{-\frac{{\epsilon }_0}{kT}}\mathrm{,}}\end{array}$

vagyis az abszolút zérus fok felé közeledve a mólhő exponenciálisan tűnik el.

 

Az einsteini számolás minden addiginál mélyebb magyarázatot adott a kristályokon végzett mólhőmérésekre, és a (8) formula az első mérésekkel meglehetősen jó egyezést mutatott (6. ábra). Einstein modelljével az elegáns egyszerűség ellenére nagyon hatékonyan értelmezhetővé vált a mólhő eltűnése kis hőmérsékleten és a Dulong‐Petit szabály teljesülése szobahőmérsékleten. Ez az eredmény a kvantumhipotézis alkalmazásának egyik első sikeres példája volt.

 

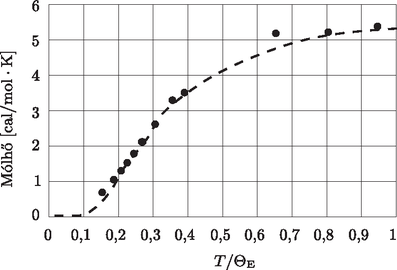6. ábra. A mólhő hőmérsékletfüggése az Einstein-modellben, gyémánt mintán végzett mérési eredményekre illesztve. A hőmérsékletet ${\Theta }_E=h{f}_E/k$ egységekben mértük. (A. Einstein cikke alapján, Annalen der Physik, 22, 1907)

A későbbi, pontosabb mérések eredményei azonban az einsteini elmélettől egyértelmű eltéréseket mutattak (lásd a 7. ábrát). Kitűnt, hogy alacsony hőmérsékleten a modell a mért mólhőnél jóval kisebb értéket jósolt (a kísérleti adatok tanúsága szerint a mólhő az abszolút zérus fok felé közeledve nem exponenciálisan, hanem hatványfüggvény szerint csökkent.)

 

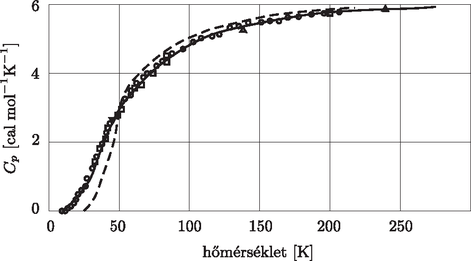
7. ábra. Az ezüst mólhőjének mért értékei a hőmérséklet függvényében. A szaggatott vonal az Einstein-modell alapján számolt, a folytonos vonal pedig a Debye-modellnek megfelelő elméleti görbe

 

Mi lehetett az oka az eltérésnek? Ezzel a kérdéssel vissza is kanyarodtunk cikkünk fő témájához, az összetett rezgésekhez. Talán már az Olvasó is sejti, hogy az a feltételezés, miszerint a rácsatomok egymástól függetlenül, azonos frekvenciával rezegnek, a valóságban nem állja meg a helyét. A kristályrács sokkal jobb modellje az, melyben az atomok úgy rezegnek, mintha egymással rugókkal lennének összekötve. A legegyszerűbb közelítésben csak az elsőszomszédokat kapcsolják össze azonos erősségű rugók (lásd az 5. ábra jobb oldali felén vázolt 2D-s rugós elrendezést). Így a kristályrács összetett, együttes (kollektív) rezgéseket is végez, melyek a (különböző sajátfrekvenciájú) normálrezgésekből keverhetők ki (A három térbeli koordináta miatt az $N$ számú atomot tartalmazó kristály normálmódusainak száma $N$ helyett $3N$). Egyszerűen fogalmazva: alacsony hőmérsékleten, amikor az Einstein-modellben szereplő, egymástól függetlenül rezgő rácsatomok $f_E$ frekvenciájú rezgései már szinte teljesen ,,befagynak'', a valóságban a rácsatomok a kristály alacsonyabb frekvenciájú kollektív rezgéseinek formájában még boldogan ,,nyüzsögnek''.
Ha tehát a kristályos anyagok mólhőjének alacsony hőmérsékleti viselkedését szeretnénk megérteni, figyelembe kell vennünk a rácsatomok összetett rezgéseit is. Ezt a számolást először Peter Debye holland fizikus végezte el 1912-ben, és eredményei az Einstein-modellel szemben nagyon pontosan adták vissza az alacsony hőmérsékleten mért mólhőértékeket (például a $T$ abszolút hőmérséklet növelésével exponenciálisan növekvő mólhő helyett hatványszerű, $T^3$-ös függés adódott az abszolút zérus fok közelében).
Ezzel a fizikatörténeti érdekességgel talán sikerült rávilágítani az összetett rezgések jelentőségére a fizika minden területén. Ezzel a kétrészes cikkünk végére érkeztünk. Befejezésül egy régi KöMaL-feladatot ajánlunk az Olvasó figyelmébe, aminek megoldásával elmélyíthetők az eddig megszerzett ismeretek:

 

P. 3303. Egy $m$ tömegű, $l$ hosszúságú homogén rúd a 8. ábrán látható módon van felfüggesztve egy $l$ hosszú fonálra. A rúd felső végét egy kicsiny $F\Delta t$ erőlökés éri. Írjuk le a rúd legalsó $P$ pontjának mozgását!

 

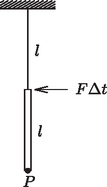8. ábra

 

 

Irodalom

[1]	Budó Ágoston: Kísérleti fizika I., Nemzeti Tankönyvkiadó, Budapest (1997).

[2]	Budó Ágoston: Mechanika, Tankönyvkiadó, Budapest (1988).

[3]	Sólyom Jenő: A modern szilárdtestfizika alapjai I., ELTE Eötvös Kiadó, Budapest (2009).

²A sematikus ábra a magyarázó ereje mellett hiányos is, hiszen az atomok nem csak egy egyenes mentén, hanem a tér három dimenziójának megfelelően három, egymásra merőleges irányban képesek rezegni.

³Valójában a részecskék zérusponti ,,kvantumnyüzsgése'' miatt az ${\epsilon }_n=\left(n+\frac{1}{2}\right)h{f}_E$ kifejezés a helyesebb, ez viszont az elmélet lényegét nem változtatja meg.

⁴Az arányossági tényezőt úgy kell megválasztanunk, hogy a valószínűségek összege 1-et adjon.