Kezdőlap


Cím:	Egy érdekes elektrosztatikai probléma
Szerző(k):	Gnädig Péter
Füzet:	2011/október, 426 - 436. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bevezetés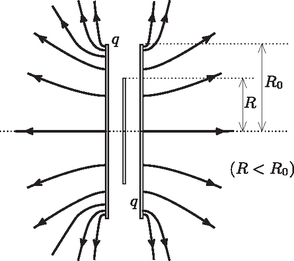

A 2010. évi Eötvös-verseny 3. feladata két párhuzamos, pontosan egymással szemben, egymáshoz közel elhelyezkedő, azonos (mondjuk pozitív)

q

töltéssel ellátott fémkorong közötti erőhatást vizsgálta, ha a korongok közé egy harmadik, semleges fémkorongot helyezünk.¹

1. ábra

Eredetileg a két (azonos töltésű) korong nyilván taszítja egymást. Ez a taszítóerő akkor is megmarad, ha az

R_{0}

sugarú korongok közé egy kisebb,

R < R_{0}

sugarú semleges fémkorongot helyezünk. Ennek igazolásához azt kell belátnunk, hogy az azonos töltésű fémkorongok közötti térrészben gyakorlatilag nulla az elektromos térerősség, tehát az oda helyezett harmadik (semleges) fémtárgy semmilyen változást nem okozhat (1. ábra).
A két korong (a ,,végtelen távoli'' ponthoz viszonyítva) azonos elektromos potenciálú, ez a szimmetrikus helyzetükből következik. Ekkor viszont akár össze is köthetnénk őket egy vékony fémszalaggal a szélüknél vagy annak közelében. (Ha a korongok nagyon közel vannak egymáshoz, akkor az ,,összekötés'' csak a peremük közvetlen közelében, tehát csak nagyon kis térrészben torzítaná el az eredeti elektromos mezőt.) Így egy zárt fémfelületet (Faraday-kalitkát) hozhatnánk létre, amelynek belsejében ‐ mint az jól ismert ‐ nincs elektromos mező.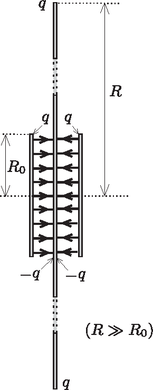

2. ábra

Más lesz a helyzet akkor, ha a semleges korong

R

sugara nagyobb (szélsőséges esetben sokkal nagyobb), mint

R_{0}

. Ilyenkor a középső korong széleiről negatív töltések (nagyságuk majdnem pontosan

- 2 q

) vándorolnak a korong közepére (elektromos megosztás), és így két síkkondenzátor (homogén) elektromos tere alakul ki (2. ábra). A lemezek ilyenkor vonzzák egymást.
Ha az

R

sugár nagyságát ‐ gondolatban ‐ fokozatosan növeljük nagyon kicsiny értékektől indulva egészen a ,,végtelenig'', a szélső fémkorongokra ható, folytonosan változó erő valamikor előjelet vált, tehát egy bizonyos esetben nullává válik. Jelöljük ehhez a kritikus helyzethez tartozó sugarat

R^{⋆}

-gal!
A versenyen nem kérdezték

R^{⋆}

nagyságát, csupán az erőhatás nullává válásának lehetőségét firtatták. Az alábbiakban megmutatjuk, hogy a kritikus sugár lényegében elemi (formális felsőbb matematikai ismereteket nem igénylő, csupán az integrálszámítás alapgondolatát felhasználó) módszerekkel is meghatározható.

Milyen egy töltött fémkorong elektromos tere?

Ha egy nagyon (,,végtelen'') vékony fémkorongot elektromosan feltöltünk, rajta a töltések nem egyenletesen, hanem ‐ mint látni fogjuk ‐ a szélei felé egyre sűrűbben helyezkednek el.

Megjegyzés. Egy naiv érvelés szerint ez azért van így, mert az egymást taszító töltések szeretnének egymástól minél messzebb kerülni, tehát a korong közepéről a korong pereméhez vándorolnak. A helyzet azonban nem ilyen egyszerű, hiszen ugyanilyen érveléssel arra következtethetnénk, hogy a (különböző töltésekkel ellátott) síkkondenzátor lemezein is nagyon egyenetlen a töltéseloszlás; ez pedig nem igaz!

Vajon hogyan, milyen matematikai összefüggéssel írható le a töltések a eloszlása a korongon?
Az egyenetlen töltéseloszlást az egységnyi felületre jutó töltéssel, az ún. töltéssűrűséggel jellemezhetjük, amit

\begin{matrix} η = \frac{Δ Q}{Δ A} \end{matrix}

módon is számolhatunk; itt

Δ A

egy kicsiny felületdarabka nagysága²,

Δ Q

pedig az ezen felületdarabkán található töltés mennyisége. Nem egyenletes töltéseloszlás esetén a töltéssűrűség a felület mentén helyről helyre változik. Egy kör alakú, nagyon vékony fémkorongnál azonban ‐ a forgásszimmetria miatt ‐ a töltéssűrűség csak a korong középpontjától mért

r

távolságtól függhet. A továbbiakban ezt az

η (r)

függvényt fogjuk meghatározni egy

R

sugarú,

Q = 2 q

össztöltésű fémkorongra.
Tekintsünk először egy

R

sugarú,

Q

össztöltésű fémgömböt, amelynek felületén (szimmetria-okokból) egyenletesen oszlanak el a töltések, vagyis a töltéssűrűség

\begin{matrix} η_{0} = \frac{Q}{4 π R^{2}} = \frac{q}{2 π R^{2}} = állandó. \end{matrix}

A gömb belsejében ‐ mint az jól ismert ‐ nulla az eredő elektromos térerősség. Ezt úgy láthatjuk be, hogy kiszámítjuk a gömb egy belső

P

pontjából valamelyik irányban látható (igen kicsiny)

Δ A_{1}

méretű felületdarabkán levő

\begin{matrix} Δ Q_{1} = η_{0} Δ A_{1} \end{matrix}

nagyságú töltés, illetve a vele ellentétes irányban látszó

\begin{matrix} Δ Q_{2} = η_{0} Δ A_{2} \end{matrix}

nagyságú töltés eredő elektromos terét a

P

pontban (3. ábra). Ez az eredő (Coulomb törvénye szerint):

\begin{matrix} k \frac{Δ Q_{1}}{r_{1}^{2}} - k \frac{Δ Q_{2}}{r_{2}^{2}} = k η_{0} (\frac{Δ A_{1}}{r_{1}^{2}} - \frac{Δ A_{2}}{r_{2}^{2}}) = 0. \end{matrix}

Az utolsó lépésben kihasználtuk, hogy (geometriai megfontolásból adódóan)

\begin{matrix} \frac{Δ A_{1}}{Δ A_{2}} = \frac{r_{1}^{2}}{r_{2}^{2}} . \end{matrix}

A fenti egyenlőség belátásához azt kell végiggondolnunk, hogy a

P

pontból adott (kicsiny) térszögben látszó,

A

pont körüli felületdarabka területe
‐ a térszög definíciója szerint ‐ a

P A

négyzetével arányos, ha a felület merőleges
a

\vec{P A}

irányra. Igaz ugyan, hogy a gömbfelület érintősíkja általában nem merőleges

\vec{P A}

-ra, hanem valamekkora szöget zár be vele, de ez szög az átellenes felületdarabkánál is ugyanakkora, tehát az innen származó torzítási szorzófaktor a fenti arányból kiesik.

Az egymással szemközti kicsiny felületdarabkákon levő töltések erőhatásai páronként kiejtik egymást; a gömbfelületen levő összes töltéstől származó eredő elektromos térerősség tehát nulla.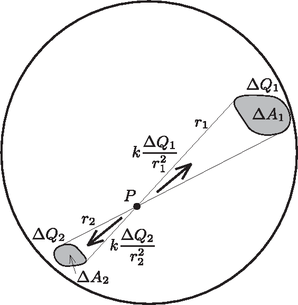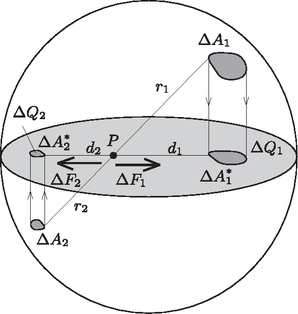

3. ábra

4. ábra

Térjünk most rá az elektromosan töltött korong esetére! Megmutatjuk, hogy ennek töltéseloszlása könnyen megkapható az egyenletesen töltött fémgömb eloszlásából. ,,Ragasszuk'' rá (gondolatban) a töltéseket a gömbfelületre, majd vetítsük le merőlegesen a gömbfelület pontjait egy olyan síkra, amely a gömb középpontjára is és a korábban vizsgált

P

pontra is illeszkedik (4. ábra).
Mivel a töltések nem tudnak elmozdulni, az eredetileg

Δ A_{1}

nagyságú felületen található

Δ Q_{1}

töltés a síkra vetítve változatlan mennyiségben, de valamennyivel kisebb

Δ A_{1}^{*}

területen fog elhelyezkedni, tehát megnő a töltéssűrűsége; emellett a

P

ponttól mért távolsága is megváltozik, az eredeti

r_{1}

helyett egy kisebb érték,

d_{1}

lesz. Ugyanez történik a gömbfelület átellenes pontjaiban található,

Δ Q_{2}

nagyságú töltéssel is.
Vajon mekkora eredő elektromos térerősséget hoz létre ez a két (levetített, de még a koronghoz ragasztott) töltésdarabka a sík

P

pontjában? Ismét a Coulomb-törvényből számolhatjuk az eredőt:

\begin{matrix} k \frac{Δ Q_{1}}{d_{1}^{2}} - k \frac{Δ Q_{2}}{d_{2}^{2}} = k η_{0} (\frac{Δ A_{1}}{d_{1}^{2}} - \frac{Δ A_{2}}{d_{2}^{2}}) = 0. \end{matrix}

Az utolsó lépésnél (geometriai megfontolások alapján) kihasználtuk, hogy

\begin{matrix} \frac{Δ A_{1}}{Δ A_{2}} = \frac{r_{1}^{2}}{r_{2}^{2}}, továbbá \frac{r_{1}}{r_{2}} = \frac{d_{1}}{d_{2}} . \end{matrix}

Ugyanez igaz a többi töltés-pár erőterére, tehát a teljes töltéseloszlás elektromos mezőjére is: a korong síkjában az elektromos térerősség nulla.
Azt az érdekes eredményt kaptuk, hogy a

P

pontban rögzített töltéseket a többi töltés elektromos tere semerre nem akarja elmozdítani. Node akkor a töltések rögzítését (leragasztását) akár meg is szüntethetjük, azok ‐ erőhatás hiányában ‐ úgysem mozdulnak el. Ezzel megoldottuk az elektromosan töltött körlap problémáját: azon a töltések éppen úgy oszlanak el, mintha egy egyenletesen töltött gömbfelületről kerültek volna oda merőleges vetítéssel.
A fémkorong töltéssűrűsége is könnyen leolvasható egy olyan ,,oldalnézeti'' rajzról, amelyen a kérdése felületdarabkák éppen egy-egy vonalnak látszanak (5. ábra). Azok a töltések, amelyek eredetileg

Δ A

nagyságú területen helyezkedtek el, és a vetítés után az

R

sugarú korong középpontjától

r

távolságra kerülnek, az új helyükön

\begin{matrix} Δ A^{*} = sin α \cdot Δ A = \frac{\sqrt[]{R^{2} - r^{2}}}{R} Δ A \end{matrix}

nagyságú területre jutnak. A fémkorong töltéssűrűsége tehát

\begin{matrix} η (r) = \frac{Δ Q}{Δ A^{*}} = η_{0} \frac{Δ A}{Δ A^{*}} = \frac{Q}{4 π R^{2}} \frac{R}{\sqrt[]{R^{2} - r^{2}}}, \end{matrix}

vagyis

\begin{matrix} η (r) = \frac{q}{2 π R} \cdot \frac{1}{\sqrt[]{R^{2} - r^{2}}} \end{matrix}

(1)

lesz (6. ábra).

5. ábra

6. ábra

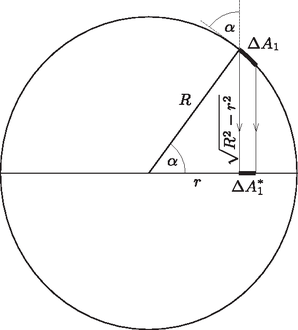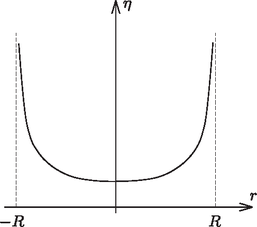A töltéssűrűség az előzetes várakozásunknak megfelelően a korong közepétől a széle felé haladva egyre nő, a peremen ,,végtelen naggyá'' válik. Ezt a végtelent azonban nem szabad komolyan venni, mert amikor

r

már csak annyival kisebb

R

-nél, mint a korong (eddig nullának tekintett, de a valóságban természetesen véges) vastagsága, akkor a fenti számolás érvényét veszti.
Figyelem! Az (1) képletben szereplő töltéssűrűség a fémkorong egyik (mondjuk felső) oldalának a töltéssűrűsége, hiszen a gömb egyik (felső) felén levő, összesen

Q / 2 = q

nagyságú töltés ,,levetítéséből'' származik. A korong másik (alsó) felén ugyancsak

q

töltés fog elhelyezkedni, a felső oldallal azonos eloszlásban.

Megjegyzés. Érdekes kérdés: mi történne az egyenletesen töltött gömb töltéselrendezésével, ha azt a gömb egyik átmérőjére, vagyis egy vonalra vetítenénk. Az erők páronkénti kiejtése látszólag itt is működik, amiből arra következtethetnénk, hogy egy nagyon vékony fémszálon (pl. egy varrótűn) a töltések egyenletes vonalmenti töltéssűrűséggel helyezkednek el (hiszen a gömbövek felszíne a magasságukkal arányos). Ez pedig biztosan nem lehet igaz, hiszen pl. a tű hosszának egyik harmadolópontjában a 2/3 hosszúságú részen levő töltések nagyobb erőt fejtenek ki, mint az

1 / 3

hosszon levők. Vajon hol a hiba?

Elektrosztatikus erőhatások

Mekkora nagyságú és milyen irányú erőt fejt ki egy fémfelületre a körülötte levő elektrosztatikus mező? Tekintsük a fémfelület kicsiny,

Δ A

nagyságú darabkáját, amelyen

Δ Q = η Δ A)

töltés található (

η

a felületi töltéssűrűség). Ha a felület közvetlen közelében

E

nagyságú az elektromos térerősség (és a fém belsejében természetesen nulla), akkor a töltésre ható erő az átlagos térerősségből számolható:

\begin{matrix} Δ F = \frac{1}{2} E \cdot Δ Q = \frac{η}{2} E \cdot Δ A . \end{matrix}

Másrészt ‐ Gauss törvénye szerint ‐ igaz, hogy egy bizonyos mennyiségű töltésből kiinduló elektromos fluxus (másnéven az erővonalak száma) a töltéssel arányos:

\begin{matrix} E \cdot Δ A = 4 π k \cdot Δ Q = 4 π k η Δ A, vagyis E = 4 π k η, \end{matrix}

ahol

k

a Coulomb-törvényben szereplő állandó (

k = 9 \cdot 10^{9}

N m

^{2}

^{- 2}

). A fenti két képletet egybevetve az erőhatás így számolható:

\begin{matrix} Δ F = 2 π k η^{2} \cdot Δ A . \end{matrix}

(2)

Látható, hogy az erő nagysága a felülettel arányos (éppen úgy, mint pl. a folyadékok nyomásából származó, vagy egy megfeszített acélszálban ható rugalmas húzóerő), iránya pedig a felületre merőleges. (Figyelemre méltó, hogy az erő iránya független a töltés (töltéssűrűség) előjelétől, minden esetben a fém belsejéből kifelé mutat.)

Megjegyzés. Az egységnyi felületre ható erőt, vagyis a

2 π k η^{2} = E^{2} / (8 π k)

mennyiséget Maxwell-féle feszültségnek nevezik. J. C. Maxwell a rugalmas testek alakváltozásakor fellépő feszültségek mintájára írta fel az elektromágneses jelenségek néhány fontos törvényét. Az általa megfogalmazott törvények a fizika mindmáig helyesnek talált alapösszefüggései, jóllehet a hozzájuk vezető (az ún. éter rugalmas alakváltozásaira alapozott) gondolatmenet felett eljárt az idő.

Egy kiterjedt fémfelületre, pl. az 1. ábrán látható jobb oldali korongra ható eredő erőt elvben úgy számolhatjuk ki, hogy összegezzük a (2) egyenletben szereplő kicsiny erőket a teljes felületre. Ehhez természetesen ismernünk kell a töltések eloszlását a fémfelületen, vagyis tudnunk kell az

η

töltéssűrűség-függvényt.

Megjegyzés. Az 1. ábrán látható jobb oldali korongra ható erő jobb felé mutat, és a nagyságát a belőle kiinduló erővonalsűrűség határozza meg. Naivan akár azt is gondolhatjuk, hogy a jobb oldali korongot nem a bal oldali korong töltései taszítják, hanem a saját maga által létrehozott elektromos mező húzza jobb felé. Ez azonban erőltetett magyarázat, hiszen a jobb oldali korongból kiinduló erővonalak éppen azért haladnak jobbfelé, mert ott van a másik töltött korong is. Ha annak töltése ellentétes lenne, akkor az erővonalak a két korong közötti térrészben haladnának (síkkondenzátor), s a korongra ható erő vonzó lenne.

Az Eötvös-verseny feladatában szereplő fémkorongokra ható erő

A hosszas előkészítés után most már lényegében minden eszköz rendelkezésünkre áll, hogy kiszámítsuk, mekkora erő hat az egyenként

q

töltésű,

R_{0}

sugarú, koncentrikusan elhelyezkedő, egymáshoz igen közeli párhuzamos fémkorongok között, ha közéjük egy semleges,

R

sugarú

(R > R_{0})

harmadik fémkorongot helyezünk. Csupán egyetlen ‐ fontos ‐ észrevétel hiányzik, annak felismerése, hogy a három korong együttes elektrosztatikus tere a korongokon kívül gyakorlatilag megegyezik egyetlen

R

sugarú,

2 q

össztöltésű fémkorong elektromos terével (7. ábra).³ (A ,,gyakorlatilag'' szó arra utal, hogy a két elrendezés erőtere között csak a korongok széleinél lesz eltérés, de ott is csak egy nagyon kicsi, a korongok távolságával összemérhető tartományban.)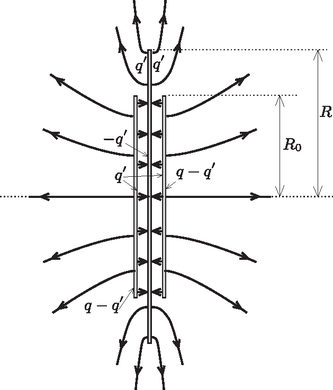

7. ábra

A töltések eloszlását az egyik (mondjuk a jobb oldali) korong külső részén és a középső korong ,,kilógó'' részén tehát éppen az (1) összefüggésnek megfelelő

η (r)

töltéssűrűség-függvény írja le. A töltéssűrűségből kiszámíthatjuk, hogy mekkora

q'

töltés jut a középső korong kilógó

(R_{0} < r < R)

részének egy-egy oldalára, és mennyi

(q - q')

töltés marad a szélső korongok külső felületein. Természetesen a belső oldalakon is meg kell jelenjenek töltések, a középső (összességében semleges) korongon

- q'

, a szélső korongok belső felületein pedig

+ q'

.
Fontos észrevétel, hogy a belső felületeken megjelenő töltések eloszlása egyenletes kell legyen, hiszen a lemezek közötti konstans feszültség helytől független elektromos térerősséget, tehát (a Gauss-törvény értelmében) helytől független töltéssűrűséget követel meg.
Az egyes lemezdarabokra jutó töltés nagyságát ‐ a töltéssűrűség ismeretében ‐ összegzéssel kaphatjuk meg: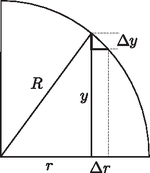

\begin{matrix} Q = \sum Δ Q = \sum_{a felületre}^{} η \cdot Δ A, \end{matrix}

ahol

Δ A

a fémfelület egy-egy olyan kicsi darabkája, amelyen a töltéssűrűség már jó közelítéssel állandónak tekinthető. Esetünkben, amikor a töltéseloszlás forgásszimmetrikus, a korongot kicsiny

Δ r

szélességű,

2 π r Δ r

területű körgyűrűkre érdemes felbontani, és így pl. a középső korong kilógó részének egy-egy oldalára jutó töltés:

\begin{matrix} q' = \sum_{r = R_{0}}^{R} η \cdot Δ A = \sum_{r = R_{0}}^{R} \frac{q}{2 π R \sqrt[]{R^{2} - r^{2}}} \cdot 2 π r Δ r . \end{matrix}

8. ábra

Ez a (nagyon bonyolultnak látszó) összeg meglepően egyszerűen kiszámítható, ha az összegzést nem az

r

változó, hanem az

y = \sqrt[]{R^{2} - r^{2}}

mennyiség szerint végezzük el. Az

y

távolság geometriai jelentése: az a magasság, ahonnan az 5. ábrán látható ,,vetítést'' végeztük. A 8. ábrán látható kicsiny körívet egyenes szakasznak tekintve, a megfelelő hasonló háromszögekből leolvashatjuk, hogy

\begin{matrix} \frac{Δ r}{Δ y} = \frac{y}{r}, \end{matrix}

továbbá azt, hogy az összegzési határoknak

y_{1} = 0

és

y_{2} = \sqrt[]{R^{2} - R_{0}^{2}}

felel meg. Így a keresett töltés:

\begin{matrix} q' = \sum_{r = R_{0}}^{R} \frac{q}{R y} r Δ r = \frac{q}{R} \sum_{y = y_{1}}^{y_{2}} \frac{1}{y} r \frac{y Δ y}{r} = \frac{q}{R} \sum_{y = y_{1}}^{y_{2}} Δ y = \frac{q}{R} (y_{2} - y_{1}), \end{matrix}

azaz

\begin{matrix} q' = q \sqrt[]{1 - \frac{R_{0}^{2}}{R^{2}}} . \end{matrix}

(3)

Ezzel egyenlő nagyságú töltés egyenletesen oszlik el a jobb oldali korong bal oldali felületén, tehát ott

\begin{matrix} η_{0} = \frac{q'}{R_{0}^{2} π} = \frac{q}{R_{0}^{2} π} \sqrt[]{1 - \frac{R_{0}^{2}}{R^{2}}} \end{matrix}

töltéssűrűséget alakít ki (síkkondenzátor). Emiatt (lásd a (2) képletet)

\begin{matrix} F_{balra} = 2 π k η_{0}^{2} \cdot R_{0}^{2} π = 2 k \frac{q^{2}}{R_{0}^{2}} (1 - \frac{R_{0}^{2}}{R^{2}}) \end{matrix}

(4)

erővel hat a jobb oldali korongra a tőle balra levő elekrosztatikus mező.
Kicsit bonyolultabb a korong jobb oldalán ható erő számítása. Az (1) és (2) összefüggések felhasználásával:

\begin{matrix} F_{jobbra} = 2 π k \sum_{a felületre}^{} η^{2} (r) \cdot Δ A = 2 π k \sum_{r = 0}^{R_{0}} \frac{q^{2}}{4 π^{2} R^{2}} \cdot \frac{1}{R^{2} - r^{2}} \cdot 2 π r Δ r . \end{matrix}

Itt is érdemes áttérni az

y

változó szerinti összegzésre:

\begin{matrix} F_{jobbra} = k \frac{q^{2}}{R^{2}} \sum_{y = \sqrt[]{R^{2} - R_{0}^{2}}}^{R} \frac{Δ y}{y} . \end{matrix}

Az integrálszámításban jártasak tudják, hogy a fenti összeg (az előtte álló szorzófaktor nélkül) az

f (y) = 1 / y

függvény grafikonja alatti

T

terület

y_{1} = \sqrt[]{R^{2} - R_{0}^{2}}

és

y_{2} = R

határok között:

\begin{matrix} \int_{\sqrt[]{R^{2} - R_{0}^{2}}}^{R} \frac{1}{y} d y, \end{matrix}

és ennek az integrálnak a nagysága

\begin{matrix} T = ln \frac{y_{2}}{y_{1}} = \frac{1}{2} ln \frac{R}{\sqrt[]{R^{2} - R_{0}^{2}}}, \end{matrix}

vagyis

\begin{matrix} F_{jobbra} = - \frac{k q^{2}}{2 R^{2}} ln (1 - \frac{R_{0}^{2}}{R^{2}}) . \end{matrix}

(5)

Egy kis matematikai kitérő. Az integrálszámítás formális szabályainak ismerete nélkül is ki lehet találni, hogy mennyi az

f (y) = 1 / y

függvény grafikonja alatti terület pl. az 1 és

a

határok között. Jelöljük ezt a mennyiséget

T (a)

-val!

9. ábra

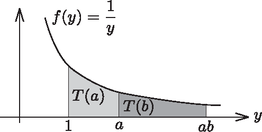A 9. ábráról leolvashatjuk, hogy a keresett kifejezés eleget tesz a

T (a) + T (b) = T (a b)

függvényegyenletnek. (Kihasználtuk, hogy ha az ábrán sötétebben jelölt tartományt a vízszintes tengely mentén

a

-ad részére zsugorítjuk, a függőleges tengely mentén pedig

a

-szorosára nyújtjuk, akkor sem a grafikon alakja, sem az alatta levő terület nem változik meg, tehát ez a terület éppen

T (b)

.)
A függvényegyenletből következik, hogy

\begin{matrix} T (e^{2}) = T (e \cdot e) = 2 \cdot T (e), és hasonlóan T (e^{n}) = n \cdot T (e), \end{matrix}

továbbá

\begin{matrix} T (\sqrt[m]{e}) + ... + T (\sqrt[m]{e}) = m \cdot T (\sqrt[m]{e}) = T (e), ahonnan T (e^{\frac{1}{m}}) = \frac{1}{m} \cdot T (e), \end{matrix}

és általában

\begin{matrix} T (e^{\frac{n}{m}}) = \frac{n}{m} T (e), \end{matrix}

vagyis minden racionális

x

-re (folytonos függvény esetén minden

x

-re)

\begin{matrix} T (e^{x}) = x \cdot T (e) = konstans \cdot x, azaz T (a) = konstans \cdot ln a . \end{matrix}

Mivel az 1-hez nagyon közeli

a

számokra

ln a \approx a - 1

(próbáljuk ki zsebszámológépen), és ilyen esetben a terület is jó közelítéssel

a - 1

, hiszen egy téglalap területeként számolható, a fenti képletben szereplő konstans számértéke 1 kell legyen.
Eszerint

T (a) = ln a

, és tetszőleges határok közé eső terület (a zsugorítás‐nyújtás módszerének alkalmazásával)

\begin{matrix} T (y_{1} < y < y_{2}) = T (\frac{y_{2}}{y_{1}}) = ln \frac{y_{2}}{y_{1}} . \end{matrix}

Az Eötvös-versenyben szereplő szélső korongra ható (4) és (5) erők eredője akkor válik nullává, ha a középső, semleges korong

R^{*}

sugarára teljesül:

\begin{matrix} F_{balra} - F_{jobbra} = k q^{2} [\frac{2}{R_{0}^{2}} (1 - \frac{R_{0}^{2}}{{R^{⋆}}^{2}}) + \frac{1}{2 {R^{⋆}}^{2}} ln (1 - \frac{R_{0}^{2}}{{R^{⋆}}^{2}})] = 0. \end{matrix}

Bevezetve az

\begin{matrix} \frac{{R^{⋆}}^{2}}{R_{0}^{2}} = λ \end{matrix}

jelölést, a korongok sugárarányának négyzetére a következő (logaritmikus) egyenletet kapjuk:

\begin{matrix} 2 (λ - 1) + \frac{1}{2} ln (1 - \frac{1}{λ}) = 0, \end{matrix}

amely numerikusan (akár még egy zsebszámológéppel is) megoldható. Az eredmény:

λ \approx 1, 34

, ahonnan

\begin{matrix} R^{⋆} \approx 1, 16 R_{0} . \end{matrix}

A semleges korongnak tehát mintegy 16 százalékkal nagyobb méretűnek kell lennie ahhoz, hogy éppen nullára csökkentse a két töltött fémkorong között ható erőt.

Gnädig Péter

¹A feladat teljes szövegét és a megoldást lásd a KöMal 2011. évi 3. számának 173. oldalán.

²A kicsiny felületdarabka nagyságát a magyar nyelvű szakirodalomban gyakran $Δ F$ -fel jelölik. Az angol nyelvű írásokban a $Δ A$ vagy $Δ S$ jelöléseket találjuk, ezek az area és a surface szavakra utalnak. A $Δ F$ jelölést akkor célszerű elkerülni, ha felmerül, hogy a képletekben a felület az általában ugyancsak $F$ -fel jelölt erővel összetéveszthető.

³Erre a tényre az Eötvös-verseny 3. feladatának kitűzője, Károlyházy Frigyes professzor hívta fel a cikk szerzőjének figyelmét.