Kezdőlap


Cím:	Fizika Világbajnokság válogató versenyének feladatai
Füzet:	2011/április, 233 - 244. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Töltött korongok. Két vékony, 5 cm sugarú fémkorongot szigetelő fonállal, egymással párhuzamosan felfüggesztünk (lásd 1.

a)

ábra). A korongok egymáshoz közel (mondjuk 2 mm-re) vannak.
1. Számítsuk ki a korongok között ható erőt, ha kicsiny

+ q

és

- q

töltéseket viszünk rájuk. Mivel

q

kicsi, a korongok elmozdulását és a kisülés lehetőségét nem kell figyelembe vennünk.
2. Ezután vizsgáljunk egyetlen korongot. Határozzuk meg a felületi töltéseloszlást egy

R

sugarú,

+ q

töltésű, magában álló fémkorongon (ez a töltéseloszlás hasznos lehet a következő kérdés megválaszolásához).
Ezután mindkét korongot

+ q

töltéssel látjuk el, majd egy harmadik,

R^{*} > 5

cm sugarú, semleges fémkorongot helyezünk a kettő közé egy szigetelő fonálon. A három korong egymással párhuzamos, középpontjaik pedig ugyanazon a vízszintes egyenesen fekszenek (síkjukra merőlegesen nézve tehát koncentrikus köröknek tűnnek). Ezt az állapotot mutatja az 1.

c)

ábra.
3. Mekkora a középső korong

R^{*}

sugara, ha a két szélső, töltött lemezre ható elektrosztatikus erő nulla? (Az élek hatását hanyagoljuk el a feladatban.)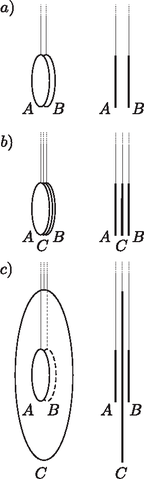

1. ábra

2. feladat. Henger ütközés. Egy

M

tömegű,

R

sugarú üreges henger nyugszik a vízszintes síkon. A henger belsejében egy

m

tömegű,

r

sugarú tömör korong található. Kezdetben a korong középpontja

l

távolságra van a henger középpontjától, és

y

-irányban mozog

v

sebességgel a 2. ábrán látható módon. Ha mást nem kötünk ki, minden ütközés rugalmas, és a súrlódás mindig elhanyagolható.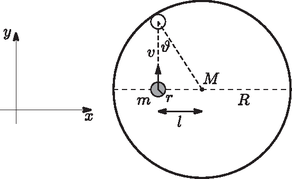

2. ábra

1. Határozzuk meg a korong és a henger sebességének

x

- és

y

-komponenseit közvetlenül az első ütközés után. A választ

m

M

v

és

ϑ

függvényében adjuk meg.
2. Határozzuk meg a korong és a henger sebességének

x

- és

y

-komponenseit közvetlenül a második ütközés után. A választ

m

M

v

és

ϑ

függvényében adjuk meg.
3. Ha kezdetben a korong helyzete

l = (R - r) / 2

, határozzuk meg a korong és a henger sebességének

x

- és

y

-komponenseit közvetlenül az

n

-edik ütközés után.
4. Milyen feltételnek kell

l

-re teljesülnie, hogy a korong az

n

-edik ütközés után

y

-irányú sebességgel mozogjon, és az

M

henger nyugalomban maradjon? Határozzuk meg a henger középpontjának két egymást követő nyugalmi helyzete közötti távolságot.
5. Ebben a részben a korong és a henger közötti súrlódás nem hanyagolható el. Az 1. részhez hasonlóan a henger nyugalomban van, a korong középpontja pedig

l < (R - r)

távolságra van a henger középpontjától, és

y

-irányú sebességgel mozog a 2. ábrán látható módon. Feltéve, hogy az ütközés folyamata során az érintkezési pont nem csúszik el, határozzuk meg a korong és a henger szögsebességét közvetlenül az első ütközés után.

3. feladat. Szigetelő hullámvezető lemez.
1. Teljes visszaverődés. Egy polarizált monokromatikus elektromágneses síkhullám elektromos tere általánosan

E (r, t) = E exp (k \cdot r - ω t)

alakban adható meg, ahol

E

a hullám amplitúdója,

k

a hullámszámvektor és

ω

a körfrekvencia. Tegyük fel, hogy egy

n_{1}

törésmutatójú közegben

ω

körfrekvenciájú monokromatikus síkhullám terjed, ami elér egy

n_{2}

törésmutatójú közeget. A bejövő hullám

ϑ_{i}

szöget zár be a határfelület beesési merőlegesével. A probléma során csak transzverzálisan polarizált hullámokkal foglalkozunk, azaz olyanokkal, amelyekben az elektromos mező merőleges a beesési síkra. Egyik közeg sem mágneses.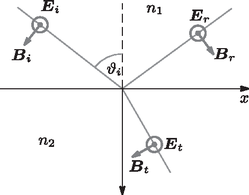

a)

ábra

1. Ha

n_{1} > n_{2}

, létezik egy

ϑ_{c}

határszög, amelyre teljesül, hogy a

ϑ_{i} > ϑ_{c}

szög alatt beérkező hullámok teljesen visszaverődnek (total internal reflection: TIR). A visszavert hullám fázisa

δ

-val késik a bejövőhöz képest. Vezessük le

δ

-t, és adjuk meg

n_{1}

n_{2}

, és

ϑ_{i}

függvényében.
2. A szükséges határfeltételek felhasználásával adjuk meg a visszaverődés

R

mértékét

n_{1} > n_{2}

esetén. Mutassuk meg, hogy a hullám teljesen visszaverődik minden

ϑ_{i} > ϑ_{c}

esetén.
2. Erősítő fáziscsatolás. A legegyszerűbb dielektromos hullámvezető egy

d

vastagságú,

n_{1}

törésmutatójú síklemez, amit homogén,

n_{2}

törésmutatójú közeg vesz körül (

n_{1} > n_{2}

). TIR esetén a lemez felhasználható hullámok veszteség nélküli továbbítására, feltéve, hogy a hullámok interferenciája erősítő, azaz a hullámfrontok megmaradnak a hullám terjedése során a hullámvezetőben. A hullámszámok vákuumban, az

n_{1}

és az

n_{2}

törésmutatójú közegben rendre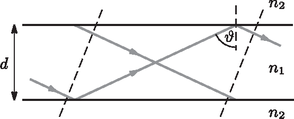

k_{0}

k_{1}

, és

k_{2}

b)

ábra

1. Határozzuk meg az erősítő fáziscsatolás szükséges feltételét.
2. A hullámot csak

ϑ

bizonyos értékei esetén lehet veszteségmentesen továbbítani. Mutassuk meg, hogy

ϑ

-nak ki kell elégítenie a következő egyenletet:

\begin{matrix} k_{1} d cos ϑ - δ = m π; m = 0,1,2, ... . \end{matrix}

(1)

Igazoljuk, hogy a fenti egyenlet így is felírható:

\begin{matrix} \sqrt[]{u^{2} + v^{2}} = \frac{k_{0} d}{2} \sqrt[]{n_{1}^{2} - n_{2}^{2}}, & (2) \\ u tan u = v vagy u cot u = v, & (3) \end{matrix}

u = \frac{k_{1} d}{2} cos ϑ

és

v = \frac{d}{2} \sqrt[]{k_{1}^{2} sin^{2} ϑ - k_{2}^{2}}

.
3. Maxwell-egyenletek. A Maxwell-féle hullámegyenlet egy

ε

relatív dielektromos állandójú közegben az elektromos térerősségre:

\begin{matrix} (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}) E (r, t) = ε ε_{0} μ_{0} \frac{\partial^{2} E (r, t)}{\partial t^{2}} . \end{matrix}

(4)

A 3.

c)

ábrán látható hullámvezető lemez esetén

ε = n_{1}^{2}

, ha

0 < z < d

, különben pedig

ε = n_{2}^{2}

. Olyan koordinátarendszerben, amelyben a hullám az

x z

-síkban terjed, az elektromos térerősség általánosan

\begin{matrix} E (r, t) = E (x, z, t) = E (z) exp (i (β x - ω t)) \end{matrix}

(5)

alakban adható meg, ahol

β

az effektív terjedési állandó a hullámvezetőben, figyelembe véve a rendszer eltolási szimmetriáját az

x

-tengely irányában. A transzverzálisan polarizált hullámok továbbítása esetén

E (z)

y

-irányú, továbbá

E (r, t)

-nek egyszerű harmonikus rezgésnek kell lennie a rétegen belül, azon kívül pedig exponenciálisan kell lecsengenie.

c)

ábra

1. Mi a kapcsolat

β

k_{1}

és

ϑ

között?
2. A

z = 0

és

z = d

értéknél felírható határfeltételek felhasználásával vezessük le a hullámvezetés 2. részben megkapott feltételét a Maxwell-egyenletekből.
4. Normál módusok. A normál módusok

ϑ

azon értékeihez kötődnek, amikor a lemezben hullámvezetés történik. Az

m = 0

-hoz (lásd 2. rész) tartozó módus az alapmódus (legalacsonyabb módus, első módus), az

m = 1

-hez tartozó módus a második módus stb.
1. Vázoljunk fel az

(u, v)

koordinátarendszerben a (2) és a (3) egyenleteket leíró görbéket. Határozzuk meg annak szükséges feltételét, hogy csak egy normál módus létezzen.
2. Mutassuk meg, hogy a szigetelő lemez által támogatott módusok maximális száma

\begin{matrix} M = ⌈ \frac{k_{0} d}{π} \sqrt[]{n_{1}^{2} - n_{2}^{2}} ⌉, \end{matrix}

(6)

ahol

⌈ x ⌉

azt a legkisebb egész számot jelöli, amely legalább akkora, mint

x

.
3. Igazoljuk, hogy a körfrekvencia minden

\begin{matrix} Δ ω = \frac{π c}{d \sqrt[]{n_{1}^{2} - n_{2}^{2}}} \end{matrix}

(7)

emelkedése a módusok számát eggyel növeli.
4. Az (1) egyenlet alapján mutassuk meg, hogy a csoportsebesség (

\partial ω / \partial β

) minden támogatott normál módusra

\begin{matrix} v_{g} = \frac{d tan ϑ + \frac{\partial δ}{\partial β}}{\frac{n_{1} d}{c cos ϑ} - \frac{\partial δ}{\partial ω}} . \end{matrix}

(8)

5. Mutassuk meg, hogy az

L

távolság befutásához szükséges idők közötti legnagyobb időkülönbség a különböző módusokban terjedő hullámok esetén

\begin{matrix} τ = \frac{L}{c} (n_{1} - n_{2}) . \end{matrix}

(9)

6. Legyen

n_{1} = 1, 7

;

n_{2} = 1, 5

;

λ = 800

nm (vákuumban) és

d = 1 μ m

. Határozzuk meg az összes módust

ϑ > ϑ_{c}

-re. Ábrázoljuk az

E (z)

elektromos térerősséget ezekre a módusokra.

4. feladat. Mágneses dipólus rezgése. Egy

m_{1}

mágneses nyomatékkal rendelkező dipólust helyezünk az origóba, melynek mágnesesnyomaték-vektora a

+ x

irányba mutat.
1. Határozzuk meg a mágneses indukciót a tér minden pontjában.
2. Egy másik dipólust helyezünk az origótól

r

távolságra, ennek helyvektora

ϑ

szöget zár be az

x

-tengellyel. A második dipólus

m_{2}

mágneses nyomatéka

α

szöget zár be az

x

-tengellyel. Az elrendezés a 4. ábrán látható. Határozzuk meg a második dipólusra ható forgatónyomatékot.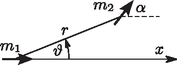

4. ábra

3. Határozzuk meg a két dipólus közti kölcsönhatási energiát.
4. Határozzuk meg a második dipólusra ható erőt.
5. A két dipólust egy elhanyagolható tömegű fonállal összekötjük úgy, hogy a kettő távolsága

r

maradjon. Míg az első dipólus helye és iránya rögzített, a második szabadon mozoghat (

r

távolságban) az ábra síkjában, és irányítottsága is szabadon változhat. Írjuk fel a második dipólus mozgásegyenletét. A második dipólus tömege és tehetetlenségi nyomatéka rendre

m

és

I

.
6. Kezdetben a második dipólus rögzítve van az

x

-tengelyen, a mágneses nyomatéka

α_{0} ≪ 1

szöget zár be az

x

-tengellyel. A második dipólus rögzítését

t = 0

-kor feloldjuk. Írjuk fel a második dipólus mozgásegyenletét, figyelembe véve, hogy

ϑ

és

α

kicsi. Legyen

I = m r^{2} / 5

.
7. A rendszer harmonikus rezgést végez. Határozzuk meg a rezgés normál módusainak frekvenciáit. A rendszer normál módusban van, ha a rezgés paraméterei fázisban vannak, azaz így írhatók fel:

ϑ = ϑ_{0} cos (ω t + φ)

és

α = α_{0} cos (ω t + φ)

ω

-nak két lehetséges értéke van (jelölje ezeket

ω_{1}

és

ω_{2}

). Határozzuk meg

ω_{1}

és

ω_{2}

értékét.
8. Az egyes normál módusokra határozzuk meg

α

és

ϑ

amplitúdóinak hányadosát,

c_{1} = α_{1} / ϑ_{1}

-et és

c_{2} = α_{2} / ϑ_{2}

-t.
9. A rendszert a következő összefüggések írják le:

\begin{matrix} ϑ & = ϑ_{1} cos (ω_{1} t + φ_{1}) + ϑ_{2} cos (ω_{2} t + φ_{2}); \\ α & = c_{1} ϑ_{1} cos (ω_{1} t + φ_{1}) + c_{2} ϑ_{2} cos (ω_{2} t + φ_{2}) . \end{matrix}

A kezdeti feltételek felhasználásával határozzuk meg

ϑ_{1}

φ_{1}

ϑ_{2}

és

φ_{2}

értékét.

5. feladat. Csavaros kötél. Két egyforma,

m

tömegű fémcsíkot egy nagy, súrlódásmentes hengerre helyezünk. A csíkokat két rugalmas kötéllel kötjük össze, úgy, hogy a kötelek nyújtatlanok és párhuzamosak egymással. A kötelek rugóállandója

k

és követik a Hooke-törvényt. A kötelek rögzítési pontja mindkét csíkon egy átmérő két végpontján van. Az így kapott eszközt az 5. ábra mutatja. Az

A

csíkot a hengerre csavarozzuk, míg a

B

csík szabadon mozoghat és foroghat a henger tengelye körül.
1. A hengert függőleges helyzetbe állítjuk állandó

g

nehézségi erőtérben úgy, hogy az

A

csík a

B

csík fölé kerüljön. A

B

csíkot ezután

N

-szer körbeforgatjuk, a két csík közti távolságot

x_{0}

értéken tartva. Ezután a

B

csík forgását meggátoljuk egy csavarral, ahogy az 5. ábrán láthatjuk.

5. ábra. Az eszköz kezdeti elrendezésében. A csavar a

B

csík forgásának meggátlására használható

a)

Adjunk meg egy olyan egyenletet, amelyből a paraméterek numerikus értékeinek ismeretében

x_{1}

, az új egyensúlyi helyzet meghatározható.

b)

Bizonyos feltételek mellett a fémcsík harmonikus rezgést végez. Határozzuk meg a kis

Δ x

amplitúdójú rezgések frekvenciáját

k

r

N

x_{0}

és

x_{1}

függvényében.
2. A hengert újra vízszintes helyzetbe hozzuk, a köteleket visszaállítjuk eredeti állapotukba, és a forgását megakadályozzuk a csavarral.

a)

B

csíkra

F

vízszintes feszítőerővel hatunk. Ha az erőt nagyon lassan, fokozatosan növeljük, a kötelek

F_{0}

erőnél szakadnak el. Mekkora a legkisebb minimális állandó erő, amely a kötelek elszakításához szükséges?

b)

B

csíkot a rögzítés előtt

N

-szer körbeforgatjuk, a köteleket nyújtatlanul tartva. Határozzuk meg a kötelek elszakításához szükséges minimális erőt, ha az erőt

(i)

nagyon lassan növeljük,

(i i)

állandó értéken tartjuk.
3. A rendszer eredeti vízszintes helyzetében van. A

B

csík rögzítését feloldjuk és

ϑ_{0}

szöggel elforgatjuk, miközben a két csík távolsága

x_{0}

marad, majd elengedjük (kezdetben

\dot{x} (0) = 0

és

\dot{ϑ} (0) = 0

a)

Írjuk fel a

B

csík mozgásegyenletét.

b)

Oldjuk meg a mozgásegyenletet

x (t)

-re és

ϑ (t)

-re.

c)

Adjuk meg a maximális sebességet és szögsebességet, valamint a csíkok összeütközéséig eltelő

T

időt.

6. feladat. Folyékony levegő. Oxigén és nitrogén keverékét tartjuk egy zárt, egyik végén dugattyúval ellátott tartályban állandó

T = 77, 4

K hőmérsékleten. A gázkeverék teljes anyagmennyisége 1,1 mol, kezdeti nyomása 0,5 atm. A dugattyú segítségével a gázkeveréket állandó hőmérsékleten lassan összenyomjuk.
Elfogadható közelítésekkel élve ábrázoljuk a rendszer nyomását a térfogat függvényében a kezdeti térfogat tizedéig, ha az oxigén és a nitrogén anyagmennyiségének aránya

(n_{O_{2}} / n_{N_{2}})

(a)

1/9;

(b)

2/9;

(c)

1/4.
Határozzuk meg a nyomás és a térfogat értékét ezen izotermák jellegzetes pontjaiban.
A következő adatok állnak rendelkezésünkre:
‐ 1 atm nyomáson a folyékony nitrogén forráspontja: 77,4 K;
‐ 1 atm nyomáson a folyékony oxigén forráspontja: 90,2 K;
‐ az oxigén párolgáshője: 213 J/g.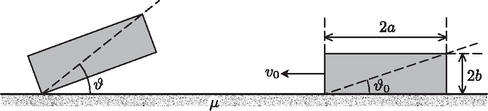

7. feladat. Csúszó hasáb. Egy

2 b

magasságú,

2 a

hosszúságú,

M

tömegű, téglatest alakú hasáb nyugszik érdes talajon, ahol a csúszási súrlódási együttható

μ

. A hasábot egy erős ütéssel mozgásba hozzuk úgy, hogy az hirtelen

v_{0}

vízszintes sebességet kap. Bizonyos körülmények között a hasáb hátsó vége felemelkedik és a hasáb forogni is fog az alsó elülső éle körül, ami a talajon marad.

a)

ábra. A hasáb, miután megkapta kezdeti sebességét

1. Vezessük le a hasáb forgómozgásának egyenletét

θ

a

b

μ

és

g

függvényében.
2. Adjuk meg azt a feltételt, nevesül

μ

értékét, ami lehetővé teszi a fentiek bekövetkezését.
A következő kérdésnél feltesszük, hogy a fenti feltétel teljesül.
3. Tekintsünk egy végállapotot, ahol a hasáb nyugalomban marad a 6.

b)

ábrán látható helyzetben, miután a tömegközéppontja

x

-szel mozdult el kezdeti helyzetétől. Lehetséges-e egy ilyen végállapot? Ha igen, számítsuk ki az eléréséhez szükséges kezdeti sebességet az alábbi adatokkal: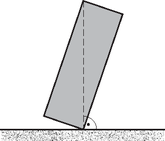

a = 0, 8

b = 1, 0

μ = 0, 9

;

x = 1, 65

{\dot{θ}}_{{max}_{}^{}} = 1, 27 s^{- 1}

b)

ábra. A hasáb kívánt végállapota

Megjegyzés:

a

b

és

μ

ismeretében a kezdeti sebesség numerikusan kiszámítható.

8. feladat. ,,Rugó és tömeg'' probléma. 1. Egy

M

tömegű test mozog egy félvégtelen rugó felé

v_{0}

kezdősebességgel a 7. ábrán látható módon. A rugó egységnyi hosszra eső tömege

μ

, rugóállandója szorozva a rugóhosszal pedig

K = k L

. A test és a rugó az

x = 0

helyen

t = 0

-kor ütközik. Adjuk meg a test sebességét az ütközés után mind az idő, mind a hely függvényében.

7. ábra

2. Ebben a feladatban egy másik,

m

tömegű testet helyezünk a rugó másik végére. Mennyi idő telik el az

M

tömegű test által kiváltott hullámfront

m

-hez való megérkezésétől a rugó és az

m

tömegű test szétválásáig? Számítsuk ki az

m

tömegű test sebességét is, amikor az elhagyja a rugót. Tegyük fel, hogy a rugóban a hullámok terjedési sebessége nagyobb

v_{0}

-nál, valamint a rugó elég hosszú ahhoz, hogy az

m

tömegű test leválásakor a visszavert hullámok még ne érjék el az

M

tömegű testet.

9. feladat. Két szilárd tárgy ütközési modellje. Két szilárd tárgy ütközésekor a mechanikai energiavesztés egyik módja a két test belsejében elinduló hanghullámok által felemésztett energia. Habár a valódi helyzet sokkal bonyolultabb, használjuk most a következő egyszerű modellt. Először helyettesítsük a szilárd rudakat egy-egy rugóval, melyek nyújtatlan hossza rendre

L_{l}

és

L_{r}

. A rugóállandó szorozva a rugóhosszal az egyes rugókra

K_{l}

és

K_{r}

; az egységnyi rugóhosszra eső tömeg pedig rendre

ϱ_{l}

és

ϱ_{r}

. Az

l

és

r

indexek a bal és jobb (left, right) oldali rugókat jelölik.
A bal oldali rugó

+ v_{0} / 2

, a jobb oldali pedig az ellenkező irányba

- v_{0} / 2

sebességgel halad. A rugók kezdetben nyújtatlanok.

t = 0

-kor a rugók az

x = 0

helyen ütköznek. A rugók egyes pontjainak elmozdulását az

y (x, t)

függvény írja le, tehát az ütközés után az eredetileg

x

koordinátájú pont a

t

időpontban az

x + y (x, t)

koordinátájú pontba kerül.
1. Vezessük le a rugók hullámegyenletét és adjuk meg a rugókban a hullámsebességet.
A hullámegyenlet általános megoldása

y (x, t) = ψ (c t - x) + φ (c t + x)

alakú, ahol

c

a hullám terjedési sebessége. A

ψ

és

φ

függvények alakját a határfeltételekből kaphatjuk meg.
2. Írjuk fel a határfeltételeket az

x = 0

x = - L_{l}

x = L_{r}

pontokban.
3. Írjuk fel az

y (x, t)

függvényt az ütközés előtt (

t \leq 0

), azaz az

y_{0, l} (x, t)

és

y_{0, r} (x, t)

függvényeket.

t = 0

-kor akusztikus hullám indul el mindkét rugóban az

x = 0

ütközési pontból. A rendszer dinamikáját a 8. ábrán látható hely-idő diagramon elemezzük. A vízszintes tengely az időt, a függőleges a rugó pontjainak helyzetét mutatja. A diagram minden vonala egy akusztikus hullámfrontot ábrázol, amelyek mindig akkor indulnak el, amikor egy hullám a határhoz érkezik.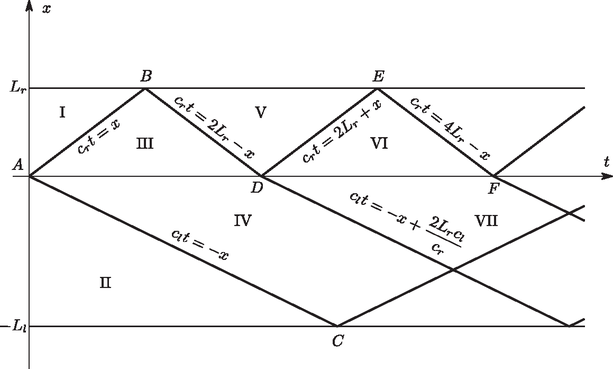

8. ábra. Hely‐idő diagram

Például az

A B

vonal az ütközéskor az

A

pontból kiinduló hullámfront helyzetét ábrázolja az idő függvényében. Írják le az

f_{l} (c_{l} t + x)

és

f_{r} (c_{r} t - x)

függvények az ütközéskor rendre a bal, illetve a jobb oldali rugóban elinduló hullámokat, ahol

c_{l}

és

c_{r}

rendre a bal és a jobb oldali rugókban terjedő hullám sebessége. A hely-idő diagramról látható, hogy a feladatban

L_{l} / c_{l} > L_{r} / c_{r}

. Amikor az

f_{r} (c_{r} t - x)

hullámfront eléri a

B

pontot, egy új

g_{r} (c_{r} t + x)

visszavert hullám indul visszafelé. Hasonló játszódik le a bal oldali rugóban a

C

pontban.
Amikor a jobb oldali rugóban a

g_{r} (c_{r} t + x)

hullámfront eléri a rugó végét (

D

pont az ábrán), egy új visszavert

(h_{r} (c_{r} t - x))

és egy új átvitt

(h_{l} (c_{l} t + x))

hullám indul el.
Ezek a jelenségek mindig bekövetkeznek, amikor egy hullámfront a két rugó valamelyik határára ér.
4. Írjuk fel az

y (x, t)

hullámfüggvényt a diagram I, II, III, IV, V, VI és VII jelű tartományaiban

y_{0}

f_{r}

f_{l}

g_{r}

h_{r}

és

h_{l}

segítségével.
5. A határfeltétel(ek) felhasználásával határozzuk meg az

f_{l} (c_{l} t + x)

és

f_{r} (c_{r} t - x)

függvényeket a rugók paramétereinek és kezdősebességének függvényében.
6. Határozzuk meg az érintkezési pont sebességét közvetlenül az első ütközés után.
7. A határfeltétel(ek) felhasználásával határozzuk meg a

g_{r} (c_{r} t + x)

függvényt a rugók paramétereinek és kezdősebességének függvényében.
Tekintsük azt az esetet, amikor a két rugó a hosszuktól eltekintve egyforma, azaz legyen

ϱ_{l} = ϱ_{r} = ϱ

és

K_{l} = K_{r} = K

. Legyen

L_{r} < L_{l}

.
8. Határozzuk meg

y (x, t)

-t a III és a IV tartományban. Ábrázoljuk

y (x)

-et

t = 0, 4 L / c

-nél. A grafikon rajzolásához legyen

L_{r} = 0, 6 L

L_{l} = L

és

v_{0} = 0, 5 c

.
9. Határozzuk meg

y (x, t)

-t az V tartományban. Ábrázoljuk

y (x)

-et

t = 0, 8 L / c

-nél,

L_{r}

L_{l}

és

v_{0}

az előző feladatban adott értékei mellett.
10. Mikor válik el egymástól a két rugó? Ábrázoljuk

y (x)

-et,

L_{r}

L_{l}

és

v_{0}

az előző feladatban adott értékei mellett.
11. Határozzuk meg a rugók ütközésére jellemző

e

ütközési számot.
12. Számítsuk ki a rugók ütközés utáni és előtti összes haladó mozgási energiájának hányadosát.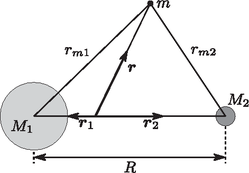

10. feladat. Lagrange-pontok stabilitása. A Földdel együtt a Nap körül forgó vonatkoztatási rendszerben öt egyensúlyi helyzet létezik (ahol a testekre ható eredő erő zérus). Ezt az öt pontot Lagrange-pontnak nevezzük Joseph Lagrange után, aki először tanulmányozta a háromtest-probléma ezen esetét. A rendszer teljesen precíz elemzése rendkívül bonyolult és kaotikus. Ebben a feladatban a két test tömege (

M_{1}

és

M_{2}

) sokkal nagyobb a harmadik testénél (

m

). Az

M_{1}

és

M_{2}

közti távolság legyen

R

9. ábra

1. A rendszer alapegyenletei

a)

Írjuk fel az

m

-re ható eredő gravitációs erő

F_{g}

vektorát.

b)

Feltéve, hogy

M_{1} > M_{2} ≫ m

, határozzuk meg az

M_{1}

‐

M_{2}

rendszer

Ω

szögsebességét.

c)

A rendszerrel együtt forgó vonatkoztatási rendszerben

m

-re ható tehetetlenségi erők lépnek fel. Írjuk fel az

m

-re ható eredő erő

F_{Ω}

vektorát ebben a vonatkoztatási rendszerben.

d)

Tekintsünk egy olyan koordinátarendszert, amelyben a három test az

x y

-síkban van, az

Ω

szögsebesség pedig

+ z

irányú. Az origót helyezzük az

x

tengelyen elhelyezkedő

M_{1}

‐

M_{2}

rendszer tömegközéppontjába. Írjuk

m

helyzetét

r = x (t) i + y (t) j

alakba. A forgó vonatkoztatási rendszerben írjuk fel az

m

-re ható eredő erőket, ha annak sebessége zérus. Használjuk az

α = \frac{M_{2}}{M_{1} + M_{2}}

és

β = \frac{M_{1}}{M_{1} + M_{2}}

paramétereket.
2. A Lagrange-pontok meghatározása. Öt olyan pont van a vonatkoztatási rendszerben, amelyekben az

m

-re ható eredő erő zérus. Ezek közül három (

L_{1}

L_{2}

L_{3}

) az

M_{1} M_{2}

egyenesen (az

x

-tengelyen), míg kettő az

x y

-síkon szimmetrikus helyzetben van az

x

-tengely alatt és fölött, azaz

y_{4} = - y_{5}

a)

Először

L_{1}

L_{2}

és

L_{3}

meghatározását végezzük el. Legyen

x = (ν - α) R

, ahol

ν

jelenti

m

és

M_{1}

távolságát

R

egységben. Írjunk fel egy olyan egyenletet, amit ezeknek a pontoknak ki kell elégítenie. Az egyenletet

ν

-vel és

α

-val fejezzük ki.

b)

Az egyenlet három esetre bomlik (ezek adják az egyes Lagrange-pontokat):

ν < a

a < ν < b

, és

b < ν

. Határozzuk meg

a

és

b

értékét.
A továbbiakban feltesszük, hogy

α

kicsi (a Nap-Föld rendszerben ez

3, 0 \cdot 10^{- 6}

α

-val csak a legkisebb nem-nulla rendben számolunk, a magasabb rendű tagokat elhanyagoljuk. A következő kérdések segítenek az

x

-tengelyen fekvő Lagrange-pontok meghatározásában.

c)

Az első esetben (

ν < a

) legyen

ν = - 1 + δ_{1}

, ahol

δ_{1}

egy

α

-tól függő kicsiny pozitív szám.

ν

ezen értéke az

L_{1}

Lagrange-pont helyzetét

x = - R (1 + ζ_{1})

alakban adja meg. Határozzuk meg

ζ_{1}

-et

α

függvényében.

d)

A második esetben (

a < ν < b

) legyen

ν = 1 - δ_{2}

, ahol

δ_{2}

egy

α

-tól függő kicsiny pozitív szám.

ν

ezen értéke az

L_{2}

Lagrange-pont helyzetét

x = R (1 - ζ_{2})

alakban adja meg. Határozzuk meg

ζ_{2}

-t

α

függvényében.

e)

A harmadik esetben (

b < ν

) legyen

ν = 1 + δ_{3}

, ahol

δ_{3}

egy

α

-tól függő kicsiny pozitív szám.

ν

ezen értéke az

L_{3}

Lagrange-pont helyzetét

x = R (1 + ζ_{3})

alakban adja meg. Határozzuk meg

ζ_{3}

-at

α

függvényében.
A negyedik és ötödik Lagrange-pont helyzetének meghatározása összetettebb módszert igényel. Először bontsuk fel az

m

-re ható erőt az

r

vektorral párhuzamos és merőleges komponensre.

f)

Adjuk meg az

r

vektorral párhuzamos

{\hat{e}}_{∥}

és a rá merőleges

{\hat{e}}_{⊥}

egységvektort az

x y

-síkban.

g)

Határozzuk meg az

m

-re ható eredő erő

r

-rel párhuzamos

F_{Ω}^{∥}

és a rá merőleges

F_{ω}^{⊥}

komponensét.

h)

Adjuk meg az

r

-re merőleges irányú egyensúly feltételét. Ennek felhasználásával adjuk meg az

r_{m 1}

és

r_{m 2}

közötti kapcsolatot.

i)

Adjuk meg az

r

-rel párhuzamos irányú egyensúly feltételét. Ennek felhasználásával adjuk meg az

r_{m 1}

és

R

közötti kapcsolatot.

j)

Határozzuk meg a negyedik és az ötödik Lagrange-pont helyzetét, rendre

(x_{4}, y_{4})

-et és

(x_{5}, y_{5})

-öt.
3. A Lagrange-pontok stabilitása. Az egyes Lagrange-pontok stabilitásának ellenőrzésére megzavarjuk

m

-et egyensúlyi helyzetében. Mivel ebben a rendszerben az erők

m

(x, y)

helyétől és

(v_{x}, v_{y})

sebességétől függnek, a stabilizáló erőket a helyzet és a sebesség különböző változásaira kell kiszámítani. Fejezzük ki az erőt az alábbi módon:

\begin{matrix} F_{x} & (x_{0} + δ x, y_{0} + δ y, v_{x,0} + δ v_{x}, v_{y,0} + δ v_{y}) = \\ = \frac{\partial F_{x}}{\partial x} δ x + \frac{\partial F_{x}}{\partial y} δ y + \frac{\partial F_{x}}{\partial v_{x}} δ v_{x} + \frac{\partial F_{x}}{\partial v_{y}} δ v_{y}; \\ F_{y} & (x_{0} + δ x, y_{0} + δ y, v_{x,0} + δ v_{x}, v_{y,0} + δ v_{y}) = \\ = \frac{\partial F_{y}}{\partial x} δ x + \frac{\partial F_{y}}{\partial y} δ y + \frac{\partial F_{y}}{\partial v_{x}} δ v_{x} + \frac{\partial F_{y}}{\partial v_{y}} δ v_{y} . \end{matrix}

Ez az erő figyelembe veszi az m tömeg sebességének járulékát. Az összes parciális deriváltat az egyensúlyi helyzetben (

x_{0}

y_{0}

v_{x,0}

v_{y,0}

) számítjuk ki.

a)

Adjuk meg

\frac{1}{m} \frac{\partial F_{x}}{\partial x}

\frac{1}{m} \frac{\partial F_{x}}{\partial y}

\frac{1}{m} \frac{\partial F_{y}}{\partial x}

\frac{1}{m} \frac{\partial F_{y}}{\partial y}

általános alakját. Mutassuk meg, hogy

\frac{\partial F_{x}}{\partial y} = \frac{\partial F_{y}}{\partial x}

b)

Számítsuk ki

\frac{1}{m} \frac{\partial F_{x}}{\partial v_{x}}

-et,

\frac{1}{m} \frac{\partial F_{x}}{\partial v_{y}}

-t,

\frac{1}{m} \frac{\partial F_{y}}{\partial v_{x}}

-et, és

\frac{1}{m} \frac{\partial F_{y}}{\partial v_{y}}

-t.
A fenti nyolc együtthatónak a rugóállandó analógiájára a zavarokat csillapítania kell. Ezek után ellenőrizzük az öt Lagrange-pont stabilitását.

α

-val csak a legkisebb nem-nulla rendben számoljunk, hanyagoljuk el a magasabb rendű tagokat.

c)

Az első Lagrange-pont

(i)

Mutassuk meg, hogy

\frac{1}{m} \frac{\partial F_{x}}{\partial x} = c_{1} Ω^{2}

, és határozzuk meg

c_{1}

-et.

(i i)

Mutassuk meg, hogy

\frac{\partial F_{x}}{\partial y} = \frac{\partial F_{y}}{\partial x} = 0

(i i i)

Mutassuk meg, hogy

\frac{1}{m} \frac{\partial F_{y}}{\partial y} = c_{2} α Ω^{2}

, és határozzuk meg

c_{2}

-t.

(i v)

δ x = A e^{λ t}

és

δ y = B e^{λ t}

(

A, B \neq 0

) helyettesítésével határozzuk meg

λ

-t, kizárólag

α

és

Ω

függvényében.

(v)

λ

-nak négy lehetséges értéke van. Adjuk meg azt a feltételt, amit ezeknek a megoldásoknak teljesíteniük kell, hogy

L_{1}

stabil legyen, és döntsük el, hogy

L_{1}

stabil-e.

(v i)

A Nap‐Föld rendszerre

α = 3, 0 \cdot 10^{- 6}

, és

Ω = 2 π

/év. Ha ez a pont stabil, adjuk meg a körülötte végezhető rezgés periódusidejét (nap mértékegységben), ha nem stabil, akkor az

1 / λ

időállandót (szintén napokban).

d)

A második Lagrange-pont

(i)

Mutassuk meg, hogy

\frac{1}{m} \frac{\partial F_{x}}{\partial x} = c_{3} Ω^{2}

, és határozzuk meg

c_{3}

-at.

(i i)

Mutassuk meg, hogy

\frac{\partial F_{x}}{\partial y} = \frac{\partial F_{y}}{\partial x} = 0

(i i i)

Mutassuk meg, hogy

\frac{1}{m} \frac{\partial F_{y}}{\partial y} = c_{4} Ω^{2}

, és határozzuk meg

c_{4}

-et.

(i v)

δ x = A e^{λ t}

és

δ y = B e^{λ t}

(

A, B \neq 0

) helyettesítésével határozzuk meg

λ

-t, kizárólag

α

és

Ω

függvényében.

(v)

λ

-nak négy lehetséges értéke van. Adjuk meg azt a feltételt, amit ezeknek a megoldásoknak teljesíteniük kell, hogy

L_{2}

stabil legyen, és döntsük el, hogy

L_{2}

stabil-e.

(v i)

Ha ez a pont a Nap‐Föld rendszerben stabil, adjuk meg a körülötte végezhető rezgés periódusidejét (nap mértékegységben), ha nem stabil, akkor az

1 / λ

időállandót (szintén napokban).
A harmadik Lagrange-pont hasonló a másodikhoz, tehát nem kell külön foglalkoznunk vele.

e)

A negyedik Lagrange-pont

(i)

Mutassuk meg, hogy

\frac{1}{m} \frac{\partial F_{x}}{\partial x} = c_{5} Ω^{2}

, és határozzuk meg

c_{5}

-öt.

(i i)

Mutassuk meg, hogy

\frac{1}{m} \frac{\partial F_{x}}{\partial y} = \frac{1}{m} \frac{\partial F_{y}}{\partial x} = (c_{6} + c_{7} α) Ω^{2}

, és határozzuk meg

c_{6}

-ot és

c_{7}

-et.

(i i i)

Mutassuk meg, hogy

\frac{1}{m} \frac{\partial F_{y}}{\partial y} = c_{8} Ω^{2}

, és határozzuk meg

c_{8}

-at.

(i v)

δ x = A e^{λ t}

és

δ y = B e^{λ t}

(

A, B \neq 0

) helyettesítésével határozzuk meg

λ

-t, kizárólag

α

és

Ω

függvényében.

(v)

Legyen

ζ = M_{1} / M_{2}

. Határozzuk meg

ζ

azon értéktartományát, amire a negyedik Lagrange-pont stabil.
Az ötödik Lagrange-pont azonosan viselkedik, mint a negyedik, így nem kell külön foglalkoznunk vele.

¹A versenyről részletes információ található a KöMaL honlapján (lásd Aktuális/WoPhO).
A feladatokat angolból fordította: Szabó Attila.
A megoldások beküldési határideje: 2011. június 30.