Kezdőlap


Cím:	A 41. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Honyek Gyula , Tasnádi Tamás
Füzet:	2010/október, 422 - 438. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 41. Nemzetközi Fizikai Diákolimpia feladatainak megoldása¹

Elméleti feladatok

1. feladat. Tükörtöltés egy fémtárgyban

1. részfeladat.

a)

Mekkora az elektromos potenciál értéke a gömbön?
Mivel a gömb földelt, az elektromos potenciál a felszínén zérus.

b)

A tükörtöltés

q'

nagyságának és

r'

helyzetének meghatározása.
A feladat nem követeli meg a tükörtöltés módszerének igazolását, csupán a tükörtöltés nagyságának és helyzetének meghatározását kéri a módszer ismeretében. E két paraméter meghatározásához elegendő, ha a gömb két különböző pontjában előírjuk, hogy az elektromos potenciál legyen zérus. Célszerű a két töltés egyenesén fekvő

G

és

H

pontot választani (1. ábra):

\begin{matrix} Φ_{G} & = \frac{1}{4 π ε_{0}} (\frac{q}{d - R} + \frac{q'}{R - d'}) = 0, \\ Φ_{H} & = \frac{1}{4 π ε_{0}} (\frac{q}{d + R} + \frac{q'}{d' + R}) = 0. \end{matrix}

Egyszerűen adódik, hogy az egyenletrendszer megoldása

q'

-re és

d'

-re:

\begin{matrix} q' = - q \frac{R}{d}, d' = \frac{R^{2}}{d} . \end{matrix}

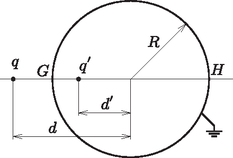1. ábra. A töltés, a tükörtöltés és a földelt fémgömb

Megjegyzés. A kapott eredményhez két elemi geometriai tétel is kapcsolódik. Egyrészt, mivel

d d' = R^{2}

, a töltést és a tükörtöltést egy olyan inverzió (gömbi tükrözés) viszi át egymásba, melynek alapgömbje a földelt fémgömb. Másrészt, az a tény, hogy a két töltés eredő potenciálja a gömbön nulla, azt jelenti, hogy a gömb pontjainak a két töltéstől mért távolságaránya állandó, tehát a gömb a két töltéshez tartozó Apollóniusz-gömb.

c)

Mekkora erő hat a

q

töltésre?
Minthogy a fémgömb elektromos tere a gömbön kívül megegyezik a

q'

tükörtöltés terével, a gömb és a

q

töltés közti erő megegyezik a

q

és

q'

töltések között ható Coulomb-erővel:

\begin{matrix} F = \frac{1}{4 π ε_{0}} \frac{q \cdot | q' |}{{(d - d')}^{2}} = \frac{1}{4 π ε_{0}} \frac{q^{2} R d}{{(d^{2} - R^{2})}^{2}} . \end{matrix}

Mivel

q

és

q'

ellentétes előjelűek, ezért a köztük ható

F

erő vonzó.

2. részfeladat.

a)

Mekkora az

A

pontban az elektromos térerősségvektor?

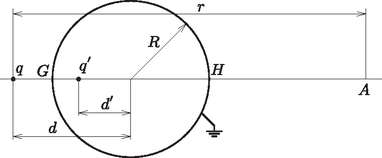2. ábra. Az

A

pontban a földelt gömb részlegesen leárnyékolja az elektromos teret

A földelt gömb hatását helyettesíthetjük a

q'

tükörtöltéssel, így az elektromos tér két ponttöltés terének eredőjeként adódik:

\begin{matrix} E_{A} = \frac{1}{4 π ε_{0}} (\frac{q}{r^{2}} - \frac{q'}{{(r - d + d')}^{2}}) e_{A} = \frac{q}{4 π ε_{0}} (\frac{1}{r^{2}} - \frac{R d}{{(r d + R^{2} - d^{2})}^{2}}) e_{A}, \end{matrix}

ahol

e_{A}

q

töltéstől

A

-ba mutató egységvektor.

b)

Hogyan közelíthető ez a formula, ha

r ≫ d

?
Ha

r ≫ d

, akkor az előző formula második tagja:

\begin{matrix} \frac{R d}{{(r d + R^{2} - d^{2})}^{2}} = \frac{R}{r^{2} d} {(1 - \frac{d}{r} + \frac{R^{2}}{r d})}^{- 2} \approx \frac{R}{r^{2} d} (1 + \frac{2 d}{r} - \frac{2 R^{2}}{r d}) . \end{matrix}

Ezt felhasználva az elektromos térerősségre az

\begin{matrix} E_{A} \approx \frac{q}{4 π ε_{0} r^{2}} (1 - \frac{R}{d} + \frac{2 R}{r} (\frac{R^{2}}{d^{2}} - 1)) e_{A} \end{matrix}

közelítő formula adódik. Látható, hogy a fémgömb árnyékoló hatása mellett is nagy távolság esetén a távolság négyzetével csökken az elektromos térerősség.

c)

Mi a feltétele a teljes leárnyékolásnak?
A korábban levezetett képletekből látható, hogy a

d \to R

határesetben válna teljessé a leárnyékolás.

3. részfeladat.

a)

Mekkora és milyen irányú a kitérített ingára ható elektrosztatikus erő?

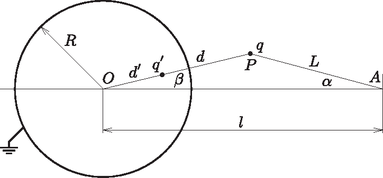3. ábra. Az

α

szöggel kitérített inga és a rá ható tükörtöltés

A fémgömb által kifejtett erő megegyezik a töltés és a tükörtöltés között fellépő Coulomb-erővel. Az

O A P

háromszögre felírt koszinusztétel alapján

\begin{matrix} d = \sqrt[]{l^{2} + L^{2} - 2 l L cos α} . \end{matrix}

Így a

q

töltésre ható erő nagysága:

\begin{matrix} F = \frac{1}{4 π ε_{0}} \frac{q q'}{{(d - d')}^{2}} = \frac{1}{4 π ε_{0}} \frac{q^{2} R d}{{(d^{2} - R^{2})}^{2}} = \frac{1}{4 π ε_{0}} \frac{q^{2} R \sqrt[]{l^{2} + L^{2} - 2 l L cos α}}{{(l^{2} + L^{2} - 2 l L cos α - R^{2})}^{2}} . \end{matrix}

Az erő a gömb középpontja felé mutat.

b)

Mekkora az erő fonalra merőleges komponense?
Az

O A P

háromszög

P

csúcsnál levő külső szöge

α + β

, így a keresett komponens

F_{⊥} = F sin (α + β)

. A szinusztétel alapján

sin (α + β) = \frac{l}{d} sin α

, így:

\begin{matrix} F_{⊥} = F \frac{l}{d} sin α = \frac{1}{4 π ε_{0}} \frac{q^{2} R l sin α}{{(l^{2} + L^{2} - 2 l L cos α - R^{2})}^{2}} . \end{matrix}

c)

Mennyi az inga kis rezgéseinek frekvenciája?
A matematikai inga mozgásegyenlete

m L \ddot{α} = - F_{⊥}

. Kicsiny kitérések esetén

sin α \approx α

cos α \approx 1

, így a mozgásegyenlet alakja ekkor:

\begin{matrix} m L \ddot{α} = - \frac{1}{4 π ε_{0}} \frac{q^{2} R l}{{({(l - L)}^{2} - R^{2})}^{2}} α, \end{matrix}

ahonnan a kis rezgések körfrekvenciája:

\begin{matrix} ω = \frac{q}{{(l - L)}^{2} - R^{2}} \sqrt[]{\frac{R l}{4 π ε_{0} m L}} . \end{matrix}

4. részfeladat.
A feladatnak talán ez a része a legérdekesebb, mert ügyes gondolatmenetekkel szinte számolás nélkül megoldható. Jelölje

E_{kölcs}

q

töltés és a polarizált gömb közti elektrosztatikus kölcsönhatási energiát, legyen

E_{gömb}

a gömbön polarizált töltéseloszlás elektrosztatikus energiája, és

E_{össz}

a teljes rendszer energiája. A feladat három alkérdésben e három energia meghatározását kéri. Világos, hogy

\begin{matrix} E_{össz} = E_{kölcs} + E_{gömb}, \end{matrix}

tehát bármely két energia ismeretében a harmadik könnyen meghatározható. Mi most egymástól függetlenül határozzuk meg a három energiát, és a végén ellenőrizzük, hogy teljesül rájuk a fenti feltétel.

a)

Mennyi a

q

töltés és a gömbön levő töltések közti

E_{kölcs}

elektrosztatikus kölcsönhatási energia?
Ez a kölcsönhatási energia negatív, hiszen a

q

töltés és a gömb vonzzák egymást. A kölcsönhatási energia abszolút értéke megegyezik azzal a munkával, melyet a gömb vonzása ellenében végeznünk kell, hogy a

q

töltést a végtelenbe távolítsuk, miközben a töltések a gömbön nem mozdulnak el. A gömbön polarizált töltés hatása a gömbön kívül pont olyan, mint a

q'

tükörtöltésé, tehát úgy is képzelhetjük, hogy

q

-t a rögzített

q'

tükörtöltéstől távolítjuk el. Így a kölcsönhatási energia megegyezik a

q

és

q'

közti elektrosztatikus energiával:

\begin{matrix} E_{kölcs} = \frac{1}{4 π ε_{0}} \frac{q q'}{d - d'} = - \frac{1}{4 π ε_{0}} \frac{q^{2} R}{d^{2} - R^{2}} . \end{matrix}

b)

Mennyi a gömbön levő töltéselrendeződés

E_{gömb}

elektrosztatikus energiája?
Gondolatban tekintsük a polarizált gömböt sok kis

q_{i}

töltésből álló rendszernek, melyek a gömbfelszín

r_{i}

pontjaiban vannak. A keresett energia a párkölcsönhatási energiák összege:

\begin{matrix} E_{gömb} = \sum_{i < j}^{} E_{i, j} = \frac{1}{2} \sum_{i}^{} \sum_{j \neq i}^{} E_{i, j}, \end{matrix}

ahol

\begin{matrix} E_{i, j} = \frac{1}{4 π ε_{0}} \frac{q_{i} q_{j}}{| r_{i} - r_{j} |} = q_{i} Φ_{j} (r_{i}) = q_{j} Φ_{i} (r_{j}) . \end{matrix}

(Itt

Φ_{i} (r)

q_{i}

töltés elektromos potenciálját jelöli az

r

helyen.) Ezt felhasználva:

\begin{matrix} E_{gömb} = \frac{1}{2} \sum_{i}^{} q_{i} \sum_{j}^{} Φ_{j} (r_{i}) . \end{matrix}

De a gömb felszínén, illetve azon kívül a polarizált töltésrendszer hatása helyettesíthető a tükörtöltés hatásával, tehát

\sum_{j} Φ_{j} (r_{i}) = Φ_{q'} (r_{i})

. Így

\begin{matrix} E_{gömb} = \frac{1}{2} \sum_{i}^{} q_{i} Φ_{q'} (r_{i}) = \frac{q'}{2} \sum_{i}^{} Φ_{i} (d') . \end{matrix}

A fémgömbben, a tükörtöltés

d'

helyén a zérus elektromos potenciált a gömbön polarizált töltések és a gömbön kívül a

d

pontban található

q

töltés potenciáljának szuperpozíciója alakítja ki, tehát

\sum_{i} Φ_{i} (d') = - Φ_{q} (d')

. Ezt felhasználva végül:

\begin{matrix} E_{gömb} = - \frac{q'}{2} Φ_{q} (d') = \frac{- 1}{2} E_{q, q'} = \frac{- 1}{2} E_{kölcs} = \frac{1}{8 π ε_{0}} \frac{q^{2} R}{d^{2} - R^{2}} . \end{matrix}

Látható, hogy az eredményhez az összegzéseket ténylegesen nem kellett elvégeznünk, csak ügyes okoskodásokra, a tükörtöltés módszer és a szuperpozíció elv pontos ismeretére volt szükségünk.

c)

Mennyi a rendszer teljes elektrosztatikus energiája?
A teljes kölcsönhatási energia negatív, abszolút értéke megegyezik azzal a munkával, ami a

q

töltésnek a földelt fémgömbtől végtelen meszire való eltávolításához szükséges, miközben a fémgömbön is szabadon vándorolhatnak a töltések. Az 1. részfeladat

c)

pontjában már meghatároztuk a gömb középpontjától

d

távolságra levő

q

töltésre ható

F (d)

erőt, tehát

\begin{matrix} E_{össz} & = - \int_{x = d}^{\infty} F (x) d x = - \frac{q^{2} R}{4 π ε_{0}} \int_{x = d}^{\infty} \frac{x}{{(x^{2} - R^{2})}^{2}} d x = \\ = \frac{q^{2} R}{8 π ε_{0}} {[\frac{1}{x^{2} - R^{2}}]}_{x = d}^{\infty} = - \frac{1}{8 π ε_{0}} \frac{q^{2} R}{d^{2} - R^{2}} . \end{matrix}

Látható, hogy teljesül az

E_{össz} = E_{kölcs} + E_{gömb}

egyenlőség, és az energiák aránya

\begin{matrix} E_{össz} : E_{kölcs} : E_{gömb} = (- 1) : (- 2) : (+ 1) . \end{matrix}

2. feladat. Kéményfizika

1. részfeladat.

a)

Mekkora minimális magasság mellett működik hatékonyan a kémény?
Jelölje

p (z)

a külső légnyomást

z

magasságban. Jó közelítéssel:

\begin{matrix} p (z) = p (0) - ϱ_{levegő} g z, \end{matrix}

(1)

ahol

p

(0) a talajszinti légnyomás. A kéményben áramló füstre alkalmazhatjuk a Bernoulli-törvényt:

\begin{matrix} \frac{1}{2} ϱ_{füst} v {(z)}^{2} + ϱ_{füst} g z + p_{füst} (z) = állandó, \end{matrix}

(2)

ahol

p_{füst} (z)

a füst nyomása

z

magasságban,

ϱ_{füst}

a füst sűrűsége, és

v (z)

jelöli a füst sebességét. (Felhasználtuk azt a közelítést, hogy a füst sűrűsége nem változik a kéményben.)
A Bernoulli-törvény segítségével két pontot hasonlítunk össze; a talajszinten lévő kazánt (ahol a füst jó közelítéssel még nem mozog) és a kémény tetőpontját. A kémény akkor működik, ha a felső nyílásában a nyomás nagyobb (vagy egyenlő), mint a külső légnyomás (1). Minimális kéménymagasságnál az egyenlőség teljesül:

\begin{matrix} \frac{1}{2} ϱ_{füst} v {(h)}^{2} + ϱ_{füst} g h + p_{füst} (h) = & (3) \\ = & \frac{1}{2} ϱ_{füst} v {(h)}^{2} + ϱ_{füst} g h + p (0) - ϱ_{levegő} g h \approx p (0), \end{matrix}

amiből kiszámíthatjuk a füst sebességét:

\begin{matrix} v (h) = \sqrt[]{2 g h (\frac{ϱ_{levegő}}{ϱ_{füst}} - 1)} . \end{matrix}

(4)

A kémény akkor működik hatékonyan, ha a kazánból származó összes égéstermék kijut a légkörbe a kémény tetején, vagyis

\begin{matrix} v (h) \geq \frac{B}{A} . \end{matrix}

(5)

A (4) és (5) egyenletek összevetésével a kémény magasságára a következő feltételt kapjuk:

\begin{matrix} h \geq \frac{B^{2}}{A^{2}} \frac{1}{2 g} \frac{1}{\frac{ϱ_{levegő}}{ϱ_{füst}} - 1} . \end{matrix}

(6)

A kazánban a füstöt ideális gázként kezeljük, melynek nyomása a talajszinti

p (0)

légnyomás. Így a levegő és a füst sűrűsége között a következő összefüggés írható fel:

\begin{matrix} \frac{ϱ_{levegő}}{ϱ_{füst}} = \frac{T_{füst}}{T_{levegő}}, \end{matrix}

(7)

melynek segítségével megkaphatjuk a kémény minimális magasságát:

\begin{matrix} h \geq \frac{B^{2}}{A^{2}} \frac{1}{2 g} \frac{T_{levegő}}{T_{füst} - T_{levegő}} = \frac{B^{2}}{A^{2}} \frac{1}{2 g} \frac{T_{levegő}}{Δ T} = h_{{min}_{}^{}} . \end{matrix}

(8)

b)

Milyen magas a meleg vidéken épült kémény?
A (8) összefüggés alapján:

\begin{matrix} \frac{h_{meleg}}{h_{hideg}} = \frac{\frac{T_{meleg}}{T_{füst} - T_{meleg}}}{\frac{T_{hideg}}{T_{füst} - T_{hideg}}} \Rightarrow h_{meleg} = 145 m. \end{matrix}

(9)

c)

Hogyan változik a gázok sebessége a kéményben?
A (4) és a (7) összefüggések alapján láthatjuk, hogy a kéményben a füst sebessége:

\begin{matrix} v (h) = \sqrt[]{2 g h (\frac{ϱ_{levegő}}{ϱ_{füst}} - 1)} = \sqrt[]{2 g h (\frac{T_{füst}}{T_{levegő}} - 1)} = \sqrt[]{2 g h (\frac{Δ T}{T_{levegő}})} . \end{matrix}

(10)

Mivel abban a közelítésben dolgozunk, ahol a füst sűrűsége állandó, a kontinuitási egyenlet (

A v = állandó

) következménye az, hogy az állandó keresztmetszetű kéményben állandó a füst áramlási sebessége. Minimális kéménymagasság esetén ez az állandó sebesség:

v = B / A

. Vegyük észre, hogy a kazánban a füst még gyakorlatilag áll, majd a kéménybe történő belépéskor egy rövid szakaszon a füstgázok állandó értékre gyorsulnak fel.

d)

Hogyan változik a kéményben a gáz nyomása a magasság függvényében?
A Bernoulli-egyenletet alkalmazzuk a kémény tetejére és egy tetszőleges,

z

magasságú pontra. Kihasználjuk, hogy a füstsebesség állandó:

\begin{matrix} p (h) + \frac{1}{2} ϱ_{füst} v^{2} + ϱ_{füst} g h = p (z) + \frac{1}{2} ϱ_{füst} v^{2} + ϱ_{füst} g z . \end{matrix}

(11)

Használjuk fel az (1) egyenletet

p (h)

kifejezésére:

p (h) = p (0) - ϱ_{levegő} g h

, és fejezzük ki a kérdéses nyomást:

\begin{matrix} p (z) = p (0) - (ϱ_{levegő} - ϱ_{füst}) g h - ϱ_{füst} g z . \end{matrix}

(12)

Láthatjuk, hogy a talajszinten (

z = 0

) a kéményben a nyomás kisebb a külső légnyomásnál, vagyis amikor a füst a kazánból a kéménybe jut, akkor nemcsak a sebessége változik (növekszik), a nyomása is ugrásszerűen lecsökken.

2. részfeladat.

a)

Mennyi a napkémény hatásfoka?
A kémény által

Δ t

idő alatt kibocsátott forró levegő mozgási energiája így írható fel a (10) összefüggés segítségével:

\begin{matrix} E_{mozg} = \frac{1}{2} (A v Δ t ϱ_{forró}) v^{2} = (A v Δ t ϱ_{forró}) g h \frac{Δ T}{T_{levegő}} . \end{matrix}

(13)

Jelöljük a kémény léghozamát

w

-vel, ami megmutatja a kéményen másodpercenként áthaladó levegő tömegét (

w = \frac{Δ m}{Δ t} = A v ϱ_{forró}

). A kémény teljesítménye így fejezhető ki

w

-vel:

\begin{matrix} P_{hasznos} = w g h \frac{Δ T}{T_{levegő}} . \end{matrix}

(14)

A napsugárzás által leadott teljesítmény a

G

napállandótól és az

S

felülettől függ:

\begin{matrix} P_{sugárzás} = G S = w c Δ T, \end{matrix}

(15)

ahol

c

a levegő fajhője. Így a napkémény maximális elméleti hatásfoka:

\begin{matrix} η = \frac{P_{hasznos}}{P_{sugárzás}} = \frac{g h}{c T_{levegő}} . \end{matrix}

(16)

b)

Hogyan függ a hatásfok a magasságtól?
A magasságfüggés lineáris.

3. részfeladat.

a)

Mekkora a Manzanares-ben épült napkémény hatásfoka?
A hatásfok:

\begin{matrix} η = \frac{g h}{c T_{levegő}} = 0, 0064 = 0, 64 % . \end{matrix}

(17)

b)

Mekkora teljesítménnyel működik a napkémény Manzanares-ben?
A napkémény teljesítménye:

\begin{matrix} P = G S η = G (r^{2} π) η = 45 kW. \end{matrix}

(18)

c)

Mennyi energiát állít elő egy napsütéses napon a manzanares-i napkémény?
Ha napi nyolc óra napsütést tételezünk fel, akkor az előállított energia 360 kWh.

4. részfeladat.

a)

Mekkora a napkéménybe lépő levegő hőmérséklet ugrása?
Fejezzük ki a

w

léghozamot a (10) és a (15) összefüggésekkel:

\begin{matrix} w & = A v ϱ_{forró} = A \sqrt[]{2 g h \frac{Δ T}{T_{levegő}}} ϱ_{forró}, & (19) \\ w & = \frac{G S}{c Δ T}, \end{matrix}

amiből kifejezhetjük a

Δ T

hőmérsékletugrást:

\begin{matrix} Δ T = {(\frac{G^{2} S^{2} T_{levegő}}{A^{2} c^{2} ϱ_{forró}^{2} 2 g h})}^{1 / 3} \approx 9, 1 K. \end{matrix}

(20)

b)

Mekkora a napkémény léghozama Manzanares-ben?
A (19) ikerösszefüggés alapján:

\begin{matrix} w = 760 kg/s. \end{matrix}

(21)

3. feladat. Egyszerű atommagmodell

1. részfeladat.

a)

Egyszerű kockarácsot feltételezve, mennyi a nukleonok kitöltési tényezője?
A kocka oldaléle (a rácsállandó) legyen

a

. Az egymással érintkező nukleongömbök sugara így

r = \frac{a}{2}

. Egy kockára éppen nyolc nyolcad-gömb jut, tehát az

f

kitöltési tényező egyszerűen egy gömb és a kocka térfogatának aránya:

\begin{matrix} f = \frac{V_{gömb}}{V_{kocka}} = \frac{\frac{4}{3} r^{3} π}{a^{3}} = \frac{\frac{4}{3} {(\frac{a}{2})}^{3} π}{a^{3}} = \frac{π}{6} \approx 0, 52. \end{matrix}

(1)

b)

Mekkora az

A

tömegszámú atommag tömegsűrűsége, töltéssűrűsége és sugara?
Az atommag tömegsűrűsége:

\begin{matrix} ϱ_{m} = f \frac{m_{N}}{V_{N}} = f \frac{m_{N}}{\frac{4}{3} r_{N}^{3} π} = 0, 52 \cdot \frac{1, 67 \cdot 10^{- 27}}{\frac{4}{3} {(0, 85 \cdot 10^{- 15})}^{3} π} \approx 3, 40 \cdot 10^{17} {kg/m}^{3} . \end{matrix}

(2)

Az atommag töltéssűrűsége:

\begin{matrix} ϱ_{c} = \frac{f}{2} \frac{e}{V_{N}} = \frac{f}{2} \frac{e}{\frac{4}{3} r_{N}^{3} π} = \frac{0, 52}{2} \cdot \frac{1, 6 \cdot 10^{- 19}}{\frac{4}{3} {(0, 85 \cdot 10^{- 15})}^{3} π} \approx 1, 63 \cdot 10^{25} {C/m}^{3}, \end{matrix}

(3)

ahol figyelembe vettük, hogy csak a protonoknak van töltésük, ugyanannyi neutronnak nincs.
Ha a nukleonok száma

A

, akkor az atommag térfogata így fejezhető ki:

\begin{matrix} V = \frac{A V_{N}}{f} . \end{matrix}

(4)

Ennek megfelelően az atommag sugara:

\begin{matrix} R = r_{N} {(\frac{A}{f})}^{1 / 3} = \frac{0, 85}{0, 52^{1 / 3}} A^{1 / 3} \approx 1, 06 fm\cdotA^{1 / 3}, \end{matrix}

(5)

ahol az 1,06 fm-es szorzótényezőt a továbbiakban

r_{0}

-lal jelöljük.

2. részfeladat.
Mekkora az

A

tömegszámú atommag kötési energiája?
A felületi nukleonokat egy 2

r_{N}

vastagságú héjban képzeljük el az atommag felszínén. Így kiszámíthatjuk a felületi nukleonok számát:

\begin{matrix} A_{felület} = f \frac{V_{felület}}{V_{N}}, \end{matrix}

(6)

ahol a felszíni gömbhéj térfogata:

\begin{matrix} V_{felület} = \frac{4}{3} R^{3} π - \frac{4}{3} {(R - 2 r_{N})}^{3} π . \end{matrix}

(7)

A kötési energiához a felületi nukleonok feleakkora taggal járulnak hozzá, mint az atommag belsejében lévők:

\begin{matrix} E_{b} = (A - A_{felület}) a_{V} + A_{felület} \frac{a_{V}}{2} . \end{matrix}

(8)

Az (5), (6) és (7) összefüggések figyelembevételével a (8) kötési energiára ezt az eredményt kapjuk:

\begin{matrix} E_{b} & = A a_{V} - A_{felület} \frac{a_{V}}{2} = A a_{V} - 3 f^{1 / 3} A^{2 / 3} a_{V} + 6 f^{2 / 3} A^{1 / 3} a_{V} - 4 f a_{V} = & (9) \\ = (15, 8 A - 38, 2 A^{2 / 3} + 61, 6 A^{1 / 3} - 33, 1) MeV. \end{matrix}

3. részfeladat.

a)

Mekkora az atommag elektrosztatikus energiája?
Ha a megadott képletben

Q_{0}

helyére

Z e

értéket helyettesítünk, akkor az atommag elektrosztatikus energiájára ezt az összefüggést kapjuk:

\begin{matrix} U_{C} = \frac{3 {(Z e)}^{2}}{20 π ε_{0} R} = \frac{3 Z^{2} e^{2}}{20 π ε_{0} R} . \end{matrix}

(10)

Vegyük figyelembe, hogy a protonok önmagukra nem hatnak, tehát (az útmutatás szerint)

Z^{2}

helyére

Z (Z - 1)

-et kell írnunk:

\begin{matrix} U_{C} = \frac{3 Z (Z - 1) e^{2}}{20 π ε_{0} R} . \end{matrix}

(11)

b)

Hogyan írható fel az atommag teljes kötési energiája?
A teljes kötési energia úgy írható fel, hogy a (9) kifejezésből kivonjuk a (11) Coulomb-tagot, mert a pozitív elektrosztatikus energia csökkenti az atommag kötési energiáját. (A kötési energiát úgy értelmezzük, mint az atommag nukleonokra bontásához szükséges minimális energiát.) A számolás során az atommag

R

sugarára az (5) összefüggést használjuk, továbbá kihasználjuk azt is, hogy

Z \approx \frac{A}{2}

\begin{matrix} E_{b}^{teljes} = E_{b} - U_{C} = & (12) \\ = A a_{V} - 3 f^{1 / 3} A^{2 / 3} a_{V} + 6 f^{2 / 3} A^{1 / 3} a_{V} - 4 f a_{V} - \frac{3 Z (Z - 1) e^{2}}{20 π ε_{0} R} = \\ = A a_{V} - 3 f^{1 / 3} A^{2 / 3} a_{V} + 6 f^{2 / 3} A^{1 / 3} a_{V} - 4 f a_{V} - \frac{3 e^{2} f^{1 / 3}}{20 π ε_{0} r_{N}} (\frac{A^{5 / 3}}{4} - \frac{A^{2 / 3}}{2}) . \end{matrix}

4. részfeladat.

a)

Mekkora a bomlástermékek együttes mozgási energiája?
A bomlástermékek együttes mozgási energiáját a kötési energiák különbségéből, illetve a két fél mag

(\frac{Z}{2} = \frac{A}{4})

Coulomb-energiájának figyelembevételéből határozhatjuk meg:

\begin{matrix} E_{mozg} (d) = & 2 E_{b}^{teljes} (\frac{A}{2}) - E_{b}^{teljes} (A) - \frac{1}{4 π ε_{0}} \frac{A^{2} e^{2}}{4^{2} d} = & (13) \\ = & - 3 f^{1 / 3} A^{2 / 3} a_{V} (2^{1 / 3} - 1) + 6 f^{2 / 3} A^{1 / 3} a_{V} (2^{2 / 3} - 1) - 4 f a_{V} - \\ - \frac{3 e^{2} f^{1 / 3}}{20 π ε_{0} r_{N}} [\frac{A^{5 / 3}}{4} (2^{- 2 / 3} - 1) - \frac{A^{2 / 3}}{2} (2^{1 / 3} - 1)] - \frac{1}{4 π ε_{0}} \frac{A^{2} e^{2}}{16 d} . \end{matrix}

Vegyük észre, hogy az

A a_{V}

típusú fő járulékok kiestek.

b)

Mekkora tömegszám esetén lehetséges bomlás?
A mozgási energia fenti (13) kifejezésébe helyettesítsük be a

d = 2 R (\frac{A}{2})

távolságot:

\begin{matrix} E_{mozg} = & 2 E_{b}^{teljes} (\frac{A}{2}) - E_{b}^{teljes} (A) - \frac{1}{4 π ε_{0}} \frac{2^{1 / 3} A^{2} e^{2}}{16 \cdot 2 r_{N} A^{1 / 3} f^{- 1 / 3}} = & (14) \\ = & - 3 f^{1 / 3} A^{2 / 3} a_{V} (2^{1 / 3} - 1) + 6 f^{2 / 3} A^{1 / 3} a_{V} (2^{2 / 3} - 1) - 4 f a_{V} - \\ - \frac{e^{2} f^{1 / 3}}{π ε_{0} r_{N}} [\frac{3}{80} (2^{- 2 / 3} - 1) + \frac{2^{1 / 3}}{128}] A^{5 / 3} - \frac{e^{2} f^{1 / 3}}{π ε_{0} r_{N}} [\frac{3}{40} (2^{1 / 3} - 1)] A^{2 / 3} = \\ = & (0, 02203 A^{5 / 3} - 10, 0365 A^{2 / 3} + 36, 175 A^{1 / 3} - 33, 091) MeV. \end{matrix}

A megadott tömegszámokat numerikusan behelyettesítve a következő értékeket kapjuk:

\begin{matrix} A & = 100 & \to & E_{mozg} & = - 33, 95 MeV,  A  = 150\toE_{mozg}=-30,93 MeV,A  = 200\toE_{mozg}=-14,10 MeV,A  = 250\toE_{mozg}= +15,06 MeV. \end{matrix}

Modellünk szerint a bomlás akkor következik be, ha a mozgási energia értéke pozitív. Durva becsléssel ez nagyjából

A > 225

esetén teljesül. (Pontosabb számítással a mozgási energia

A = 227

-nél vált előjelet.)

5. részfeladat.

a)

Mekkora a nikkelmag gerjesztési energiája a transzfer reakció után?
Ezt a részkérdést nemrelativisztikusan és relativisztikusan is meg lehet oldani. Az Olvasóra bízzuk, hogy melyik módszert tartja egyszerűbbnek.
Nemrelativisztikus megoldás: Először is határozzuk meg, hogy mennyi tömeg alakul át energiává a reakcióban, vagyis határozzuk meg a reakció úgynevezett

Q

értékét. A tömegváltozás:

\begin{matrix} Δ m & = {(tömeg)}_{reakció után} - {(tömeg)}_{reakció előtt} = & (15) \\ = (57, 935 35 + 12, 000 00) u - (53, 939 62 + 15, 994 91) u = \\ = 0, 000 82 u = 1, 36 \cdot 10^{- 30} kg. \end{matrix}

(A fenti képletben u az atomi tömegegységet jelöli, amit régebben a.t.e., vagy az angol megfelelőjére utalva a.m.u. módon is írtak.) A tömeg növekedése azt mutatja, hogy a reakció után a termékek mozgási energiája kisebb kell legyen a kezdetinél. A reakció

Q

értéke:

\begin{matrix} Q & = {(mozgási energia)}_{reakció után} - {(mozgási energia)}_{reakció előtt} = & (16) \\ = - Δ m c^{2} = - 1, 224 \cdot 10^{- 13} J = - 0, 764 MeV. \end{matrix}

Használnunk kell (egy dimenzióban) a lendületmegmaradás, és az energiamegmaradás törvényét:

\begin{matrix} m (^{16} O) v (^{16} O) & = m (^{12} C) v (^{12} C) + m (^{58} Ni) v (^{58} Ni), & (17) \\ E_{mozg} (^{16} O) + Q & = E_{mozg} (^{12} C) + E_{mozg} (^{58} Ni) + E_{exc} (^{58} Ni), & (18) \end{matrix}

ahol az utolsó tag a nikkelmag gerjesztési energiája. Mivel a berepülő oxigénmag és a kirepülő szénatommag sebessége megegyezik, a lendületmegmaradási egyenlet így egyszerűsödik:

\begin{matrix} [m (^{16} O) - m (^{12} C)] v (^{16} O) = m (^{58} Ni) v (^{58} Ni) . \end{matrix}

(19)

A szén- és a nikkelmag mozgási energiáját kifejezhetjük a berepülő oxigén megadott mozgási energiája és az ismert magtömegek alapján, és ezt (egyszerű, bár kissé hosszadalmas számolás után) beírhatjuk az energia egyenletbe:

\begin{matrix} E_{exc} (^{58} Ni) = Q + E_{mozg} (^{16} O) - E_{mozg} (^{12} C) - E_{mozg} (^{58} Ni) = & (20) \\ = Q + E_{mozg} (^{16} O) \frac{[m (^{16} O) - m (^{12} C)] \cdot [m (^{58} Ni) + m (^{12} C) - m (^{16} O)]}{m (^{58} Ni) m (^{16} O)} \approx \\ \approx 10, 9 MeV. \end{matrix}

Érdekes észrevenni, hogy a végeredmény tört kifejezésének számlálójában lévő első szögletes zárójelben lényegében az átadott tömeg (egy alfa-részecske) szerepel, míg a második szögletes zárójelben a vasatommag tömege található.
Relativisztikus megoldás: Relativisztikusan így írhatjuk fel az energia- és az impulzusmegmaradást:

\begin{matrix} m (^{54} Fe) c^{2} + \frac{m (^{16} O) c^{2}}{\sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} & = \frac{m (^{12} C) c^{2}}{\sqrt[]{1 - \frac{v^{2} (^{12} C)}{c^{2}}}} + \frac{m^{*} (^{58} Ni) c^{2}}{\sqrt[]{1 - \frac{v^{2} (^{58} Ni)}{c^{2}}}}, & (21) \\ \frac{m (^{16} O) v (^{16} O)}{\sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} & = \frac{m (^{12} C) v (^{12} C)}{\sqrt[]{1 - \frac{v^{2} (^{12} C)}{c^{2}}}} + \frac{m^{*} (^{58} Ni) v (^{58} Ni)}{\sqrt[]{1 - \frac{v^{2} (^{58} Ni)}{c^{2}}}} . \end{matrix}

A fenti egyenletekben mindenhol a nyugalmi tömegek szerepelnek. A magasan gerjesztett nikkelmag nyugalmi tömege (

m^{*}

) nagyobb, mint az alapállapotú nikkelé, ezt jelzi a csillag.
Ha figyelembe vesszük, hogy az oxigén- és a szénmag sebessége megegyezik, akkor az egyenletek egyszerűsödnek:

\begin{matrix} m (^{54} Fe) + \frac{m (^{16} O) - m (^{12} C)}{\sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} & = \frac{m^{*} (^{58} Ni)}{\sqrt[]{1 - \frac{v^{2} (^{58} Ni)}{c^{2}}}}, & (22) \\ \frac{[m (^{16} O) - m (^{12} C)] v (^{16} O)}{\sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} & = \frac{m^{*} (^{58} Ni) v (^{58} Ni)}{\sqrt[]{1 - \frac{v^{2} (^{58} Ni)}{c^{2}}}} . \end{matrix}

Ha az utóbbi két egyenletet elosztjuk egymással, akkor a nikkelmag sebességét ki tudjuk fejezni az oxigén sebességével és tömegadatokkal:

\begin{matrix} v (^{58} Ni) = \frac{[m (^{16} O) - m (^{12} C)] \cdot v (^{16} O)}{[m (^{16} O) - m (^{12} C)] + m (^{54} Fe) \sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} . \end{matrix}

(23)

Az oxigén sebességét pedig a mozgási energia relativisztikus alakjából fejezhetjük ki:

\begin{matrix} E_{mozg} (^{16} O) = \frac{m (^{16} O) c^{2}}{\sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} - m (^{16} O) c^{2}, \end{matrix}

(24)

amiből kissé fáradságos átrendezés után

\begin{matrix} v (^{16} O) = \sqrt[]{1 - {(\frac{m (^{16} O) c^{2}}{E_{mozg} (^{16} O) + m (^{16} O) c^{2}})}^{2}} \cdot c \approx 0, 081 72 \cdot c \approx 2, 45 \cdot 10^{7} \frac{m}{s} . & (25) \end{matrix}

Ezt az értéket (23)-ba helyettesítve megkapjuk a nikkelmag sebességét:

\begin{matrix} v (^{58} Ni) = \frac{[m (^{16} O) - m (^{12} C)] \cdot v (^{16} O)}{[m (^{16} O) - m (^{12} C)] + m (^{54} Fe) \sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} \approx 1, 69 \cdot 10^{6} \frac{m}{s} . \end{matrix}

(26)

Mindezek után kiszámíthatjuk a gerjesztett állapotú nikkelmag tömegét:

\begin{matrix} m^{*} (^{58} Ni) = [m (^{16} O) - m (^{12} C)] \cdot \frac{\sqrt[]{1 - \frac{v^{2} (^{58} Ni)}{c^{2}}}}{\sqrt[]{1 - \frac{v^{2} (^{16} O)}{c^{2}}}} \cdot \frac{v (^{16} O)}{v (^{58} Ni)} \approx 57, 95 u. \end{matrix}

(27)

Ezek után a nikkelmag gerjesztési energiájának kiszámítása már gyerekjáték:

\begin{matrix} E_{exc} = [m^{*} (^{58} Ni) - m (^{58} Ni)] c^{2} = 10, 8636 MeV. \end{matrix}

Három értékes jegyre pontosan visszakaptuk a nemrelativisztikusan számolt végeredményt, ami azt mutatja, hogy jogos volt a nemrelativisztikus számolás.

b)

Mekkora a nikkelmag által kibocsátott gamma-foton energiája a kétféle vonatkoztatási rendszerben?
Újra az energia- és az impulzusmegmaradás törvényét kell felírnunk a nikkelmagra. Az egyenletek bal oldalára a gerjesztett állapotot jellemző tagokat írjuk, míg a jobb oldalukra a ,,legerjesztés'' utáni tagokat:

\begin{matrix} E_{exc} (^{58} Ni) & = E_{γ} + E_{visszalökődés}, & (28) \\ 0 & = p_{γ} - p_{visszalökődés}, \end{matrix}

ahol az impulzusokat az atom- és magfizikában megszokott módon

p

-vel jelöltük. A fotonok energiája és impulzusa között a következő általános összefüggés érvényes:

\begin{matrix} E_{γ} = p_{γ} c . \end{matrix}

(29)

A nikkelmag visszalökődési energiáját klasszikusan számolhatjuk, hiszen az előzőekben láttuk, hogy a problémát jól kezelhetjük nemrelativisztikusan is:

\begin{matrix} E_{visszalökődés} = \frac{p_{visszalökődés}^{2}}{2 m (^{58} Ni)} = \frac{p_{γ}^{2}}{2 m (^{58} Ni)} = \frac{E_{γ}^{2}}{2 m (^{58} Ni) \cdot c^{2}} . \end{matrix}

(30)

Eredményünket helyettesítsük be a (28) energiamegmaradási egyenletébe:

\begin{matrix} E_{exc} (^{58} Ni) = E_{γ} + E_{visszalökődés} = E_{γ} + \frac{E_{γ}^{2}}{2 m (^{58} Ni) \cdot c^{2}}, \end{matrix}

(31)

ami

E_{γ}

-ra nézve egy másodfokú egyenlet. Ennek fizikailag értelmes megoldása:

E_{γ} = 10, 8625

MeV, vagyis ennyi a gamma-foton energiája abban a vonatkozási rendszerben, amelyben a gerjesztett nikkelmag nyugalomban van. Mindezek után már könnyen meghatározhatjuk a nikkelmag visszalökődési energiáját:

\begin{matrix} E_{visszalökődés} = E_{exc} (^{58} Ni) - E_{γ} = 1, 1 keV. \end{matrix}

(32)

Mivel a gammát sugárzó nikkelmag nagy sebességgel mozog a laboratóriumi rendszerben a detektor felé, így az észleléskor a detektor a relativisztikus Doppler-effektus szerint megváltozott frekvenciájúnak ,,érzi'' a vele szembe mozgó gamma-fotont:

\begin{matrix} f_{detektor} = f_{γ, kisugárzott} \sqrt[]{\frac{1 + β}{1 - β}} . \end{matrix}

(33)

A foton energiája és frekvenciája között érvényes a Planck-formula (

E = h f

), vagyis a fotonenergiákra is érvényes a Doppler-képlet:

\begin{matrix} E_{detektor} = E_{γ, kisugárzott} \sqrt[]{\frac{1 + β}{1 - β}}, \end{matrix}

(34)

ahol

β = \frac{v}{c}

. A nikkelmag sebességét a (26) összefüggés alapján számítottuk ki, aminek a felhasználásával megkapjuk a detektor által észlelt gamma-foton energiáját:

E_{detektor} = 10, 924

MeV.

Kísérleti feladat

A kísérleti feladat két részből állt, melyek megoldásához részben ugyanazokat a kísérleti eszközöket kellett használni.

1. feladat. Lapok rugalmassága
Ebben a feladatban írásvetítő fólia rugalmassági adatait, hajlítási szilárdságát és Young-moduluszát vizsgálták a versenyzők. Először a fóliát henger alakúra kellett hajlítani, majd egy speciális ,,préssel'' a hengert oldalról összenyomva a nyomóerő függvényében a benyomódást mérték. Az elrendezés elvi vázlata és fényképe az 1. ábrán látható.

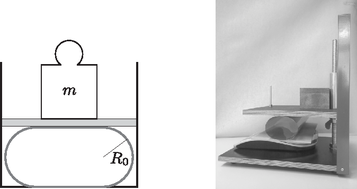1. ábra. Az elrendezés elvi rajza, és a henger alakúra hajlított fólia a rugalmasságát mérő présben

A prés alján egy digitális mérleg helyezkedett el, erről lehetett leolvasni az

F = m g

nyomóerőt. (A mérleg az

m

tömeget jelezte ki grammokban.) A prés felső lapját szárnyas anyacsavarral lehetett finoman mozgatni. A csavar elfordulásából következtetni lehetett a benyomódásra.
Elméleti megfontolások alapján a benyomott fólia alakja elegendően nagy összenyomás esetén jól közelíthető stadion alakkal, mely két

R_{0}

sugarú félkörből és két egyenes szakaszból áll. Ilyenkor az

R_{0}

sugár és az

F

nyomóerő között az

\begin{matrix} R_{0}^{2} = \frac{l κ π}{2 F} \end{matrix}

(

*

)

összefüggés áll fenn, ahol

κ

a fólia anyagára jellemző hajlítási szilárdság,

l

pedig a henger magassága. Látható, hogy az elrendezés nem ideális rugóként viselkedik.
A versenyzőknek össze kellett állítaniuk a kísérleti elrendezést, és több fólia esetén is meg mérték az

F

erőt a prés

2 R_{0}

szélességének függvényében. Fel kellett ismerjenek bizonyos szimmetriákat, továbbá feladatuk volt az egyensúlyi helyzetek megkeresése és ezek stabilitás-vizsgálata. Ezután alkalmasan transzformált adatok ábrázolásával igazolni kellett, hogy a

(*)

formula valóban helyes egy bizonyos

R_{0} < R_{c}

tartományban. Végül meg kellett határozni az

\frac{R_{0}}{R_{c}}

értéket, a

κ

hajlítási szilárdságot, és abból adott összefüggés alapján a fólia Young-moduluszát.
Kiértékeléskor nagyon fontos, hogy olyan transzformált mennyiségeket ábrázoljunk a grafikonon, melyek között lineáris kapcsolat van. Például ábrázolhatjuk

R_{0}^{2}

-et a mérleg által mutatott

m = F / g

tömeg reciprokának függvényében. A 2. ábrán egy valódi mérésből származó grafikon látható. A nyíl jelzi a stadion közelítés érvényességi tartományát. Jól láthatóan ebben a tartományban a transzformált adatok között egyenes arányosság áll fenn.

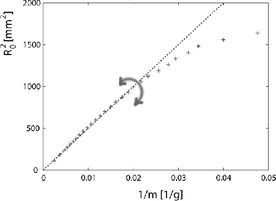2. ábra. Az

x = 1 / m = g / F

y = R_{0}^{2}

mennyiségek ábrázolásával kapott grafikon

2. feladat. Mágnesek közötti erők, stabilitásvizsgálat, szimmetriák
Ebben a feladatban a versenyzők egy hosszú rúdmágnes és egy gyűrű alakú mágnes közti erőt mérték a mágnesek közti távolság függvényében. Fel kellett ismerjenek bizonyos szimmetriákat, továbbá feladatuk volt az egyensúlyi helyzetek megkeresése és ezek stabilitásának vizsgálata. A gyűrű alakú mágnes egy átlátszó műanyagcső végére volt ragasztva. A rúdmágnest ebbe a csőbe kellett bedugni, ez biztosította, hogy a két mágnes tengelye mindig egy egyenesbe essék (3. ábra). Az erőt az előző mérésnél is használt digitális mérlegre szerelt préssel mérték.

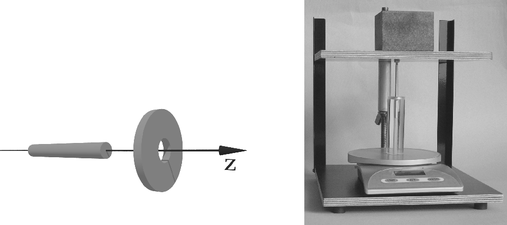3. ábra. A két mágnes elvi rajza, és elhelyezkedésük a présben

A megoldást nehezítette, hogy a rúdmágnesre csak a felfelé irányban ható erőt lehetett mérni, hiszen a prés csak tolni tud, húzni nem. Persze ha a rúdmágnes polaritását megfordítjuk, akkor az erő iránya is ellenkezőjére vált, így lehet felvennia teljes görbét. A 4. ábrán látható a mágnesek között mért

F

erő a rúdmágnes

z

helyzetének függvényében párhuzamos, illetve ellentétes polaritás esetén. (A két mágnes középpontjának távolsága

z

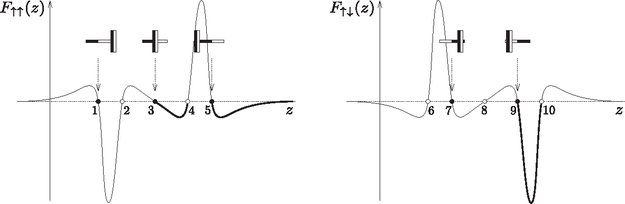4. ábra. A két mágnes között mérhető

F

erő a

z

távolság függvényében párhuzamos, illetve ellentétes polaritás esetén

A görbék meglepően bonyolultak, annak ellenére, hogy több érdekes szimmetriát is mutatnak! Mindkét függvény páratlan függvény, és az egyik mágnes polaritásának megváltoztatásakor az erő is előjelet vált, azaz:

\begin{matrix} F_{↑ ↑} (z) = - F_{↑ ↑} (- z), F_{↑ ↓} (z) = - F_{↑ ↓} (- z), F_{↑ ↑} (z) = - F_{↑ ↓} (z) . \end{matrix}

A görbék zérushelyei felelnek meg az egyensúlyi helyzeteknek. Az egyensúly stabil, ha az erő az egyensúlyból való kitérítéssel ellentétes irányú, azaz ha a görbe negatív meredekséggel metszi az

x

tengelyt. Ellenkező esetben az egyensúlyi helyzet instabil. Az ábrán teli körök jelölik a stabil, üres körök az instabil egyensúlyi helyzeteket.
A versenyzőknek az egyensúlyi helyzeteket kellett megkeresniük és osztályozniuk, a szimmetriákat kellett megállapítaniuk, és az

F (z)

grafikonok egyes szakaszait kimérve, a szimmetriák figyelembevételével kvalitatíven fel kellett rajzolniuk a teljes grafikonok menetét.

\begin{matrix} Honyek GyulaésTasnádi Tamás \end{matrix}

¹ Az elméleti feladatok szövegét a múlt havi számunkban közöltük.