Cím: Tudományos népszerűsítő előadások a Fővárosi Fazekas Mihály Gimnáziumban
Szerző(k):  Hraskó András 
Füzet: 2010/szeptember, 353 - 354. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tudományos népszerűsítő előadások
a Fővárosi Fazekas Mihály Gimnáziumban
 

Hraskó András
 

2010. október 5-én kedden 16 órától Virág Bálint, iskolánk volt diákja, a kanadai Toronto Egyetem munkatársa mesél véletlen gráfokról a Fővárosi Fazekas Mihály Gimnáziumban. Friss információk a http://matek.fazekas.hu/portal/eloadas/ linken olvashatók. Az iskola címe: 1082 Budapest, Horváth Mihály tér 8.
 
Alább az előadó által írt beharangozó olvasható.
 
Véletlen gráfok
 

Két párhuzamos út (e 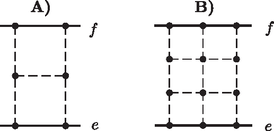és f) között
 
A) 1×2-es,  B) 2×3-as
 
négyzetrács elrendezésben terveznek utakat. Ha a rácspontok közötti mindegyik kis útszakasz (az egyik esetben 5, a másikban 13 ilyen van) egymástól függetlenül 12 valószínűséggel épül meg illetve nem épül meg, akkor mennyi az esélye, hogy az e, f utak egyikéről át lehet jutni a másikra a megépülő utakon át?
 

 
1. ábra
 

Általában, ha egy gráfból úgy készítünk új gráfot, hogy éleit egymástól függetlenül p valószínűséggel megtartjuk, 1-p valószínűséggel pedig elhagyjuk, akkor perkolációról beszélünk. A perkolációk vizsgálatának nagy lökést adott a felismerés, hogy általuk nagy hálózatok is modellezhetők, elemezhetők.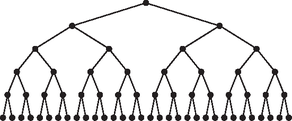
 

 
2. ábra
 

Az egyik tipikus kérdés, hogy a létrejövő ,,nagy'' hálózatban vagyis gráfban van-e ,,nagy'' összefüggő részgráf, tehát csúcspontok egymással élekkel összekötésben álló rendszere. A ,,nagy''-ot a matematika a ,,végtelen''-nel nevezi meg, így például már bizonyított az alábbi két eredmény:
 
I. tétel: Ha a kiinduló gráf a 2. ábrán látható, de végtelenül folytatódó 3-reguláris fa és p<12, akkor nulla annak a valószínűsége, hogy a perkolációban van végtelen összefüggő részgráf.
 

II. tétel: A (mindegyik irányban) végtelen négyzetrács perkolációjában pontosan akkor lesz végtelen összefüggő részgráf, hogy ha p>12.
 

A téma nehézségét mutatja, hogy a II. tétel három dimenziós változata máig megoldatlan.