Cím:	A 2009-2010. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2010/november, 450 - 455. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A 2009‐2010. évi Arany Dániel Matematikai Tanulóverseny feladatai   KEZDŐK   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Hány (pozitív) osztója van a    $\begin{array}{c}{\displaystyle {\left(-1\right)}^0\cdot 1+{\left(-1\right)}^1\cdot 2+{\left(-1\right)}^2\cdot 3+{\left(-1\right)}^3\cdot 4+\text{...}+{\left(-1\right)}^{2007}\cdot 2008+{\left(-1\right)}^{2008}\cdot 2009}\end{array}$ összegnek?   2. Igaz-e, hogy $2009+2^{2010}$ prímszám?   3. Hány olyan háromjegyű szám van ‐ a tízes számrendszerben ‐, amelynek a négyzete 2009-re végződik?   4. Az $ABC$ háromszögbe beírható kör a $BC$ oldalt $A_1$-ben, az $AC$ oldalt $B_1$-ben és az $AB$ oldalt $C_1$-ben érinti. Ugyanígy kapjuk az $A_1{B}_1{C}_1$ háromszögből az $A_2{B}_2{C}_2$ háromszöget is. Mekkorák az $ABC$ háromszög szögei, ha szögei ugyanakkorák, mint az $A_2{B}_2{C}_2$ megfelelő szögei ($A$-nál lévő szög megegyezik az $A_2$-nél lévő szöggel, a $B$-nél lévő szög megegyezik a $B_2$-nél lévő szöggel)?   Második forduló   1. Bizonyítsa be, hogy az $\mathrm{1,2,}\text{...}\mathrm{,2010}$ számok közül kiválasztható 1005 úgy, hogy a kiválasztottak szorzata négyzetszám legyen.   2. Hány olyan négyjegyű természetes szám van, amelynek számjegyei között van prímszám és négyzetszám is?   3. Zoli elfelejtette barátja hétjegyű telefonszámát. Bizonyos dolgokra mégis emlékszik: Nem volt benne 0, volt benne legalább két darab 2-es és legalább két darab 3-as, valamint a számjegyek összege éppen 20 volt. Ha mindenképpen fel szeretné hívni barátját, akkor legrosszabb esetben hány telefonszámot kell végig próbálnia?   4. Mennyi a $\sqrt[]{x^2+{\left(y-1608\right)}^2}+\sqrt[]{y^2+{\left(x-1206\right)}^2}$ kifejezés legkisebb értéke, ha $x$ és $y$ valós számok?   5. Hány különböző 10 egységnégyzet területű, egyenlőszárú háromszöget rajzolhatunk a négyzetrácsra úgy, hogy a háromszög egyik oldala rácsvonalra, csúcsai pedig rácspontokra illeszkedjenek? (Két háromszöget akkor tekintünk különbözőnek, ha nem egybevágóak.)   Harmadik (döntő) forduló   1. Mely valós $\left(x;y\right)$ számpárokra teljesül mindkét alábbi egyenlőség? $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x^2+xy}& {\displaystyle =180}\hfill \\ \hfill {\displaystyle y^2+2xy}& {\displaystyle =40}\hfill \end{array}}\}}\end{array}$   2. 60 darab egységkockából egy 3, 4, 5 élhosszúságú téglatestet építettünk. Az egységkockák csúcsai hány olyan téglatestet határoznak meg, amelynek oldallapjai párhuzamosak az eredeti téglatest oldallapjaival?   3. Az alábbi ábrát úgy kaptuk, hogy egy egységsugarú körbe négyzetet szerkesztettünk, majd a négyzet minden oldala, mint átmérő fölé a négyzet belseje felé néző félköröket rajzoltunk. Ezután az ábra bizonyos részeit fehérre, másokat feketére színeztük. Mekkora a feketére színezett rész területe?     II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   Megegyezik az I. kategória első fordulós feladatsorával.   Második forduló   Megegyezik az I. kategória második fordulós feladatsorával.   Harmadik (döntő) forduló   1. Az $ABCD$ paralelogramma $BC$ oldalát a $C$-n túl az oldal hosszával meghosszabbítva az $E$ pontot kapjuk. Az $AE$ szakasz az $F$ pontban metszi a $CD$ oldalt. Az $AF$ szakasz a $H$ pontban metszi a $BD$ átlót és a $BF$ szakasz az $AC$ átlót a $G$ pontban metszi, valamint a $BD$ és $AC$ átlók metszéspontja $O$. Igazolja, hogy az így keletkezett $HOGF$ négyszög területe a paralelogramma területének $\frac{1}{12}$-ed része!   2. 480 darab egységkockából egy 6, 8, 10 élhosszúságú téglatestet építettünk. Az egységkockák csúcsai hány olyan téglatestet határoznak meg, amelynek oldallapjai párhuzamosak az eredeti téglatest oldallapjaival?   3. Igazolja, hogy ha $n$  2-nél nagyobb egész szám, akkor megadható $n$ különböző pozitív egész szám úgy, hogy bármelyik osztója a többi összegének!   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   Megegyezik az I. kategória második fordulós feladatsorával.   Második (döntő) forduló   1. Léteznek-e olyan $t$ és $u$ pozitív egész számok, melyekre $7^t-3^u$ osztható ${10}^{200}$-nal?   2. Jelölje ${\pi }_n$ az első $n$ páratlan prímszám szorzatát és legyen $k$ természetes szám! Igazolja, hogy a ${\left({\pi }_n+1\right)}^{2^k}-1$ számnak legalább $n+k$ különböző prímosztója van!   3. Daraboljon fel egy négyzetet legfeljebb 10 darabra úgy, hogy a darabokból három egybevágó négyzetet lehessen összerakni!   HALADÓK   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Milyen számjegyekből áll a $\underset{\text{2009 darab}}{\overset{}{\underbrace{333\text{...}33}}}\cdot \underset{\text{2009 darab}}{\overset{}{\underbrace{666\text{...}66}}}$ szorzat eredménye?   2. Határozza meg azokat az $abc$ számokat, amelyek egyenlőek az $ab$, $ac$, $ba$, $bc$, $ca$, $cb$ számok összegével! ($a$, $b$, $c$ számjegyek, mindegyik számot a tízes számrendszerben értjük.)   3. Egy hatszög minden szöge egyenlő. Bizonyítsuk be, hogy szemközti oldalainak különbsége megegyezik.   4. Hány olyan $f$ függvény van, amelyről tudjuk, hogy az értelmezési tartománya az $\left\{\mathrm{1,2,}\text{...}\mathrm{,}n\right\}$ halmaz, az értékkészlete a $\left\{\mathrm{2009,2010}\right\}$ halmaz, és az $f\left(1\right)+f\left(2\right)+f\left(3\right)+\text{...}+f\left(n\right)$ összeg páratlan?   5. Az $\left\{1;2;3;4;\text{...};2009\right\}$ számhalmazból 10 darab számot választunk ki egyesével a következő módon: Az első két szám az adott halmaz valamelyik két eleme. A harmadik kiválasztott szám az első kettő összege, ami éppen négyzetszám. Minden további választott szám az addig már kiválasztott számok összege. Hány négyzetszám lehet a kiválasztott 10 darab szám között?   Második forduló   1. Hány olyan pozitív egész számokból álló $\left(x;y\right)$ számpár van, amelyre $\frac{1}{x}-\frac{1}{y}=\frac{1}{2010}$ teljesül?   2. Adott az $ABCD$ paralelogramma. Adjon eljárást a $BC$ oldal azon $X$ pontjának a megszerkesztésére, amin keresztül ha a $BD$ átlóval párhuzamos egyenest húzunk, az egyenes harmadolja a paralelogramma területét! (A szerkesztést nem kell elvégeznie!)   3. Adjunk meg olyan negyedfokú egész együtthatós egyenletet, ahol a főegyüttható 1 és az egyenlet egyik gyöke $\sqrt[]{2}+\sqrt[]{3}$.   4. Tudjuk, hogy az $f\left(x\right)=\frac{p^2}{100}-x^2$ függvény grafikonja és az $x$ tengely által meghatározott síkidomba olyan maximális kerületű téglalap írható, amelynek két csúcsa az $x$ tengelyen, kettő pedig $f\left(x\right)$ grafikonján van rajta. $a)$ Milyen $p$ paraméter esetén létezik a feladatnak megfelelő téglalap? $b)$ Bizonyítsuk be, hogy maximális kerületű téglalap létezése esetén van a téglalapnak olyan csúcsa, amelynek az $f\left(x\right)$ függvény görbéje által meghatározott parabola csúcsától mért távolsága független a $p$ paraméter értékétől!   Harmadik (döntő) forduló   1. 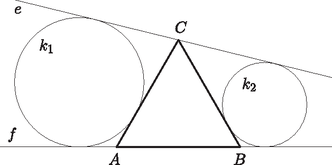Az $ABC$ szabályos háromszög oldalának hossza 10 egység. Az $AB$ oldal egyenese $f$. A $C$ csúcson keresztül olyan $e$ egyenest húztunk, ami a háromszögön kívül halad. Ezután megrajzoltuk az ábrán látható módon a $k_1$ és $k_2$ köröket, amelyek érintik az $e$ és $f$ egyeneseket, továbbá a háromszög egy-egy oldalát kívülről.     Jelölje a körök sugarának hosszát $r_1$ és $r_2$. Bizonyítsuk be, hogy az $r_1+r_2$ összeg értéke nem függ az $e$ egyenes helyzetétől, és határozzuk meg ezt az értéket!   2. Az $x$, $y$, $z$ valós számokra $x+y+z=9$ és $x^2+y^2+z^2=33$ teljesül. Mely $\left(x;y;z\right)$ számhármas esetén lesz az $yz$ szorzat értéke minimális?   3. Az $\left\{1;2;3;\text{...};20\right\}$ halmazból úgy választunk ki maximális számú elemet, hogy a kiválasztott számok közül bármelyik kettőnek a szorzata más-más számjegyre végződjön. Hányféle választás lehetséges?   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   1. Tekintsük azokat a négyjegyű pozitív egész számokat, amelyek számjegyeinek összege 4. Hány százalék az esélye annak, hogy ezek közül egyet véletlenszerűen kiválasztva páros számot kapunk?   2. Bizonyítsuk be, hogy 9 darab egymást követő egész szám négyzetének összege $a)$ nem lehet prímszám, $b)$ nem lehet négyzetszám.   3. Bergengóciában a térképek kicsit eltérnek a megszokottól. A térképen feltüntetik, hogy milyen hosszú utak kötik össze a városokat, ez minden esetben pozitív egész szám kilométerekben megadva. De csatolnak a térképhez egy táblázatot is, ahol feltüntetik, hogy két város közt utakon haladva ‐ akár más városokon keresztül ‐ milyen hosszú a legrövidebb út. Azt azonban nem közlik, hogy ez a legrövidebb út merre, közvetlenül vagy milyen városokon keresztül megy. 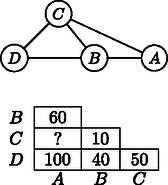A következő ábra egy bergengóc térképet mutat, de hiányoznak róla a városokat összekötő utak hosszai. Azonban megvan a legrövidebb utak táblázata, bár az is hiányosan.       Milyen szám állhat a kérdőjel helyén?   4. Az $x$ és $y$ pozitív egész számra $\begin{array}{c}{\displaystyle \frac{1}{\sqrt[]{y-\sqrt[]{y^2-1}}}-\frac{1}{\sqrt[]{y+\sqrt[]{y^2-1}}}=x}\end{array}$ teljesül. Mi lehet az $y$ szám utolsó számjegye?   5. Mekkora annak a legkisebb szabályos háromszögnek az oldala, amelybe egy 2, egy 3 és egy 4 sugarú kör fedés nélkül beírható?   Második forduló   1. Egy derékszögű háromszög oldalainak hossza és területének mérőszáma is egész szám. Bizonyítsuk be, hogy a beírt kör sugarának hossza is egész szám!   2. Határozza meg a $p$ paraméter értékét úgy, hogy az $x^2+2px-3p-2=0$ egyenlet $x_1$ és $x_2$ gyökeire $x_1^2+x_1^3=4-\left(x_2^2+x_2^3\right)$ teljesüljön.   3. Az $1^{\circ }\mathrm{,}{2}^{\circ }\mathrm{,}{3}^{\circ }\mathrm{,}\text{...}\mathrm{,}{179}^{\circ }$ nagyságú szögekből hányféle módon lehet kiválasztani hármat úgy, hogy a kiválasztott szögek egy különböző oldalú háromszög szögei lehessenek?   4. Az $ABC$ egyenlő szárú háromszög $AB$ alapjának egyik belső pontja $P$. Az $AC$ szár $C$-hez közelebbi harmadolópontja $H$. Az $A$ csúcs $HP$ egyenesre vonatkozó tükörképe a $BC$ oldal $B$-hez közelebbi negyedelőpontja. Határozzuk meg az $AP:PB$ arány értékét!   Harmadik (döntő) forduló   1. Egy derékszögű háromszög egyik oldalához hozzáírt körének sugara a háromszög egyik oldalának hosszával egyezik meg. Igazoljuk, hogy a háromszög valamelyik oldala a másik két oldal számtani közepe.   2. Az $x$, $y$, $z$ valós számokra $x+y+z=9$ és $x^2+y^2+z^2=33$ teljesül. Melyek azok az $\left(x;y;z\right)$ számhármasok, amelyekre az $yz$ szorzat értéke a lehető legnagyobb, illetve a lehető legkisebb?   3. Tekintsük az $y=x^2$ függvény grafikonját, és ezen vegyünk fel három rácspontot: $A$-t, $B$-t és $C$-t! (Rácspont: mindkét koordinátája egész.) Lehet-e az így meghatározott háromszög területe 2010?   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   1. Bizonyítsuk be, hogy egy pitagoraszi számhármasnak mindig van két olyan eleme, amelyek négyzetének különbsége osztható 7-tel. (Pitagoraszi számhármason három olyan $a$, $b$, $c$ természetes számot értünk, amelyekre teljesül az $a^2+b^2=c^2$ összefüggés.)   2. Melyek azok a pozitív egész számok, amelyek 2010-zel nagyobbak számjegyeik négyzetösszegénél?   3. Az $a$, $b$, $x$, $y$ valós számokra teljesülnek a következő összefüggések: $ax+by=3$, $a{x}^2+b{y}^2=7$, $a{x}^3+b{y}^3=16$ és $a{x}^4+b{y}^4=42$. Határozzuk meg $a{x}^5+b{y}^5$ értékét!   4. $ABCD$ trapézban $AB$ párhuzamos $CD$-vel. Jelölje $E$ az $AD$ egyenes és a $BCD$ háromszög köré írt kör $D$-től különböző metszéspontját, $F$ pedig az $AD$ egyenes és a $C$-ből $BE$-hez húzott párhuzamos egyenes metszéspontját. ($D$ az $A$ és az $E$ pont között van.) Bizonyítsuk be, hogy a $BC$ szakasz az $AD$ és $EF$ szakaszok mértani közepe!   5. Legyen $e_n$ a következő módon definiált egyenes: $\begin{array}{c}{\displaystyle e_n:y=\frac{6\left(n-x\right)}{n\left(n+1\right)\left(n+2\right)}n\in \text{N}\setminus \left\{0\right\}\mathrm{.}}\end{array}$ Legyen $H_n$ az $e_n$ egyenes, az $x$-tengely és az $y$-tengely által meghatározott háromszög, és legyen $U_n$ a $H_1\mathrm{,}{H}_2\mathrm{,}\text{...}\mathrm{,}{H}_n$ háromszögek egyesítésével kapott sokszög. Mekkora az $U_{2010}$ területe?   Második (döntő) forduló   1. Egy kör kerületén adott $n$ darab pont ($n\ge 3$). Bármely két pontot összekötő szakaszt ki kell színezni valamilyen (de egyféle) színűre. Legalább hány színre van szükség, ha a közös végpont nélküli szakaszok színe nem lehet azonos?   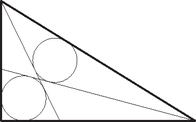2. Egy derékszögű háromszöget úgy bontottunk fel az ábrán látható módon négy részre, hogy a négyszög alakú részbe kör írható, aminek sugara megegyezik a háromszög alakú részbe írt kör sugarával.     Fejezzük ki a körök sugarát a háromszög oldalaival!   3. Tekintsük a koordinátarendszerben a $\left(0;0\right)$, $\left(0;n\right)$, $\left(n;0\right)$, és az $\left(n;n\right)$ ($n$: pozitív egész) csúcspontok által meghatározott négyzetet. Hány olyan négyzet van, amelynek mind a négy csúcspontja a fenti négyzet belső, vagy határon lévő ${\left(n+1\right)}^2$ darab rácspontja közül való? (Rácspont: mindkét koordinátája egész.)