Kezdőlap


Cím:	Összetett rezgések I. rész
Szerző(k):	Vigh Máté
Füzet:	2012/január, 38 - 47. oldal	PDF \| MathML
Témakör(ök):	Csatolt rezgések

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Összetett rezgések
I. rész

Bevezetés

A középiskolában általában nincs lehetőség a rezgőmozgások mélyebb tárgyalására, legtöbbször csak az egyszerű harmonikus rezgés ismertetésére kerül sor. Ennek oka nem csak az idő szűkében rejlik, hanem abban is, hogy a bonyolultabb összetett rezgések szokásos tárgyalása a középiskolai tananyagon jócskán túlnyúló, lineáris algebrai ismereteket igényel (mátrixok sajátértékproblémája). A környezetünkben túlnyomórészt ezekkel az összetett rezgésekkel találkozunk: a pohár koccanása, a tortazselé remegése, a kristályokban a rácsionok nyüzsgése mind-mind összetett rezgés, amelyek nem érthetők meg pusztán az egyszerű harmonikus rezgőmozgásra vonatkozó ismeretekkel.
Ez a kétrészes cikk kísérletet tesz arra, hogy nehéz matematikai apparátus nélkül, egyszerű példákon keresztül, középiskolások számára is érthető módon tárgyalja az összetett rezgéseket és a témához kapcsolódó olyan érdekes jelenségeket, mint a csatolt ingák rezgése vagy a lebegés.

Az egyszerű harmonikus rezgőmozgás

Elevenítsük fel először a harmonikus rezgésre vonatkozó ismereteket a következő egyszerű példán keresztül!

1. példa. Függőleges falból vízszintesen egy egyenes, hosszú, merev huzal áll ki. A huzalra

m

tömegű gyöngy van felfűzve. A gyöngyöt

D

direkciós erejű húzó-nyomó rugó kapcsolja a falhoz (1. ábra).

A kezdetben álló gyöngyöt

v_{0}

kezdeti sebességgel elindítjuk. Írjuk le a mozgást! (A gyöngy súrlódásmentesen csúszhat a huzalon.)

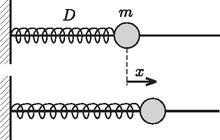1. ábra

Megoldás. A gyöngyre ható függőleges irányú erők kiegyenlítik egymást, vízszintesen pedig csak a rugóerő hat, így a mechanika alapegyenlete az

\begin{matrix} m a (t) = - D x (t) \end{matrix}

alakot ölti, ahol

x (t)

a gyöngy egyensúlyi helyzettől mért (időtől függő) kitérése,

a (t)

a gyorsulása, a negatív előjel pedig arra utal, hogy a gyorsulás mindig a kitéréssel ellentétes irányú. Az egyszerűség kedvéért a fizikai mennyiségek változási gyorsaságát¹ jelöljük a fizikai mennyiség fölé írt ponttal, azaz legyen a gyöngy sebessége

v (t) = \dot{x} (t)

, a gyorsulása pedig

a (t) = \ddot{x} (t)

! A mozgásegyenletet átrendezve az

\begin{matrix} \ddot{x} (t) = - ω^{2} x (t) \end{matrix}

(1)

alakú egyenletre jutunk, ahol bevezettük az

ω = \sqrt[]{D / m}

jelölést. Az (1) egyenlet egy másodrendű differenciálegyenlet a gyöngy kitérésének

x (t)

időfüggésére, melyet szerencsére nem kell tudnunk megoldani, hiszen a megoldása a jól ismert

\begin{matrix} x (t) = A sin (ω t + φ_{0}) \end{matrix}

(2)

formát ölti, a gyöngy sebességét pedig a deriválással (vagy a mechanikai energiamegmaradásból) kapható

\begin{matrix} \dot{x} (t) = A ω cos (ω t + φ_{0}) \end{matrix}

(3)

kifejezés adja meg, ahol

ω

a rezgés fent bevezetett körfrekvenciája,

A

a rezgés amplitúdója (legnagyobb kitérése),

φ_{0}

pedig a rezgés kezdőfázisa. Utóbbi kettő a kezdeti feltételektől függ, vagyis a gyöngy kezdeti kitéréséből és sebességéből kiszámítható.
A konkrét példánkban kezdetben a gyöngy az egyensúlyi helyzetben volt (

x (0) = 0

), ezért a

φ_{0}

kezdőfázis értéke zérus. A kezdősebesség nagysága

\dot{x} (0) = A ω = v_{0}

volt, így a mozgás amplitúdójának nagysága

A = v_{0} / ω

. A feladatbeli kezdőfeltételek esetén tehát a gyöngyszem mozgását az

\begin{matrix} x (t) = \frac{v_{0}}{ω} sin (ω t) \end{matrix}

összefüggés írja le.

Két, rugóval összekötött tömegpont mozgása

Az első példánál egy fokkal bonyolultabb a rugóval összekötött két tömegpont mozgása, amely jól ismert a fizikaversenyekre járók körében. A probléma szokásos megoldási módja a következő: A tömegközéppont egyenletesen haladó mozgását leválasztjuk úgy, hogy beleülünk a tömegközépponttal együtt mozgó koordinátarendszerbe. Itt a rugónak a rendszer tömegközéppontjával egybeeső pontja áll, ezért az egyes testek úgy mozognak, mintha a tömegközéppont által kettéosztott rugó hozzájuk közelebb eső darabja mozgatná őket. Ezzel a gondolattal meghatározható a rezgés körfrekvenciája. Itt azonban egy másik, a bonyolultabb rendszerek esetén is járható utat választunk a megoldáshoz.

2. példa. Egy egyenes, hosszú, vízszintes, merev huzalra

m

és

M

tömegű gyöngyök vannak felfűzve. A gyöngyöket

D

direkciós erejű húzó-nyomó rugó kapcsolja össze (2. ábra). A kezdetben álló rendszert az

m

tömegű gyöngynek adott

v_{0}

kezdeti sebességgel elindítjuk. Írjuk le a mozgást! (A gyöngyök súrlódásmentesen csúszhatnak a huzalon.)

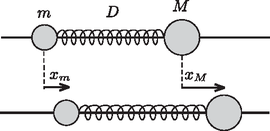2. ábra

Megoldás. Jelöljük az

m

tömegű gyöngy kezdeti helyzettől mért elmozdulását

x_{m}

-mel, az

M

tömegű gyöngy elmozdulását pedig

x_{M}

-mel! Az egyes testekre vízszintesen csak a rugóerő hat, így a gyöngyök mozgásegyenletei:

\begin{matrix} m {\ddot{x}}_{m} & = D (x_{M} - x_{m}), & (4) \\ M {\ddot{x}}_{M} & = - D (x_{M} - x_{m}) . \end{matrix}

Ezek szembeötlően nem az (1) egyenlethez hasonló kifejezések, azaz a testek mozgása nem egyszerűen harmonikus rezgőmozgás. A további vizsgálódás kedvéért osszuk el az egyenletet a tömegekkel, majd adjuk hozzá az első egyenlethez a második

α

-szorosát (ahol

α

valós szám)! Az eredmény:

\begin{matrix} {\ddot{x}}_{m} + α {\ddot{x}}_{M} = - (\frac{D}{m} - α \frac{D}{M}) (x_{m} - x_{M}) . \end{matrix}

(5)

Vezessük be az eredeti koordináták lineáris kombinációjaként² képzett

\begin{matrix} y (t) = x_{m} (t) + α x_{M} (t) \end{matrix}

mennyiséget! A változási gyorsaság képzési szabályából következik, hogy az

y (t)

mennyiség ,,gyorsulása'' a gyöngyök gyorsulásaival hasonlóan egyszerű kapcsolatban van:

\begin{matrix} \ddot{y} (t) = {\ddot{x}}_{m} (t) + α {\ddot{x}}_{M} (t) . \end{matrix}

Az új

y (t)

változó bevezetésével észrevehetjük, hogy az (5) egyenlet

α = M / m

vagy

- 1

esetén

\begin{matrix} \ddot{y} (t) = - ω^{2} y (t) \end{matrix}

alakúra hozható, ahol

\begin{matrix} ω = \sqrt[]{\frac{D}{m} - α \frac{D}{M}} . \end{matrix}

Tehát a két lehetséges lineárkombináció és a hozzájuk tartozó körfrekvencia:

\begin{matrix} y_{1} (t) & = x_{m} (t) + \frac{M}{m} x_{M} (t), & ω_{1} = 0, & (6) \\ y_{2} (t) & = x_{m} (t) - x_{M} (t), & ω_{2} = \sqrt[]{D \frac{m + M}{m M}} . \end{matrix}

y_{1} (t)

lineárkombináció egy zérus frekvenciájú rezgés egyenletét elégíti ki, vagyis

{\ddot{y}}_{1} (t) = 0

. Ez éppen az egyenletes (tehát nulla gyorsulású) mozgás egyenlete, aminek megoldása

\begin{matrix} y_{1} (t) = y_{1} (0) + V t, \end{matrix}

ahol

y_{1} (0)

-t és

V

-t a kezdeti feltételek határozzák meg. Az

y_{2} (t)

lineárkombináció egy

ω_{2}

körfrekvenciájú harmonikus rezgőmozgás egyenletét elégíti ki, így

y_{2} (t)

és

{\dot{y}}_{2} (t)

időfüggése a (2) és (3) összefüggéseknek megfelelően

\begin{matrix} y_{2} (t) & = A sin (ω_{2} t + φ_{0}), \\ {\dot{y}}_{2} (t) & = A ω_{2} cos (ω_{2} t + φ_{0}), \end{matrix}

ahol az amplitúdót és a kezdőfázist most is a kezdeti feltételek határozzák meg.
Vajon milyen kapcsolatban vannak az

y_{1} (t)

és

y_{2} (t)

lineárkombinációk az

m

és

M

tömegű gyöngyök mozgásával?

Nincs más dolgunk, mint

y_{1} (t)

és

y_{2} (t)

ismeretében megoldani a (6) egyenletrendszert

x_{m} (t)

-re és

x_{M} (t)

-re. Így a gyöngyök mozgását leíró egyenletek:

\begin{matrix} x_{m} (t) & = \frac{m}{m + M} y_{1} (t) + \frac{M}{m + M} y_{2} (t), & (7) \\ x_{M} (t) & = \frac{m}{m + M} y_{1} (t) - \frac{m}{m + M} y_{2} (t) . \end{matrix}

További kérdés, hogy van-e fizikai jelentése az

y_{1} (t)

és

y_{2} (t)

lineárkombinációknak? A (7) egyenletekből leolvasható, hogy

$•$	ha $y_{1} (t) \neq 0$ és $y_{2} (t) = 0$ , a két test kitérése minden időpillanatban megegyezik, így a testek rezgés nélkül tisztán haladó mozgást végeznek. Az $y_{1} (t)$ tehát a testek egyenletes haladó mozgását írja le.

$•$	ha $y_{2} (t) \neq 0$ és $y_{1} (t) = 0$ , a két test kitérése minden időpillanatban ellentétes irányú, nagyságuk pedig fordítottan arányos a gyöngyök tömegével, így ebben az esetben a rendszer tömegközéppontja áll. $y_{2} (t)$ a gyöngyök egymáshoz viszonyított rezgőmozgását írja le.

Most térjünk vissza a konkrét példánk megoldásához! Az általános megoldásokat illesztenünk kell a kezdeti feltételekhez. Kezdetben mindkét gyöngy elmozdulása zérus, tehát

x_{m} (0) = x_{M} (0) = 0

, azaz a rezgés kezdőfázisa nulla. Az indítás pillanatában az

m

tömegű test sebessége

v_{0}

, az

M

tömegű test pedig áll, így

{\dot{x}}_{m} (0) = v_{0}

és

{\dot{x}}_{M} (0) = 0

. (6) felhasználásával

{\dot{y}}_{1} (0) = V = v_{0}

és

{\dot{y}}_{2} (0) = v_{0}

adódik. Az

y_{1} (t)

és

y_{2} (t)

lineárkombinációk időfüggése tehát:

\begin{matrix} y_{1} (t) & = v_{0} t, & (8) \\ y_{2} (t) & = \frac{v_{0}}{ω_{2}} sin (ω_{2} t) . \end{matrix}

Ezeket beírva a (7) egyenletekbe:

\begin{matrix} x_{m} & = \frac{m}{m + M} v_{0} t + \frac{M}{m + M} \frac{v_{0}}{ω_{0}} sin (ω_{2} t), \\ x_{M} & = \frac{m}{m + M} v_{0} t - \frac{m}{m + M} \frac{v_{0}}{ω_{0}} sin (ω_{2} t) . \end{matrix}

Végül tehát előzetes várakozásainknak megfelelő eredményt kaptunk: a testek olyan összetett mozgást végeznek, melyben a rendszer tömegközéppontja (az impulzusmegmaradás értelmében)

v_{0} m / (m + M)

sebességgel egyenletesen halad, valamint a testek

ω_{2}

körfrekvenciával rezegnek a tömegközéppont körül. Ha az

m / M

tömegarány nagyon kicsi, akkor az

M

tömegű gyöngy lényegében állónak tekinthető és az

m

tömegű test mozgására visszakapjuk az 1. példa eredményeit.

Három, rugóval összekötött tömegpont mozgása

Az előbb megismert módszert alkalmazzuk most három testből és két rugóból álló rendszer rezgéseinek leírására. Legyen a konkrét feladat a következő:

3. példa. Egy egyenes, hosszú, vízszintes, merev huzalra három azonos

m

tömegű gyöngy van felfűzve. A középső gyöngyöt egy-egy

D

direkciós erejű, egyforma húzó-nyomó rugó kapcsolja a két szélsőhöz (3. ábra).

A kezdetben álló rendszert a bal szélső gyöngynek adott

v_{0}

kezdeti sebességgel elindítjuk. Írjuk le a mozgást! (A gyöngyök súrlódásmentesen csúszhatnak a huzalon.)

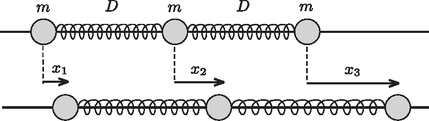3. ábra

Megoldás. Jelöljük a bal szélső gyöngy elmozdulását

x_{1}

-gyel, a középsőét

x_{2}

-vel, a jobb szélsőét pedig

x_{3}

-mal! Az egyes rugók megnyúlása

x_{2} - x_{1}

és

x_{3} - x_{2}

, így a három gyöngyre a mozgásegyenletek:

\begin{matrix} m {\ddot{x}}_{1} & = D (x_{2} - x_{1}), & (9) \\ m {\ddot{x}}_{2} & = - D (x_{2} - x_{1}) + D (x_{3} - x_{2}), \\ m {\ddot{x}}_{3} & = - D (x_{3} - x_{2}) . \end{matrix}

Bevezetve az

ω_{0} = \sqrt[]{D / m}

jelölést és rendezve:

\begin{matrix} {\ddot{x}}_{1} & = ω_{0}^{2} (x_{2} - x_{1}), & (10) \\ {\ddot{x}}_{2} & = ω_{0}^{2} (x_{1} - 2 x_{2} + x_{3}), \\ {\ddot{x}}_{3} & = ω_{0}^{2} (x_{2} - x_{3}) . \end{matrix}

Ezek az egyenletek (akárcsak a két testből álló rendszernél) most sem hasonlítanak a szokásos harmonikus rezgés mozgásegyenletére, de látni fogjuk, hogy az

x_{1}

x_{2}

és

x_{3}

koordinátákból megfelelő lineáris kombinációval most is kikeverhető olyan

y (t)

mennyiség (nem is egy, hanem három), melynek időbeli változását a harmonikus rezgés (1) egyenlete írja le. Keressük tehát azokat az

α

és

β

együtthatókat, melyekkel az

\begin{matrix} y (t) = x_{1} (t) + α x_{2} (t) + β x_{3} (t) \end{matrix}

(11)

módon az eredeti koordinátákból képzett lineáris kombináció időfüggése harmonikus, azaz teljesíti az

\begin{matrix} \ddot{y} (t) = - ω^{2} y (t) \end{matrix}

(12)

egyenletet. Ehhez szorozzuk meg a (10) összefüggések közül a másodikat

α

-val, a harmadikat pedig

β

-val, majd adjuk össze az egyenleteket!

\begin{matrix} {\ddot{x}}_{1} + α {\ddot{x}}_{2} + β {\ddot{x}}_{3} = ω_{0}^{2} ((x_{2} - x_{1}) + α (x_{1} - 2 x_{2} + x_{3}) + β (x_{2} - x_{3})) . \end{matrix}

Rendezve:

\begin{matrix} {\ddot{x}}_{1} + α {\ddot{x}}_{2} + β {\ddot{x}}_{3} = ω_{0}^{2} ((α - 1) x_{1} + (1 - 2 α + β) x_{2} + (α - β) x_{3}) . \end{matrix}

Látható, hogy ha

α = β = 1

, akkor az egyenlet jobb oldala eltűnik, azaz a koordináták

\begin{matrix} y_{1} (t) = x_{1} (t) + x_{2} (t) + x_{3} (t) \end{matrix}

lineárkombinációja egy

ω_{1} = 0

körfrekvenciájú

{\ddot{y}}_{1} (t) = 0

alakú ,,rezgési egyenletet'' elégít ki. Ez azt jelenti, hogy az

y_{1} (t)

mennyiség az idő függvényében egyenletesen változik, azaz

\begin{matrix} y_{1} (t) = y_{1} (0) + V t, \end{matrix}

ahol

V

egy sebesség dimenziójú állandó (lényegében a testek kezdősebességeinek összege). Hasonlóan a 2. példa megoldásához, látni fogjuk, hogy ez a lineárkombináció írja le a rendszer tömegközéppontjának mozgását.
A továbbiakban tegyük fel, hogy

α \neq 1

! Azért, hogy a (12) egyenlettel azonos alakú időfüggést kapjunk, végezzük el a következő kiemelést:

\begin{matrix} {\underset{︸}{{\ddot{x}}_{1} + α {\ddot{x}}_{2} + β {\ddot{x}}_{3}}}_{\ddot{y} (t)}^{} = - {\underset{︸}{(1 - α) ω_{0}^{2}}}_{ω^{2}}^{} {\underset{︸}{(x_{1} + \frac{1 - 2 α + β}{α - 1} x_{2} + \frac{α - β}{α - 1} x_{3})}}_{y (t)}^{} . \end{matrix}

(13)

Innen leolvasható, hogy a harmonikus időfüggés teljesüléséhez az együtthatók között a következő összefüggéseknek kell fennállniuk:

\begin{matrix} α = \frac{1 - 2 α + β}{α - 1}, β = \frac{α - β}{α - 1}, \end{matrix}

(14)

a körfrekvencia pedig (13) szerint

\begin{matrix} ω = ω_{0} \sqrt[]{1 - α} . \end{matrix}

(15)

A (14) egyenletrendszer így is írható:

\begin{matrix} (α + 2) (α - 1) = β - 1, α (β - 1) = 0. \end{matrix}

Ennek két megoldása van:

\begin{matrix} α & = 0, & β & = - 1; \\ α & = - 2, & β & = 1. \end{matrix}

A korábban talált

y_{1} (t)

mellett megkaptuk tehát az

x_{1}

x_{2}

x_{3}

koordináták további két olyan lineárkombinációját, amelyek az időben (12) szerint harmonikusan változnak. Tehát a három független lineárkombináció (és a nekik megfelelő rezgési frekvencia) a következő:

\begin{matrix} y_{1} (t) & = x_{1} (t) + x_{2} (t) + x_{3} (t), & ω_{1} = 0, & (16) \\ y_{2} (t) & = x_{1} (t) - x_{3} (t), & ω_{2} = ω_{0}, \\ y_{3} (t) & = x_{1} (t) - 2 x_{2} (t) + x_{3} (t), & ω_{3} = \sqrt[]{3} ω_{0} . \end{matrix}

Ezek időfüggése pedig:

\begin{matrix} y_{1} (t) & = y_{1} (0) + V t, & (17) \\ y_{2} (t) & = A_{2} sin (ω_{2} t + φ_{2}), \\ y_{3} (t) & = A_{3} sin (ω_{3} t + φ_{3}) . \end{matrix}

y_{1} (0)

és

V

értéke, az

A_{2}

A_{3}

amplitúdók és a

φ_{2}

φ_{3}

kezdőfázisok a kezdeti feltételekből (azaz a kiinduló koordinátákból és sebességekből) határozhatók meg. A feladatunk most is az

x_{1} (t)

x_{2} (t)

és

x_{3} (t)

kitérés-idő függvények meghatározása. A (16) egyenlet alapján ezek kifejezhetők az ismert időfüggésű

y_{1} (t)

y_{2} (t)

y_{3} (t)

mennyiségekkel:

\begin{matrix} x_{1} (t) & = \frac{1}{3} y_{1} (t) + \frac{1}{2} y_{2} (t) + \frac{1}{6} y_{3} (t), & (18) \\ x_{2} (t) & = \frac{1}{3} y_{1} (t) - \frac{1}{3} y_{3} (t), \\ x_{3} (t) & = \frac{1}{3} y_{1} (t) - \frac{1}{2} y_{2} (t) + \frac{1}{6} y_{3} (t) . \end{matrix}

A két testből álló rendszerhez hasonlóan könnyen kideríthetjük, hogy mi az

y_{i} (t)

(

i = 1,2,3

) lineárkombinációk fizikai jelentése (4. ábra). A (18) összefüggésből látható, hogy ha

$•$	$y_{1} (t) \neq 0$ és $y_{2} (t) = y_{3} (t) = 0$ , akkor $x_{1} (t) = x_{2} (t) = x_{3} (t)$ , azaz mindhárom test kitérése megegyezik: ilyenkor a rendszer nem rezeg, ez a lineárkombináció a tisztán haladó mozgást írja le.

•

y_{2} (t) \neq 0

és

y_{1} (t) = y_{3} (t) = 0

, akkor

x_{1} (t) = - x_{3} (t)

és

x_{2} (t) = 0

, vagyis az

y_{2} (t)

lineárkombináció olyan ,,lélegző'' mozgásformát ír le, melyben a középső test áll, a két szélső test kitérése pedig minden időpillanatban ellentétes, egyenlő nagyságú. A rendszer tömegközéppontja ilyenkor áll.

•

y_{3} (t) \neq 0

és

y_{1} (t) = y_{2} (t) = 0

, akkor

x_{1} (t) = x_{3} (t) = - \frac{1}{2} x_{2} (t)

, ami olyan ,,tili-toli'' mozgásformát jelent, hogy a két szélső test kitérése minden időpillanatban megegyezik, a középső pedig velük ellentétesen, kétszer akkora kitéréssel mozog. A tömegközéppont ebben az esetben sem mozog.

4. ábra.Az

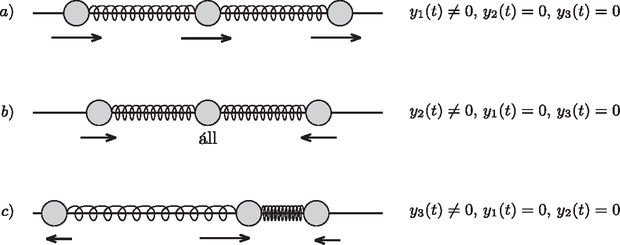y_{i} (t)

(

i = 1,2,3

) lineárkombinációk fizikai jelentésének szemléltetése:

y_{1} (t)

az egyenletes mozgást

(a)

y_{2} (t)

a lüktető mozgást

(b)

y_{3} (t)

pedig a ,,tili-toli'' mozgást

(c)

írja le. A rendszer mozgása e három mozgásforma kezdőfeltételektől függő, megfelelő arányú szuperpozíciójaként (keverékeként) állítható elő

Hátra van még a konkrét példánk megoldása, azaz a (18) általános megoldások illesztése a kezdeti feltételekhez. Kezdetben mindhárom test egyensúlyi helyzetben volt, így

x_{1} (0) = x_{2} (0) = x_{3} (0) = 0

. Csak a bal oldali testet löktük meg

v_{0}

kezdősebességgel, így

{\dot{x}}_{1} (0) = v_{0}

{\dot{x}}_{2} (0) = {\dot{x}}_{3} (0) = 0

. Ezekből és a (16) egyenletekből következik, hogy

y_{1} (0) = y_{2} (0) = y_{3} (0) = 0

(azaz

φ_{2} = φ_{3} = 0

) és

{\dot{y}}_{1} (0) = {\dot{y}}_{2} (0) = {\dot{y}}_{3} (0) = v_{0}

. A (17) összefüggéseket figyelembe véve

V = v_{0}

A_{2} ω_{2} = v_{0}

A_{3} ω_{3} = v_{0}

. A testek mozgását leíró egyenletek tehát:

\begin{matrix} x_{1} (t) & = \frac{1}{3} v_{0} t + \frac{1}{2} \frac{v_{0}}{ω_{0}} sin (ω_{0} t) + \frac{1}{6} \frac{v_{0}}{\sqrt[]{3} ω_{0}} sin (\sqrt[]{3} ω_{0} t), & (19) \\ x_{2} (t) & = \frac{1}{3} v_{0} t - \frac{1}{3} \frac{v_{0}}{\sqrt[]{3} ω_{0}} sin (\sqrt[]{3} ω_{0} t), \\ x_{3} (t) & = \frac{1}{3} v_{0} t - \frac{1}{2} \frac{v_{0}}{ω_{0}} sin (ω_{0} t) + \frac{1}{6} \frac{v_{0}}{\sqrt[]{3} ω_{0}} sin (\sqrt[]{3} ω_{0} t) . \end{matrix}

Az egyes gyöngyök elmozdulását ábrázolhatjuk az idő függvényében, ahogy azt az 5. ábra mutatja az

y_{i} (t)

lineárkombinációk időfüggésével együtt.

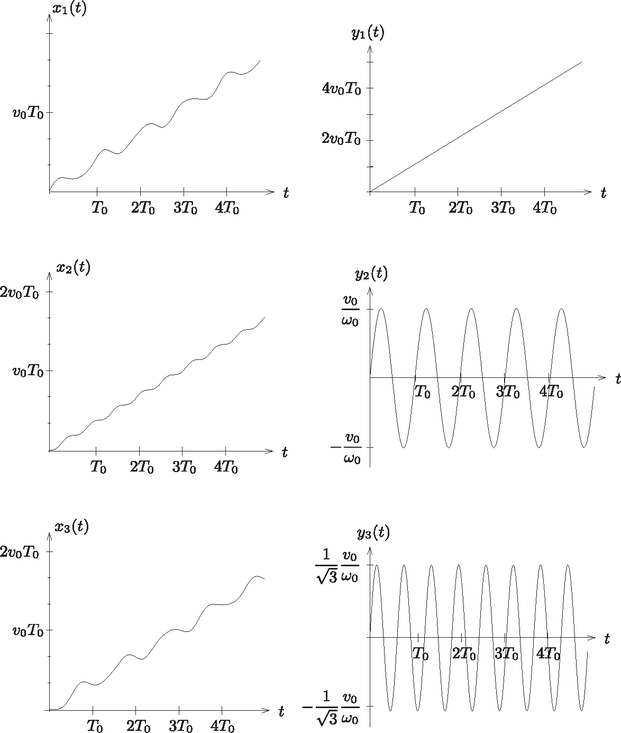5. ábra. Első oszlop: A három test

x_{i}

(

i = 1,2,3

) kitérése az idő függvényében.
Második oszlop: az

x_{i} (t)

kitérésekből képzett

y_{i} (t)

lineárkombinációk.
Az időt

T_{0} = \frac{2 π}{ω_{0}}

egységekben mértük

Általános következtetések

Az előzőekben láttuk, hogy a két és három testből álló rendszerek egyenes mentén történő (egydimenziós) rezgéseinél az egyes testek

x_{i} (t)

koordinátáinak időfüggését leíró egyenletek általában nem hasonlítanak az egyszerű harmonikus rezgőmozgás egyenletére, de a koordinátákból megfelelő lineárkombináció képzésével előállíthatók olyan

y_{i} (t)

mennyiségek, melyek már az időben harmonikusan (egy jellemző körfrekvenciával tisztán szinuszosan) változnak. Az

y_{i} (t)

lineárkombinációk pontos időfüggése a rendszer kezdőfeltételeinek (kezdeti kitérések és sebességek) ismeretében meghatározható, majd abból az egyes testek elmozdulásainak

x_{i} (t)

értéke is megállapítható.
Az eljárás általánosítható nagyobb rendszerekre is. Álljon a rendszerünk

N

tetszőleges tömegű pontszerű testből, melyek egy egyenes mentén mozoghatnak, és a kössék össze a testeket (akár különböző erősségű) rugók! Ha az

i

-edik test kitérését

x_{i} (t)

-vel jelöljük, a rendszer mozgása a következő recepttel írható le:

Felírjuk a rendszer összes elemének mozgásegyenletét, azaz minden

i = 1,2, ..., N

-re egy

\begin{matrix} {\ddot{x}}_{i} (t) = \sum_{j = 1}^{N} η_{j} x_{j} (t) \end{matrix}

alakú egyenletet (itt az

η_{j}

együtthatókat a rugók direkciós ereje és a testek tömegei határozzák meg).

Megkeressük azokat az

α_{1}, α_{2}, ..., α_{N}

együtthatókat, melyekkel a testek kitéréseiből képzett

\begin{matrix} y (t) = \sum_{j = 1}^{N} α_{j} x_{j} (t) \end{matrix}

lineárkombinációk a harmonikus rezgőmozgás

\begin{matrix} \ddot{y} (t) = - ω^{2} y (t) \end{matrix}

egyenletét elégítik ki alkalmas

ω

körfrekvenciával. Általában

N

különböző ilyen

y_{i} (t)

lineárkombinációt fogunk találni (ahol

i = 1,2, ..., N

). Ezekből egy kombinációhoz mindig zérus körfrekvencia tartozik, ez írja le az egyenletesen haladó mozgást.

3.	Az $y_{i} (t)$ lineárkombinációkra vonatkozó rezgési egyenleteket megoldjuk és a megoldásokat illesztjük a kezdeti feltételekhez (kezdősebességek és kezdeti koordináták).

4.	Végül az egyes testek $x_{i} (t)$ koordinátáit kifejezzük az $y_{i} (t)$ mennyiségekkel.

y_{i} (t)

mennyiségeket, vagy általánosabban fogalmazva a rendszer eredeti koordinátáinak olyan lineárkombinációit, amelyek időfüggése tisztán harmonikus (azaz az időnek egyetlen, adott körfrekvenciájú szinuszos függvényével írható le), normálkoordinátáknak, a nekik megfelelő

ω_{i}

körfrekvenciákat pedig a rendszer saját(kör)frekvenciáinak nevezzük. Az olyan mozgásformákat, melyekben egyetlen normálkoordináta kivételével mindegyik zérus, sajátrezgésnek vagy normálrezgésnek nevezzük. Például a 3. példában szereplő gyöngyök az egyenletes, a lüktető és a tili-toli mozgásban sajátrezgéseket végeznek. Minden sajátrezgéshez tartozik egy amplitúdó-konfiguráció (a 3. példában a három sajátrezgéshez az amplitúdók

1 : 1 : 1

1 : 0 : 1

és

1 : (- 2) : 1

aránya tartozott), ezeket normálmódusoknak nevezzük.

\begin{matrix} Vigh Máté \end{matrix}

¹Idő szerinti deriváltját.

²Az $x_{1}, x_{2}, x_{3}, ...$ mennyiségek lineáris kombinációján a $λ_{1} x_{1} + λ_{2} x_{2} + λ_{3} x_{3} + ...$ alakú összeget értjük, ahol $λ_{1}, λ_{2}, λ_{3}, ...$ (most) valós számok.