Kezdőlap


Cím:	How to draw a ``good'' star?
Szerző(k):	Ildikó Miklós
Füzet:	2004/januári melléklet, 9 - 13. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

In problem I. 59. of the informatics section of our 2003 October issue, the task was to draw all possible $n$ -pointed regular star polygons. These are obtained by connecting every $k$ -th vertex of a regular $n$ -gon ( $n \geq 5$ ), starting at one vertex (Figure 1). Only those solutions are accepted that do produce an $n$ -pointed star.

Figure 1

Definition [1]. A regular star polygon consists of a finite number of line segments in the plane where each endpoint is incident to two line segments and there exists an isometry that maps one line segment onto any other one while mapping the polygon into itself. The boundary of a regular polygon is also a figure of this kind but that is not called a regular star polygon. Diagonals of a regular polygon equidistant (with a non-zero distance) from the centre form a regular star polygon.

Consider the regular star obtained by applying the second part of the definition to a regular pentagon (Figure 2a).

Figure 2a

For this star pentagon it is true that there is an isometry for any pair of its edges: they can be mapped onto each other by either a rotation or reflection in a line (Figure 2b). The name pentagon is slightly misleading: the stars of Figures 2 clearly have ten sides.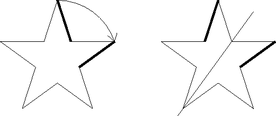

Figure 2b

What further properties do these figures have? The regular star

n

-gon has

2 n

sides, the sides being equal due to the symmetries; all other angles (out of its

2 n

angles) are equal, let the common measure be

α

, and the remaining

n

angles (let them be

β

) are also equal. It is straightforward from the sum of the angles of a polygon that

\begin{matrix} α + β = 360^{\circ} - \frac{360^{\circ}}{n} . \end{matrix}

Let

A_{0}

be the initial vertex of the appropriate regular polygon, let

A_{1}

denote the

k

-th vertex and let

B_{1}

be the vertex next to

A_{0}

(in a clockwise direction). In the triangle

A_{0} A_{1} O

(Figure 3a),

γ = \frac{k}{n} \cdot 360^{\circ}

(since we are dealing with

k

-neighbouring vertices of a regular

n

-gon), thus

\begin{matrix} α = 180^{\circ} - γ = (1 - \frac{2 k}{n}) \cdot 180^{\circ} . \end{matrix}

(1)

In the triangle

A_{0} B_{1} O

\begin{matrix} ∠ A_{0} O B_{1} = \frac{360^{\circ}}{2 n} = \frac{180^{\circ}}{n} = 180^{\circ} - \frac{α}{2} - \frac{β}{2} . \end{matrix}

(2)

Hence

\frac{α}{2} + \frac{β}{2} = 180^{\circ} - \frac{180^{\circ}}{n}

, that is,

α + β = 360^{\circ} - \frac{360^{\circ}}{n}

, a sum independent of

k

. The value of

β

can also be calculated from (1) and (2):

\begin{matrix} β = 180^{\circ} + (k - 1) \frac{360^{\circ}}{n} . \end{matrix}

Figure 3a

Rotational symmetry implies that every other vertex of a star polygon lies on a circle. Let

k_{1}

and

k_{2}

denote these two concentric circles (Figure 3b).

Figure 3b

It seems that every other angle of a star polygon is concave. Is that true? If the radius of the inner circle

k_{2}

is increased (or decreased), the resulting figure will also obey the definition, i.e. it will also be a star polygon but its sides will no longer lie on the diagonals of a regular polygon. The motion of the ``inner'' vertices can be continued until there are no more concave angles and the circle

k_{1}

is not yet reached (when it is reached, a regular

2 n

-gon is formed). This can be done since

\begin{matrix} α + β = 360^{\circ} - \frac{360^{\circ}}{n} < 360^{\circ} (Figure 4a). \end{matrix}

According to the definition this should also be a star polygon but if we do not want it to be, like in the case of the regular polygon, we can require additionally that every other angle of a star polygon should be concave. There is an intermediate state in which

β = 180^{\circ}

and the star polygon then reduces to a regular

n

-gon.

Figure 4a

If the inner circle

k_{2}

is rotated about the centre, rotational symmetry is preserved but the axial symmetry mapping adjacent sides onto each other is destroyed. Thus the resulting ``circular saw'' is not a regular star pentagon (Figure 4b).

Figure 4b

Let us consider now the solutions of the informatics problem obtained by connecting the vertices of a regular

n

-gon to their

k

-th neighbours. That results in a closed polygon whose sides may intersect [1]. (There are solutions to the problem.)
If

k > \frac{n}{2}

then the same diagram can be obtained by connecting each vertex to its

(n - k)

-th neighbour. For

n

even,

k = \frac{n}{2}

will not provide a solution either; the result is a single line segment, a diameter of the circumscribed circle. Thus we can assume that

2 \leq k < \frac{n}{2}

.
Let us first consider the case of

n = 11

(that was the example discussed in the informatics problem).

2 \leq k < 5.5

allows:

k = 2,3,4,5

. If

k = 2

, the vertices in the order of connection are

\begin{matrix} 0, 2, 4, 6, 8, 10, 1, 3, 5, 7, 9, 0. \end{matrix}

(In the 6th step, it would not make sense to write 12 since the 12th vertex coincides with the first one.) We know 11 is prime, so the polygon closes up in the 11th step. The possible cases are shown in Figure 5.

Figure 5

A similar result is obtained for any prime number

n

. Then the possible values of

k

are

k = 2,3, ..., [\frac{n}{2}]

(where

[x]

stands for the greatest integer not greater than

x

). Since

n

is odd,

\frac{n}{2}

is not a whole number, so the number of solutions is

[\frac{n}{2}] - 1

.
If

n = 10

then

2 \leq k < 5

allows

k = 2,3,4

, as shown in Figure 6. In the case of

k = 2

the polygon returns to the starting point in the 5th step without the line segments intersecting each other. A regular pentagon is obtained. We can observe in general that if

k

divides

n

then a regular

\frac{n}{k}

-gon is obtained, which is not accepted as a solution.

Figure 6

In the case of

k = 4

we get a regular five-pointed star which could be a solution but it follows from the wording of the problem that it does not belong here: For

n = 10

we should get ten-pointed stars. In general, if

k

and

n

have common factors, that is, if they are not relative primes, then an

\frac{n}{(n, k)}

-pointed regular star is obtained (where

(n, k)

stands for the greatest common divisor of

n

and

k

), which is not accepted as a solution.
In the case of

k = 3

we do get a ten-pointed star. In general, if

k

and

n

are relative primes (

k \geq 2

) then all vertices can be traversed without returning to the starting point before the

n

-th step. The sides of the polygon will intersect each other, and we get an

n

-pointed star.
Eventually, we only obtained one ``good'' solution for

n = 10

although if the informatics problem were defined as the connecting of diagonals equidistant from the centre, we would have three of them (Figure 7.)

Figure 7

Does the problem always have a solution if

n

is not a prime? For

n = 6

k

can only be 2, which results in a regular triangle, not a solution.
If

n

is least 3 there is a smaller number that is relatively prime to it, for example

n - 1

. However, we are only using values of

k

that are smaller than one half of

n

. For

n = 6

there is no solution since the only number less than 3, one half of 6, that is relatively prime to 6 is 1. Are there any other numbers like that? We will show that there are not.
The next composite number is

n = 8

. A relative prime less than its half is 3. For

n = 9

, 2 is a solution (but so is 4), for

n = 10

, 3 is a solution. Consider now the following product:

\begin{matrix} s_{r} : = p_{1} \cdot p_{2} \cdot ... \cdot p_{r}, \end{matrix}

where

p_{i}

is the

i

-th prime number.

s_{3} = 2 \cdot 3 \cdot 5 = 30

, which is clearly greater than 5 (its largest factor), thus for all

5 < n < 30

there exists

k \in {2,3,5}

such that

(k, n) = 1

. Otherwise all the first three primes would appear among the prime factors of

n

which would mean

n \geq 30

. The generalization is obtained similarly: If

n

is smaller than the product of the first

r

primes then some element of the set

{p_{1}, p_{2}, ..., p_{r}}

is relatively prime to

n

. Thus if

p_{r} < n < s_{r}

then there exists

k \leq p

such that

(k, n) = 1

. In the interval

[5,30]

we have already checked the numbers less than 11. For larger numbers it follows from the above that there is a number less than

\frac{n}{2}

that is relatively prime to

n

since every prime element of the previous set is less than half of 11.
The lower limit of the

r

th interval is the

r

-th prime number and its upper limit which grows much faster then the lower limit, is the product of the first

r

primes. Thus the length of the intervals grows very fast. (E.g. for

r = 4

the interval is

[7,210]

and for

r = 5

it is

[11,2310]

.) From the second step onwards, the upper limit is always multiplied by a prime greater than 2, so there exists an interval for any

n

, containing both

\frac{n}{2}

and

n

. Thus there will always be a prime less than

\frac{n}{2}

in the set of primes corresponding to the interval that is relatively prime to

n

. Hence the informatics problem has at least one solution for every

n > 6

. The number of solutions in general is

\frac{φ (n) - 2}{2}

where

φ (n)

denotes the number of relative primes to

n

that are not greater than

n

. (To see this, observe that

k

and

n

are relative primes precisely when

n - k

and

n

are. On the other hand, if

k = 1

n - 1

then no solution is obtained.) The estimations above imply that

φ (n) > 2

n > 6

.
This result certainly does not mean that a six-pointed star does not exist since we know that well (Figure 8). It is indeed formed by diagonals of a regular hexagon equidistant from the centre. In addition, it is the only polygon of that kind. If we want to get all possible star polygons, the informatics problem should be modified. If the polygon returns to the starting point, a new one should be started from the second vertex, then another one from the third vertex and so on as long as there are ``free'' vertices.

Figure 8

Complicated as the above considerations may seem, a simple program can be written for finding all the numbers that are relatively prime to a given number and are smaller than its half. Then we can obtain our ``good'' stars.

Bibliography

[1]	Hajós, György: Introduction to Geometry, Tankönykiadó (Budapest, 1991).