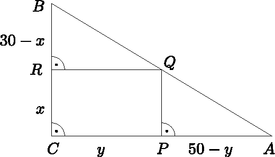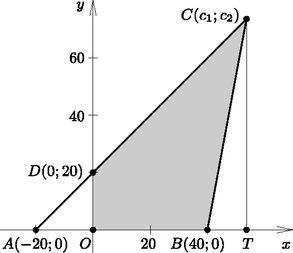Cím:	Megoldásvázlatok a 2010/4. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Benyovics Ágnes
Füzet:	2010/május, 263 - 268. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Egy kocka élének hossza centiméterben mérve egész szám. A kocka felületét pirosra festettük, majd az oldallapjaival párhuzamos vágásokkal 1 cm élű kiskockákra daraboltuk. $a)$ Hány centiméter volt a kocka éle, ha a pontosan egy festett lapú kiskockák száma megegyezik a festetlen kiskockák számával? $b)$ Hány olyan különböző méretű kocka létezik, amelyből 0,5 és 0,6 közé eső valószínűséggel választhatunk ki festetlen kiskockát? (A kiskockák kiválasztásának valószínűségét vegyük egyenlőnek.)  (11 pont)   Megoldás. $a)$ Legyen a kocka éle $x$ cm $\left(x\in {\text{Z}}^{+}\right)$. A festetlen kiskockák száma: ${\left(x-2\right)}^3$. A pontosan egy festett lapú kiskockák száma: $6{\left(x-2\right)}^2$. Tudjuk, hogy $\begin{array}{c}{\displaystyle {\left(x-2\right)}^3=6{\left(x-2\right)}^2\mathrm{,}{\left(x-2\right)}^2\left(x-8\right)=0.}\end{array}$ Az $x_1=2$ nem megoldása a feladatnak. Az $x_2=8$ az egyedüli megoldás. A kocka éle 8 cm. $b)$ Legyen a keresett valószínűség $p$. Tudjuk, hogy $0\mathrm{,}5\le p\le 0\mathrm{,}6$, azaz: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 0\mathrm{,}5\le \frac{{\left(x-2\right)}^3}{x^3}\le 0\mathrm{,}\mathrm{6,}\left(x\in {\text{Z}}^{+}\right)\mathrm{.}}\hfill \\ \hfill {\displaystyle \sqrt[3]{0\mathrm{,}5}\cdot x+2\ge x\ge \sqrt[3]{0\mathrm{,}6}\cdot x+\mathrm{2,}}\hfill \end{array}}$ amiből századpontossággal kapjuk, hogy: $9\mathrm{,}69\le x\le 12\mathrm{,}77$. Tehát az $x$ lehetséges értékei: 10, 11, 12. Vagyis 3-féle megfelelő kocka létezik.   2. Bizonyítsuk be, hogy minden $n$ természetes szám esetén $a)$ az $n^5-5n^3+4n+1$ szám $1$-re végződik; $b)$ $5\mid 2^{4n+1}+3$.  (12 pont)   Megoldás. $a)$ Az $n^5-5n^3+4n+1$ kifejezés pontosan akkor végződik 1-re, ha az $n^5-5n^3+4n$ kifejezés 0-ra végződik, azaz osztható 10-zel. Végezzük el a következő átalakításokat: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle n^5-5n^3+4n}& {\displaystyle =n\left(n^4-5n^2+4\right)=n\left(n^2-1\right)\left(n^2-4\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =n\left(n+1\right)\left(n-1\right)\left(n+2\right)\left(n-2\right)\mathrm{.}}\hfill \end{array}}$ A fenti kifejezés öt egymás utáni természetes szám szorzata, tehát biztosan van a tényezők között 2-vel, illetve 5-tel osztható. Így a kifejezés minden $n$ természetes szám esetén osztható 10-zel. $b)$ A 2 hatványai sorban a következő számokra végződnek: 2, 4, 8, 6, 2, 4, $\text{...}$ stb., vagyis a $4n+1$-edik hatvány mindig 2-re végződik, így a kifejezés utolsó számjegye mindig 5 lesz. Vagyis a kifejezés valóban minden $n$ természetes szám esetén osztható 5-tel.   3. Oldjuk meg a következő egyenlőtlenséget: $\begin{array}{c}{\displaystyle \text{log}{}_{x+3}\left(x^2-9x-10\right)\le \text{log}{}_{x+3}12.}\end{array}$  (14 pont)   Megoldás. Meghatározzuk az egyenlőtlenség értelmezési tartományát. ${\displaystyle \begin{array}{c}\hfill {\displaystyle x^2-9x-10>\mathrm{0,}\left(x+1\right)\left(x-10\right)>\mathrm{0,}\text{azaz}x<-1\cup 10<x\mathrm{.}}\hfill \\ \hfill {\displaystyle x+3>\mathrm{0,}\text{azaz}-3<x\mathrm{.}}\hfill \\ \hfill {\displaystyle x+3\ne \mathrm{1,}\text{azaz}x\ne -2.}\hfill \end{array}}$ Tehát $x\in \left]-3;-2\right[\cup \left]-2;-1\right[\cup \left]10;\infty \right[$. Ha $x\in \left]-3;-2\right[$, akkor a logaritmus függvény csökkenő, ezért: $\begin{array}{c}{\displaystyle x^2-9x-10\ge \mathrm{12,}{x}^2-9x-22\ge \mathrm{0,}\left(x+2\right)\left(x-11\right)\ge \mathrm{0,}}\end{array}$ vagyis: $x\in \left]-\infty ;-2\right]\cup \left[11;\infty \right[$. Tehát ebben az esetben a megoldás: $x\in \left]-3;-2\right[$. Ha $x\in \left]-2;-1\right[$, akkor a logaritmus függvény növekvő, ezért: $\begin{array}{c}{\displaystyle x^2-9x-10\le \mathrm{12,}{x}^2-9x-22\le \mathrm{0,}\left(x+2\right)\left(x-11\right)\le \mathrm{0,}}\end{array}$ vagyis: $x\in \left[-2;11\right]$. Tehát ebben az esetben a megoldás: $x\in \left]-2;-1\right]$. Ha $x\in \left]10;\infty \right[$, akkor a logaritmus függvény növekvő, ezért: $\begin{array}{c}{\displaystyle x^2-9x-10\le \mathrm{12,}}\end{array}$ vagyis: $x\in \left[-2;11\right]$. Tehát ebben az esetben a megoldás: $x\in \left]10;11\right]$. Mindent egybevetve a feladat megoldása: $x\in \left]-3;-2\right[\cup \left]-2;-1\right[\cup \left]10;11\right]$.   4. $a)$ Egy növekvő számtani sorozat első, negyedik és tizedik tagja egy mértani sorozat első három tagja. A számtani sorozat nyolcadik tagja $10$. Határozzuk meg a mértani sorozat első tagját. $b)$ A 3, 4, 5, 6 számjegyekből képezzünk véletlenszerűen egy csupa különböző számjegyből álló négyjegyű számot. Mennyi a valószínűsége annak, hogy a kapott szám $4$-gyel osztható?  (14 pont)   Megoldás. $a)$ Jelöljük a számtani sorozat tagjait $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_n$-nel. Tudjuk, hogy $a_4=a_1+3d$, $a_{10}=a_1+9d$, $a_8=a_1+7d=10$, vagyis $a_1=10-7d$. A mértani sorozat tulajdonsága miatt: $\begin{array}{c}{\displaystyle \frac{a_1+3d}{a_1}=\frac{a_1+9d}{a_1+3d}\mathrm{,}\frac{10-4d}{10-7d}=\frac{10+2d}{10-4d}\mathrm{,}}\end{array}$ amiből kapjuk: $\begin{array}{c}{\displaystyle 30d^2-30d=\mathrm{0,}30d\left(d-1\right)=0.}\end{array}$ Az egyenlet gyökei: $d_1=0$ (ez a feladatnak nem megoldása, mivel a sorozat növekvő), $d_2=1$. Vagyis a mértani sorozat első tagja: $a_1=10-7d=3$. $b)$ A 3, 4, 5, 6 számjegyekből képezhető különböző számjegyekből álló négyjegyű számok száma: $4!=24$. A néggyel osztható számok utolsó két számjegye, mint kétjegyű szám osztható néggyel, így a szóba jöhető számok 36, 56 vagy 64-re végződhetnek. Vagyis a kedvező esetek száma 6 (mert mindhárom esetben a maradék két számjegy kétféleképpen írható a szám elejére). A keresett valószínűség: $\begin{array}{c}{\displaystyle p=\frac{6}{24}=0\mathrm{,}25.}\end{array}$   II. rész     5. Egy derékszögű háromszög alakú saroktelekre téglalap alapterületű házat tervezünk úgy, hogy annak két oldala az utcával párhuzamos legyen. A telek két merőleges oldalának hossza 50 m és 30 m. Hogyan válasszuk meg a ház oldalainak hosszát, ha a lehető legnagyobb alapterületű házat szeretnénk megtervezni?  (16 pont)   Megoldás. Használjuk az ábra jelöléseit. Az $APQ$ és $QRB$ háromszögek hasonlósága miatt fennáll a következő aránypár: $\begin{array}{c}{\displaystyle \frac{30-x}{x}=\frac{y}{50-y}\mathrm{.}}\end{array}$ Rendezve az egyenlőséget: $\begin{array}{c}{\displaystyle y=\frac{150-5x}{3}\mathrm{.}}\end{array}$     A maximális területű téglalapot keressük: $\begin{array}{c}{\displaystyle t\left(x\right)=xy=\frac{x\left(150-5x\right)}{3}=-\frac{5}{3}{x}^2+50x\mathrm{.}}\end{array}$ Keressük a $t\left(x\right)$ másodfokú függvény szélsőértékét. A függvény zérushelyei: $x_1=0$, $x_2=30$. A másodfokú függvény képének szimmetriája miatt a szélsőérték $x=15$-nél van. Mivel a főegyüttható negatív, ezért itt maximuma van. Vagyis a ház oldalainak hossza: $x=15$ m, $y=25$ m.   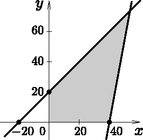6. A derékszögű koordinátarendszer első síknegyedéből az ábrán látható két egyenes egy $2010$ egység területű négyszöget vág le.     $a)$ Határozzuk meg a két egyenes metszéspontjának koordinátáit. $b)$ Írjuk fel az egyenesek egyenletét.  (16 pont)   Megoldás. Az ábra jelöléseit használjuk. Tudjuk, hogy: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t_{ABC}}& {\displaystyle =\frac{60\cdot c_2}{2}=30\cdot c_2\mathrm{,}}\hfill \\ \hfill {\displaystyle t_{AOD}}& {\displaystyle =\frac{20\cdot 20}{2}=\mathrm{200,}}\hfill \\ \hfill {\displaystyle t_{OBCD}}& {\displaystyle =t_{ABC}-t_{AOD}=30\cdot c_2-200=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2010.}\hfill \end{array}}$ Vagyis: $c_2=\frac{221}{3}$.     Mivel $ATC$ egyenlőszárú derékszögű háromszög, így $AT=CT$, azaz $20+c_1=\frac{221}{3}$. Vagyis: $c_1=\frac{161}{3}$. A két egyenes metszéspontja: $C\left(\frac{161}{3};\frac{221}{3}\right)$. $b)$ Az $AC$ egyenes egyenlete könnyen felírható, hiszen a meredeksége 1, az $y$ tengelyt pedig a $D\left(0;20\right)$ pontban metszi: $y=x+20$. A $BC$ egyenes egyenlete is felírható, mert ismerjük két pontjának koordinátáit. Használjuk a két ponton áthaladó egyenes egyenletét: $\begin{array}{c}{\displaystyle \left(y-y_1\right)\left(x_2-x_1\right)=\left(x-x_1\right)\left(y_2-y_1\right)\mathrm{.}}\end{array}$ Írjuk be az ismert pontok koordinátáit: $\begin{array}{c}{\displaystyle y\cdot \left(\frac{161}{3}-40\right)=\left(x-40\right)\cdot \frac{221}{3}\mathrm{,}221x-41y=8840.}\end{array}$ Tehát az egyenesek egyenlete: $y=x+20$ és $221x-41y=8840$.   7. Két számot választunk véletlenszerűen a $\left[0;1\right]$ számközben. Mi a valószínűsége annak, hogy összegük $1$-nél, szorzatuk pedig $\frac{4}{25}$-nél kisebb lesz?  (16 pont)   Megoldás. Jelöljük a vizsgált eseményt $A$-val. A két véletlenszerűen választott $x$ és $y$ számnak a sík egységnégyzetének $\left(x;y\right)$ koordinátájú pontját feleltetjük meg. Az $A$ esemény fennáll, ha az $\begin{array}{c}{\displaystyle x+y<1\text{és}xy<\frac{4}{25}}\end{array}$ egyenlőtlenségek egyidejűleg teljesülnek. Az ezeknek az egyenlőtlenségeknek eleget tevő pontok az egységnégyzet satírozott részére esnek. Ennek a résznek a területét kell kiszámítanunk.     Meghatározzuk az $x+y=1$ egyenes és az $xy=\frac{4}{25}$ hiperbola metszéspontjait. Az $y=1-x$ helyettesítéssel kapjuk: $\begin{array}{c}{\displaystyle x\left(1-x\right)=\frac{4}{25}\mathrm{,}{x}^2-x+\frac{4}{25}=0.}\end{array}$ A másodfokú egyenlet megoldásai: $x_1=0\mathrm{,}8$, $x_2=0\mathrm{,}2$. A megfelelő ordinátákat visszahelyettesítéssel kapjuk: $y_1=0\mathrm{,}2$, $y_2=0\mathrm{,}8$. A bevonalkázott részben a $\left[0;0\mathrm{,}2\right]$ és a $\left[0\mathrm{,}8;1\right]$ intervallumok fölötti részek együttesen 0,2 nagyságú területet adnak. A $\left[0\mathrm{,}2;0\mathrm{,}8\right]$ intervallumon az $y=0\mathrm{,}16\cdot \frac{1}{x}$ hiperbola alatti rész területét kell kiszámítani: $\begin{array}{c}{\displaystyle 0\mathrm{,}16\cdot \underset{0\mathrm{,}2}{\overset{0\mathrm{,}8}{\int }}\frac{1}{x}dx=0\mathrm{,}16\cdot {\left[\text{ln}|x|\right]}_{0\mathrm{,}2}^{0\mathrm{,}8}=0\mathrm{,}16\cdot \left(\text{ln}\mathrm{0,8}-\text{ln}\mathrm{0,2}\right)=\mathrm{0,16}\cdot \text{ln}4.}\end{array}$ Az $A$ esemény szempontjából kedvező rész területe: $t=0\mathrm{,}2+0\mathrm{,}16\cdot \text{ln}4$. Az egységnégyzet területe: $T=1$, így az $A$ esemény valószínűsége: $\begin{array}{c}{\displaystyle P\left(A\right)=\frac{t}{T}=0\mathrm{,}2+0\mathrm{,}16\cdot \text{ln}4\approx 0\mathrm{,}42.}\end{array}$ Tehát kb. 0,42 a valószínűsége annak, hogy a véletlenszerűen választott számok eleget tesznek a feltételeknek.   8. Egy forgáskúp és egy henger alaplapja közös. A kúp csúcsa a henger fedőlapjának középpontja. Határozzuk meg a kúp tengelyének és alkotójának hajlásszögét, ha a henger és a kúp felszínének aránya $7:4$.  (16 pont)     Megoldás. Készítsük el a kúp tengelymetszetéről a vázlatrajzot. Az ábra jelölései és a felszínekre vonatkozó összefüggések alapján: $\begin{array}{c}{\displaystyle \frac{A_{\text{henger}}}{A_{\text{kúp}}}=\frac{2r^2\pi +2r\pi m}{r^2\pi +r\pi a}=\frac{7}{4}\mathrm{.}}\end{array}$ Egyszerűsítés után kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{2\left(r+m\right)}{r+a}=\frac{7}{4}\mathrm{,}\text{amiből}\frac{1+\frac{m}{r}}{1+\frac{a}{r}}=\frac{7}{8}\mathrm{.}}\end{array}$ Tudjuk, hogy $\text{ctg}\alpha =\frac{m}{r}$ és $\frac{1}{\text{sin}\alpha }=\frac{a}{r}$. Ezeket behelyettesítve és felhasználva, hogy $\text{ctg}\alpha =\frac{\text{cos}\alpha }{\text{sin}\alpha }$, a következőt kapjuk: $\begin{array}{c}{\displaystyle \frac{1+\frac{\text{cos}\alpha }{\text{sin}\alpha }}{1+\frac{1}{\text{sin}\alpha }}=\frac{7}{8}\mathrm{.}}\end{array}$ Rendezve az egyenletet: $\begin{array}{c}{\displaystyle \text{sin}\alpha +8\text{cos}\alpha =\mathrm{7,}}\end{array}$ $\begin{array}{c}{\displaystyle \frac{1}{\sqrt[]{1^2+8^2}}\text{sin}\alpha +\frac{8}{\sqrt[]{1^2+8^2}}\text{cos}\alpha =\frac{7}{\sqrt[]{1^2+8^2}}\mathrm{,}}\end{array}$ amit közelítő értékekkel így írhatunk: $\begin{array}{c}{\displaystyle \text{sin}\alpha \text{cos}82\mathrm{,}{87}^{\circ }+\text{cos}\alpha \text{sin}82\mathrm{,}{87}^{\circ }=0\mathrm{,}8682.}\end{array}$ Alkalmazzuk a $\text{sin}\left(\alpha +\beta \right)$-ra vonatkozó addíciós tételt: $\begin{array}{c}{\displaystyle \text{sin}\left(82\mathrm{,}{87}^{\circ }+\alpha \right)=\text{sin}60\mathrm{,}{25}^{\circ }\mathrm{.}}\end{array}$ Ennek a trigonometrikus egyenletnek a megoldása: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\alpha }_1}& {\displaystyle =-22\mathrm{,}{62}^{\circ }+k_1\cdot {360}^{\circ }\mathrm{,}\text{ahol}{k}_1\in \text{Z};}\hfill \\ \hfill {\displaystyle {\alpha }_2}& {\displaystyle =36\mathrm{,}{88}^{\circ }+k_2\cdot {360}^{\circ }\mathrm{,}\text{ahol}{k}_2\in \text{Z}\mathrm{.}}\hfill \end{array}}$ Innen a feladat egyedüli megoldása: $\alpha =36\mathrm{,}{88}^{\circ }$. Vagyis a kúp alkotójának és magasságának hajlásszöge: $36\mathrm{,}{88}^{\circ }$.   9. 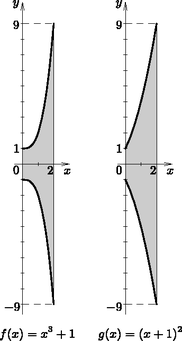A $\left[0;2\right]$ intervallumon értelmezett $f\left(x\right)=x^3+1$ és $g\left(x\right)={\left(x+1\right)}^2$ függvények grafikonját megforgatjuk az $x$ tengely körül. $a)$ Számítsuk ki az így kapott forgástestek alap- és fedőlapjának területét. $b)$ Számítsuk ki a két test térfogatát.  (16 pont)   Megoldás. Lerajzoljuk a függvények grafikonját, és a megforgatás után kapott testek síkmetszetét.     $a)$ A két test alap és fedőlapja is azonos méretű, hiszen $f\left(0\right)=g\left(0\right)=1$, $f\left(2\right)=g\left(2\right)=9$. Vagyis az alaplapok sugara 1, a fedőlapok sugara 9. Az alaplap területe: $t=\pi$, a fedőlap területe: $T=81\pi$. $b)$ Használjuk a $\begin{array}{c}{\displaystyle V=\pi \underset{a}{\overset{b}{\int }}{\left[f\left(x\right)\right]}^{2}dx}\end{array}$ térfogatképletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V_1}& {\displaystyle =\pi \underset{0}{\overset{2}{\int }}{\left(x^3+1\right)}^{2}dx=\pi \underset{0}{\overset{2}{\int }}\left(x^6+2x^3+1\right)dx=\pi {\left[\frac{x^7}{7}+2\cdot \frac{x^4}{4}+x\right]}_0^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\pi \left(\frac{2^7}{7}+2\cdot \frac{2^4}{4}+2\right)\approx 88\mathrm{,}86.}\hfill \\ \hfill {\displaystyle V_2}& {\displaystyle =\pi \underset{0}{\overset{2}{\int }}{\left(x+1\right)}^{4}dx=\pi \underset{0}{\overset{2}{\int }}\left(x^4+4x^3+6x^2+4x+1\right)dx=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\pi {\left[\frac{x^5}{5}+4\cdot \frac{x^4}{4}+6\cdot \frac{x^3}{3}+4\cdot \frac{x^2}{2}+x\right]}_0^2=\pi {\left[\frac{2^5}{5}+4\cdot \frac{2^4}{4}+6\cdot \frac{2^3}{3}+4\cdot \frac{2^2}{2}+2\right]}_0^2\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx 152\mathrm{,}05.}\hfill \end{array}}$