Cím: Egy kártyatrükk és ami mögötte van
Szerző(k):  Csajbók Bence 
Füzet: 2010/május, 258 - 263. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy bűvész 13 db, egyenként 4-4 kártyából álló kupacba osztotta az 52 lapos francia kártya lapjait, majd a kupacokat az 1. ábrán látható módon hátlappal felfelé, egy olyan kör alakú asztalra helyezte, amely a középpontja körül bármerre elforgatható.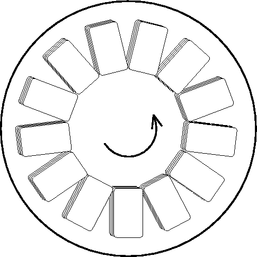

 
 

1. ábra
 

A mutatvány a következő: a bűvész kihív egy önként jelentkezőt a nézők közül és felkéri, hogy forgassa meg párszor az asztalt, majd válasszon ki két tetszőleges kupacot. Az így kiválasztott 8 lapot nézze meg és amennyiben talál köztük azonos értékű kártyákat, úgy azokat hátlappal felfelé tegye félre, a többi lapot pedig helyezze vissza oda, ahonnan elvette (a kártyák ügyes elrendezése miatt minden esetben két kártyát kell félretennie).
Ezután a bűvész választ két kupacot. Ezeket megnézi, majd két lap kivételével visszateszi a kártyákat a helyükre. Végül megkéri az önként jelentkezőt, vegye kézbe ő is félretett lapjait és mutassák meg a közönségnek egyszerre, mi is az a 2-2 kártya, ami a kezükben van.
Meglepetésre, mind a négy kártyának ugyanaz az értéke.
 

A megfejtéshez először gondoljuk végig: hogyan lehetséges, hogy a jelentkezőnek minden esetben pontosan két kártyát kell félretennie. Hogy ez így legyen, semelyik két kupacban nem szerepelhet ugyanaz az érték kettőnél többször, vagyis minden kupacban minden kártya legfeljebb egyszer szerepelhet. Ebből már adódik első tulajdonságunk:
 
1. Bármely két különböző kupacot választva kell lennie pontosan egy olyan értéknek, amely mindkét kupacban szerepel.
 

Mivel egy kupacon belül csak különböző értékű lapok szerepelnek, ezért minden kupacon belül (42) különböző értékekből álló értékpár van. Egyik ilyen pár sem szerepelhet két különböző kupacban, hiszen ha lenne két ilyen kupac, ezekre nem teljesülne az 1. tulajdonság. Tehát azon különböző értékekből álló értékpárok száma, ahol a pár mindkét tagja ugyanabban a kupacban szerepel: 13⋅(42)=(132). Ez megegyezik az összes különböző értékekből álló értékpárok számával, tehát az alábbi tulajdonságnak is teljesülnie kell:
 
2. Bármely két különböző értéket választva kell lennie pontosan egy olyan kupacnak, melyben mindkét érték szerepel.
 

A trükk vizsgálatát egy kicsit félretéve, ismerkedjünk meg a projektív síkokkal. Legyen P egy tetszőleges halmaz, E pedig P bizonyos részhalmazainak halmaza. P elemeit pontoknak, E elemeit pedig egyeneseknek fogjuk hívni. Amennyiben egy P∈P pont és e∈E egyenes esetén P∈e teljesül, akkor azt mondjuk, hogy a P pont illeszkedik az e egyenesre. A Π=(P,E) párt projektív síknak nevezzük, ha az alábbi négy axiómának eleget tesz:
P1.bármely két különböző ponthoz pontosan egy olyan egyenes van, melyre mindkét pont illeszkedik,
P2.bármely két különböző egyeneshez pontosan egy olyan pont van, mely mindkét egyenesre illeszkedik,
P3.minden egyenesre illeszkedik legalább három különböző pont,
P4.minden pont legalább három különböző egyenesre illeszkedik.

A P1, P2 axiómák helyett a geometriai szóhasználattal élve azt is mondhatjuk, hogy két ponton át egyértelműen létezik az őket összekötő egyenes, illetve, hogy bármely két egyenesnek egyértelműen létezik metszéspontja. A P3, P4 axiómák az elfajuló esetek kizárására szolgálnak.
Szembetűnő a hasonlóság az első két axióma és a kártyakupacokra vonatkozó két tulajdonság között. Legyen P a 13 db kupacból álló halmaz. Definiáljuk továbbá a kupacok alábbi részhalmazait:

hA:azoknak a kupacoknak a halmaza, melyekben szerepel ász;
h2:azoknak a kupacoknak a halmaza, melyekben szerepel 2-es;
⋯
hK:azoknak a kupacoknak a halmaza, melyekben szerepel király.

Mivel a francia kártyában 13 különböző értékű lap van és mindegyik kupacban minden érték legfeljebb egyszer szerepelhet, ezért összesen 13 db 4-elemű részhalmazt definiáltunk a kupacokon. Legyen E={hA,h2,⋯,hK}, ekkor a (P,E)-pár az 1. és 2. tulajdonság miatt kielégíti a P1, P2 axiómákat, és nyilvánvalóan kielégíti P3-at és P4-et is, tehát projektív síkot alkot. Az alábbi tétel bizonyítását feladatnak hagyjuk (megtalálható például [1]-ben vagy az interneten is elérhető [2]-ben):
 
Tétel. Ha a Π projektív síknak van olyan egyenese, melyre n+1 pont illeszkedik, akkor Π minden egyenesére n+1 pont illeszkedik, Π minden pontján át n+1 egyenes megy át, Π összesen n2+n+1 pontot és ugyanennyi egyenest tartalmaz.
 

Az előző tétel alapján értelmes a következő definíció:
 
Definíció. A Π projektív sík rendje n, ha Π-nek létezik olyan egyenese, melyre n+1 pont illeszkedik. Ez esetben Π-t n-rendű véges projektív síknak nevezzük.
 

Hogy milyen n értékek esetén létezik n-rendű projektív sík, illetve adott n esetén hány db egymástól lényegesen különböző (nem izomorf) sík létezik, máig megoldatlan probléma. Ha n prímhatvány, akkor véges testek segítségével tudunk n-rendű síkot konstruálni (ez szintén megtalálható [1]-ben), és a sejtés az, hogy csak prímhatvány rendű síkok léteznek.
Annyit azonban már mi is beláttunk, hogy ha hihetünk a bűvészünknek és tényleg kupacokba tudja osztani az 1. és 2. tulajdonságoknak megfelelően az 52-lapos francia kártyát, akkor létezik 3-rendű projektív sík, hiszen a fent említett módon definiált (P,E) pár kielégíti az axiómákat és 32+3+1=13.
A továbbiakban ismertetünk egy módszert, aminek a segítségével véges projektív síkokat készíthetünk. Továbbá megmutatjuk, hogyan kell a bűvésznek szétosztani a kártyákat, illetve honnan tudja, hogy melyik két kupacot kell választania.
 
A ciklikus modell
 

Legyen S az O középpontú körbe írt szabályos (n2+n+1)-szög. Ha P és Q a sokszög két különböző csúcsa, akkor nevezzük a P és Q távolságának k-t, ha a rövidebb PQ ívhez tartozó középponti szög k⋅360∘/(n2+n+1). Legfeljebb hány csúcsát lehet kiválasztani S-nek, hogy bármely kettő távolsága különböző legyen? Mivel a sokszög csúcsai összesen
n2+n2=(n+12)
különböző távolságot határoznak meg, ezért legfeljebb (n+1)-et. Tegyük fel, hogy sikerült kiválasztanunk (n+1) db csúcsot a megadott feltétellel és az általuk meghatározott részsokszöget jelöljük R-rel (az ilyen részsokszögeket szokás teljesen szabálytalan részsokszögnek nevezni). A 2. ábrán az n=3 esetben berajzoltunk egy teljesen szabálytalan résznégyszöget.
 
 

2. ábra
 

R-nek O-körüli k⋅360∘/(n2+n+1) szögű elforgatottjait (k=0,1,...,n2+n) jelöljük R0,R1,...,Rn2+n-vel. Az Ri részsokszög csúcsainak a halmazát pedig ri-vel.
A pontok, vagyis P legyen S csúcsainak a halmaza, az egyenesek pedig E={r0,r1,...,rn2+n}. Tehát a P∈P pont pontosan akkor illeszkedik az rj∈E egyenesre, ha P az R részsokszög j⋅360∘/(n2+n+1) szögű elforgatottjának az egyik csúcsa.
Megmutatjuk, hogy modellünk kielégíti a P1‐P4 axiómákat. Legyen P,Q két különböző pont, melyek távolsága k. R csúcsai között minden távolság pontosan egyszer fordul elő, így pontosan egy olyan elforgatottja van, melynek P és Q is csúcsa. Ezzel beláttuk, hogy P1 teljesül.
Legyen Rm és Rl két különböző egyenes, ekkor n2+n+1=n(n+1)+1 páratlan volta miatt, az Rm-et Rl-be, illetve az Rl-t Rm-be vivő pozitív irányú forgatások közül az egyiknek a szöge kisebb mint 180∘. Az indexeket választhatjuk úgy, hogy ez az Rm-et Rl-be vivő forgatás legyen és a szögét jelöljük k⋅360∘/(n2+n+1)-val. Ekkor
k∈{1,...,n2+n2}.
Egy M pont pontosan akkor van rajta mindkét szóbanforgó egyenesen, ha Rm-nek létezik egy olyan N csúcsa, melyre az NOM irányított szög +k⋅360∘/(n2+n+1). Ilyen M,N pontpár viszont pontosan egy van Rm csúcsai között, hiszen ott R csúcsaihoz hasonlóan minden távolság pontosan egyszer lép fel.
Ezzel P2 teljesülését is beláttuk, P3 és P4 teljesülése pedig n≥2 esetén nyilvánvaló.
Az így kapott véges projektív síkokat szokás ciklikus síkoknak nevezni. Mivel a 2. ábrán látható szabályos 13-szögben a berajzolt (1,3,4,8-csúcsok által meghatározott) résznégyszög teljesen szabálytalan, ezért létezik 3-rendű ciklikus sík. Megmutatható, hogy lényegében ez az egyetlen 3-rendű projektív sík, vagyis bármely más, a P1‐P4 axiómákat teljesítő 13 pontból álló modell pontjai és egyenesei, illeszkedéstartó módon megfeleltethetők a mi példánk pontjainak és egyeneseinek. Ez azonban nincs mindig így, például 9-rendű projektív síkból négy különböző létezik, melyek közül csak az egyiket kapjuk meg a fent ismertetett eljárással.
Bizonyítható, hogy ha n prímhatvány, akkor a szabályos (n2+n+1)-szög csúcsai közül mindig kiválasztható egy teljesen szabálytalan (n+1)-szög (lásd [1]), és az így kapott ciklikus sík lényegében ugyanaz, mint a korábban említett (de nem részletezett) véges testek segítségével konstruálható sík. A legkisebb szám, mely esetén ez nem tehető meg, n=6. Ezt az állítást úgy is megfogalmazhatjuk, hogy egy szabályos 62+6+1=43-szög bármely 7 csúcsa által meghatározott 21 távolság között lesz két egyforma.
Végezetül rátérünk a trükk magyarázatára.
A kártyákat a trükk megkezdése előtt a 3. ábrán látható módon úgy osztjuk szét a 13 kupacba, hogy bármely 4 azonos értékű kártya a 2., illetve 3. ábrán berajzolt teljesen szabálytalan négyszög egy elforgatottjának a csúcsait adja. Például az 1., 3., 4., 8. kupacokba kerüljenek az ászok, a 2., 4., 5., 9. kupacokba a 2-esek, ..., végül a 13., 2., 3., 7. kupacokba a királyok.
 
 

3. ábra
 

Ekkor az az állítás, hogy a 3. kupacban szerepel ász, úgy is megfogalmazható, hogy a 3. kupacnak megfelelő pont rajta van az ászok által meghatározott egyenesen. Tulajdonképpen minden kártyalap megfeleltethető a 3-rendű ciklikus síkon egy pont-egyenes illeszkedés párnak. Ezek száma valóban 52, hiszen a síkon 13 pont van, melyek mindegyike pontosan 4 különböző egyenesre illeszkedik.
Amikor a néző kiválaszt két kupacot, az egyértelműen meghatározza a négyszög egyik elforgatottját. A bűvésznek csak oda kell képzelnie a négyszög másik két csúcsát és az ott található két kupacot kell választania. Mivel az így kiválasztott 2-2 kupac egy egyenesre esik, ezért mindkét kupacpárban ugyanaz az érték fog megegyezni. A bűvésznek ki kell választania saját kupacaiból a két egyforma kártyát és ezeket kell a kezében tartania. Mivel csak a kártyák egymáshoz viszonyított helyzete számít, ezért az asztal elforgatása semmiben sem befolyásolja a mutatványt.
A táblázat azt mutatja, hogy a fenti módszerrel mely kártyák kerülnek az egyes kupacokba. Természetesen sok más elrendezés is lehetséges, nem számít ugyanis, hogy az egyes értékeket a négyszög mely elforgatottjához rendeljük. A táblázat k. oszlopában a k. kupacban szereplő lapok szerepelnek, a színek feltüntetése nélkül.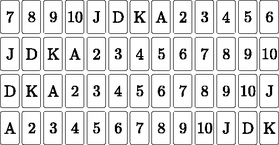
 
 

Az érdeklődő olvasók számára ajánlunk néhány feladatot:
 
1. Keressünk teljesen szabálytalan
(a) 3-szöget, a szabályos 7-szögben,
(b) 5-szöget, a szabályos 21-szögben.
(c) Hány db forgatással egymásba nem vihető teljesen szabálytalan 4-szög választható ki a szabályos 13-szög csúcsai közül?
 
2. Ha a kártyák egy kupacon belüli sorrendjét nem vesszük figyelembe és az egymásból forgatással megkapható elrendezéseket nem tekintjük különbözőnek, akkor hány különböző kártya-elrendezésben adható elő a trükk?
 
3. Előadható-e a trükk olyan kártya-elrendezés mellett, ahol minden kupacban négy különböző színű kártya szerepel?
 
4. Mutassuk meg, hogy a néző és a bűvész által kiválasztott 4 kupacban minden érték szerepel.
 
5. A trükk úgy is elvégezhető, hogy a bűvész nem két kupacot, hanem egyből 2 kártyát választ, melyek értéke megegyezik a néző által félretett lapok értékével. Hogyan lehetséges ez?
 
Irodalomjegyzék
 

[1]Kiss György és Szőnyi Tamás: Véges Geometriák, Polygon Kiadó, Szeged (2001).
[2]Bérczi Gergely, Gács András és Szőnyi Tamás: Véges projektív síkok, Új matematikai mozaik (szerk.: Hraskó András), Budapest, Typotex Kiadó (2002). http://www.tankonyvtar.hu/konyvek/uj-matematikai-mozaik/uj-matematikai-mozaik-081030-26