Kezdőlap


Cím:	Latin négyzetek, szép sudoku megoldások és véges geometriák II.
Szerző(k):	Kiss György
Füzet:	2010/április, 194 - 200. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

^{$^{*}$}

3. Szép sudoku megoldások

Célunk, hogy

N

geometriai tulajdonságait felhasználva leírjuk a szép sudoku megoldásokat.

Definíció. Az

x = (x_{1}, x_{2}, x_{3}, x_{4})

és

y = (y_{1}, y_{2}, y_{3}, y_{4})

N

-beli elemek Hamming-távolsága,

d (x,y)

azon

i \in {1,2,3,4}

indexek száma, melyekre

x_{i} \neq y_{i}

teljesül.

Az így mért eltérést azért nevezik távolságnak, mert rendelkezik a geometriából ismert ,,szokásos'' távolság legfontosabb tulajdonságaival. Például igaz a háromszög-egyenlőtlenség, azaz tetszőleges

x

y

z

vektorok Hamming-távolságára

\begin{matrix} d (x,y) + d (y,z) \geq d (x,z) . \end{matrix}

A Hamming-távolságot persze nemcsak 4 hosszú vektorok esetén lehet értelmezni. Erről részletesen olvashatunk a lapunk 2007. májusi számában megjelent [2] cikkben, vagy a [3] könyv 13. fejezetében.

Tétel. Szép megoldás esetén bármely két ugyanazon számjegyet tartalmazó mezőhöz tartozó vektor Hamming-távolsága pontosan

3

Bizonyítás. Először azt mutatjuk meg, hogy két ilyen mező távolsága legalább 3. Tegyük fel, hogy két mezőben ugyanaz a számjegy áll, a mezők távolsága pedig legfeljebb 2. Ez azt jelenti, hogy a két mezőhöz tartozó vektoroknak van két azonos koordinátájuk. Ez a két koordináta hat különböző párban fordulhat elő. Bármelyik párt is adjuk meg, az egyértelműen meghatároz egy sort (

x_{1}

és

x_{2}

), vagy oszlopot (

x_{3}

és

x_{4}

), vagy törött sort (

x_{2}

és

x_{3}

), vagy törött oszlopot (

x_{1}

és

x_{4}

), vagy kis négyzetet (

x_{1}

és

x_{3}

), vagy pozíciót (

x_{2}

és

x_{4}

). Vagyis az egyezés ellentmond a szép megoldás definíciójának.
Nézzünk most 9 olyan mezőt, melyekben ugyanaz a számjegy áll. A mezőknek megfelelő 9 vektorból

9 \times 8 = 72

rendezett pár készíthető. Ezek páronkénti távolságainak összege az előzőek szerint legalább

72 \times 3 = 216

.
Ez a távolságösszeg az egyes koordinátákban fellépő eltérések összegéből adódik. Vizsgáljuk meg a vektorok első koordinátáit. Legyen az első koordináták közt

e_{0}

darab 0,

e_{1}

darab 1 és

e_{2}

darab 2. Ekkor

e_{0} + e_{1} + e_{2} = 9

, továbbá az első koordináták hozzájárulása a távolságösszeghez:

\begin{matrix} e_{0} (e_{1} + e_{2}) + e_{1} (e_{0} + e_{2}) + e_{2} (e_{0} + e_{1}) = e_{0} (9 - e_{0}) + e_{1} (9 - e_{1}) + e_{2} (9 - e_{2}) = \\ = 9 \cdot (e_{0} + e_{1} + e_{2}) - (e_{0}^{2} + e_{1}^{2} + e_{2}^{2}) = 81 - (e_{0}^{2} + e_{1}^{2} + e_{2}^{2}) . \end{matrix}

Viszont a számtani és a négyzetes közép közti egyenlőtlenség szerint

\begin{matrix} \sqrt[]{\frac{e_{0}^{2} + e_{1}^{2} + e_{2}^{2}}{3}} \geq \frac{e_{0} + e_{1} + e_{2}}{3} = 3, \end{matrix}

(1)

azaz

\begin{matrix} e_{0}^{2} + e_{1}^{2} + e_{2}^{2} \geq 27. \end{matrix}

Tehát az első koordináták eltéréseinek összege legfeljebb

81 - 27 = 54

. Ugyanezeket az egyenlőtlenségeket nyilván felírhatjuk a második, harmadik és negyedik koordinátákra is. Vagyis a távolságok összege legfeljebb

4 \times 54 = 216

.
Ez csak úgy lehet, ha a távolságösszeg pontosan 216, azaz bármely két vektor távolsága éppen 3.

□

Nevezzük jó halmaznak az

N

olyan 9 elemű részhalmazait, melyekben bármely két elem Hamming-távolsága pontosan 3.

Következmény. Bármely jó halmaz

9

vektora közt minden

i = 1,2,3,4

és

j = 0,1,2

esetén pontosan

3

olyan van, melynek az

i

-edik koordinátája

j

Bizonyítás. Jó halmaz esetén az előző tétel bizonyításában szereplő (1) egyenlőtlenségben egyenlőség áll, ezért

e_{0} = e_{1} = e_{2} = 3

. Továbbá, az ennek megfelelő, a többi koordinátára vonatkozó egyenlőtlenségekben is egyenlőségnek kell teljesülnie, vagyis a 9 vektor minden koordinátájában 3-3 darab 0, 1 és 2 fordul elő.

□

Feladat. Mutassuk meg, hogy legfeljebb

9

N

-beli vektor adható meg úgy, hogy közülük bármely kettő Hamming-távolsága legalább

3

A továbbiakban célunk a jó halmazok leírása.

Tétel.

C

pontosan akkor jó halmaz, ha bármely

x

-re

C + x

is jó halmaz.

Bizonyítás. Bármely

x

y

z

vektorok esetén

\begin{matrix} d (y, z) = d (y + x, z + x) \end{matrix}

amiből azonnal adódik az állítás.

□

Tételünkből következik, hogy minden jó halmaznak van olyan eltoltja, amely tartalmazza a

0

vektort. Tehát a továbbiakban elegendő az ilyen tulajdonságú jó halmazokat vizsgálnunk.

Tétel. Ha egy jó halmazban benne vannak az egymástól különböző

x

és

y

vektorok, akkor a

2 (x + y)

vektor is benne van.

Bizonyítás. Mivel modulo 3 számolunk, azért

\begin{matrix} x + y + 2 (x + y) = 0 . \end{matrix}

Tudjuk, hogy

d (x, y) = 3

. Tehát

x

és

y

pontosan egy koordinátában egyezik meg. Feltehetjük, hogy

x_{1} = y_{1} = a

. A jó halmazban még pontosan egy olyan

z

vektor van, melyre

z_{1} = a

teljesül. Mivel

d (x, z) = d (y, z) = 3

, azért

i = 2,3,4

esetén az

x

y

és

z

vektorok

i

-edik koordinátái páronként különbözőek, azaz

{x_{i}, y_{i}, z_{i}} = {0,1,2}

. Ezért

x_{i} + y_{i} + z_{i} = 0 + 1 + 2 = 0

. S mivel

x_{1} + y_{1} + z_{1} = a + a + a = 0

, azért

x + y + z = 0

, tehát

\begin{matrix} z = - (x + y) = 2 (x + y) . □ \end{matrix}

Tétel. Ha a

C

jó halmazban benne van

0

, valamint a lineárisan független

a

és

b

vektorok, akkor

C

egy sík, pontosabban

\begin{matrix} C = S_{a, b, 0} . \end{matrix}

Bizonyítás. Az előző tételt

x = a

és

y = b

x = 0

és

y = a

valamint

x = 0

és

y = b

esetén alkalmazva kapjuk, hogy

C

tartalmazza a

2 (a + b)

2 a

és

2 b

vektorokat. Mivel

a

és

b

lineárisan függetlenek, ezért

a \neq 2 b \neq 2 a \neq b

. Tehát az előző tételt alkalmazhatjuk

x = a

és

y = 2 b

x = b

és

y = 2 a

valamint

x = 2 a

és

y = 2 b

választással is. Ezekből kapjuk, hogy

C

tartalmazza a

2 (a + 2 b) = 2 a + b

, a

2 (b + 2 a) = 2 b + a

és a

2 (2 a + 2 b) = a + b

vektorokat is.

□

Ezek után már meg tudjuk adni az összes jó halmazt.

Tétel. Legyenek

a

és

b

lineárisan független vektorok. Ha teljesül, hogy

d (0, a) = d (0, b) = d (a, b) = 3

, akkor

S_{a, b, 0}

jó halmaz.

Bizonyítás. Azt kell megmutatnunk, hogy

S_{a, b, 0}

bármely két különböző elemének Hamming-távolsága pontosan 3. Mivel

d (x, y) = d (x - y, 0)

, azért elég azt megmutatnunk, hogy

S_{a, b, 0}

minden

0

-tól különböző elemének pontosan 3 nemnulla koordinátája van.
Legyen

a = (a_{1}, a_{2}, a_{3}, a_{4})

és

b = (b_{1}, b_{2}, b_{3}, b_{4})

. Mivel

d (0, a) = d (0, b) = 3

, ezért

a

-nak is és

b

-nek is pontosan egy koordinátája

0

. Feltehetjük, hogy

a_{1} = 0

. Ekkor

b_{1} \neq 0

, mert ha

b_{1} = 0

lenne, akkor

d (a, b) = 3

miatt

i = 2,3,4

esetén

a_{i} \neq b_{i}

lenne, s mivel ezen koordináták egyike sem 0, azért

{a_{i}, b_{i}} = {1,2}

is teljesülne. Ekkor viszont

a + b = 0

, azaz

b = 2 a

lenne, ami ellentmond a feltételeinknek.
Tehát

b_{1} \neq 0

. Feltehetjük, hogy

b

egyetlen 0 koordinátája

b_{2}

. Mivel

d (a, b) = 3

és

a_{1} \neq b_{1}

valamint

a_{2} \neq b_{2}

, azért az

(a_{3}, b_{3})

és

(a_{4}, b_{4})

párok közül az egyik két egyező, a másik pedig két különböző koordinátából áll. Továbbá tudjuk, hogy ezen koordináták egyike sem 0. Ezért feltehető, hogy

a_{3} = b_{3}

és

{a_{4}, b_{4}} = {1,2}

, azaz

b_{4} = 2 a_{4}

. Ekkor minden

c \in S_{a, b, 0}

esetén

\begin{matrix} c & = α a + β b = (α a_{1} + β b_{1}, α a_{2} + β b_{2}, α a_{3} + β b_{3}, α a_{4} + β b_{4}) = \\ = (β b_{1}, α a_{2}, (α + β) a_{3}, (α + 2 β) a_{4}) . \end{matrix}

Megmutatjuk, hogy

c

-nek pontosan egy koordinátája 0. Ha

α = 0

, akkor

β \neq 0

. Tehát ekkor csak

c_{2} = 0

. Ugyanígy kapjuk, hogy

β = 0

esetén csak

c_{1} = 0

. Ha

α \neq 0

és

β \neq 0

, akkor

c_{1} \neq 0

és

c_{2} \neq 0

nyilván teljesül. Ha továbbá

α = β

, akkor

\begin{matrix} c_{3} = (α + β) a_{3} = 2 α a_{3} \neq 0, \end{matrix}

mert

a_{3} \neq 0

. Viszont

c_{4} = (α + 2 β) a_{4} = 3 α a_{4} = 0

. Ha pedig

α \neq β

, akkor

β = 2 α

, tehát

c_{3} = (α + β) a_{3} = 3 α a_{3} = 0

, viszont

c_{4} = (α + 2 β) a_{4} = α a_{4} \neq 0

□

Következmény. A

0

vektort tartalmazó jó halmazok pontosan azok az

S_{a, b, 0}

síkok, melyekre teljesül, hogy

d (0, a) = d (0, b) = d (a, b) = 3

Tétel. A

0

vektort tartalmazó jó halmazok száma

8

Bizonyítás. A jó halmaz pontosan 3 olyan vektort tartalmaz, melyek első koordinátája 0, ezek egyike a

0

. A másik két ilyen vektor második koordinátái 0-tól is és egymástól is különböznek, ezért egyikük második koordinátája 1. Legyen ez a vektor

a

. Ugyanígy kapjuk, hogy van a halmazban egy olyan

b

vektor, melyre

b_{1} = 1

és

b_{2} = 0

. Tehát

\begin{matrix} a = (0,1, a_{3}, a_{4}) és b = (1,0, b_{3}, b_{4}), \end{matrix}

ahol

d (a, b) = 3

és

a_{1} \neq b_{1}

valamint

a_{2} \neq b_{2}

miatt az

(a_{3}, b_{3})

és

(a_{4}, b_{4})

párok közül az egyik két egyező, a másik pedig két különböző, nemnulla koordinátából áll. Ezért az

(a_{3}, a_{4})

párt

2 \cdot 2 = 4

-féleképp választhatjuk. Ezután

b_{3}

-at 2-féleképp választhatjuk, s ez már

b_{4}

-et is meghatározza.

□

Feladatok. Mutassuk meg, hogy a

0

vektort tartalmazó

8

jó halmaz közül bármelyiket is választjuk ki, a maradék

7

halmaz közt pontosan

4

olyan van, amelyik az elsőnek választott halmazunkat egyenesben metszi.
Mutassuk meg, hogy a

0

vektort tartalmazó

8

jó halmaz közül nem lehet kiválasztani

3

halmazt úgy, hogy közülük bármelyik

2

metszete egyenes legyen.

Bármely szép sudoku megoldás esetén az azonos számjegyet tartalmazó mezőknek megfelelő vektorok egy-egy jó halmazt alkotnak. Tehát a szép megoldás nem más, mint az

N

négydimenziós tér 81 vektorának beosztása 9 darab páronként diszjunkt jó halmazba. Jelölje

i = 1,2, ...,9

esetén

S_{i}

azt a jó halmazt, amelyet az

i

számjegyet tartalmazó mezőknek megfelelő vektorok alkotnak. Láttuk, hogy

S_{i}

minden

i

-re egy-egy sík. Jelölje

S_{i}'

S_{i}

-nek azt az eltoltját, amely tartalmazza a

0

vektort.
A legegyszerűbben úgy kapunk szép megoldást, ha mindegyik

S_{i}

halmaz ugyanannak a jó halmaznak az eltoltja, azaz az

S_{i}'

halmazok megegyeznek. Először vizsgáljuk meg, hogy két eltolt mikor metszi egymást.

Tétel. Legyen

C

0

vektort tartalmazó jó halmaz. Ekkor a

C + x

és

C + y

jó halmazok

x - y \in C

esetén egybeesnek,

x - y \notin C

esetén pedig nincs közös elemük.

Bizonyítás. Azt kell megmutatnunk, hogy ha a két halmaznak van közös eleme, akkor

x - y \in C

és a két halmaz megegyezik. Tegyük fel, hogy

\begin{matrix} z \in (C + x) \cap (C + y) . \end{matrix}

Ekkor vannak olyan

C

-beli

c_{1}

c_{2}

vektorok, melyekre

z = x + c_{1} = y + c_{2}

, azaz

x - y = c_{2} - c_{1} = c_{2} + 2 c_{1}

. Vagyis

x - y

C

-beli vektor. Mivel

C

sík, azért ebből következik, hogy

C + (x - y) = C

, tehát

\begin{matrix} C + y = (C + (x - y)) + y = C + (x - y + y) = C + x, \end{matrix}

ami épp a bizonyítandó állítás.

□

Adott

C

, a

0

-t tartalmazó jó halmaz esetén az a 9 vektor melyekkel eltoljuk, lehet pl.

(α, β,0,0)

, ahol

α, β = 0,1,2

. (Ezek éppen az 5. ábrán látható sík pontjai.) Ezek közül bármelyik két különböző vektor különbségének legfeljebb 2 darab nemnulla koordinátája van, ezért a különbségvektor nem lehet benne semelyik, a

0

vektort tartalmazó jó halmazban sem. Mivel összesen 8-féleképp választhatjuk

C

-t, azért ilyen módon 8 szép megoldást kapunk.

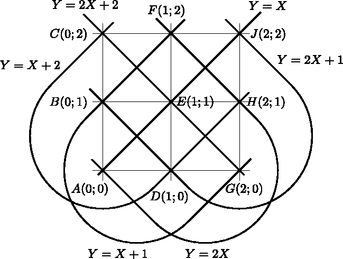5. ábra

Nézzük most azokat a szép megoldásokat, melyekben a különböző számokhoz tartozó jó halmazok nem ugyanannak a síknak az eltoltjai, azaz az

S_{i}'

halmazok közt van legalább két különböző. Ha

S_{j}' \neq S_{k}'

, akkor metszetük vagy egy pont (ami épp a

0)

, vagy egy egyenes. Az első esetben az affin tér tulajdonságai miatt azonban

S_{j} \cap S_{k}

is egy pont lenne, vagyis a két sík nem lenne diszjunkt. Tehát

S_{j}' \cap S_{k}'

egy egyenes. Viszont a

0

vektort tartalmazó jó halmazokat leíró tétel utáni feladat szerint ezek közül a halmazok közül nem választható ki 3 úgy, hogy bármelyik kettő metszete egyenes legyen. Vagyis ebben az esetben az

S_{1}, S_{2}, ..., S_{9}

síkok két különböző jó halmaz,

S_{j}'

és

S_{k}'

eltoltjai. Az

S_{j}'

és

S_{k}'

síkok meghatároznak egy őket tartalmazó

H_{0}

hipersíkot. Ez a hipersík és két eltoltja,

H_{1}

és

H_{2}

lefedi

N

-et. Továbbá

S_{j}'

és

S_{k}'

minden eltoltja teljes egészében benne van valamelyik

H_{i}

-ben, mert tetszőleges

D,E

halmazokra és

x

vektorra nyilván igaz, hogy ha

D \subset E

, akkor

(D + x) \subset (E + x)

. Ezért a

H_{i}

halmazok bármelyike csak ugyanannak a jó halmaznak az eltoltjait tartalmazhatja.
A számolási feladatainkból következik, hogy a

0

-t tartalmazó 8 jó halmaz bármelyikéhez 4 másikat tudunk választani úgy, hogy metszetük egy egyenes legyen. Így tehát összesen

8 \cdot 4 = 32

rendezett

({S'}_{j}, {S'}_{k})

párt választhatunk ki. Minden pár esetén feltehetjük, hogy az első tag eltoltjai egy, a másodiké pedig két

H_{i}

típusú hipersíkot fednek le. Ezért minden párhoz 3-3 megoldás tartozik, mert a

H_{i}

hipersíkok közül ki kell választanunk azt az egyet, melyet a pár első tagjának eltoltjaival fedünk le. Tehát ezekből a szép megoldásokból

32 \cdot 3 = 96

különböző van.
Vagyis a szép sudoku megoldások száma

8 + 96 = 104

. Ez nagyságrendekkel kevesebb, mint az összes megoldás száma, ami 5 472 730 538. S ez a szám is nagyságrendekkel kisebb, mint a

9 \times 9

-es latin négyzeteknek a cikk elején említett száma.
Végül még két feladatot adunk.

Feladat. Töltsük ki a 6. ábrán látható sudoku táblát úgy, hogy szép megoldást kapjunk.

6. ábra

Feladat. Mutassuk meg, hogy a páronként ortogonális sudoku megoldások száma legfeljebb

6

Hat darab páronként ortogonális sudoku megoldás létezik is, pl. a 7. ábrán láthatók (a kis téglalapok azonos pozícióiban lévő számok alkotnak egy-egy megoldást).

\begin{matrix} 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 7 & 7 & 7 & 8 & 8 & 8 & 9 & 9 & 9 \\ 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 7 & 7 & 7 & 8 & 8 & 8 & 9 & 9 & 9 \\ 7 & 4 & 9 & 8 & 5 & 7 & 9 & 6 & 8 & 1 & 7 & 3 & 2 & 8 & 1 & 3 & 9 & 2 & 4 & 1 & 6 & 5 & 2 & 4 & 6 & 3 & 5 \\ 5 & 6 & 8 & 6 & 4 & 9 & 4 & 5 & 7 & 8 & 9 & 2 & 9 & 7 & 3 & 7 & 8 & 1 & 2 & 3 & 5 & 3 & 1 & 6 & 1 & 2 & 4 \\ 4 & 7 & 5 & 5 & 8 & 6 & 6 & 9 & 4 & 7 & 1 & 8 & 8 & 2 & 9 & 9 & 3 & 7 & 1 & 4 & 2 & 2 & 5 & 3 & 3 & 6 & 1 \\ 9 & 8 & 6 & 7 & 9 & 4 & 8 & 7 & 5 & 3 & 2 & 9 & 1 & 3 & 7 & 2 & 1 & 8 & 6 & 5 & 3 & 4 & 6 & 1 & 5 & 4 & 2 \\ 3 & 2 & 8 & 1 & 3 & 9 & 2 & 1 & 7 & 6 & 5 & 2 & 4 & 6 & 3 & 5 & 4 & 1 & 9 & 8 & 5 & 7 & 9 & 6 & 8 & 7 & 4 \\ 6 & 9 & 5 & 4 & 7 & 6 & 5 & 8 & 4 & 9 & 3 & 8 & 7 & 1 & 9 & 8 & 2 & 7 & 3 & 6 & 2 & 1 & 4 & 3 & 2 & 5 & 1 \\ 9 & 5 & 4 & 7 & 6 & 5 & 8 & 4 & 6 & 3 & 8 & 7 & 1 & 9 & 8 & 2 & 7 & 9 & 6 & 2 & 1 & 4 & 3 & 2 & 5 & 1 & 3 \\ 7 & 2 & 3 & 8 & 3 & 1 & 9 & 1 & 2 & 1 & 5 & 6 & 2 & 6 & 4 & 3 & 4 & 5 & 4 & 8 & 9 & 5 & 9 & 7 & 6 & 7 & 8 \\ 6 & 8 & 3 & 4 & 9 & 1 & 5 & 7 & 2 & 9 & 2 & 6 & 7 & 3 & 4 & 8 & 1 & 5 & 3 & 5 & 9 & 1 & 6 & 7 & 2 & 4 & 8 \\ 2 & 4 & 7 & 3 & 5 & 8 & 1 & 6 & 9 & 5 & 7 & 1 & 6 & 8 & 2 & 4 & 9 & 3 & 8 & 1 & 4 & 9 & 2 & 5 & 7 & 3 & 6 \\ 2 & 3 & 6 & 3 & 1 & 4 & 1 & 2 & 5 & 5 & 6 & 9 & 6 & 4 & 7 & 4 & 5 & 8 & 8 & 9 & 3 & 9 & 7 & 1 & 7 & 8 & 2 \\ 8 & 5 & 9 & 9 & 6 & 7 & 7 & 4 & 8 & 2 & 8 & 3 & 3 & 9 & 1 & 1 & 7 & 2 & 5 & 2 & 6 & 6 & 3 & 4 & 4 & 1 & 5 \\ 8 & 6 & 2 & 9 & 4 & 3 & 7 & 5 & 1 & 2 & 9 & 5 & 3 & 7 & 6 & 1 & 8 & 4 & 5 & 3 & 8 & 6 & 1 & 9 & 4 & 2 & 7 \\ 3 & 7 & 4 & 1 & 8 & 5 & 2 & 9 & 6 & 6 & 1 & 7 & 4 & 2 & 8 & 5 & 3 & 9 & 9 & 4 & 1 & 7 & 5 & 2 & 8 & 6 & 3 \\ 5 & 9 & 7 & 6 & 7 & 8 & 4 & 8 & 9 & 8 & 3 & 1 & 9 & 1 & 2 & 7 & 2 & 3 & 2 & 6 & 4 & 3 & 4 & 5 & 1 & 5 & 6 \\ 4 & 3 & 2 & 5 & 1 & 3 & 6 & 2 & 1 & 7 & 6 & 5 & 8 & 4 & 6 & 9 & 5 & 4 & 1 & 9 & 8 & 2 & 7 & 9 & 3 & 8 & 7 \end{matrix}

7. ábra

Irodalomjegyzék

[1]	Bailey, R., Cameron, P. J. és Connelly, R.: Sudoku, gerechte designs, resolutions, affine space, reguli and Hamming codes, Amer. Math. Monthly (2008), 383‐404.

[2]	Kiss Gy.: Hogyan nyerjünk a TOTÓ-n? KöMaL, 57 (2007), 267‐273.

[3]	Kiss Gy. és Szőnyi T.: Véges geometriák, Polygon Kiadó (Szeged, 2001).

^{$^{*}$}A cikk elkészítését az NK 67867 és a K 81310 számú OTKA pályázat támogatta.