Kezdőlap


Cím:	Lehet egy közelítéssel kevesebb?
Szerző(k):	Kós Géza
Füzet:	2010/március, 174 - 180. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek
Hivatkozás(ok):	Feladatok: 2010/március: 2009. évi Eötvös fizikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 2009-es Eötvös-verseny 2. feladata a következő volt:

Kör alakú asztal közepén áll egy nagyon vékony falú, hengeres üvegváza, amelyben egy gyertya ég. A henger átmérője 12 cm, tengelye függőleges, a láng közepe 2 cm-re van a váza tengelyétől. Laci oldalról, a lánggal azonos magasságból nézi a vázát, és felfigyel arra, hogy a láng mellett a lángnak egy éles, határozott tükörképe is látszik a váza belsejében. Az asztalt körbejárva megállapítja, hogy a láng képének a szélessége és a vázához viszonyított helye folyamatosan változik.

a)

Milyen irányból nézve látszik a láng képe ugyanolyan szélesnek, mint maga a láng?

b)

Milyen pályán mozog a láng képének a közepe, miközben Laci körbejárja az asztalt?
A hengertükör leképezésére alkalmazhatjuk a gömbtükörre érvényes leképezési törvényt.

Mint a feladat szövege is utal rá, a Versenybizottság erősen leegyszerűsített megoldást várt a versenyzőktől¹. A valóságban ugyanis hengertükör sohasem ad egyszerre vízszintes és függőleges irányban is éles képet, és a gömbtükrökre vonatkozó leképezési törvény

(\frac{1}{t} + \frac{1}{k} = \frac{1}{f})

is csak abban az esetben érvényes, ha a tárgyról kiinduló fény a tükörről közelítőleg merőlegesen visszaverődve jut a szemünkbe.
Ebben a cikkben megvizsgáljuk, hogyan lehetett volna a feladatot pontosabban, kevesebb közelítéssel megoldani.

A kép helye attól is függ, milyen irányból nézzük

A versenyfeladat szövege a kép szélességére és a kép közepének ‐ vízszintes síkbeli ‐ pályájára vonatkozott, ezért is helyettesítette a hengertükröt gömbtükörrel. A feladatot tehát egy vízszintes síkmetszetben oldjuk meg.
Ha megrajzoljuk a tükör egy belső pontjából kiinduló, majd visszaverődő fénysugarakat, láthatjuk, hogy azok nem egyesülnek egy képpontban (1. ábra). Jól ismert tény, hogy a tükörről visszaverődő sugarak vagy azok meghosszabbításai csak nagyon speciális esetekben mennek át egy ponton: akkor, ha a tükör vagy sík, vagy pedig egy kúpszelet, a két pont pedig a kúpszelet két fókusza. A gömb esetén a két fókusz egybeesik a geometriai középpontban.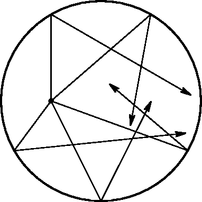

1. ábra

Ennek ellenére mégis láthatunk többé-kevésbé éles képet akkor is, ha nem merőleges irányból nézünk a tükörbe, ugyanis a visszavert fénysugaraknak csak egy nagyon vékony nyalábja jut a szemünkbe. Hamarosan látni fogjuk, hogy ezek viszont ,,majdnem'' egy ponton mennek át (2. ábra). A képpont helye azonban függ attól, hogy milyen irányból nézünk.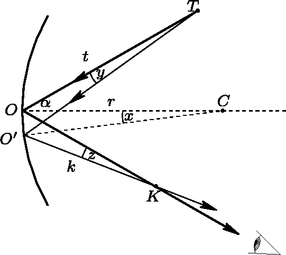

2. ábra

Egy szemmel nézve nem mindig érzékeljük pontosan a képpontnak a távolságát. Ha viszont két szemmel, viszonylag nagy távolságból nézünk, akkor két különálló, de még mindig viszonylag kis szögben érkező nyaláb metszéspontjában látjuk a képet, a kép helye közelítőleg ugyanott lesz, és a távolságot is jobban érzékeljük.

Leképezési törvény, ha nem szemből nézünk a tükörbe

A tankönyvi számításokban általában csak azt az esetet szoktuk vizsgálni, amikor a tükör egy lapos, kis középponti szögű gömbsüveg, a tárgy (és a kép) pedig közel van a tükör forgástengelyéhez. Ezt a forgástengelyt szoktuk a tükör optikai tengelyének nevezni. A számításokban kizárólag nagyon kicsi szögek fordulnak elő; a szögek koszinuszát gyakran 1-gyel becsüljük, a szögek szinuszát és tangensét pedig magukkal a szögekkel.
Minél nagyobbak a szögek, az alkalmazott közelítések annál nagyobb leképezési hibákhoz vezetnek. Szférikus aberrációnak nevezik azt a jelenséget, hogy a tükör tengelyével párhuzamosan érkező, majd a tükörről visszaverődő sugarak nem pontosan a fókuszponton mennek át. Az egy pontból vagy egymással párhuzamosan érkező, de a tengellyel nagy szöget bezáró fénysugarak sem egy ponton keresztül verődnek vissza; ezt nevezik kómának.
Most kiszámoljuk a kép helyét abban az esetben, amikor a fény nem merőlegesen érkezik a tükörre. Láttuk, hogy a kép helye attól is függ, hogy a tükör melyik pontjának közelében visszaverődő fény jut a szemünkbe. Jelöljük ez a pontot

O

-val, és legyen

α

O

pontbeli beesési szög. Jelöljük a tükör görbületi sugarát

r

-rel, a gömb középpontját

C

-vel, a megfigyelt tárgypontot pedig

T

-vel (3. ábr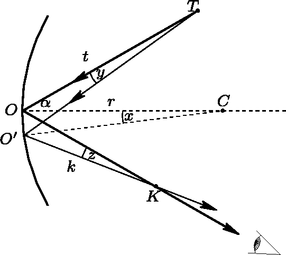a).

3. ábra

Kövessünk nyomon egy második fénysugarat is, ami az

O'

pontban verődik vissza. Legyen a két visszavert fénysugár metszéspontja

K

. Legyen

t = O T

és

k = O K

‐ ezeket nevezhetjük tárgy-, illetve képtávolságnak is. Végül legyen

\begin{matrix} O C O' ∢ = x, O T O' ∢ = y és O K O' ∢ = z . \end{matrix}

Mivel csak egy vékony fénynyalábot vizsgálunk, az

x

y

és

z

szögek kicsik, és az

O O'

szakaszt helyettesíthetjük egy függőleges szakasszal. A

C O O'

T O O'

K O O'

háromszögekben

\begin{matrix} O O' \approx r x, O O' \approx \frac{T O sin y}{cos α} \approx \frac{t y}{cos α}, illetve O O' \approx \frac{K O sin z}{cos α} \approx \frac{k z}{cos α} . \end{matrix}

T O C O'

és

C O K O'

hurkolt négyszögekből

\begin{matrix} T O' C ∢ = T O C ∢ + O T O' ∢ - O C O' ∢ = α + y - x, \\ K O' C ∢ = K O C ∢ + O C O' ∢ - O K O' ∢ = α + x - z . \end{matrix}

Mivel az

O'

pontban beeső és visszaverődő fénysugarak ugyanakkora szöget zárnak be az

C O'

iránnyal,

\begin{matrix} α + y - x = T O' C ∢ = K O' C ∢ = α + x - z, \\ y + z = 2 x, \\ \frac{O O' cos α}{t} + \frac{O O' cos α}{k} \approx 2 \frac{O O'}{r}, \\ \frac{1}{t} + \frac{1}{k} \approx \frac{2}{r cos α} . \end{matrix}

Az eredmény nem függ az

O'

pont megválasztásától. Az

O

pont közelében visszaverődő fénysugarak tehát (közelítőleg) ugyanazon a

K

ponton mennek át. Az

f = r / 2

fókusztávolságot is behelyettesítve, a nagy

α

értékek esetén is érvényes leképezési törvény:

\begin{matrix} \frac{1}{t} + \frac{1}{k} = \frac{1}{f cos α} . \end{matrix}

(1)

Az érdeklődő Olvasóra bízzuk annak végiggondolását, hogy a levezetés domború tükör (

r < 0

) és látszólagos kép (

k < 0

) esetén is elvégezhető, és ugyanerre az eredményre vezet.

Mekkora a nagyítás?

A legtöbb optikai rendszerben a képet valamilyen, a tengelyre merőleges felületre (filmre, vetítővászonra, félvezetőre vagy éppen látóidegre) vetítjük. Ennek megfelelően a tankönyvek a nagyítás mértékét csak az optikai tengelyre merőleges irányokban szokták meghatározni.
Megjegyezzük, hogy a tengellyel párhuzamos és a tengelyre merőleges irányokban a nagyítás különböző. A leképezési törvény differenciálásával láthatjuk, hogy a nagyítás a tengely irányában

{(k / t)}^{2}

, szemben a tengelyre merőleges irányokban érvényes

k / t

értékkel. A kép és a tárgy tehát általában geometriailag nem is hasonló, de a torzulás csak a megfigyelési irányban jelentkezik. Abban az esetben, amikor

k \approx t

, például ha egy homorú gömbtükör görbületi középpontjának közelében van a tükörhöz képest nagyon kisméretű tárgy, akkor a kép alakja nem is nyúlik meg vagy lapul össze. Valamekkora torzulás ilyenkor is fellép, de ennek mértéke a tárgy és a kép méretével együtt csökken.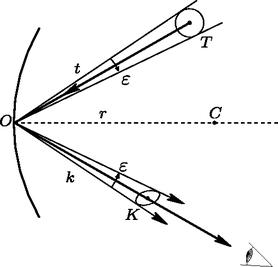

Most megvizsgáljuk, hogy a 3. ábrán látott elrendezésben mekkora a nagyítás a fénysugár irányára merőlegesen. Helyezzünk el egy kis méretű tárgyat a

T

pontban, és vizsgáljuk ennek képét, ami a

K

pont körül helyezkedik el (4. ábra). A tárgy méretén az

O T

egyenesre merőleges kiterjedését értjük (amekkorának az

T O

félegyenes irányából látnánk), a kép méretén pedig az

O K

egyenesre merőleges kiterjedését fogjuk érteni.

4. ábra

O

pontban visszaverődő sugarakat nyomon követve láthatjuk, hogy az

O

pontból a tárgy és a kép ugyanakkora

ε

szögben látszik, függetlenül attól, hogy a kép alakja miként torzul el. Mivel a tárgy és a kép is kis méretű, az

O

-tól mért távolságokat a tárgy esetében

t

-vel, a kép esetében

k

-val becsülhetjük. A tárgy

O T

-re merőleges kiterjedése tehát közelítőleg

t ε

, a kép

O K

-ra merőleges kiterjedése pedig

k ε

. A fénysugár útjára merőleges nagyítás tehát az általános esetben is

\begin{matrix} N = \frac{k}{t} . \end{matrix}

Az Eötvös-feladat pontosabb megoldása

Most már minden eszköz rendelkezésünkre áll a feladat megoldásához.

a)

részben azokat az eseteket keressük, amikor a nagyítás

1

, azaz

k = t

. Legyen ismét

C

a kör középpontja,

O

az a pont, amelynek közelében visszaverődő fény a szemünkbe jut,

α

pedig a beesési szög az

O

pontban. A

k = t

feltétel akkor teljesül, ha az

O C T

és

O C K

háromszögek egybevágóak (5. ábra).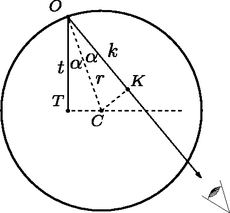

5. ábra

Az (1) módosított leképezési törvényből

\begin{matrix} \frac{2}{r cos α} = \frac{1}{t} + \frac{1}{k} = \frac{2}{t} = \frac{2}{k}, azaz t = k = r cos α . \end{matrix}

Ez pontosan akkor teljesül, ha

O T C ∢ = O K C ∢ = 90^{\circ}

. Az

α

szöget az

O C T

és

O C K

háromszögekből könnyen kiszámíthatjuk:

\begin{matrix} α = arcsin \frac{C T}{O C} = arcsin \frac{1}{3} \approx 19, 47^{\circ} . \end{matrix}

A gyertyaláng képét tehát akkor látjuk a valódi lánggal azonos szélességűnek, amikor a

K O

megfigyelési irány

90^{\circ} + 2 α \approx 128, 94^{\circ}

szöget zár be a

T C

iránnyal.

A feladat

b)

részében a kép pályáját nem lenne nehéz paraméteres görbeként felírni. Ha a 6 egység sugarú henger közepét választjuk origónak, és a gyertya a

(- 2,0)

pontban van, a

\vec{C O}

vektor iránya

φ

, akkor az

O

pontot, a

cos α

k

t

mennyiségeket, végül a

K

pontot is kifejezhetjük

φ

-vel. Magát a görbét a 6. ábrán láthatjuk.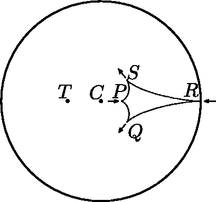

6. ábra

A láng pályája nem sima, négy pontban is megtörik. A négy ,,csúcs'' mellett nyilakkal jelöltük a megfelelő megfigyelési irányokat. Mind a négy csúcs különleges: amikor ,,vízszintesen'', a

T C

egyenes irányából nézzük a lángot, a kép a

P

, illetve

R

pontban van,

Q

és

S

pedig éppen azok a pontok, ahol a lánggal azonos szélességű képet láthatunk.

A megoldás végén érdemes összefoglalni, hogy milyen közelítéseket alkalmaztunk.
‐ A módosított leképezési törvény levezetésében elhanyagoltuk a szemünkbe érkező fénysugár átmérőjét, két szemmel történő megfigyelés esetén pedig a két megfigyelési irány által bezárt szöget.
‐ A nagyítás levezetésében elhanyagoltuk a láng átmérőjét, és vele az

α

szög fellépő értékei közötti különbségeket.
‐ Szintén a nagyítás kiszámításakor a kép méretének az

O K

-ra merőleges kiterjedését tekintettük, és nem azt vizsgáltuk, hogy szemünkkel mekkora szögben látjuk a képet.

Mi a helyzet a térben?

Eddig mindent vízszintes síkban vizsgáltunk. A térben egy dimenzióval több áll rendelkezésre ‐ azért, hogy a dolgok elromolhassanak. Vizsgáljuk meg, mi történik, ha egy hengertükörbe nézünk, mint például az Eötvös-feladatban. A 7. ábra szemlélteti, hogy viselkednek a

T

pontból induló, és a hengerről visszaverődő fénysugarak. A vizsgált fénynyaláb az

A B D C

négyszögön verődik vissza.

7. ábra

A függőleges síkokban érkező fénysugarak hasonlóan viselkednek, mint síktükör esetében. A visszavert fénysugarak meghosszabbításai egy ponton mennek át a tükör mögött. Mindegyik függőleges síkon belül keletkezik egy-egy látszólagos kép, de a képpontok helye minden síkban más és más. A képpontok egy körívet (

K_{A B} K_{C D}

) alkotnak.
A tükör vízszintes szeletein visszaverődő fénysugarak hasonlóan viselkednek, mint a vízszintes síkban. Ha a megfigyelési irányt rögzítjük, akkor minden szelethez keletkezik egy (valódi vagy látszólagos) képpont, ezek viszont egy függőleges szakaszon (

K_{A C} K_{B D}

) helyezkednek el.
Ezt a jelenséget, amely gömbtükrök és lencsék alkalmazásánál is előfordul, asztigmatizmusnak nevezik. Gömbtükör esetén például kizárólag a gömb középpontjának irányában kapunk éles képet; minél távolabbi irányba nézünk, annál elmosódottabb lesz a kép (lásd első borító).
Mivel szemünkkel csak egy nagyon keskeny fénynyalábot látunk, a kép elmosódottsága nem mindig feltűnő. A jelenség látványosabb fényképek készítésekor, mert a kameránk blendéjének átmérője nagyobb, mint az emberi pupilla. A nagy látószögű objektívekhez különleges lencséket használnak az asztigmatizmus kiküszöbölésére.

Végül gondoljunk bele, mi történik, ha két szemmel nézünk a hengertükörbe. A feladatbeli gyertyalángról mindkét szemünkkel enyhén elmosódott képet látunk. Ha fejünket függőlegesen tartjuk, a két szemünk egy magasságban van. Ha például a 7. ábrán az

A

és

C

pontok közelében visszavert fénysugarak jutnak szemünkbe, egy valódi képet láthatunk a

K_{A C}

pontban. Ha viszont fejünket

90^{\circ}

-kal oldalra döntjük, elérhetjük, hogy az

A

és

B

pontokban visszavert fény jusson a szemünkbe, így a (látszólagos) kép a

K_{A B}

pont lesz.
Rossz hír, hogy a többi esetben, ha fejünket csak kicsit döntjük oldalra, a kétféle visszaverődő sugárnyaláb nem fogja metszeni egymást; amit látunk, az nem csak elmosódott, de még szellemképes is lesz. (A szellemképeken kancsalítással segíthetünk; Süsü, a sárkány előnyben.) A kép helye és minősége nem csak attól függ, hogy honnan nézzük, hanem még attól is, hogy milyen irányban tartjuk a fejünket.

¹A versenyről a beszámoló lapunk 165. oldalán olvasható.