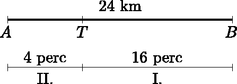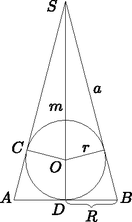Cím:	Megoldásvázlatok a 2007/4. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Juhászné Kunstár Mária ,  Marczis György ,  Mihály Mária ,  Székely András ,  Tóth István
Füzet:	2007/május, 273 - 280. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Az egymástól 24 km távolságra lévő $A$ és $B$ városból egyszerre indul egymással szembe két gépkocsi. Találkozásuk után $4$ perccel az a gépkocsi, amelyik a $B$ városból indult, megérkezik az $A$ városba, a másik pedig a találkozás után $16$ perccel a $B$ városba. Határozzuk meg a gépkocsik sebességét.  (11 pont)   Megoldás.     Foglaljuk adatainkat táblázatba (a zárójelben lévő számok a táblázat kitöltésének sorrendjét mutatják): ${\displaystyle \begin{array}{|cccccccc|}\hline \hfill {\displaystyle }& \multicolumn{2}{c}{{\displaystyle \text{út (km)}}}& \multicolumn{2}{c}{{\displaystyle \text{sebesség (km/óra)}}}& \multicolumn{3}{c}{{\displaystyle \text{idő (óra)}}}\\ \hfill {\displaystyle \text{I. <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mi>T</mi></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>15</mn></mrow></mfrac></mrow><mi>y</mi></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="15pt" depth="10pt" width="0pt"></mspace></math>}}& \hfill {\displaystyle \text{(7)}}& \hfill {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}& \hfill {\displaystyle \text{(9)}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>15</mn></mrow></mfrac></mrow><mo>⋅</mo><mrow><mfrac><mrow><mi>y</mi></mrow><mrow><mi>x</mi></mrow></mfrac></mrow></math>}}\hfill & {\displaystyle \text{találkozás előtt}}\hfill & \hfill {\displaystyle \text{(11)}}\\ \hfill {\displaystyle \text{II. <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mi>T</mi></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>15</mn></mrow></mfrac></mrow><mi>x</mi></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="15pt" depth="10pt" width="0pt"></mspace></math>}}& \hfill {\displaystyle \text{(8)}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>}}& \hfill {\displaystyle \text{(10)}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>15</mn></mrow></mfrac></mrow><mo>⋅</mo><mrow><mfrac><mrow><mi>x</mi></mrow><mrow><mi>y</mi></mrow></mfrac></mrow></math>}}\hfill & {\displaystyle \text{találkozás előtt}}\hfill & \hfill {\displaystyle \text{(12)}}\\ \hfill {\displaystyle \text{I. <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>T</mi><mi>B</mi></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>15</mn></mrow></mfrac></mrow><mi>x</mi></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="15pt" depth="10pt" width="0pt"></mspace></math>}}& \hfill {\displaystyle \text{(5)}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}& \hfill {\displaystyle \text{(3)}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>16</mn></mrow><mrow><mn>60</mn></mrow></mfrac></mrow></math>}}\hfill & {\displaystyle \text{találkozás után}}\hfill & \hfill {\displaystyle \text{(1)}}\\ \hfill {\displaystyle \text{II. <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>T</mi><mi>A</mi></math>}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>15</mn></mrow></mfrac></mrow><mi>y</mi></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="15pt" depth="10pt" width="0pt"></mspace></math>}}& \hfill {\displaystyle \text{(6)}}& \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>}}& \hfill {\displaystyle \text{(4)}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>4</mn></mrow><mrow><mn>60</mn></mrow></mfrac></mrow></math>}}\hfill & {\displaystyle \text{találkozás után}}\hfill & \hfill {\displaystyle \text{(2)}}\\ \hline\end{array}}$ Mivel a két autó egyszerre indult, azért a találkozásig eltelt idők egyenlők: $\begin{array}{c}{\displaystyle \frac{1}{15}\cdot \frac{y}{x}=\frac{4}{15}\cdot \frac{x}{y}\mathrm{,}\text{ azaz }{\left(\frac{y}{x}\right)}^2=4.}\end{array}$ Amiből $y=2x$, vagy $y=-2x$. Ez utóbbi nem felel meg a szöveg tartalmának, ezért nem adhat megoldást. Mivel a teljes út 24 km, így $\frac{1}{15}\cdot 2x+\frac{4}{15}x=24$, amiből $x=60$, s ekkor $y=120$. Tehát az $A$ városból induló autó sebessége 60 km/óra, a $B$ városból indulóé 120 km/óra.   2. $a)$ $1000$ almát úgy akarunk $k$ $\left(k\ge 2\right)$ tanuló között szétosztani, hogy az első tanuló kapjon $x$ almát és minden további tanuló rendre $3$-mal kevesebbet mindaddig, míg az $1000$ almát maradéktalanul ki nem osztottuk. Hány tanulóról lehet szó? Hány alma jut ekkor az utolsó tanulónak? $b)$ Legközelebb $16$ ember között az $1000$ almát úgy szeretnénk elosztani, hogy az első $11$ embernek egyforma számú almát adjunk, de ezt követően $50\%$-kal mindig többet, mint az előzőnek. Ekkor a végén marad még $15$ alma. Az egyes emberek által kapott almák számát feljegyezzük, s így kapunk $16$ adatot. Mennyi az így kapott adatok átlaga és módusza?  (12 pont)   Megoldás. $a)$ A jelöléseket használva: $\begin{array}{c}{\displaystyle S_k=x+\left(x-3\right)+\left(x-6\right)+\text{...}+\left[x-3\left(k-1\right)\right]=\frac{2x-3\left(k-1\right)}{2}\cdot k=\mathrm{1000,}}\end{array}$ azaz $\left[2x-3\left(k-1\right)\right]\cdot k=2^4\cdot 5^3$. Ha $k$ páros, akkor $2x-3\left(k-1\right)$ páratlan és viszont. Ezt figyelembe véve a törzstényezős szorzatalakok közül a feladat feltételeinek csak a következők tesznek eleget: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cccc}\hfill {\displaystyle 400\cdot \mathrm{5,}}& \hfill {\displaystyle \text{ekkor}}& {\displaystyle k=5;}\hfill & {\displaystyle x=\mathrm{206,}}\hfill \\ \hfill {\displaystyle 80\cdot \mathrm{25,}}& \hfill {\displaystyle \text{ekkor}}& {\displaystyle k=25;}\hfill & {\displaystyle x=\mathrm{76,}}\hfill \\ \hfill {\displaystyle 125\cdot \mathrm{16,}}& \hfill {\displaystyle \text{ekkor}}& {\displaystyle k=16;}\hfill & {\displaystyle x=85.}\hfill \end{array}}}\end{array}$ A következő lehetőségeket kaptuk: 5 tanuló esetén az utolsó 194, 25 tanuló esetén az utolsó 4, és 16 tanuló esetén az utolsó 40 almát kap. $b)$ Az adatok átlagának kiszámításához nem szükséges az összes adatot ismernünk. Tudjuk ugyanis a 16 adat összegét, ami 985. Ekkor az átlag: $\frac{985}{16}=61\mathrm{,}5625$. A 16 adat utolsó 6 tagja egy mértani sorozat egymást követő hat eleme lesz, ahol $q=1\mathrm{,}5$ és az első elem ismeretlen, jelöljük ezt $a$-val. Felírható a következő egyenlet: $10a+a\cdot \frac{1\mathrm{,}{5}^6-1}{1\mathrm{,}5-1}+15=1000$. Ebből $a=32$ adódik. Ez a legtöbbször feljegyzett adat, így a minta módusza 32.   3. Oldjuk meg a következő egyenleteket: $a)$ $\frac{x^2+2x+1}{\sqrt[]{{\left(x+1\right)}^2}}+x+1=0$; $b)$ ${10}^{\text{lg}3x}=2x-3$; $c)$ $\sqrt[]{x-1}\cdot \sqrt[]{x+5}=\sqrt[]{x^2+4x-5}$; $d)$ $\sqrt[]{1-\text{sin}{}^{2}x}\cdot \text{tg}x=\text{sin}x$.  (14 pont)   Megoldás. $a)$ Az egyenlet nincs értelmezve, ha $x=-1$. Mivel $\sqrt[]{{\left(x+1\right)}^2}=|x+1|$, azért az egyenletet a következő alakban írjuk: $\begin{array}{c}{\displaystyle \frac{{\left(x+1\right)}^2}{|x+1|}=-\left(x+1\right)\mathrm{.}}\end{array}$ Mivel $x\ne -1$, azért $\frac{x+1}{|x+1|}=-1$. Ezek szerint $|x+1|$ az $x+1$ ellentettjével egyenlő, ezért $x+1<0$. Vagyis $x<-1$ valós számok az egyenlet megoldásai. $b)$ Az egyenlet bal oldala csak akkor értelmezhető, ha $x>0$. Ekkor $3x=2x-3$. Így $x=-3$, ami nem eleme az értelmezési tartománynak. Az egyenletnek nincs megoldása. $c)$ Az egyenlet csak akkor értelmezhető, ha $x\ge 1$ (a négyzetgyökök miatt). Ekkor az egyenlet azonosság, vagyis a megoldása: $x\ge 1$ valós számok. $d)$ Mivel $\sqrt[]{1-\text{sin}{}^{2}x}=|\text{cos}x|$, azért az egyenlet $\begin{array}{c}{\displaystyle \frac{\text{sin}x}{\text{cos}x}|\text{cos}x|=\text{sin}x}\end{array}$ alakban írható. Két eset van. I. $\text{sin}x=0$. Ekkor $x_1=k_1\pi$, akol $k_1\in \text{Z}$. II. $|\text{cos}x|=\text{cos}x$. Mivel $\text{cos}x\ne 0$, így $\text{cos}x>0$. Ekkor $\begin{array}{c}{\displaystyle -\frac{\pi }{2}+2k_2\pi <x_2<\frac{\pi }{2}+2k_2\pi \mathrm{,}\text{ ahol }{k}_2\in \text{Z}\mathrm{.}}\end{array}$   4. Egy paralelogramma egyik átlójának hossza egy bizonyos szög szinuszával, a másik ugyanennek a szögnek a koszinuszával, míg a rövidebbik oldala a szög kétszeresének szinuszával egyenlő. A két átló által bezárt szög ${60}^{\circ }$. Számoljuk ki a paralelogramma oldalhosszainak pontos értékét.  (14 pont)   Megoldás. Mivel a paralelogramma átlói felezik egymást, azért az $MBC$ háromszögben $MB=\frac{\text{sin}\alpha }{2}$ és $MC=\frac{\text{cos}\alpha }{2}$. A rövidebbik oldala a paralelogrammának $BC$, így $BC=\text{sin}2\alpha$. Az $MBC$ háromszögre felírjuk a koszinusz-tételt, majd rendezzük a kapott egyenletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(\frac{\text{sin}\alpha }{2}\right)}^2+{\left(\frac{\text{cos}\alpha }{2}\right)}^2-2\cdot \frac{\text{sin}\alpha }{2}\cdot \frac{\text{cos}\alpha }{2}\cdot \text{cos}{60}^{\circ }}& {\displaystyle =\text{sin}{}^{2}2\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\text{sin}{}^2\alpha +\text{cos}{}^2\alpha }{4}-\frac{2\cdot \text{sin}\alpha \cdot \text{cos}\alpha }{4}\cdot \frac{1}{2}}& {\displaystyle =\text{sin}{}^{2}2\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{1}{4}-\frac{1}{8}\cdot \text{sin}2\alpha =\text{sin}{}^{2}2\alpha \mathrm{,}0=\text{sin}{}^{2}2\alpha +\frac{1}{8}}& {\displaystyle \cdot \text{sin}2\alpha -\frac{1}{4}\mathrm{.}}\hfill \end{array}}$ A $\text{sin}2\alpha$-ra kapott két gyök egyike negatív, így $BC=\text{sin}2\alpha =\frac{-1+\sqrt[]{65}}{16}\approx 0\mathrm{,}44$.       Felírjuk a koszinusz-tételt az $AMB$ háromszögre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A{B}^2}& {\displaystyle ={\left(\frac{\text{sin}\alpha }{2}\right)}^2+{\left(\frac{\text{cos}\alpha }{2}\right)}^2-2\cdot \frac{\text{sin}\alpha }{2}\cdot \frac{\text{cos}\alpha }{2}\cdot \text{cos}{120}^{\circ }=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\text{sin}{}^2\alpha +\text{cos}{}^2\alpha }{4}+\frac{2\cdot \text{sin}\alpha \cdot \text{cos}\alpha }{4}\cdot \frac{1}{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{4}+\frac{1}{8}\cdot \text{sin}2\alpha =\frac{1}{4}+\frac{1}{8}\cdot \frac{-1+\sqrt[]{65}}{16}=\frac{32-1+\sqrt[]{65}}{128}=\frac{31+\sqrt[]{65}}{128}\mathrm{.}}\hfill \end{array}}$ Vagyis $AB=\sqrt[]{\frac{31+\sqrt[]{65}}{128}}\approx 0\mathrm{,}55$.   II. rész   5. Egy biológushallgató két tárgylemez közt lévő vizes közeget figyel mikroszkóppal, amely egy 0,9 mm oldalú négyzet alakú területet foglal el. Ezen négyzet oldalainak harmadával megegyező oldalhosszúságú, $9$ négyzetből álló négyzethálót vetít rá a látótérre, amely sakktáblaszerűen szürkével és fehérrel színezett úgy, hogy a bal alsó sarok szürke. Legyen két eseményünk az, hogy amikor először a mikroszkópba néz, akkor egy pontszerű baktériumot $A$: fehér négyzetben lát. $B$: a közeg négyzetének bal oldalához közelebb látja, mint az alsó oldalához. $a)$ Számítsuk ki a $P\left(A\right)$, $P\left(B\right)$, $P\left(\overline{A}\cdot B\right)$ valószínűségeket. $b)$ Mennyi annak a valószínűsége, hogy egy 0,01 mm sugarú gömb alakú porszemet úgy pillant meg, mintha a porszemnek lenne valamelyik szürke négyzettel közös pontja? (A porszemet a mikroszkópban egy 0,01 mm sugarú körlapnak látjuk, és az elhelyezkedése véletlenszerű a megfigyelt közegben.)  (16 pont)   Megoldás. A pontszerű baktérium az $a=0\mathrm{,}9$ mm oldalú négyzet alakú vizes közeg akármelyik pontjában előfordulhat, továbbá érvényes a megfigyelésre a geometriai valószínűség minden feltétele. $a)$ Az $A$ esemény akkor következik be, ha a baktérium a négy fehér négyzet valamelyikében van, ezért $\begin{array}{c}{\displaystyle P\left(A\right)=\frac{4}{9}\mathrm{.}}\end{array}$ A $B$ eseménynél a szaggatott átló feletti részben látható a baktérium, ezért $P\left(B\right)=0\mathrm{,}5$.     A $\overline{A}\cdot B$ eseménynél az átló feletti részbe eső szürke területek egyikében lesz a baktérium, ezért $\begin{array}{c}{\displaystyle P\left(\overline{A}\cdot B\right)=\frac{{\left(\frac{a}{3}\right)}^2+3\cdot \frac{1}{2}\cdot {\left(\frac{a}{3}\right)}^2}{a^2}=\frac{5}{18}\mathrm{.}}\end{array}$ $b)$ A porszem megfigyelésekor a porszem középpontja véletlenszerűen, de egy $b=0\mathrm{,}9-2\cdot 0\mathrm{,}01=0\mathrm{,}88$ mm oldalhosszúságú négyzetben fordulhat elő, hiszen a ,,szélső'' helyzeténél érintkezik a közeg négyzetének oldalával, ezért ekkor a középpontja az oldalaktól 0,01 mm távol van. A kérdezett esemény bekövetkezésekor valamelyik szürke négyzettel érintkezve a ,,szélső'' helyzetnél a középpont ezek oldalától 0,01 mm-re van, ezért a négy fehér négyzetben kijelölt $\begin{array}{c}{\displaystyle c=\frac{0\mathrm{,}9}{3}-2\cdot 0\mathrm{,}01=0\mathrm{,}28\text{mm }}\end{array}$ oldalú négyzet egyikében sem lehet a porszem középpontja.     Így a keresett valószínűség: $\begin{array}{c}{\displaystyle P=\frac{b^2-4\cdot c^2}{b^2}=1-\frac{4\cdot c^2}{b^2}=1-\frac{4\cdot 0\mathrm{,}{28}^2}{0\mathrm{,}{88}^2}\approx 0\mathrm{,}595.}\end{array}$   6. $a)$ Tekintsük azokat az ötjegyű számokat, amelyekre igaz, hogy utolsó három számjegyük különböző, ezen számjegyek összege $5$ és közülük egyik se prímszám. Mennyi ezek közül a $8$-cal oszthatók összege? $b)$ Tekintsük az összes olyan $n$ pozitív egész számot, amelyre $n!+3$ négyzetszám. Hány ilyen négyzetszám van?  (16 pont)   Megoldás. $a)$ A feltételeket figyelembe véve a három utolsó számjegy csak a 0, 1, 4 lehet. Ezek hat lehetséges sorrendjéből csak a 104 a megfelelő a 8-cal való oszthatóság miatt. Az első két számjegy helyére kilencven kétjegyű szám kerülhet. A legkisebb jó ötjegyű az $a_1=10104$ és minden további $d=1000$-rel több. A 90 elemű számtani sorozat összege: $\begin{array}{c}{\displaystyle S_{90}=\frac{90}{2}\left[2\cdot 10104+89\cdot 1000\right]=4914360.}\end{array}$ $b)$ Ha $n\ge 5$, akkor $n!$ utolsó számjegye 0, így $n!+3$ utolsó számjegye 3. A négyzetszámok viszont nem végződhetnek 3-ra. Ebből adódóan csak $n=4$-ig kell vizsgálódni. Ezekből négyzetszámot ad az $n=1$ és az $n=3$. Vagyis két megfelelő négyzetszámot találtunk, a 4-et és a 9-et.   7. Az $A\left(-2;0\right)$ és a $B\left(2;0\right)$ pont egy derékszögű háromszög átfogójának két végpontja. $a)$ Határozzuk meg a harmadik csúcspont koordinátáit, ha az $A$ csúccsal szemközti befogó hossza $2$. $b)$ A $B$ középpontú $2$ sugarú kör egy olyan háromszög beírható köre, amelynek egyik csúcspontja az $A$ pont, és az $A$ ponttal szemközti oldal az $E\left(2+\sqrt[]{3};1\right)$ pontban érinti a kört. Határozzuk meg e háromszög másik két csúcspontjának koordinátáit. $c)$ Mekkorák a keresett háromszög szögei?  (16 pont)   Megoldás. Készítsünk ábrát.     $a)$ Két ilyen háromszög van. Ezek egymás tükörképei az $x$ tengelyre vonatkozóan. Mivel $AB=2\cdot B{C}_1$, azért $C_{1}AB\sphericalangle ={30}^{\circ }$, azaz $A{C}_1=2\sqrt[]{3}$, így $C_1\left(1;\sqrt[]{3}\right)$ és $C_2\left(1;-\sqrt[]{3}\right)$. $b)$ Az ${\left(x-2\right)}^2+y^2=4$ egyenletű kört érintő háromszög két oldalának egyenese az $A$ pontból a körhöz húzott két érintő. Az $E$ pont rajta van a körön, mert koordinátái kielégítik a kör egyenletét. A harmadik oldal egyenese a kör $E$ pontjához tartozó érintő lesz. Az $A$ ponton áthaladó érintők egyenletéhez felírjuk a két egyenes irányvektorát: $\overrightarrow{A{C}_1}\left(3;\sqrt[]{3}\right)$, $\overrightarrow{A{C}_2}\left(3;-\sqrt[]{3}\right)$. A két oldal egyenesének egyenlete: $\begin{array}{c}{\displaystyle \sqrt[]{3}x-3y=-2\sqrt[]{3}\text{ és }\sqrt[]{3}x+3y=-2\sqrt[]{3}\mathrm{.}}\end{array}$ Az $E$ ponthoz tartozó érintő egyenletéhez felírjuk az egyenes normálvektorát: $\overrightarrow{BE}\left(\sqrt[]{3};1\right)$. Az egyenes egyenlete: $\sqrt[]{3}x+y=2\sqrt[]{3}+4$. A metszéspontokat megkapjuk, ha kiszámítjuk ennek az egyenesnek a másik két egyenessel való metszéspontját. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{3}x-3y}& {\displaystyle =-2\sqrt[]{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle \sqrt[]{3}x+y}& {\displaystyle =2\sqrt[]{3}+4.}\hfill \end{array}}\}}\end{array}$ Az egyenletrendszer megoldása: $x_1=1+\sqrt[]{3}$, $y_1=1+\sqrt[]{3}$. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{3}x+3y}& {\displaystyle =-2\sqrt[]{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle \sqrt[]{3}x+y}& {\displaystyle =2\sqrt[]{3}+4.}\hfill \end{array}}\}}\end{array}$ Az egyenletrendszer megoldása: $x_2=4+2\sqrt[]{3}$, $y_2=-2-2\sqrt[]{3}$. A keresett pontok koordinátái: $D\left(1+\sqrt[]{3};1+\sqrt[]{3}\right)$, $F\left(4+2\sqrt[]{3};-2-2\sqrt[]{3}\right)$. $c)$ Belátható, hogy a $B{C}_{1}DE$ négyszög négyzet, tehát a $D$ csúcsnál derékszög van, az $A$ csúcsnál levő szög ${60}^{\circ }$, az $F$ csúcsnál levő pedig ${30}^{\circ }$.   8. Egy egyenes körkúp felszínét, térfogatát és a beírt gömbjének felszínét jelölje sorra $A$, $V$ és $G$. Igazoljuk, hogy $A^{2}G=36\pi \cdot V^2$.  (16 pont)     Megoldás. A kúp alapkörének sugara $R$, magassága $m$, alkotója $a$ és a beírt gömb sugara $r$, melyekkel: $\begin{array}{c}{\displaystyle A=\pi R\left(R+a\right)\mathrm{,}V=\frac{\pi R^{2}m}{3}\mathrm{,}G=4r^2\pi \mathrm{.}}\end{array}$ A kúp tengelyén keresztül egy síkkal elmetszve a testeket, az $ABS$ egyenlő szárú háromszögben $OCS▵\sim ADS▵$, mert 2‐2 szögük megegyezik. Így $AD=R$, $DS=m$ és $OC=r$ miatt $\frac{r}{R}=\frac{m-r}{a}$, melyből $\begin{array}{c}{\displaystyle ar=Rm-Rr\mathrm{,}\text{ így }m=\frac{r\left(R+a\right)}{R}\mathrm{.}}\end{array}$ Tehát $\begin{array}{c}{\displaystyle 36\pi \cdot V^2=36\pi \cdot \frac{{\pi }^2{R}^4{m}^2}{9}=\frac{4{\pi }^3{R}^4{r}^2{\left(R+a\right)}^2}{R^2}={\pi }^2{R}^2{\left(R+a\right)}^2\cdot 4r^2\pi =A^{2}G\mathrm{.}}\end{array}$   9. Legyen adva a valós számokon értelmezett $f\left(x\right)=x-\frac{2}{3}{x}^3$ függvény. $a)$ A $\left[-2;1\right]$ intervallum mely $x$ értékei esetén veszi fel ez a függvény a maximális, illetve a minimális értékét? Mekkorák ezek az értékek? $b)$ Ezen az intervallumon hol lesz a grafikonhoz húzott érintő párhuzamos a $g\left(x\right)=-3x+2007$ függvény grafikonjával? $c)$ Mi lehet a $h\left(x\right)$ függvény hozzárendelési szabálya, ha $\begin{array}{c}{\displaystyle h\left(f\left(x\right)\right)=\sqrt[3]{x-\frac{2}{3}{x}^3}?}\end{array}$ Határozzuk meg az $f\left(h\left(x\right)\right)$ összetett függvényt.  (16 pont)   Megoldás. $a)$ Az adott folytonos és mindenütt differenciálható függvény egy véges zárt intervallumon a szélsőértékeit az intervallum végpontjaiban vagy a derivált zérushelyein veheti fel. Ezeket a helyeket kell megvizsgálni. $f\text{'}\left(x\right)=1-2x^2$. $f\text{'}\left(x\right)=0$, ha $x_{\mathrm{1,2}}=\pm \frac{\sqrt[]{2}}{2}$ (itt lehetnek az intervallum belső pontjaiban szélsőértékek). Meg kell vizsgálni a derivált előjeleit ezen értékek előtt és után. ${\displaystyle \begin{array}{|cccccc|}\hline {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2</mn><mo>≤</mo><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="15pt" depth="8pt" width="0pt"></mspace></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi><mo>≤</mo><mn>1</mn></math> }}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mo stretchy="false">'</mo><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{+}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↓</mo></math>}}\hfill & \hfill {\displaystyle \text{min}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↑</mo></math>}}\hfill & \hfill {\displaystyle \text{max}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↓</mo></math>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math> értéke}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="15pt" depth="8pt" width="0pt"></mspace></math>}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mrow><mroot><mrow><mn>2</mn></mrow><mrow></mrow></mroot></mrow></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle }\hfill \\ \hline\end{array}}$ Tehát a derivált zérushelyein $\left(x_{\mathrm{1,2}}=\pm \frac{\sqrt[]{2}}{2}\right)$ a függvénynek lokális szélsőértékei vannak. Meg kell még vizsgálni az $x=-2$ és az $x=1$ helyeken is a függvényértékeket: $f\left(-2\right)=\frac{10}{3}$ és $f\left(1\right)=\frac{1}{3}$. Összevetve ezeket az értékeket a táblázatban szereplő értékekkel, a következő megállapításokra jutottunk: Az $f\left(x\right)$ függvény a $\left[-2;1\right]$ intervallumon a maximumát az $x=-2$ helyen veszi fel: $\begin{array}{c}{\displaystyle f_{\underset{}{\overset{}{\text{max}}}}\left(-2\right)=\frac{10}{3}\mathrm{.}}\end{array}$ Az $f\left(x\right)$ függvény a $\left[-2;1\right]$ intervallumon a minimumát az $x=-\frac{\sqrt[]{2}}{2}$ helyen veszi fel: $\begin{array}{c}{\displaystyle f_{\underset{}{\overset{}{\text{min}}}}\left(-\frac{\sqrt[]{2}}{2}\right)=-\frac{\sqrt[]{2}}{3}\mathrm{.}}\end{array}$ $b)$ Az érintő meredekségét a deriváltfüggvény adott helyen vett helyettesítési értéke adja. Mivel $f\text{'}\left(x\right)=1-2x^2$, azért keressük az $1-2x^2=-3$ egyenlet megoldásait a vizsgált intervallumon. Ezek $x_{\mathrm{3,4}}=\pm \sqrt[]{2}$. Mivel az $x_4=\sqrt[]{2}$ nem eleme a $\left[-2;1\right]$ intervallumnak, ezért csak az $x_3=-\sqrt[]{2}$ helyen lesz az érintő meredeksége $-3$. $c)$ Mivel a harmadik gyök alatt éppen az $f\left(x\right)$ függvény hozzárendelési szabálya szerepel, így $h\left(x\right)=\sqrt[3]{x}$. Az így kapott $h\left(x\right)$ függvény segítségével képzett összetett függvény: $\begin{array}{c}{\displaystyle f\left(h\left(x\right)\right)=\sqrt[3]{x}-\frac{2}{3}{\left(\sqrt[3]{x}\right)}^3=\sqrt[3]{x}-\frac{2}{3}x\mathrm{.}}\end{array}$