|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A népszerű TOTÓ játékban focimeccs eredményét kell megtippelni. Nem a pontos végeredményt kell eltalálni, hanem csak azt, hogy a két csapat közül melyik nyer. Ha az otthon játszó csapat győz, akkor a helyes tipp 1, ha a vendégcsapat, akkor 2, ha pedig a meccs döntetlen, akkor . A 14. meccs eredményét csak akkor veszik figyelembe, ha az első 13 meccs mindegyikére helyes tippet adtunk. A játék szervezője minden héten kijelöli azokat a meccseket, melyek kimenetelére tippelni kell. A játék résztvevői tippeket, azaz az jelekből álló hosszú sorozatokat készítenek. Minden tippért egy előre meghatározott összeget fizetnek a szervezőnek (a magyarországi játékban jelenleg 40 Ft-ot). Miután lejátszották a meccseket, a szervező a tippekért beszedett pénz egy részét (Magyarországon kb. 50% -át) kiosztja azon játékosok közt, akik a legpontosabb előrejelzéseket adták. Általában a telitalálattal, tehát ha valaki mind a 14 meccs kimenetelét eltalálta, jelentős összeget lehet nyerni, 10-nél kevesebb találatért viszont már nem jár pénz. (A cikk írását megelőző hétvégén, 2007. április 1-jén pl. a , 13, 12, 11 és 10 találatos szelvények nyereménye rendre 347 582, 95 065, 4 440, 508 és 170 Ft volt.) Miután a szervező a játékosok által befizetett pénznek csak egy részét osztja szét nyereményként, ezért nyilván érdemesebb szervezőnek lenni, mint játékosnak. Ezen a módon azonban Magyarországon nem nyerhetünk a TOTÓ-n, mert a szervezés állami monopólium. Játékosként több lehetőség kínálkozik. Megpróbálhatunk némi pénzt adni az egyes csapatok csatárainak, hogy játsszanak az átlagosnál jobban, esetleg néhány kapust próbálhatunk arra rávenni, hogy játsszon a szokásosnál gyengébben, vagy némelyik bírót kérhetjük meg arra, hogy érdekeinknek megfelelően fújjon. Ezek azonban sportszerűtlen dolgok. Ebben a cikkben arra mutatunk néhány módszert, hogy ha a mérkőzések lehetséges kimenetelei egyforma valószínűségűek, akkor hogyan érhetünk el biztosan előre meghatározott számú találatot a lehető legkevesebb tippel.
A továbbiakban a döntetlen kimenetelt helyett 0-val jelöljük. Feladatunkat tehát kicsit általánosabb formában a következőképp fogalmazhatjuk meg:
Legyenek és rögzített természetes számok. Tekintsük az hosszú jegyekből álló sorozatok halmazát. Adjuk meg azt a lehető legkisebb elemszámú részhalmazt, melyre igaz, hogy bármely eleméhez van olyan -beli elem, amely -től legfeljebb helyen tér el.
Áttérve a matematikában szokásos elnevezésekre és jelölésekre, elemeit vektoroknak, az sorozat -edik elemét, -t pedig a vektor -edik koordinátájának nevezzük, és az jelölést használjuk.
2. A Hamming-távolság
Azt, hogy egy tippben hány hiba van, az adja meg, hogy hány olyan koordinátája van a tippvektornak, ami eltér az eredményvektor megfelelő koordinátájától. Ezért természetes módon adódik a következő definíció az -beli elemek egymástól való eltérésének mérésére:
Definíció. Az | |
-beli elemek Hamming-távolsága, azon indexek száma, melyekre teljesül.
Az így mért eltérést azért nevezik távolságnak, mert rendelkezik a geometriából ismert ,,szokásos'' távolság legfontosabb tulajdonságaival. Ezeket a következő állításban foglaljuk össze.
1. állítás. Tetszőleges vektorok Hamming-távolságára | 1. | , és egyenlőség pontosan akkor áll fenn, ha . |
(Állításunkat röviden úgy mondják, hogy az halmaz a Hamming-távolsággal ellátva metrikus teret alkot.)
Bizonyítás. Az 1. és a 2. állítás nyilvánvalóan adódik a definícióból. A 3. állítást háromszög-egyenlőtlenségnek nevezik, mert formálisan megegyezik az elemi geometriából ismert, ugyanígy nevezett állítással. Ha , akkor pontosan darab olyan koordinátája van -nek és -nek, amelyek különböznek. Tekintsük -nak az ugyanilyen indexű koordinátáit. Ezek mindegyike és megfelelő koordinátái közül legfeljebb az egyikkel egyezik meg, azaz legalább az egyiktől különbözik. Tehát ha csak ezeket a koordinátákat nézzük, már akkor is összesen legalább eltérés lesz és , illetve és közt. Attól függően, hogy a további koordinátában van vagy nincs eltérés, lesz az állításban szigorú egyenlőtlenség, illetve egyenlőség.
A távolság segítségével a ,,szokásos'' módon definiálhatjuk a gömböket.
Definíció. Adott vektor és egész szám esetén középpontú sugarú gömbnek nevezzük és -rel jelöljük azon -beli elemek halmazát, melyeknek -től való Hamming-távolsága legfeljebb . Azaz:
Az, hogy egy gömb hány vektort tartalmaz, csak a gömb sugarától függ.
2. állítás. Tetszőleges középpont körüli sugarú gömb pontosan vektort tartalmaz az halmazból.
Bizonyítás. Ha a gömb középpontja , akkor a gömb azokat a vektorokat tartalmazza, amelyek legfeljebb koordinátában térnek el -től. Ha egy vektor pontosan koordinátában különbözik -től, akkor -féleképp tudjuk kiválasztani ezt az darab koordinátát, s minden egyes koordináta helyére egymástól függetlenül azt a 2‐2 koordinátát írhatjuk, amelyek különböznek megfelelő koordinátáitól.
Ha az meccset tartalmazó TOTÓ-ban azt szeretnénk, hogy legalább találatunk legyen, akkor olyan tipphalmazt kell megjátszanunk, amelyre a középpontú sugarú gömbök uniója tartalmazza a teljes halmazt. Ha ugyanis ez teljesül, akkor tetszőleges eredmény esetén lesz olyan tippünk, amelyre , azaz tippünk a helyes eredménnyel legalább koordinátában megegyezik.
Ebből az észrevételből azonnal adódik következő tételünk, melyet gömbpakolási korlátnak neveznek:
3. tétel. Ha az meccset tartalmazó TOTÓ-ban a tipphalmazzal biztosan elérünk legalább találatot, akkor a tipphalmaz elemszámára teljesülnie kell a egyenlőtlenségnek.
Bizonyítás. A 2. állítás szerint minden sugarú gömb vektort tartalmaz. Mivel a tippek körüli gömbök uniójának tartalmaznia kell -t, ezért ha ezt a számot megszorozzuk a tippek számával, akkor eredményül legalább elemszámát, azaz -t kell kapnunk.
3. Jó tipphalmazok
Nézzünk meg először két triviális esetet. Ha biztos telitalálatot szeretnénk elérni, akkor . Tehát a tippjeink körüli 0 sugarú gömbök uniójának, azaz maguknak a tippek halmazának tartalmaznia kell -t. Vagyis biztos telitalálatot csak akkor érhetünk el, ha minden lehetőséget megjátszunk. (Ezt persze Hamming-távolság és gömbök nélkül is tudtuk.) Mit kell tennünk, ha az meccsből álló játékban biztos 5 találatot szeretnénk elérni? Legyen az a tipp, amelynek minden koordinátája . Ezzel a három tippel biztosan elérünk legalább 5 találatot, ugyanis minden 13 hosszú vektornak van legalább 5 darab egyenlő koordinátája, hiszen ha egy vektor mindhárom lehetséges koordinátából legfeljebb 4-et tartalmazna, akkor hossza legfeljebb lenne. Gömbökkel megfogalmazva állításunkat:
A TOTÓ-ban azonban az 5 találatos szelvénnyel nem lehet nyerni. Nyereményt általában csak a meccsek számával majdnem megegyező találatszámra fizetnek. Vagyis az érdekes tipphalmazok azok, melyekre értéke kicsi. A továbbiakban bevezetjük az jelölést. Ekkor a szám azt adja meg, hogy legfeljebb hány meccs eredményét hibázhatjuk el. Nagy értékekre a jó tipphalmazok megadása nagyon nehéz feladat, még akkor sincs a probléma csak néhány -re megoldva, ha . A következő táblázatban összefoglaljuk az ismert eredményeket és esetén. Az -nel jelölt sor és az -rel jelölt oszlop kereszteződésében álló első szám a legjobb ismert tipphalmaz elemszáma, az utána zárójelben szereplő szám pedig az optimális tipphalmaz méretére vonatkozó legjobb alsó becslés. Ha nincs zárójelbe írt szám, akkor az azt jelenti, hogy a konstrukció optimális, azaz be van bizonyítva, hogy kevesebb tippel nem érhető el a kívánt találatszám. A zárójelben lévő becslés legtöbbször a 3. tételben szereplő gömbpakolási korlátból következik, néhány esetben azonban jobb annál.
Látható, hogy esetén csak az , és az , párok esetén éri el a legjobb ismert konstrukció a gömbpakolási korlátból következő lehető legkisebb elemszámot. Ezekben az esetekben a konstrukciók kódelméletiek. Ezekről részletesen olvashatunk Hraskó András és Szőnyi Tamás [2] cikkében. Némelyik tipphalmaz (kicsi értékekre) a cikk végén található feladatok segítségével állítható elő. Érdemes azt is megfigyelnünk, hogy 13 meccs esetén a biztos 12 találat eléréséhez 59 049 tippre van szükségünk, ami jelenleg 2 361 960 Ft-ba kerül. Ezt összehasonlítva a korábban említett nyereménnyel (4 440 Ft), látható hogy sajnos a TOTÓ-val sem lehet biztosan meggazdagodni.
A most következő példában és esetén adjuk meg az egyik optimális konstrukciót, ami a harmadrendű véges affin sík tulajdonságait használja. A véges affin síkokról részletesen olvashatunk a lapunk 2006. decemberi számában megjelent [3] cikkben, vagy a [4] könyvben. Most csak a továbbiakban -val jelölt harmadrendű affin sík legfontosabb tulajdonságait foglaljuk össze.
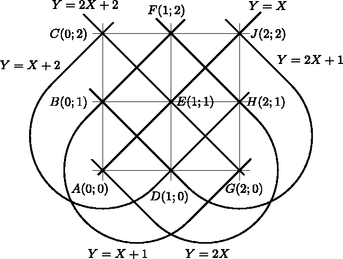
-t legegyszerűbben egy derékszögű koordináta-rendszerrel ellátott klasszikus euklidészi sík mintájára képzelhetjük el, csak most a valós számok helyett a halmaz elemeivel koordinátázunk és modulo 3 számolunk. Legyenek pontjai az olyan rendezett párok, ahol (a klasszikus esetben a sík pontjai a valós számokból készített rendezett pároknak felelnek meg). Az egyenesek kétfélék: egyrészt az típusú rendezett párok, ahol , másrészt a típusú elemek, ahol (a klasszikus esetben a sík nem függőleges egyenesei egyértelműen megadhatók meredekségükkel és azzal a ponttal, ahol az tengelyt metszik, míg a függőleges egyenesek egyértelműen leírhatók azzal a ponttal, ahol az tengelyt metszik). Két egyenesre azt mondjuk, hogy párhuzamosak, ha mindkettő típusú, vagy ha mindkettő típusú és a két egyeneshez tartozó értékek megegyeznek. Az pont akkor és csak akkor van rajta az egyenesen, ha teljesül, hogy (azaz az szám 3-mal osztva -t ad maradékul), a egyenesen pedig pontosan akkor, ha . A klasszikus esethez hasonlóan azt mondjuk, hogy az egyenes egyenlete , illetve a egyenes egyenlete . A síkon tehát pont és egyenes van. Az ábrán pontjai koordinátáikkal, egyenesei pedig (amik persze az ábrán nem rajzolhatók meg úgy, mint az euklidészi sík egyenesei) egyenletükkel együtt szerepelnek.
Az ábra alapján is könnyen ellenőrizhetjük, hogy rendelkezik a következő tulajdonságokkal:
| Bármely két különböző pontnak egyértelműen létezik összekötő egyenese. |
| minden egyenesén pont van és minden ponton át egyenes megy. |
| Ha a sík pontja nincs rajta a sík egyenesén, akkor -n át pontosan egy -vel párhuzamos egyenes megy. A sík egyenesei párhuzamossági osztályokba sorolhatók úgy, hogy két egyenes pontosan akkor van egy osztályban, ha párhuzamosak. Minden osztályban darab egyenes van, a sík minden pontján át minden osztályból pontosan egy egyenes megy. |
A tippeket a sík pontjainak feleltetjük meg. Minden ponthoz hozzárendelünk egy négy hosszú vektort, melynek minden koordinátája 0, 1 vagy 2, a következő módon: Tekintsük a sík -n átmenő négy egyenesét. Ezek közül pontosan egy-egy tartozik a sík mind a négy párhuzamossági osztályába. Ha az egyenesek egyenlete rendre akkor a -hez rendelt vektor legyen (Tehát az ábrán látható ponthoz a vektort rendeljük, mert a -n átmenő egyenesek egyenletei , , és .)
Ha és a sík két különböző pontja, akkor a hozzájuk rendelt két vektornak, -nek és -nak pontosan egy koordinátája egyezik meg, hiszen a síkon a két pontnak egyértelműen létezik összekötő egyenese. Vagyis a két vektor Hamming-távolsága . Ez viszont azt jelenti, hogy ha a sík pontjaihoz rendelt vektorok köré 1 sugarú gömböket írunk, akkor azoknak nem lesz közös pontjuk. Ha ugyanis ilyen lenne, akkor a háromszög-egyenlőtlenséget alkalmazva a | |
nyilvánvaló ellentmondást kapnánk.
Minden gömb vektort tartalmaz, tehát a sík 9 pontjához tartozó gömbök összesen vektort, vagyis az halmaz minden elemét tartalmazzák. Ezért a 4 meccsből álló TOTÓ-ban biztos 3 találatot érhetünk el az alábbi tippsorozattal (a vektorokat a harmadrendű sík pontjaihoz az ábrán látható jelöléseknek megfelelően rendeltük): | |
Feladatok
1. Adjunk meg esetén 3 tippet, melyekkel biztos 1 találatot érünk el. Mutassuk meg, hogy 2 tipp esetén előfordulhat, hogy 0 találatunk lesz.
2. Adjunk meg esetén 3 tippet, melyekkel biztos 2 találatot érünk el. (Gondoljunk arra, hogyan kell 13 meccs esetén biztos 5 találatot csinálni.)
3. Az esetben, ha biztos 2 találatot szeretnénk elérni, akkor a gömbpakolási korlátból azt kapjuk, hogy ehhez legalább 4 tippre van szükségünk (mert ). Mutassuk meg, hogy ekkor a gömbpakolási korlát nem éles, azaz legalább 5 tippre van szükségünk a biztos 2 találat eléréséhez.
4. Adjunk meg 27 tippet, amelyekkel biztos 4 találatot érünk el az 5 meccset tartalmazó játékban.
5. Bizonyos esetekben a meccsek kétesélyesek (azaz feltételezzük, hogy a három lehetséges eredmény közül az egyik biztosan nem fog bekövetkezni). Ilyenkor 0‐1 sorozatokkal modellezhetjük a tippeket. Hogyan szól darab kétesélyes meccs estén a 3. tételben szereplő gömbpakolási korlát megfelelője? Adjunk meg olyan 16 elemű tipphalmazt a 7 kétesélyes meccsből álló játékban, amellyel biztos 6 találatot érünk el.
Irodalomjegyzék
| [1] | Hämäläinen, H., Honkala, I., Lytsin, S. és Östergrd, P.: Football Pools ‐ A Game for Mathematicians, American Math. Monthly (August‐Sept. 1995), 579‐588. |
| [2] | Hraskó A. és Szőnyi T.: Hibajavító kódok, Új matematikai mozaik (szerk. Hraskó A.), Typotex Kiadó (Budapest, 2002), 139‐170. |
| [3] | Kiss Gy.: Hogyan szervezzünk körmérkőzéses focibajnokságot? KöMaL, 56 (2006), 514‐525. |
| [4] | Kiss Gy. és Szőnyi T.: Véges geometriák, Polygon Könyvkiadó (Szeged, 2001). |
|
PDF | MathML 