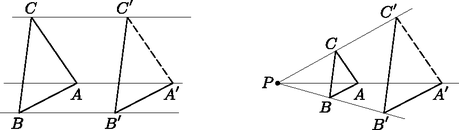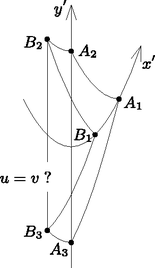Kezdőlap


Cím:	Egy érdekes és egyszerű transzformációval származtatott nem-desargues-i affin sík
Szerző(k):	Korchmáros Gábor , Szőnyi Tamás
Füzet:	2007/május, 258 - 266. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Száz éve, 1907. február 13-án született Kárteszi Ferenc professzor. Utolsó cikke [3] egyik kedvenc témájával, Desargues tételével foglalkozik. Ehhez kapcsolódik két cikkünk, melyet Kárteszi professzor egykori diákjai írtak szeretett tanáruk születésének centenáriumára emlékezve. Az első cikk ([6]) lapunk márciusi számában jelent meg. A jelen dolgozat szorosan kapcsolódik az említett két cikkhez. Mielőtt a címben jelzett témára rátérnénk, először lássuk, mit is neveznek ma ,,axiomatikus geometriának''.
A geometria axiomatizálása Eukleidésszel kezdődött, s ez az axiómarendszer a XIX. század végéig változatlan maradt. Az axiomatizálás célja az embert körülvevő fizikai tér minél pontosabb absztrakt leírása volt. A geometria egyik központi kérdése az volt, hogy a párhuzamossági axióma levezethető-e a geometria többi euklidészi axiómájából. A XIX. század elején Bolyai és Lobacsevszkij megmutatták, hogy erre a kérdésre a válasz tagadó, felépítették az első nem-euklidészi geometriákat. Munkásságuk nyomán már nem tűnt olyan idegennek az euklidészitől különböző geometriákat elképzelni. Amikor Hilbert 1899-ben megadta az euklidészi geometria axiómarendszerét (l. Reiman [10], 366. old.), az axiómákat öt csoportba osztotta (illeszkedési, rendezési, egybevágósági, folytonossági és párhuzamossági), és megvizsgálta külön-külön is ezek következményeit. Így például csupán az illeszkedési axiómákat tekintve megadhatók olyan, a szemlélettől eltérő objektumok is, amelyek az axiómáknak eleget tesznek. Annak, hogy a XX. század elején az axiómákkal már sok lehetséges geometria közös tulajdonságait próbálták megragadni, Bolyaiék munkásságán túl, másik oka az absztrakt algebra fejlődése volt (itt a tipikus axiómarendszerek kevés axiómából állnak és sok lényegesen különböző nekik eleget tevő struktúra van). Hogy konkrétan is lássunk egy ilyen sok geometriát megengedő axiómarendszert, nézzük az ,,absztrakt affin síkok'' alábbi illeszkedési axiómáit:
A síkot, mint egy $Σ$ ponthalmazt képzeljük el, az egyenesek pedig bizonyos kitüntetett részhalmazok. Ha egy pont eleme egy egyenesnek, azt a ,,pont illeszkedik az egyenesre'' szóhasználattal is kifejezzük.

I_{1}

Két különböző pontra egy és csak egy egyenes illeszkedik.

I_{2}

Egy egyeneshez és egy rajta kívüli ponthoz egy és csak egy olyan egyenes van, amelynek az adott egyenessel nincs közös pontja és az adott pontra illeszkedik.

I_{3}

Van három olyan pont, amely nem illeszkedik egy egyenesre.

I_{2}

axiómában szereplő egyeneseket a szokásos terminológiával párhuzamosnak mondjuk. Az

I_{3}

axióma csupán a teljesen banális struktúrák kizárására szolgál. Axiómáink legegyszerűbb modellje az alábbi: legyen pontjaink halmaza egy 4 elemű halmaz, az egyenesek ennek kételemű részhalmazai. Az Olvasó könnyen ellenőrizheti, hogy az axiómák teljesülnek. További (véges és nem véges) modelleket találhatunk Kárteszi [4], Montágh [9] cikkeiben, valamint a Lovász, Pelikán, Vesztergombi [8] könyvben. Természetesen jogos a félelem, hogy ezek a nagyon egyszerű axiómák túl gyöngék ahhoz, hogy segítségükkel nem-triviális tételeket vezessünk le. Azért, hogy érdekesebb ,,geometriákhoz'' jussunk, kézenfekvő kibővíteni axiómarendszerünket. További axiómaként választhatunk például egy olyan, a klasszikus geometriában megismert tételt, amelynek megfogalmazásához csupán az összekötés, metszés és párhuzamosság szükséges, hiszen ezeket már

I_{1}

és

I_{2}

alapján értelmezhetjük. Hilbert munkái mutatnak rá, hogy a Desargues-tétel (a későbbiekben röviden

D

-tétel) alkalmas erre a célra.

Ha az

A B C

A' B' C'

háromszögek olyanok, hogy az

A A'

B B'

C C'

egyenesek egy közös ponton mennek át, akkor az

A B

A' B'

;

B C

B' C'

;

C A

C' A'

egyenespárok

X

Y

, és

Z

metszéspontjai egy egyenesen vannak.

D

-tétel érdekes sajátossága, hogy belőle könnyen adódik megfordítása is. Érdemes megemlíteni, hogy a

D

-tétel igaz marad akkor is, ha kimondásában az ,,egyenesek egy közös ponton mennek át'' feltételt az ,,egyenesek párhuzamosak'' feltétellel cseréljük fel. Így többek között a

D

-tétel alábbi két fontos speciális esetét fogalmazhatjuk meg, melyeket rendre

D_{0}

-tételnek és

D_{1}

-tételnek nevezünk.

D_{0}

-tétel. Ha az

A B C

és az

A' B' C'

háromszögek úgy helyezkednek el a síkon, hogy az

A A'

B B'

és

C C'

egyenesek párhuzamosak, továbbá az

A B

egyenes párhuzamos az

A' B'

egyenessel, a

B C

egyenes pedig párhuzamos a

B' C'

egyenessel, akkor a

C A

egyenes is párhuzamos a

C' A'

egyenessel.

D_{1}

-tétel. Ha az

A B C

és az

A' B' C'

háromszögek úgy helyezkednek el a síkon, hogy az

A A'

B B'

és

C C'

egyenesek egy közös

P

ponton mennek át, továbbá az

A B

egyenes párhuzamos az

A' B'

egyenessel, a

B C

egyenes pedig párhuzamos a

B' C'

egyenessel, akkor a

C A

egyenes is párhuzamos a

C' A'

egyenessel.

A Desargues-tételről részletesen olvashatunk Kiss György [6] cikkében, valamint Kárteszi [4, 5], Lánczos [7] és Coxeter [1, 2] könyveiben és persze Kárteszi [3] cikkében.
Most már rátérhetünk az egyszerű transzformációval származtatott affin síkunk vizsgálatára. Jelölje

R

a valós számok halmazát,

f

alkalmas

R \to R

függvényt,

f^{*}

pedig az

f

grafikonját, mint ponthalmazt az euklidészi síkon. Definiáljunk új egyeneseket a régi pontok halmazán a következő módon: egyrészt a függőleges egyenesek, másrészt

f^{*}

összes eltoltjai legyenek az új egyenesek. Persze semmi sem garantálja, hogy ilyen módon affin síkot kapunk. Arra a kérdésre, hogy ilyen módon mikor jutunk affin síkhoz, az alábbi állítás válaszol.

1. tétel. A fenti módon definiált új egyenesek meghatározta sík pontosan akkor affin sík, ha teljesül a következő feltétel:

$S)$	minden nem-függőleges $v$ vektorhoz pontosan egy olyan $(P_{1}, P_{2})$ pontpár van $f^{*}$ -on, amelyre $\vec{P_{1} P_{2}} = v$ .

Bizonyítás. Csak azt látjuk be, hogy ha az

S)

feltétel teljesül, akkor az új egyenesek meghatározta sík affin sík, az itt csak vázlatosan szereplő részek és a másik irány bizonyítását feladatnak hagyjuk.
Az

I_{1}

axióma ellenőrzéséhez legyen

A_{1} \neq A_{2}

a sík két pontja, és

v = \vec{A_{1} A_{2}}

. Ha

v

függőleges,

I_{1}

könnyen ellenőrizhető. Ha nem az, akkor

S)

szerint egyértelműen van olyan

(P_{1}, P_{2})

pontpár

f^{*}

-on, amelyre

\vec{P_{1} P_{2}} = v

. Ha

f^{*}

-ot az

\vec{P_{1} A_{1}}

vektorral eltoljuk, akkor megkapjuk az

A_{1}

A_{2}

pontokat összekötő ,,új egyenest''. Az összekötő egyenes egyértelműsége a

(P_{1}, P_{2})

pontpár egyértelműségéből következik, mivel az eltolás kölcsönösen egyértelmű.
Az

S)

feltétel azt is maga után vonja, hogy ha

f^{*}

-ot egy nem-függőleges

v

vektorral eltoljuk, akkor ez az eltolt metszi

f^{*}

-ot, mégpedig azon

P_{2}

pontban, amelynek létezését az

S)

feltétel garantálja. Ebből az következik, hogy két ,,új egyenes'' akkor és csak akkor párhuzamos az új síkon, ha egymásból függőleges eltolással kapható.
Az

I_{3}

axióma ellenőrzése nagyon egyszerű: legyen

A_{1}

és

A_{2}

két különböző pont az

f^{*}

,,új egyenesen'',

A_{3}

pedig legyen az

A_{1}

-en átmenő függőleges egyenes egy

A_{1}

-től kölönböző pontja. Ekkor az

A_{1}

A_{2}

A_{3}

ponthármas nincs egy egyenesen.

□

Persze most az a kérdés, hogy vannak-e egyáltalán az

S)

feltételnek eleget tevő függvények. A [3] dolgozat egyik eredménye szerint például a normálparabola (az

f : x \mapsto x^{2}

grafikonja) ilyen. A kérdés megválaszolásához lássuk az

S)

feltétel algebrai megfogalmazását.

2. tétel. Az

f

függvény grafikonjára akkor és csak akkor teljesül az

S)

feltétel, ha minden

a \neq 0

valós számra a

\begin{matrix} g : R \to R, x \mapsto g (x) = f (x + a) - f (x) \end{matrix}

valós függvény kölcsönösen egyértelmű.

Bizonyítás (vázlat). A feltétel azt mondja, hogy minden

a \neq 0

-ra és minden

b

-re az

f (x + a) - f (x) = b

egyenletnek pontosan egy

x_{0}

megoldása van. Ez a

v = (a, b)

vektorra biztosítja az

S)

feltétel teljesülését:

P_{1}

x_{0}

P_{2}

pedig az

x_{0} + a

abszcisszájú pont az

f^{*}

grafikonon. A részletes bizonyítást feladatnak hagyjuk.

□

A 2. tételből azonnal következik, hogy az

f (x) = x^{2}

függvényre teljesül az

S)

feltétel, hiszen ebben az esetben

f (x + a) - f (x) = 2 a x + a^{2}

lineáris függvény, így

a \neq 0

esetén kölcsönösen egyértelmű.
Lássuk ugyanennek egy szemléletes bizonyítását is. Keressük meg az

f^{*}

normálparabola egy olyan érintőjét, amely párhuzamos

v

-vel. Ez az érintő (igazi egyenes) teljesen

f^{*}

alatt marad. Kezdjük el ezt az egyenest önmagával párhuzamosan felfelé mozgatni. Ezek az egyenesek a normálparabolát két pontban metszik. Az elmozgatáskor ennek a két metszéspontnak a távolsága szigorúan monoton nő és folytonosan változik, így pontosan egy olyan helyzet lesz, amikor a két metszéspont távolsága éppen

v

hossza lesz. Ekkor az

S)

feltételben szereplő

P_{1}

P_{2}

pontok ezen metszéspontok lesznek (az egyik sorrend esetén a

v

, a másik sorrend esetén a

- v

vektorhoz tartoznak).
Ez a szemléletes okoskodás azt is mutatja, hogy meglehetősen sok olyan függvény van, amely eleget tesz az

S)

feltételnek. A rövidség kedvéért az

S)

feltételt kielégítő függvényeket planáris függvényeknek fogjuk nevezni. A következő tétel szemléletes tartalma az, hogy ha egy függvény grafikonja ,,hasonlít'' a parabolához, akkor az planáris.

3. tétel. Ha egy

f

függvény alulról szigorúan konvex, továbbá

\begin{matrix} {lim}_{- \infty}^{} \frac{f (x)}{x} = - \infty, {lim}_{+ \infty}^{} \frac{f (x)}{x} = + \infty, \end{matrix}

akkor a függvény planáris.

A szigorúan szó itt azt jelenti, hogy

f

grafikonja nem tartalmazhat egyenes szakaszt. Az előző szemléletes bizonyítás ilyen függvényekre szinte szó szerint lemásolható, érintő helyett

v

-vel párhuzamos támaszegyenest keresünk. A határértékekre vonatkozó feltételek azt biztosítják, hogy akármilyen meredek támaszegyenes létezzék, a konvexitás pedig azt, hogy a támaszegyenes elmozgatása során két metszéspont legyen, amelyek távolsága szigorúan monoton nő és folytonos módon változik. A 2. tételre is hivatkozhatnánk, a konvexitás azt jelenti, hogy az itteni

g

függvény

a > 0

-ra szigorúan monoton növő,

a < 0

-ra pedig szigorúan monoton csökkenő. A határértékekre vonatkozó feltételek azt garantálják, hogy

g

értékkészlete a teljes

R

legyen.
Azt sem lenne túl nehéz megmutatni, hogy a folytonos függvények között éppen a 3. tétel feltételeit teljesítő függvények és ezek ellentettjei lesznek planárisak, ezt feladatnak hagyjuk. Persze ennek a feladatnak a megoldásához szükség van a konvex függvényekkel kapcsolatos ismeretekre.

Jelölés. Ha

f

planáris függvény, akkor a belőle a fent leírt eljárással kapott új síkot

I (f)

-fel jelöljük.

Kárteszi tanár úr [3] dolgozatában a fő kérdés az volt, hogy új síkunkon mikor teljesül Desargues tétele. Régi és új síkunk között alkalmas transzformációt keresve, amely a régi egyeneseket ,,elgörbíti'', megmutatható az alábbi fontos tétel:

4. tétel. Ha

f

másodfokú függvény, akkor

I (f)

izomorf az euklidészi síkkal.

Ebben a tételben az izomorf szó azt jelenti, hogy a régi és új sík pontjai között megadható olyan kölcsönösen egyértelmű megfeleltetés, amely a régi egyeneseket éppen az új egyenesekbe viszi.
Mi most csupán arra szeretnénk példát mutatni, hogy planáris függvények segítségével elég egyszerűen adhatunk meg olyan affin síkot, amelyen a

D

-tétel nem teljesül. A dolgozat végén egy feladatsort találunk, amely planáris függvények és az általuk származtatott síkok további tulajdonságaira mutat rá.
Hogy a szokásos kooordináta-geometriához hasonlóan számolhassunk az

I (f)

affin síkon is, Kárteszi [3] dolgozatához hasonlóan vezessünk be egy kölcsönösen egyértelmű pont-transzformációt. Jelöljük a szokásos módon az eredeti euklidészi sík koordinátáit

x

-szel és

y

-nal. Ekkor az új egyenesek

f^{*}

-ból a

(- a, B)

vektorral való eltolással kaphatók, így egyenletük ebben a koordináta-rendszerben

\begin{matrix} x = c vagy y = f (x + a) + B \end{matrix}

alakú (

c

, illetve

a

és

B

állandók). Írjuk át

f (x + a)

-t a következőképpen:

\begin{matrix} f (x + a) = f (x) + g (x, a) + f (a) . \end{matrix}

Ez a felírás, legalábbis akkor, ha

f

polinom, a binomiális tétel miatt kézenfekvő. A 2. tétel miatt is hasznos olyan kifejezést bevezetni, ami tartalmazza az

f (x + a) - f (x)

különbséget, hiszen erről tudjuk, hogy kölcsönösen egyértelmű. Ezzel a

g

függvénnyel

f^{*}

eltoltjainak egyenlete

\begin{matrix} y = f (x + a) + B = f (x) + g (x, a) + (f (a) + B) \end{matrix}

alakú lesz. Vezessük be az

\begin{matrix} x' & = & x, \\ y' & = & y - f (x) \end{matrix}

új koordinátákat. Így az új egyenesek egyenlete

x'

y'

felhasználásával

\begin{matrix} x' = c, vagy y' = g (x', a) + b \end{matrix}

alakban írható. Ha

f (x) = x^{2}

, akkor ez a pont-transzformáció megegyezik a Kárteszi [3] dolgozatában található transzformációval. Ebben az esetben

\begin{matrix} {(x + a)}^{2} = x^{2} + 2 x a + a^{2}, vagyis g (x, a) = 2 x a . \end{matrix}

Ez lényegében a valós számok szorzása, kicsit elügyetlenkedve. Ha most az általános esetben is bevezetünk egy új ,,szorzást'' az

u * a = g (u, a)

definícióval, akkor az egyenesek egyenlete kísértetiesen emlékeztet az egyenes szokásos egyenletére. Persze ez csak formális hasonlóság abban az értelemben, hogy ez a szorzás általában sokkal kevesebbet teljesít a megszokott műveleti tulajdonságok közül (például általában nem asszociatív). Húzzuk alá még egyszer, hogy

u * a = f (u + a) - f (u) - f (a)

. Ez a felírás mutatja, hogy

*

kommutatív. Az új szorzást mi lényegében arra fogjuk használni, hogy az

I (f)

síkon a koordinátákkal végzett számolásaink jobban hasonlítsanak a szokásos koordinátákkal való számolásokhoz.
A továbbiakban csak a legegyszerűbb ilyen függvényekkel, az

y = x^{2 k}

alakú általánosított parabolákkal foglalkozunk. Ekkor

\begin{matrix} a * b = {(a + b)}^{2 k} - a^{2 k} - b^{2 k} = \sum_{i = 1}^{2 k - 1} (\binom{2 k}{i}) a^{2 k - i} b^{i} . \end{matrix}

Az, hogy ezek a függvények planárisak, abból következik, hogy grafikonjuk nagyon hasonlít a parabolára (v.ö. 3. tétel). A

k = 2

speciális eset egy kicsit még egyszerűbb, ekkor csak másodfokú egyenletekre vezető egyenletrendszerek fordulnak elő. Vizsgáljuk meg, vajon a

D_{0}

-tétel teljesül-e új síkunkon. Próbáljunk meg felépíteni egy a

D_{0}

-tételben látható ábrát. Válasszunk az új síkon három párhuzamos egyenest, azaz például az eredeti

f^{*}

három függőleges eltoltját. Az

x'

y'

koordinátákban ezek egyenlete a vízszintes egyenesekére emlékeztet. A háromszögek megfelelő oldalainak párhuzamosaknak kell lenniük, legyen egy oldalpár függőleges, a másik kettő meredeksége pedig legyen

+ 1

és

- 1

. Ez pontosan azt jelenti, hogy az oldalak egyenlete rendre

\begin{matrix} x' = c, y' = x * 1 + ..., y' = x * (- 1) + ... \end{matrix}

alakú. Legyen az

A_{1}

csúcs az

y' = 0

vízszintes egyenesen, mondjuk legyen

A_{1}

(1; 0)

pont (új koordinátákban). Mivel az

A_{1} A_{2} A_{3}

háromszög

A_{1} A_{3}

és

A_{1} A_{2}

oldalainak meredeksége

+ 1

és

- 1

, így az oldalak egyenlete rendre:

\begin{matrix} y' = x' * 1 + b_{1}, y' = x' * (- 1) + b_{2}, \end{matrix}

ahol a

b_{1}

b_{2}

számok abból a feltevésből határozhatók meg, hogy az

A_{1}

pont rajta legyen az egyeneseken. Így

b_{1} = - (1 * 1)

, míg

\begin{matrix} b_{2} = - (1 * (- 1)) = - ({(1 - 1)}^{2 k} - 1 - 1) = 2. \end{matrix}

Eszerint

A_{2}

(0; 2)

A_{3}

pedig a

(0; - (1 * 1))

pont, hiszen azt akarjuk, hogy az

A_{2} A_{3}

egyenes függőleges legyen. Hasonló módon legyen

B_{1}

is az

y' = 0

egyenletű új egyenesen, legyen mondjuk

B_{1}

(\frac{1}{2}; 0)

pont (új koordinátákban). A

B_{2}

B_{3}

pontokat úgy kell felvenni, hogy

B_{1} B_{2}

meredeksége

+ 1

, míg

B_{1} B_{3}

meredeksége

- 1

legyen, továbbá, hogy az

A_{2} B_{2}

és

A_{3} B_{3}

egyenesek vízszintesek legyenek, vagyis egyenletük

y' = c

alakú legyen. Eszerint

B_{2}

nem más, mint az

y' = 2

és

y' = x' * (- 1) + 1

B_{3}

pedig az

y' = - (1 * 1)

és

y' = x' * 1 - (1 * (\frac{1}{2}))

egyenesek metszéspontja. Ugyanúgy, mint

A_{2}

és

A_{3}

meghatározásánál, a ferde egyenesek egyenletében szereplő konstansokat itt is úgy határoztuk meg, hogy az

x' = \frac{1}{2}

y' = 0

érték kielégítse az egyenleteket, azaz

B_{1}

rajta legyen az egyeneseken. Ennek alapján

B_{2}

koordinátái

(u; 2)

B_{3}

-é pedig

(v; - (1 * 1))

, alkalmas

u

v

számokkal. Most már lényegében készen áll a

D_{0}

-tételben szereplő konfiguráció, a háromszögek megfelelő csúcsait összekötő egyenesek egymással párhuzamosak, valamint a háromszögek megfelelő oldalai legfeljebb a

B_{2} B_{3}

és

A_{2} A_{3}

oldalpár kivételével szintén párhuzamosak. Ha új síkunkon teljesül a

D_{0}

-tétel, akkor

B_{2} B_{3}

és

A_{2} A_{3}

is párhuzamos kell legyen. Ez a

B_{2}

és

B_{3}

pontok koordinátáira pontosan azt jelenti, hogy

u = v

Behelyettesítve

B_{2}

, illetve

B_{3}

koordinátáit a

B_{1} B_{2}

és

B_{1} B_{3}

egyenesek egyenletébe az alábbi egyenleteket kapjuk:

\begin{matrix} u * (- 1) = 1, u * 1 = - (1 * 1) + (1 * (\frac{1}{2})) . \end{matrix}

Beírva a

*

művelet definícióját, ez azt jelenti, hogy

\begin{matrix} \sum_{i = 1}^{2 k - 1} (\binom{2 k}{i}) u^{2 k - i} {(- 1)}^{i} = 1, \\ \sum_{i = 1}^{2 k - 1} (\binom{2 k}{i}) u^{2 k - i} = - 2^{2 k} + 2 + {(\frac{3}{2})}^{2 k} - {(\frac{1}{2})}^{2 k} - 1. \end{matrix}

Összeadva a két egyenletet, a páratlan kitevős tagok kiesnek:

\begin{matrix} 2 \cdot \sum_{i = 1}^{k - 1} (\binom{2 k}{2 i}) u^{2 k - 2 i} = - 2^{2 k} + {(\frac{3}{2})}^{2 k} - {(\frac{1}{2})}^{2 k} + 2, \end{matrix}

ami viszont lehetetlen, mert a bal oldal pozitív, míg a jobb oldal negatív. Ez tehát azt jelenti, hogy a felrajzolt esetben

B_{2} B_{3}

nem függőleges, azaz a

D_{0}

-tétel nem teljesül általában.
Érdemes külön kiemelni, hogy a

k = 2

esetben, azaz az

f : x \mapsto x^{4}

választásnál a binomiális tétel helyett az összeg négyzetreemeléséről szóló azonosság kétszeri alkalmazása is megteszi, s ebben az esetben a végső ellentmondás is egy másodfokú egyenlet megoldhatatlansága. Ebben az

f (x) = x^{4}

esetben a

D_{1}

-tétel érvényességét is megvizsgálhatjuk az említett egyszerű módon. Igazából itt a

D_{1}

-tétel megfordítását ellenőrizzük, de mint azt a Desargues-tételnél említettük, a

D

-tételből annak megfordítása is következik. Ez mindkét általunk használt speciális esetre is így van, ennek meggondolását feladatnak hagyjuk. A

D_{1}

-tétel nem-teljesülését sokkal kevésbé részletesen tárgyaljuk, mint az előző esetben. Könnyen látható, hogy az

\begin{matrix} A_{1} (0; - 1); A_{2} (\frac{1}{2}; - 1); A_{3} (\frac{1}{2}; 3) \end{matrix}

és

\begin{matrix} B_{1} (0; - 2); B_{2} (1; - 2); B_{3} (1; 12) \end{matrix}

háromszögek (ahol

12 = 1 * 1 - 2 = {(1 + 1)}^{4} - 1 - 1 - 2

) a

D_{1}

-tételben szereplő konfigurációt alkotnak, melyben a

D_{1}

-tételbeli

P

pont csak az origó lehet. Így a

D_{1}

-tétel pontosan akkor teljesül, ha az origó, az

A_{3}

és a

B_{3}

pontok kollineárisak, azaz ha van olyan

a

szám, amelyre

A_{3} B_{3}

egyenlete

y' = x' * a

alakú, vagyis, ha

\begin{matrix} a * (\frac{1}{2}) = 3 és a * 1 = 12 \end{matrix}

egyszerre teljesül. Beírva a

*

művelet definícióját azt kapjuk, hogy

\begin{matrix} 4 a^{3} + 6 a^{2} + 4 a & = & 12, \\ 2 a^{3} + \frac{3 a^{2}}{2} + \frac{a}{2} & = & 3. \end{matrix}

A második egyenletet

2

-vel szorozva, majd a két egyenletet kivonva a

\begin{matrix} 3 a^{2} + 3 a - 6 = 0 \end{matrix}

egyenletet kapjuk, amelynek gyökei

1

és

- 2

, a visszahelyettesítés azonban mutatja, hogy ezek az eredeti egyenleteknek nem gyökei. Így síkunkon a

D_{1}

-tétel sem teljesül univerzálisan.
A bemutatott példák is mutatják, hogy planáris függvény segítségével származtatott síkon tipikusan még a

D_{0}

-tétel sem teljesül. A most következő feladatsorozat megoldói azt láthatják be, hogy a folytonos planáris függvények közül pontosan a parabolák azok, amelyekből származtatott síkon a

D_{0}

-tétel teljesül. A feladatsor lényegében a [11] dolgozatot követi.

1. feladat. Legyen

f

tetszőleges valós függvény. Új síkunk egyenesei a függőleges egyenesek mellett legyenek az

y = f (x) + a x + b

grafikonok, az összes

a

b

-re. Mutassuk meg, hogy ez az eljárás mindig az eredeti euklidészi síkkal izomorf síkot ad.

2. feladat. Mutassuk meg, hogy a

D

-tételből annak megfordítása is következik, sőt ugyanez igaz a

D_{0}

- és a

D_{1}

-tételre is.

3. feladat. Bizonyítsuk be az 1. tétel nem bizonyított részeit.

4. feladat. Részletesen gondoljuk meg a 2. tétel bizonyítását. Ezt felhasználva adjunk bizonyítást arra, hogy az

x \mapsto x^{4}

, illetve általában az

x \mapsto x^{2 n}

függvények planárisak.

5. feladat. Mutassuk meg, hogy ha egy folytonos valós

f

függvény planáris, akkor

f

(vagy

- f

) olyan szigorúan konvex függvény kell legyen, amelyre teljesülnek a 3. tétel feltételei.

A továbbiakban tegyük fel, hogy

f

olyan szigorúan konvex függvény, amelyre teljesülnek a 3. tétel feltételei.

6. feladat. Mutassuk meg, hogy a bevezetett

*

műveletre igaz, hogy bármely

a \neq b

-re és tetszőleges

c

-re pontosan egy olyan

x

van, amelyre

a * x - b * x = c

teljesül.

7. feladat. Az

f (x) = x^{4}

esetre adott bizonyítást lemásolva mutassuk meg, hogy minden

A

B

-re és

j

-re van olyan

u

, amelyre teljesül, hogy

\begin{matrix} f (u + j) + f (u - j) - 2 f (u) + (f (A + j) + f (A - j) - 2 f (A)) = \\ = (f (B + j) + f (B - j) - 2 f (B)) + (f (j) + f (- j) - 2 f (0)) . \end{matrix}

A feladat megoldásában

A

B

A_{1}

B_{1}

pontok

x'

-koordinátáját jelöli, a korábbi bizonyításban szereplő

+ 1

- 1

meredekségek szerepét itt a

+ j

- j

veszi át.

8. feladat. Mutassuk meg, hogy ha az

f

függvény nem deriválható, akkor az

I (f)

affin síkon nem teljesülhet univerzálisan a

D_{0}

-tétel.

9. feladat. Definiáljuk a

d_{j}

függvényt a

\begin{matrix} d_{j} (x) = f (x + j) + f (x - j) - 2 f (x) \end{matrix}

képlettel. Mutassuk meg, hogy a

d_{j}

függvény állandó, azaz van olyan

D_{j}

, amelyre

d_{j} (x) = D_{j}

minden

x

-re.

10. feladat. Mutassuk meg, hogy ha az

f

függvényre

d_{j} (x) = D_{j}

, akkor

f

másodfokú függvény.

Végezetül jegyezzük meg, hogy az eredeti euklidészi sík eltolásai illeszkedéstartó leképezések (kollineációk)

I (f)

-en, amelyekkel minden pontot minden más pontba el tudunk vinni, ezek a kollineációk azonban nem eltolások az

I (f)

síkon (kivéve azokat, amelyek függőleges irányúak). Affin sík egy kollineációja eltolás, ha nincs fixpontja és minden egyenes párhuzamos a képével. Mivel az eredeti sík függőleges eltolásai eltolások maradnak

I (f)

-en, így

I (f)

-en a

D_{0}

-tétel teljesül, ha a két háromszög egymásnak megfelelő csúcsait összekötő egyenesek (az

A A'

B B'

és

C C'

egyenesek) függőlegesek. Ezt a [6]-ban szereplő bizonyítást lemásolva láthatjuk.

A jelen dolgozat első változata közel húsz éve keletkezett. Ekkor Lovász László, Szász Gábor és Wettl Ferenc fűzött hozzá értékes megjegyzéseket. Az új változattal kapcsolatban Ambrus András, Hermann Péter, Kiss György, Károlyi Gyula tett részletes módosítási javaslatokat. Mindannyiuk segítségét nagyon köszönjük.

Irodalom

[1]	Coxeter, H. S. M.: A geometriák alapjai, Műszaki Könyvkiadó (Budapest, 1973).

[2]	Coxeter, H. S. M.: Projektív geometria, Gondolat Kiadó (Budapest, 1986).

[3]	Kárteszi Ferenc: Egy érdekes és egyszerű transzformációval származtatott affin sík, KöMaL, 57 (1978. november), 97‐103.

[4]	Kárteszi Ferenc: Bevezetés a véges geometriákba, Akadémiai Kiadó (Budapest, 1973).

[5]	Kárteszi Ferenc: Lineáris transzformációk, Tankönyvkiadó (Budapest, 1976).

[6]	Kiss György: Desargues tétele, KöMaL, 57 (2007. március), 130‐137.

[7]	Lánczos Kornél: A geometriai térfogalom fejlődése, Gondolat Kiadó (Budapest, 1976).

[8]	Lovász László, Pelikán József, Vesztergombi Katalin: Diszkrét matematika, Typotex Kiadó (Budapest, 2006).

[9]	Montágh Balázs: Salakmotor-versenyek és véges affin síkok, Új matematikai mozaik (szerk.: Hraskó András), Typotex Kiadó (Budapest, 2002).

[10]	Reiman István: A geometria és határterületei, Műszaki Könyvkiadó (Budapest, 1986).

[11]	Szőnyi Tamás: Note on planar functions over the reals, Note di Matematica (Lecce), 10 (1990), 59‐65.