Kezdőlap


Cím:	A 40. Nemzetközi Fizikai Diákolimpia elméleti feladatai
Füzet:	2009/október, 425 - 435. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. A Föld‐Hold rendszer fejlődése^{$^{*}$}

A tudósok nagy pontossággal meg tudják határozni a Föld‐Hold távolságot. Ezt úgy végzik el, hogy űrhajósok által 1969-ben a Holdra helyezett speciális tükörre lőtt lézersugár visszaverődési idejét mérik (hátsó belső borító, bal felső ábra).
Ilyen módszerrel közvetlenül megmutatható, hogy a Hold lassan távolodik a Földtől, azaz a Föld‐Hold távolság időben lassan növekszik. Ennek oka az, hogy az árapály jelenség során a Föld forgatónyomatékkal hat a Holdra, és így (pálya-) impulzusmomentumát (perdületét) megváltoztatja (1. ábra). Ebben a feladatban ennek a jelenségnek a legfontosabb paramétereit vizsgáljuk meg.

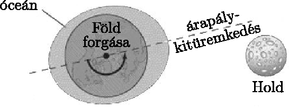1. ábra. A Hold gravitációs hatása következtében a Föld vízfelszínén árapály deformációk, kitüremkedések (,,bulges'') jönnek létre. A Föld forgása miatt a kitüremkedések tengelye nem esik pontosan egybe a Föld‐Hold egyenessel. Ez a kis eltérés olyan forgatónyomatékot eredményez, mely a Föld forgásának impulzusmomentumát csökkenti, a Hold pálya menti impulzusmomentumát pedig növeli. Az ábra nem méretarányos

1. Impulzusmomentum-megmaradás
Legyen

L_{1}

a Föld‐Hold rendszer jelenlegi impulzusmomentuma. Éljünk a következő közelítő feltevésekkel:

i)

L_{1}

csupán a Földnek a tengely körüli forgásából adódó impulzusmomentumának és a Holdnak a Föld körüli keringéséből adódó (pálya-)impulzusmomentumának összege.

i i)

A Hold pályája köralakú, és a Hold pontszerűnek tekinthető.

i i i)

A Föld forgástengelye és a Hold keringésének tengelye párhuzamos.

i v)

A számolás egyszerűsítése érdekében úgy tekintjük, hogy a mozgás a Föld középpontja körül megy végbe, nem pedig a rendszer tömegközéppontja körül. Ebben a feladatban mindenütt minden tehetetlenségi nyomatékot, impulzusmomentumot illetve forgatónyomatékot a Föld tengelyére vonatkoztatunk.

v)

A Nap hatását elhanyagoljuk.
1.a. Add meg a Föld‐Hold rendszer jelenlegi teljes impulzusmomentumát! Válaszodat a következő mennyiségekkel fejezd ki: a Föld tehetetlenségi nyomatéka:

I_{F}

; a Föld forgásának jelenlegi szögsebessége:

ω_{F1}

; a Hold jelenlegi tehetetlenségi nyomatéka a Föld tengelyére vonatkoztatva:

I_{H1}

; a Hold keringésének jelenlegi szögsebessége:

ω_{H1}

.
Ez az impulzusmomentum-átadási folyamat addig tart, amíg a Föld forgásának periódusideje egyenlővé nem válik a Hold Föld körüli keringésének idejével. Ekkor a Hold által az óceánok felszínén okozott árapály kitüremkedések (,,bulges'') tengelye egybe fog esni a Föld‐Hold egyenessel, és a két égitest közti forgatónyomaték nullává válik.
1.b. Add meg a Föld‐Hold rendszer teljes

L_{2}

impulzusmomentumát ebben a végső helyzetben! Ugyanazokkal az egyszerűsítő feltevésekkel dolgozz, mint az 1.a. feladatban. Végeredményedet a következő mennyiségekkel fejezd ki: a Föld tehetetlenségi nyomatéka:

I_{F}

; a Föld forgásának és a Hold keringésének végső szögsebessége:

ω_{2}

; a Hold végső tehetetlenségi nyomatéka:

I_{H2}

.
1.c. A végső teljes impulzusmomentumban a Föld forgásának járulékát elhanyagolva írd föl az impulzusmomentum-megmaradás egyenletét erre a problémára!

2. Végső pályasugár és végső szögsebesség a Föld‐Hold rendszerben
Tegyük föl, hogy a Holdat a gravitációs erő minden esetben a Föld körüli körpályán tartja. A végső, teljes impulzusmomentumban a Föld forgásának járulékát hanyagoljuk el.
2.a. A végső helyzetben írd föl a Föld körül keringő Holdra a körmozgás alapegyenletét a következő mennyiségek felhasználásával:

M_{F}

ω_{2}

G

és

D_{2}

, ahol

D_{2}

a végső távolság a Föld és a Hold között,

M_{F}

a Föld tömege,

G

pedig a gravitációs állandó.
2.b. Add meg a Hold végső pályasugarát,

D_{2}

-t a következő mennyiségekkel: a rendszer teljes impulzusmomentuma:

L_{1}

; a Föld, illetve a Hold tömege:

M_{F}

, illetve

M_{H}

; a gravitációs állandó

G

.
2.c. Add meg a Föld‐Hold rendszer végső

ω_{2}

szögsebességének képletét az

L_{1}

M_{F}

M_{H}

és

G

mennyiségek segítségével!
Most

D_{2}

és

ω_{2}

számszerű értékét határozzuk meg. Ehhez szükség van a Föld tehetetlenségi nyomatékára.
2.d. Tételezzük föl, hogy a Föld sűrűsége belül, a középponttól

r_{1}

sugárig

ϱ_{1}

, míg ezen kívül, tehát az

r_{1}

sugártól a felszínig,

r_{0}

-ig a sűrűség

ϱ_{0}

. Add meg a Föld

I_{F}

tehetetlenségi nyomatékának képletét (2. ábra)!

2. ábra. A gömb alakú Föld a két különböző,

ϱ_{1}

és

ϱ_{0}

sűrűségű tartománnyal

Ebben a feladatban a kért számadatokat minden esetben két értékes jegy pontossággal határozd meg!
2.e. Határozd meg a Föld

I_{F}

tehetetlenségi nyomatékának számértékét, felhasználva, hogy

ϱ_{1} = 1, 3 \cdot 10^{4} {kg m}^{- 3}

r_{1} = 3, 5 \cdot 10^{6}

ϱ_{0} = 4, 0 \cdot 10^{3} {kg m}^{- 3}

és

r_{0} = 6, 4 \cdot 10^{6}

m.
A Föld, illetve a Hold tömege

M_{F} = 6, 0 \cdot 10^{24}

kg, illetve

M_{H} = 7, 3 \cdot 10^{22}

kg. A két égitest jelenlegi távolsága

D_{1} = 3, 8 \cdot 10^{8}

m. A Föld forgásának jelenlegi szögsebessége

ω_{F1} = 7, 3 \cdot 10^{- 5} s^{- 1}

. A Hold Föld körüli keringésének jelenlegi szögsebessége

ω_{H1} = 2, 7 \cdot 10^{- 6} s^{- 1}

, a gravitációs állandó értéke pedig

G = 6, 7 \cdot 10^{- 11} m^{3} {kg}^{- 1} s^{- 2}

.
2.f. Határozd meg a rendszer

L_{1}

teljes impulzusmomentumának számértékét!
2.g. Határozd meg a végső,

D_{2}

pályasugár értékét méterben, valamint a jelenlegi,

D_{1}

pályasugár arányában!
2.h. Határozd meg a végső,

ω_{2}

szögsebesség értékét s

^{- 1}

-ban, valamint add meg a végső helyzetben egy nap hosszát a jelenlegi nap hosszának arányában!
Ellenőrizd, hogy a végső, teljes impulzusmomentumban a Föld forgásából adódó járulék valóban elhanyagolható! Ehhez azt kell megmutatni, hogy a Föld és a Hold végső impulzusmomentumának aránya kis szám.
2.i. Határozd meg a végső helyzetben a Föld és a Hold impulzusmomentumának arányát!

3. Mennyivel távolodik a Hold évenként?
Ebben a részben azt határozzuk meg, hogy mennyivel távolodik a Hold a Földtől évenként. Ehhez először ki kell számolni, hogy jelenleg mekkora forgatónyomatékot fejt ki a Föld a Holdra. Tegyük fel, hogy az árapály deformációból származó kitüremkedések két

m

tömegű tömegponttal közelíthetőek, melyek a Föld felszínén helyezkednek el (3. ábra). Legyen továbbá

ϑ

a Föld‐Hold egyenesnek a kitüremkedések tengelyével bezárt szöge.

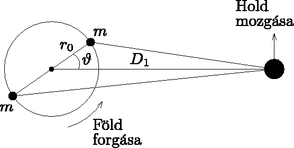3. ábra. Vázlat a dagály-kitüremkedések által a Holdra kifejtett forgatónyomaték számolásához. Az ábra nem méretarányos

3.a. Add meg a Holdhoz közelebbi tömegpont Holdra ható gravitációs erejének

F_{c}

nagyságát!
3.b. Add meg a Holdtól távolabbi tömegpont Holdra ható gravitációs erejének

F_{f}

nagyságát!
Ezután meghatározhatjuk a tömegpontok forgatónyomatékát.
3.c. Határozd meg a közelebbi tömegpont Holdra ható

τ_{c}

forgatónyomatékának nagyságát!
3.d. Határozd meg a közelebbi tömegpont Holdra ható

τ_{f}

forgatónyomatékának nagyságát!
3.e. Határozd meg a két tömegpont

τ

eredő forgatónyomatékának nagyságát! Mivel

r_{0} ≪ D_{1}

, az eredményt

r_{0} / D_{1}

első nem eltűnő hatványáig sorbafejtve add meg. Felhasználhatod, hogy

{(1 + x)}^{a} \approx 1 + a x

, ha

x ≪ 1

.
3.f. Add meg a

τ

forgatónyomaték számértékét, felhasználva, hogy

ϑ = 3^{\circ}

, és

m = 3, 6 \cdot 10^{16}

kg. (Megjegyzendő, hogy ennek a tömegnek a nagyságrendje

10^{- 8}

-szorosa a Föld tömegének.)
Felhasználva, hogy a forgatónyomaték az impulzusmomentum időbeli változási sebessége, határozd meg a Föld‐Hold távolság éves növekedésének jelenlegi értékét! Ehhez fejezd ki a Hold impulzusmomentumát kizárólag az

M_{H}

M_{F}

D_{1}

és

G

mennyiségekkel.
3.g. Határozd meg a Föld‐Hold távolság évenkénti növekedésének jelenlegi értékét!
Végül becsüld meg, hogy mennyivel nő egy év alatt egy nap hossza.
3.h. Add meg, hogy egy év alatt mennyivel csökken

ω_{F1}

, és jelenleg mennyivel nő egy nap hossza egy év alatt!

4. Hová lesz az energia? Az impulzusmomentummal szemben, ami megmarad, a rendszer teljes mechanikai energiája (forgási és gravitációs) nem állandó. Az utolsó részben ezt a kérdést vizsgáljuk.
4.a. Add meg a Föld‐Hold rendszer teljes

E

mechanikai energiáját (forgási- plusz gravitációs energiáját) az égitestek jelenlegi helyzetében! Az eredményt kizárólag az

I_{F}

ω_{F1}

M_{H}

M_{F}

D_{1}

és

G

mennyiségekkel fejezd ki!
4.b. Fejezd ki az

E

energia megváltozását,

Δ E

-t a

D_{1}

és

ω_{F1}

mennyiségek megváltzásával! Határozd meg

Δ E

számszerű értékét egy évre vonatkoztatva, felhasználva a

D_{1}

és

ω_{F1}

mennyiségek megváltozásának

3 g

és

3 h

pontban kiszámolt értékét!
Most ellenőrizzük, hogy az így kapott energiaveszteség összeegyeztethető azzal a hővel, amit a Hold árapály hatása hoz létre a Földön. Tegyük föl, hogy a dagály átlagosan 0,5 m-rel emel meg egy

h = 0, 5

m mély vízréteget, a Föld teljes felszínén. (Az egyszerűség kedvéért tegyük föl, hogy a Föld teljes felszíne vízzel van borítva.) Ez az emelkedés (dagály) minden nap kétszer következik be. Tegyük fel továbbá, hogy a víz viszkozitásának következtéban ennek a gravitációs energiának 10%-a disszipálódik hő formájában apály alkalmával. A víz sűrűsége

ϱ_{víz} = 10^{3} {kg m}^{- 3}

, és a Föld felszínén a gravitációs gyorsulás

g = 9, 8 {m s}^{- 2}

.
4.c. Mekkora a szóban forgó felületi vízréteg tömege?
4.d. Határozd meg, hogy mennyi energia disszipálódik egy év alatt! Milyen viszonyban áll ez a Föld‐Hold rendszer mechanikai energiájának jelenlegi évenkénti csökkenésével?

2. feladat. Lézeres Doppler-hűtés és optikai szirupok

Ennek a feladatnak az a célja, hogy egyszerű elméleti megfontolással megértsed a ,,lézeres hűtés'' és az ,,optikai szirup'' jelenségeket. Ez azt jelenti, hogy semleges atomok (általában alkáli fémek) nyalábját egymással szemben haladó, azonos frekvenciájú lézersugarakkal hűtjük. Ezért kapott 1997-ben fizikai Nobel-díjat S. Chu, P. Phillips és C. Cohen-Tannoudji.
A hátsó belső borító jobb felső képe nátrium atomokat ábrázol (a fényes pont középen), melyek három, egymásra merőleges lézersugár-pár kereszteződésében vannak csapdázva. A csapda területét szokás ,,optikai szirup''-nak (,,optical molasses'') nevezni, mivel a disszipatív optikai erő a szirupon áthaladó testekre ható viszkózus erőre emlékeztet.
Ebben a feladatban egy foton és egy atom egyszerű kölcsönhatását és a disszipációs mechanizmust fogod vizsgálni egy dimenzióban.

I. rész: A lézeres hűtés alapjai
Tekints egy

m

tömegű atomot, amely a

+ x

irányban,

v

sebességgel mozog. Az egyszerűség kedvéért vizsgáld a problémát egy dimenzióban, azaz ne foglalkozz az

y

és

z

irányokkal (4. ábra). Az atomnak két belső energiaszintje van. Az alapállapot energiáját nullának tekintjük, a gerjesztett állapot energiája pedig

ℏ ω_{0}

, ahol

ℏ = h / 2 π

. Az atom kezdetben alapállapotban van. Egy lézersugár, melynek a laboratórium koordináta-rendszerében mért körfrekvenciája

ω_{L}

, a

- x

irányban halad, és ütközik egy atommal. Kvantummechanikai szempontból a lézersugár nagyszámú egyforma fotonból áll, melyek energiája

ℏ ω_{L}

és impulzusa

- ℏ q

. A fotont elnyelheti egy atom, amely azt később spontán kibocsátja; ez a kibocsátás (emisszió) azonos valószínűséggel történhet a

+ x

és a

- x

irányban. Mivel az atom nemrelativisztukus sebességgel mozog,

v / c ≪ 1

(ahol

c

a fénysebesség). Vedd figyelembe azt is, hogy

ℏ q / m v ≪ 1

, azaz az atom impulzusa sokkal nagyobb egy foton impulzusánál. A válaszaidban mindkét mennyiségnek csak az elsőrendű (lineáris) tagjait vedd figyelembe.

4. ábra. Egy

m

tömegű,

v

sebességű, a

+ x

irányban haladó atom, amely egy

ℏ ω_{L}

energiájú és

- ℏ q

impulzusú fotonnal ütközik. Az atomnak két belső állapota van

ℏ ω_{0}

energiakülönbséggel

Feltételezd, hogy a lézer

ω_{L}

körfrekvenciája úgy van hangolva, hogy a mozgó atom rendszeréből nézve rezonanciában van az atom belső átmenetével. Válaszolj a következő kérdésekre:

1. Elnyelés (abszorpció)
1.a. Add meg a foton elnyelésének (abszorpciójának) rezonanciafeltételét!
1.b. Add meg az atom

p_{a}

impulzusát az elnyelés után, a laboratórium rendszeréből nézve!
1.c. Add meg az atom

ε_{a}

teljes energiáját az elnyelés után, a laboratórium rendszeréből nézve!

2. Egy foton spontán kibocsátása (emissziója) a

- x

irányban
Az ütköző foton elnyelődése (abszorbciója) után valamennyi idővel az atom egy fotont bocsáthat ki (emittálhat) a

- x

irányban.
2.a. Add meg a kibocsátott foton

ε_{f}

energiáját a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
2.b. Add meg a kibocsátott foton

p_{f}

impulzusát a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
2.c. Add meg az atom

p_{a}

impulzusát a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
2.d. Add meg az atom

ε_{a}

teljes energiáját a

- x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!

3. Egy foton spontán kibocsátása (emissziója) a

+ x

irányban
Az ütköző foton elnyelődése (abszorbciója) után valamennyi idővel az atom egy fotont bocsáthat ki (emittálhat) a

+ x

irányban.
3.a. Add meg a kibocsátott foton

ε_{f}

energiáját a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
3.b. Add meg a kibocsátott foton

p_{f}

impulzusát a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
3.c. Add meg az atom

p_{a}

impulzusát a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!
3.d. Add meg az atom

ε_{a}

teljes energiáját a

+ x

irányú emissziós folyamat után, a laboratórium rendszeréből nézve!

4. Átlagos kibocsátás (emisszió) az elnyelés (abszorpció) után
A foton spontán kibocsátása egyforma valószínűséggel történhet a

- x

vagy a

+ x

irányban. Ezt figyelembe véve válaszolj a következő kérdésekre:
4.a. Add meg a kibocsátott foton

ε_{f}

átlagos energiáját az emissziós folyamat után!
4.b. Add meg a kibocsátott foton

p_{f}

átlagos impulzusát az emissziós folyamat után!
4.c. Add meg az atom

ε_{a}

átlagos teljes energiáját az emissziós folyamat után!
4.d. Add meg az atom

p_{a}

átlagos impulzusát az emissziós folyamat után!

5. Energia- és impulzusátadás
Tekints egy teljes egyfotonos elnyelési-kibocsátási (abszorpciós-emissziós) folyamatot, ahogy azt az eddigiekben tárgyaltuk. A lézersugár és az atom között egy eredő átlagos impulzus- és energiaátadás figyelhető meg.
5.a. Add meg az atom

Δ ε

átlagos energiaváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!
5.b. Add meg az atom

Δ p

átlagos impulzusváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!

6. Energia- és impulzusátadás egy

+ x

irányú lézersugárral
Tekints most egy olyan lézersugarat, amelynek

ω'_{L}

a körfrekvenciája és a

+ x

irányban halad, miközben az atom szintén a

+ x

irányban halad

v

sebességgel. Azt feltételezve, hogy az atom belső átmenete és a lézersugár között az atom rendszeréből nézve teljesül a rezonanciafeltétel, válaszolja következő kérdésekre:
6.a. Add meg az atom

Δ ε

átlagos energiaváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!
6.b. Add meg az atom

Δ p

átlagos impulzusváltozását egy teljes egyfotonos elnyelési-kibocsátási folyamat után!

II. rész: Disszipáció és az optikai szirup alapjai
A természetben a kvantumfolyamatokat elkerülhetetlenül bizonytalanság kíséri. Így az a tény, hogy az atom az elnyelés után véges idővel bocsát ki egy fotont, azzal a következménnyel jár, hogy a rezonanciafeltétel nem teljesül egzaktul, úgy ahogy azt eddig tárgyaltuk. Azaz a lézersugár

ω_{L}

és

ω'_{L}

körfrekvenciája bármilyen értéket felvehet, és az elnyelés (abszorpció) mégis bekövetkezhet. Az elnyelés különböző (kvantum)valószínűséggel történik, és ‐ mint ahogy azt sejteni lehet ‐ a legnagyobb valószínűséggel éppen a rezonanciafeltétel egzakt teljesülésekor. Egy foton elnyelése és kibocsátása között átlagosan eltelő időt a gerjesztett állapot élettartamának nevezzük, és így jelöljük:

Γ^{- 1}

.
Tekintsünk egy

N

atomból álló, a laboratórium koordinátarendszeréhez viszonyítva nyugalomban lévő atomhalmazt, és egy rá eső

ω_{L}

körfrekvenciájú lézersugarat. Az atomok folyamatosan fotonokat nyelnek el és bocsátanak ki, úgy, hogy átlagosan

N_{g}

atom van gerjesztett állapotban (és így

N - N_{g}

atom alapállapotban). Kvantummechanikai számítás eredményeként adódik, hogy:

\begin{matrix} N_{g} = N \frac{Ω_{R}^{2}}{{(ω_{0} - ω_{L})}^{2} + \frac{Γ^{2}}{4} + 2 Ω_{R}^{2}}, \end{matrix}

ahol

ω_{0}

az atomi átmenet rezonancia-körfrekvenciája, és

Ω_{R}

az úgynevezett Rabi-frekvencia;

Ω_{R}^{2}

arányos a lézersugár intenzitásával. Láthatod, hogy ez az érték ‐ ahogy már említettük ‐ akkor is különbözik nullától, ha

ω_{0}

nem egyezik meg a lézersugár

ω_{L}

körfrekvenciájával. Az előbbi eredményt úgy is kifejezhetjük, hogy időegységenként bekövetkező elnyelési-kibocsátási (abszorpciós-emissziós) folyamatok száma

N_{g} Γ

.
Tekintsd az 5. ábrán látható fizikai elrendezést, ahol két szemben haladó lézersugár egymással azonos, de amúgy tetszőleges

ω_{L}

körfrekvenciával ütközik az

N

atomból álló,

+ x

irányban

v

sebességgel mozgó gáznak.

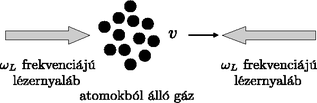5. ábra. Két szemben haladó lézersugár egymással azonos, de amúgy tetszőleges

ω_{L}

körfrekvenciával ütközik az

N

atomból álló,

+ x

irányban

v

sebességgel mozgó gáznak

7. A lézer által az atomnyalábra kifejtett erő
7.a. Az eddigi információk alapján határozd meg azt az erőt, amit a lézersugár kifejt az atomnyalábra! Használd ki, hogy

m v ≫ ℏ q

.
8. Kissebességű határeset. Most tételezd fel, hogy az atomok sebessége elég kicsi ahhoz, hogy az erő a

v

sebesség első rendű tagjával közelíthető.
8.a. Határozd meg a 7.a. feladatban meghatározott erő kifejezését ebben a közelítésben!
Felhasználva ezt az eredményt megkeresheted annak a feltételét, hogy a lézersugár az atomnyalábot gyorsítja, lassítja, illetve nem hat rá.
8.b. Add meg annak a feltételét, hogy az erő pozitív (gyorsítja az atomokat)!
8.c. Add meg annak a feltételét, hogy az erő nulla!
8.d. Add meg annak a feltételét, hogy az erő negatív (lassítja az atomokat)!
8.e. Most tedd fel, hogy az atomok

- v

sebességgel mozognak (a

- x

irányban). Add meg annak a feltételét, hogy az erő lassítsa az atomokat!
9. Optikai szirup. Negatív erő esetében egy disszipatív súrlódó erőt kapunk. Tedd fel, hogy kezdetben, amikor

t = 0

, a gáz atomjai

v_{0}

sebességgel mozognak.
9.a. Kissebességes közelítésben határozd meg az atomok sebességét azután, hogy a lézersugarak

τ

ideje be vannak kapcsolva.
9.b. Most tételezd fel, hogy a gáz atomjai kezdetben

T_{0}

hőmérsékleten termikus egyensúlyban vannak. Határozd meg a

T

hőmérsékletet azután, hogy a lézersugarak

τ

ideje be vannak kapcsolva.
(A modell azonban nem teszi lehetővé tetszőlegesen kicsi hőmérséklet elérését.)

3. feladat. Miért olyan nagyok a csillagok?

A csillagok forró gázgömbök, melyek ragyogását a belsejükben lezajló magfúzió adja. Leggyakoribb esetben e folyamat során hidrogénből hélium keletkezik. Ebben a problémában klasszikus mechanikai, illetve kvantummechanikai fogalmak, valamint elektrosztatikai, termodinamikai összefüggések segítségével keressük a választ arra a kérdésre, hogy a gázgömbnek miért csak egy bizonyos mérete fölött indul be a fúziós reakció. Sőt, a hidrogén fúziójához szükséges kritikus tömeg és sugár értékét is meghatározzuk. (A Napról, mint csillagról látható kép a hátsó belső borítón jobbra középen.)
Fontos fizikai állandók:
gravitációs állandó:

G = 6, 7 \cdot 10^{- 11} m^{3} {kg}^{- 1} s^{2}

;
Boltzmann-állandó:

k = 1, 4 \cdot 10^{- 23} {J K}^{- 1}

;
Planck-állandó:

h = 6, 6 \cdot 10^{- 34} m^{2} {kg s}^{- 1}

;
proton tömege:

m_{p} = 1, 7 \cdot 10^{- 27}

kg;
elektron tömege:

m_{e} = 9, 1 \cdot 10^{- 31}

kg;
elemi töltés:

q = 1, 6 \cdot 10^{- 19}

C;
vákuum permittivitás:

ε_{0} = 8, 9 \cdot 10^{- 12} C^{2} N^{- 1} m^{- 2}

;
Nap sugara:

R_{N} = 7, 0 \cdot 10^{8}

m;
Nap tömege:

M_{N} = 2, 0 \cdot 10^{30}

kg.

1. Csillagok központi hőmérsékletének klasszikus becslése
Tegyük föl, hogy a csillagot formáló gáz tiszta ionizált hidrogén, azaz elektronok és protonok azonos arányú keveréke, mely ideális gázként viselkedik. A klasszikus fizika törvényei szerint két proton fúziójához az szükséges, hogy

10^{- 15}

méternél közelebb kerüljenek egymáshoz, mivel csak ilyen kis távolság esetén válik a rövidtávú magerő meghatározóvá. Azonban ahhoz, hogy ilyen közel kerüljenek egymáshoz, le kell győzniük a Coulomb-taszítást. Tegyük fel, hogy két klasszikus, pontszerű részecskének tekintett proton

v_{rms}

nagyságú, egymással ellentétes irányú sebességgel halad egymás felé egy egyenes mentén, és frontálisan ütközik. Itt

v_{rms}

a termodinamikai átlagsebesség (sebességnégyzet átlagának a gyöke; az index az angol root-mean-square kifejezésre utal).
1.a. Határozd meg azt a kritikus

T_{c}

hőmérsékletet, amely esetén két ütköző proton közti minimális

d_{c}

távolság éppen

10^{- 15}

m! A keresett értéket, és ebben a feladatban minden további számszerű eredményt két értékes jegyre adj meg!

2. Annak igazolása, hogy az előző hőmérséklet-becslés hibás
Ahhoz, hogy ellenőrizzük előző becslésünk megbízhatóságát, még egy független módszerre van szükségünk a csillagok központi hőmérsékletének meghatározására. Egy valódi csillag felépítése meglehetősen bonyolult, de néhány egyszerűsítő feltevés használatával a lényeget könnyen megérthetjük. A csillagok egyensúlyban vannak, ami azt jelenti, hogy se nem tágulnak, se nem húzódnak össze, mert a befelé mutató gravitációs erő egyensúlyt tart a kifelé mutató nyomással (6. ábra). Egy, a középponttól

r

távolságban levő gázréteg hidrosztatikai egyensúlyát a

\begin{matrix} \frac{Δ P}{Δ r} = - \frac{G M_{r} ϱ_{r}}{r^{2}} \end{matrix}

egyenlet fejezi ki, ahol

P

a gáz nyomása,

G

a gravitációs állandó,

M_{r}

a csillag

r

sugarú gömbön belül eső részének tömege,

ϱ_{r}

pedig a gázréteg sűrűsége.

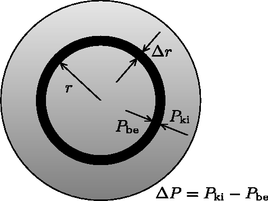6. ábra. A csillagok hidrosztatikai egyensúlyban vannak, a nyomás-változással a gravitáció tart egyensúlyt

A csillag központi hőmérsékletére nagyságrendi becslést kaphatunk, ha a paramétereknek a középpontban és a csillag felszínén felvett értékét használjuk, tehát a következő közelítésekkel élünk:

\begin{matrix} Δ P \approx P_{0} - P_{c}, \end{matrix}

ahol

P_{c}

a központi,

P_{0}

pedig a felületi nyomás. Mivel

P_{c} ≫ P_{0}

, feltehetjük, hogy

\begin{matrix} Δ P \approx - P_{c} . \end{matrix}

Ugyanezzel a közelítéssel élve, a ,,rétegvastagságra'' az adódik, hogy

\begin{matrix} Δ r \approx R, \end{matrix}

ahol

R

a csillag (teljes) sugara, valamint

\begin{matrix} M_{r} \approx M_{R} = M, \end{matrix}

ahol

M

a csillag teljes tömege.
A sűrűség közelíthető a középpontban felvett értékével,

\begin{matrix} ϱ_{r} \approx ϱ_{c} . \end{matrix}

Feltehetjük továbbá, hogy a nyomás az ideális gáztörvényből számolható.
2.a. Határozd meg a csillag középpontjában a

T_{c}

hőmérsékletet kizárólag a csillag sugarának, tömegének, valamint fizikai állandóknak a segítségével!
A fenti modell teszteléséhez vizsgáljuk meg a kapott eredmény egy egyszerű következményét:
2.b. A 2.a. pontban kapott egyenlőség alapján add meg a vizsgált csillagokra az

M / R

arány becsült értékét kizárólag fizikai állandók és

T_{c}

függvényében!
2.c. A

T_{c}

hőmérsékletnek az 1.a. pontban meghatározott értéke alapján határozd meg számszerűen a csillagok

M / R

arányának jósolt értékét!
2.d. Most számold ki a Nap esetén az

M_{Nap} / R_{Nap}

arányt, és ellenőrizd, hogy ez az érték sokkal kisebb, mint a 2.c. pontban meghatározott érték!

3. Csillagok központi hőmérsékletének kvantummechanikai becslése
A 2.d. pontban talált nagy eltérés azt sejteti, hogy

T_{c}

-nek az 1.a. pontban adott becslése nem helyes. Az ellentmondás kvantummechanikai effektusok figyelembevételével oldható fel. Eszerint a protonok hullámként viselkednek, és egyetlen proton a

λ_{p}

de Broglie-hullámhosszával azonos nagyságrendű területen ,,van szétkenve''. Ez azt jelenti, hogy ha a protonok között elért

d_{c}

minimális távolság a

λ_{p}

hullámhossz közelébe esik, akkor a két részecske kvantummechanikai értelemben ,,átfedésbe kerül'', és így képesek a fúzióra.
3.a. Feltéve, hogy a

v_{rms}

sebességgel haladó protonok esetén a fúzió feltétele

d_{c} = \frac{λ_{p}}{2^{1 / 2}}

, határozd meg

T_{c}

értékét csupán fizikai állandók segítségével!
3.b. Határozd meg a

T_{c}

hőmérsékletre a 3.a. pontban kapott kifejezés numerikus értékét!
3.c. A 3.b. pontban kapott érték valamint a 2.b. pontban levezetett kifejezés segítségével határozd meg az

M / R

arány becsült numerikus értékét csillagokra! Ellenőrizd, hogy ez az érték közel esik-e a megfigyelésekből származó

M_{Nap} / R_{Nap}

arányhoz!
Valóban, az úgynevezett fősorozatba eső csillagok (melyekben hidrogén fúziója zajlik, ,,normális'' csillagok) nagyon tág tömeghatárok között megfelelnek a fenti becslésnek.

4. Csillagok tömeg/sugár aránya
Az előző feladatban tapasztalt egyezés azt sejteti, hogy a Nap középponti hőmérsékletének becslésére a kvantummechanikai gondolatmenet helyes.
4.a. Az előző eredményt felhasználva mutasd meg, hogy minden olyan csillag esetén, melyben hidrogén-fúzió zajlik, az

M

tömeg és

R

sugár aránya állandó, mely kizárólag univerzális fizikai konstansoktól függ! Határozd is meg ezt az

M / R

arányt ezekre a csillagokra!

5. A legkisebb csillagok tömege és sugara
A 4.a. pontban kapott eredményből arra következtethetnénk, hogy bármely tömeggel létezhetnek hidrogén-fúziós ciklusban levő csillagok, feltéve, hogy az összefüggés feltétele teljesül. Ez a következtetés azonban helytelen.
A hidrogén-fúziós ciklusban levő csillagokban található gáz ideális gázként viselkedik. Ez azt jelenti, hogy az elektronok közti

d_{e}

tipikus távolság átlagos értéke nagyobb, mint az elektronok

λ_{e}

de Broglie-hullámhossza. Ellenkező esetben ugyanis az elektronok egy úgynevezett degenerált állapotban lennének, és a csillag másképp viselkedne. Felhívjuk a figyelmet arra a tényre, hogy a vizsgált csillag-típusban levő protonokat és elektronokat másként kezeljük. Protonok esetén a de Broglie-hullámok átfedése szükséges ahhoz, hogy a fúzió létrejöhessen, míg elektronok esetén a de Broglie hullámok nem fedhetnek át, mert különben az elektronokat nem kezelhetnénk ideális gázként.
A valóságban a csillagok belsejében levő gáz sűrűsége a középpont felé haladva nő. Ennek ellenére ebben a nagyságrendi becslésben tegyük föl, hogy a vizsgált csillag sűrűsége állandó. Ezen kívül felhasználhatjuk, hogy

m_{p} ≫ m_{e}

.
5.a. Határozd meg az

n_{e}

átlagos elektronszám-sűrűséget a csillag belsejében!
5.b. Határozd meg az elektronok közti

d_{e}

tipikus távolságot a csillag belsejében!
5.c. A

d_{e} \geq \frac{λ_{e}}{2^{1 / 2}}

feltétel használatával határozd meg egyenlettel a legkisebb olyan csillag sugarát, mely hidrogén-fúziós ciklusban lehet! (Ezek az ún. normál csillagok.) Tekintsd úgy, hogy a csillag középpontjában mért hőmérséklet a csillagban bárhol mérhető hőmérséklet tipikus értéke.
5.d. Határozd meg a lehető legkisebb normál csillag sugarának számértékét méterben is és a Nap sugarának (rádiuszának) egységében is!
5.e. Határozd meg a lehető legkisebb normál csillag tömegének számértékét kilogrammban is, és Naptömeg-egységben is!

6. Hélium-fúzió öregebb csillagokban
Ahogy a csillagok öregednek, majdnem az összes magjukban lévő hidrogént héliummá (He) alakították, így a további fénykibocsátás érdekében arra kényszerülnek, hogy elkezdjék a hélium fuzionálását nehezebb elemekké. A hélium mag két protonból és két neutronból áll, így a töltése kétszerese, a tömege kb. négyszerese a protonénak. Láttuk korábban, hogy a proton fúziójának feltétele

d_{c} = \frac{λ_{p}}{2^{1 / 2}}

.
6.a. Add meg a megfelelő feltételt a hélium magokra vonatkozóan, és határozd meg a hélium magok

v_{rms}

(He) négyzetes átlagsebességét, valamint a hélium fúzióhoz szükséges

T

(He) hőmérsékletet!

^{$^{*}$}A hivatalos megoldást és a mérési feladatot a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre.