Cím:	Megoldásvázlatok a 2009. szeptemberi emelt szintű gyakorló feladatokhoz
Szerző(k):	Simon János
Füzet:	2009/október, 402 - 407. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Mutassuk meg, hogy az $f\left(x\right)=\frac{1}{x^2}$ (ahol $x\ne 0$ valós szám) hozzárendeléssel megadott függvényre minden $a\ne 0$, $b\ne 0$ valós számpár esetén teljesül, hogy $\begin{array}{c}{\displaystyle f\left(a\right)+f\left(b\right)+2ab\cdot f\left(ab\right)=\frac{f\left(ab\right)}{f\left(a+b\right)}\mathrm{.}}\end{array}$  (11 pont)   Megoldás. Végezzük el a behelyettesítést a bal oldalon: $\begin{array}{c}{\displaystyle f\left(a\right)+f\left(b\right)+2ab\cdot f\left(ab\right)=\frac{1}{a^2}+\frac{1}{b^2}+2ab\cdot \frac{1}{{\left(ab\right)}^2}\mathrm{.}}\end{array}$ Ezt tovább alakítva: $\begin{array}{c}{\displaystyle \frac{a^2+b^2+2ab}{a^2{b}^2}=\frac{{\left(a+b\right)}^2}{a^2{b}^2}=\frac{\frac{1}{{\left(ab\right)}^2}}{\frac{1}{{\left(a+b\right)}^2}}\mathrm{.}}\end{array}$ Ami pontosan $\frac{f\left(ab\right)}{f\left(a+b\right)}$-vel egyenlő, és ezt szerettük volna igazolni.   2. A természetes számok sorozatából valamelyik számtól kezdve kiválasztjuk minden $12$. számot addig, míg a kiválasztott számok összege $2010$ lesz. A kiválasztott számok száma $10$-nél több, de $100$-nál kevesebb. Melyik számot választottuk ki először és összesen hány darabot?  (12 pont)   Megoldás. Legyen az először kiválasztott szám $x$ $\left(x\in N\right)$, a kiválasztott számok darabszáma pedig $k$ ($10<k<100$ és $k\in \text{N}$). Ezen számok összege: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x+\left(x+12\right)+\text{...}+\left(x+\left(k-1\right)\cdot 12\right)}& {\displaystyle =kx+12\left(1+\text{...}+\left(k-1\right)\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =kx+\frac{\left(k-1\right)k}{2}\cdot 12=2010.}\hfill \end{array}}$ Vagyis: $k\left(x+6k-6\right)=2010=2\cdot 3\cdot 5\cdot 67$. Ebből következik, hogy $k$ 10-nél nagyobb és 100-nál kisebb osztója a 2010-nek. A 2010-nek 3 db ilyen osztója van: 15; 30; 67. Ha $k=15$, akkor $x=134-84=50$. Ha $k=30$, akkor $x=67-174<0$. Ha $k=67$, akkor $x=30-396<0$. Tehát csak $k=15$ esetén kapunk megfelelő $x$-et. Az első kiválasztott szám az 50 és 15 db számot választottunk ki.   3. Mutassuk meg, hogy ha egy háromszög oldalaira teljesül az $a^2+b^2>5c^2$ egyenlőtlenség, akkor $c$ a háromszög legkisebb oldala.  (14 pont)   Megoldás. A háromszög-egyenlőtlenség miatt: $b+c>a$, amiből következik: $b^2+2bc+c^2>a^2$. Mindkét oldalhoz $b^2$-et adva: $\begin{array}{c}{\displaystyle 2b^2+2bc+c^2>a^2+b^2>5c^2\mathrm{.}}\end{array}$ Ezt rendezve: $b^2+bc-2c^2>0$, amit így is írhatunk: $b^2-bc+2bc-2c^2>0$, ennek szorzatalakja: $\left(b-c\right)\left(b+2c\right)>0$. Mivel a második tényező pozitív, ezért az elsőnek is pozitívnak kell lennie, azaz $b>c$. Hasonlóan belátható, hogy $a>c$, vagyis $c$ valóban a háromszög legkisebb oldala.   4. Van-e megoldása a $\text{sin}{}^{6}x+\text{sin}{}^{4}x+2\text{sin}{}^{2}x+\text{cos}{}^{2}x=4\text{sin}{}^{5}x$ egyenletnek a $\left]0;\frac{\pi }{2}\right[$-on?  (14 pont)   Megoldás. Mindkét oldal néggyel való osztása, majd a bal oldalon $\text{cos}{}^{2}x=1-\text{sin}{}^{2}x$ helyettesítése után a kapott egyenlet bal oldalának minden tagja pozitív. A számtani és a mértani közepek közötti egyenlőtlenség miatt: $\begin{array}{c}{\displaystyle \text{sin}{}^{5}x=\frac{\text{sin}{}^{6}x+\text{sin}{}^{4}x+\text{sin}{}^{2}x+1}{4}\ge \sqrt[4]{\text{sin}{}^{12}x}=\text{sin}{}^{3}x\mathrm{.}}\end{array}$ Vagyis: $\text{sin}{}^{3}x\left(\text{sin}{}^{2}x-1\right)\ge 0$. Mivel a megadott intervallumon $\text{sin}x\in \left]0;1\right[$, azért az első tényező pozitív, a második tényező negatív, azaz a szorzatuk negatív. Tehát ezen az intervallumon nincs megoldása az egyenletnek.   II. rész   5. Oldjuk meg a valós számok halmazán a következő egyenlőtlenséget: $\begin{array}{c}{\displaystyle x^2\cdot \text{log}{}_4\left(5x^2-2x-3\right)-x\cdot \text{log}{}_{\frac{1}{4}}\left(5x^2-2x-3\right)\le x^2+x\mathrm{.}}\end{array}$ (16 pont)   Megoldás. A logaritmus miatt: $5x^2-2x-3>0$, amiből kapjuk, hogy $x<-0\mathrm{,}6$ vagy $1<x$. Azonos alapra hozzuk a logaritmusokat; 0-ra rendezzük, majd szorzattá alakítjuk az egyenlőtlenséget: $\begin{array}{c}{\displaystyle x\left(x+1\right)\cdot \left[\text{log}{}_4\left(5x^2-2x-3\right)-1\right]\le 0.}\end{array}$ A 4-es alapú logaritmus függvény szigorúan monoton nő, ezért a harmadik tényező akkor nemnegatív, ha $\begin{array}{c}{\displaystyle 5x^2-2x-3\ge \mathrm{4,}\text{azaz}5x^2-2x-7\ge 0.}\end{array}$ Ebből kapjuk: $x\le -1$ vagy $1\mathrm{,}4\le x$. A három tényező előjelét számegyenesen ábrázolva és a logaritmus miatt tett kikötésünket is figyelembe véve a megoldáshalmaz: $\left\{-1\right\}\cup \left]1;1\mathrm{,}4\right]$.   6. A Stadion parkjában található ,,rúgófal'' felső lyukába $10\%$, az alsóba $40\%$ valószínűséggel talál be Márton. $a)$ Mindkét lyukra egyszer lőve mennyi a valószínűsége, hogy $\begin{array}{c}\end{array}$ A: egyszer sem talál; $\begin{array}{c}\end{array}$ B: egyszer talál? $b)$ Hányszor kell az alsó lyukra lőnie, hogy több mint $95\%$ valószínűséggel legalább egyszer beletaláljon? $c)$ Mennyi a valószínűsége, hogy háromszor az alsóra, majd háromszor a felsőre lőve pontosan egyszer talál? $d)$ Krisztián észrevette, hogy Marci találati valószínűsége nem konstans. Találat után (az eredeti valószínűség) $\frac{1}{10}$ részével nő, ha nem talál, $\frac{1}{10}$ részével csökken az eredeti találati valószínűség. Marci kétszer lő az alsó lyukra. Mekkora a valószínűsége, hogy pontosan egyszer talál?  (16 pont)   Megoldás. $a)$ A: $0\mathrm{,}9\cdot 0\mathrm{,}6=0\mathrm{,}54$. B: $0\mathrm{,}9\cdot 0\mathrm{,}4+0\mathrm{,}1\cdot 0\mathrm{,}6=0\mathrm{,}42$. $b)$ Legyen a rúgások száma $n$. Ekkor: $1-0\mathrm{,}{6}^n>0\mathrm{,}95$. Az egyenlőtlenség megoldáshalmazából a legkisebb pozitív egész számot keressük. Elvégezzük a következő átalakításokat: $\begin{array}{c}{\displaystyle 0\mathrm{,}05>0\mathrm{,}{6}^n\mathrm{,}\text{lg}0\mathrm{,}05>n\text{lg}0\mathrm{,}\mathrm{6,}n>\frac{\text{lg}0\mathrm{,}05}{\text{lg}0\mathrm{,}6}\approx 5\mathrm{,}86.}\end{array}$ Vagyis legalább 6-szor kell lőnie. $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot 0\mathrm{,}4\cdot 0\mathrm{,}{6}^2\cdot 0\mathrm{,}{9}^3+\left(\genfrac{}{}{0ex}{}{3}{1}\right)\cdot 0\mathrm{,}{6}^3\cdot 0\mathrm{,}1\cdot 0\mathrm{,}{9}^2\approx 0\mathrm{,}367.}\end{array}$ c) A keresett valószínűség: kb. 0,367. $d)$ $0\mathrm{,}4\cdot 0\mathrm{,}56+0\mathrm{,}6\cdot 0\mathrm{,}36=0\mathrm{,}44$. Ebben az esetben Marci 0,44 valószínűséggel talál be pontosan egyszer.   7. Adott a derékszögű koordinátarendszerben a $K\left(-2;3\right)$ középpontú $r=5$ sugarú kör és három pont: $A\left(6;2\right)$, $B\left(-3;5\right)$ és $C\left(-5;y_0\right)$, ahol $y_0>0$. $a)$ Mekkora a kör $AB$ egyenesre illeszkedő húrjának hossza? $b)$ A $C$ pont illeszkedik a körre. A kör $C$-ben húzott érintője legyen az $e$ egyenes. Mekkora területű az a háromszög, amelyet az $e$ egyenes, az $y$ tengely és az $AB$ egyenes fog közre?  (16 pont)   Megoldás. $a)$ Az $AB$ egyenes egyenlete: $y=-\frac{1}{3}x+4$. A kör egyenlete: ${\left(x+2\right)}^2+{\left(y-3\right)}^2=25$.     Meghatározzuk a metszéspontjaik koordinátáit. Az $y$ helyére $-\frac{1}{3}x+4$ behelyettesítésével a kör egyenletét a következő alakra rendezzük: $\begin{array}{c}{\displaystyle 0=\frac{10}{9}{x}^2+\frac{10}{3}x-20.}\end{array}$ A másodfokú egyenlet megoldásai: $x_1=3$, $x_2=-6$. Vagyis a metszéspontok: $P_1\left(3;3\right)$, $P_2\left(-6;6\right)$; $P_1{P}_2=\sqrt[]{9^2+3^2}=\sqrt[]{90}=3\sqrt[]{10}$. Az $AB$ egyenesre illeszkedő húr hossza: $3\sqrt[]{10}$. $b)$ Mivel $C$ illeszkedik a körre, azért ${\left(-5+2\right)}^2+{\left(y_0-3\right)}^2=25$. Az $y_0^2-6y_0-7=0$ másodfokú egyenletet kaptuk, melynek megoldásai: $y_0=7$ vagy $y_0=-1$. Mivel $y_0>0$, azért $C\left(-5;7\right)$. A C-beli $e$ érintő egyenlete: $3x-4y=-43$. Az $AB$ egyenes egyenlete: $\frac{1}{3}x+y=4$. A két egyenes $Q$ metszéspontját kiszámítjuk: $\begin{array}{c}{\displaystyle Q\left(-\frac{81}{13};\frac{79}{13}\right)\mathrm{.}}\end{array}$ Az $e$ érintő és az $y$ tengely metszéspontja: $R\left(0;\frac{43}{4}\right)$. Az $AB$ egyenes és az $y$ tengely metszéspontja: $S\left(0;4\right)$. Vagyis a háromszög $RS$ oldalának hossza: $RS=\frac{27}{4}$. Ezen oldalhoz tartozó magasság hossza: $m=\frac{81}{13}$. 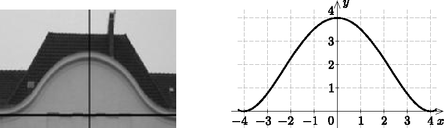A keresett terület: $\begin{array}{c}{\displaystyle t=\frac{\frac{27}{4}\cdot \frac{81}{13}}{2}=\frac{2187}{104}\approx 21\mathrm{,}03.}\end{array}$   8. Egy felújításra váró ház 8 m széles és 4 m magas oromzatát mutatja a mellékelt ábra. Az oromzat ívét leíró görbe érintője a végpontokban vízszintes. Az építész a görbét az $f\left(x\right)=a{x}^4+b{x}^2+c$ függvény grafikonjával szeretné megadni.     $a)$ Határozzuk meg az $f\left(x\right)$ függvény hozzárendelési szabályában szereplő $a$, $b$ és $c$ konstansokat. $b)$ Minimum hány doboz festékre lesz szükség az oromzat kétszeri újrafestéséhez, ha $1\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$-re $350\text{c<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$ festék szükséges, és $2$ literes, $4$ literes, illetve $5$ literes kiszerelésben kapható a festék?  (16 pont)   Megoldás. $a)$ Az $x=0$ helyettesítéssel kapjuk, hogy $f\left(0\right)=4=c$. Tudjuk, hogy $f\left(-4\right)=f\left(4\right)=0=256a+16b+4$. Tudjuk továbbá, hogy $f\text{'}\left(x\right)=4a{x}^3+2bx$, vagyis $f\text{'}\left(4\right)=0=256a+8b$. A következő egyenletrendszer megoldásával kapjuk a hiányzó konstansokat: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cccc}\hfill {\displaystyle 256a}& \hfill {\displaystyle +16b}& \hfill {\displaystyle +4}& \hfill {\displaystyle =\mathrm{0,}}\\ \hfill {\displaystyle 256a}& \hfill {\displaystyle +8b}& \hfill {\displaystyle }& \hfill {\displaystyle =0.}\end{array}}\}}\end{array}$ Azaz: $a=\frac{1}{64}$, $b=-\frac{1}{2}$. Tehát a keresett konstansok: $a=\frac{1}{64}$, $b=-\frac{1}{2}$, $c=4$. $b)$ Az oromzatot leíró függvény hozzárendelési szabálya: $f\left(x\right)=\frac{1}{64}{x}^4-\frac{1}{2}{x}^2+4$. A homlokzat területe: $\begin{array}{c}{\displaystyle T=\underset{-4}{\overset{4}{\int }}\left(\frac{1}{64}{x}^4-\frac{1}{2}{x}^2+4\right)dx={\left[\frac{x^5}{320}-\frac{x^3}{6}+4x\right]}_{-4}^4=\frac{256}{15}\approx 17.}\end{array}$ A szükséges festék térfogata cm${}^3$-ben: $V=17\cdot 2\cdot 350=11900$, ami 11,9 liter. Tehát minimum 3 doboz festékre lesz szükség (2 db 5 literesre és 1 db 2 literesre vagy 3 db 4 literesre).   9. Architectos fejedelem három fiával és seregeivel elfoglalt egy várost. A városfal három sarkán három egyforma négyzetes oszlop alakú torony állt, melyek alapéle 8 m, magasságuk 40 m volt. A győzelem emlékére a három fiú a három tornyot átalakítatta. Mindhárom átépítés nagyon hasonló volt egymáshoz. Az eredeti tornyok fedőlapjainak szomszédos élfelezőpontjait összekötő szakaszok mentén levágtak négy egyforma sarkot. Ezeket a megmaradt fedőlapra ültették az ábrának megfelelően úgy, hogy az új toronytető egymáshoz kapcsolódó rombuszokból állt.     A legidősebb fiú tornyának felszíne nem változott az átépítés után. A középső fiú úgy végezte el az átalakítást, hogy a torony teljes felszíne a lehető legkisebb lett. A legfiatalabb fiú tornyán a szomszédos tetősíkok ${120}^{\circ }$-os szöget zártak be. Adjuk meg az átépített tornyok magasságát.  (16 pont)   Megoldás. Jelöljük $h$-val, hogy mennyivel lesz magasabb az új torony az eredetinél. A rombusz (ábrán is látható) fél átlójának hossza legyen $b$, a másik átló $4\sqrt[]{2}$ hosszúságú. Az eredeti torony felszíne: $\begin{array}{c}{\displaystyle A=4\cdot 40\cdot 8+8\cdot 8=1344.}\end{array}$ Az új tető felszíne: $\begin{array}{c}{\displaystyle A=4\cdot \frac{4\sqrt[]{2}\cdot 2b}{2}=16b\cdot \sqrt[]{2}\mathrm{.}}\end{array}$ A Pitagorasz-tétel alapján: $b=\sqrt[]{8+h^2}$.     Az eredeti felszín csökken a fedőlap és az oldallapokon lévő háromszögek területével: $\begin{array}{c}{\displaystyle 8\cdot 8+8\cdot \frac{4h}{2}=64+16h\mathrm{.}}\end{array}$ Ennek és az új tető felszínének egyenlőnek kell lennie, hogy ne változzon a felszín: $\begin{array}{c}{\displaystyle 64+16h=16\sqrt[]{2}\cdot \sqrt[]{8+h^2}\mathrm{.}}\end{array}$ Oszthatunk 16-tal: $\begin{array}{c}{\displaystyle 4+h=\sqrt[]{16+2h^2}\mathrm{.}}\end{array}$ Négyzetre emelhetjük mindkét oldalt: $\begin{array}{c}{\displaystyle 16+8h+h^2=16+2h^2\mathrm{,}\text{azaz}0=h^2-8h=h\left(h-8\right)\mathrm{.}}\end{array}$ Csak a $h=8$ lehet a megoldás. A hosszúság adatok méterben voltak adva, ezért ez a torony 8 méterrel lett magasabb. A legidősebb fiú tornya az átépítés után 48 méter magas lett. A középső fiú által átépített új torony felszíne: $\begin{array}{c}{\displaystyle A\left(h\right)=1344-\left(64+16h\right)+16\sqrt[]{16+2h^2}=1280-16h+16\sqrt[]{16+2h^2}\mathrm{.}}\end{array}$ Ennek a függvénynek keressük a minimumhelyét. Ehhez szükségünk van a függvény deriváltjának zérushelyére: $\begin{array}{c}{\displaystyle A\text{'}\left(h\right)=-16+16\cdot \frac{1}{2\sqrt[]{16+2h^2}}\cdot 4h=\frac{16}{\sqrt[]{16+2h^2}}\left(2h-\sqrt[]{16+2h^2}\right)=0.}\end{array}$ Vagyis: $2h=\sqrt[]{16+2h^2}$, amiből kapjuk, hogy $0=16-2h^2$. Ennek pozitív gyöke: $h=2\sqrt[]{2}$. Ezen a helyen az első derivált negatívból pozitívba vált, tehát a felszínnek itt valóban minimuma van. A középső fiú tornya az átépítés után $40+2\sqrt[]{2}$, azaz kb. 42,8 méter magas lett. A legfiatalabb fiú tornyán két szomszédos =rombusz közös oldalára bocsátott közös talppontú magasságai által bezárt szög: ${120}^{\circ }$, a rombusz magassága $m$, oldala: $\sqrt[]{16+h^2}$. A rombusz területe: $\begin{array}{c}{\displaystyle \sqrt[]{16+h^2}\cdot m=\frac{4\sqrt[]{2}\cdot 2b}{2}=4\sqrt[]{2}\cdot \sqrt[]{8+h^2}\mathrm{,}\text{amiből}m=\frac{4\sqrt[]{16+2h^2}}{\sqrt[]{16+h^2}}\mathrm{.}}\end{array}$ A 8 egység alapú $m$ szárú egyenlőszárú háromszög szárszöge ${120}^{\circ }$ (a két szomszédos tetőlap hajlásszöge): $\begin{array}{c}{\displaystyle \text{sin}\frac{{120}^{\circ }}{2}=\frac{4}{m}=\sqrt[]{\frac{16+h^2}{16+2h^2}}=\frac{\sqrt[]{3}}{2}\mathrm{,}\text{azaz:}\frac{16+h^2}{16+2h^2}=\frac{3}{4}\mathrm{,}}\end{array}$ amiből: $64+4h^2=48+6h^2$, vagyis: $8=h^2$. Kapjuk, hogy $h=2\sqrt[]{2}$. A legfiatalabb fiú tornya is az átépítés után $40+2\sqrt[]{2}$, azaz kb. 42,8 méter magas lett.