Kezdőlap


Cím:	12. Román‐magyar előolimpiai fizikaverseny
Füzet:	2009/szeptember, 367 - 370. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Egyenlítői gravitációs gyűrű a Nap felületén. A Nap tengelykörüli forgásának következtében az egyenlítőnél egy kicsit nagyobb a sugara, mint a sarkoknál, így az anyageloszlás a Nap forgástengelye körül nem gömbszimmetrikus. Emiatt precesszálnak a bolygópályák a Naprendszerben (csúszik el a perihelium helye). Egy egyszerű modellben úgy tekinthetjük, hogy a Nap forgása miatt a Nap egyenlítőjén egy gravitációs gyűrű alakul ki a Nap felületén, melynek vastagsága elhanyagolható, tömege pedig $M ≪ M_{S}$ , ahol $M_{S}$ a Nap tömege (beleértve a gyűrű tömegét is).
Ennek a hatásnak a bizonyítására feltételezzük, hogy a Nap anyaga egyenletesen és szimmetrikusan oszlik el a bolygópályára merőleges tengely körül, és a Nap‐bolygó rendszer gravitációs potenciális energiája, a javasolt modellnek megfelelően, amikor az $m$ tömegű bolygó távolsága a Naptól $r ≫ R$ , a következő kifejezéssel adható meg:

\begin{matrix} E_{p} = - \frac{k}{r} [1 + \frac{1}{2} J_{2} {(\frac{R}{r})}^{2} - \frac{3}{8} J_{4} {(\frac{R}{r})}^{4} + \frac{5}{16} J_{6} {(\frac{R}{r})}^{6} + ...], \end{matrix}

ahol

R

a Nap sugara. A

J_{2}, J_{4}, J_{6}, ...

konstansok a Nap anyagának pontos eloszlásától függenek.

a)

Kvalitatív érvekkel határozd meg az

E_{p}

gravitációs potenciális energia fenti képletében szereplő

k

értékét. Az általános tömegvonzás

γ

állandóját tekintsd ismertnek.
Határozd meg az

E_{p}

gravitációs potenciális energia fenti képletében szereplő

J_{2}

állandó értékét, felhasználva a javasolt modellt. Használhatod a következő közelítést:

\begin{matrix} {(1 + α)}^{n} ≅ 1 + n α + \frac{1}{2} n (n - 1) α^{2}; α ≪ 1. \end{matrix}

b)

Olyan elliptikus bolygópálya, amelynek kicsi az excentricitása, és a bolygópálya csak nagyon kicsit tér el az egyenlítői körpályától, úgy is felfogható, hogy a bolygó nagyon kis amplitudójú sugárirányú rezgést végez az

r = r_{0}

távolság körül, és ez a rezgés rátevődik a bolygó Nap körüli körmozgására. (Ha ezt a folyamatot a perdületmegmaradás törvénye alapján vizsgáljuk, akkor kiderül, hogy a sugárirányú rezgés mindenképp együttjár egy azonos periódusidejű érintőirányú rezgéssel is. Ebben a feladatban ezt a hatást elhanyagoljuk.)
Határozd meg a bolygó sugárirányú rezgésének periódusidejét, ha tudjuk, hogy

J_{2} = 0

. A bolygó keringési ideje a Nap körül

T_{k}

. Feltéve, hogy

J_{2} = 0

, írd fel a bolygó mozgási energiáját a következő mennyiségek függvényében: a bolygó

p_{rad}

sugárirányú impulzusa; a bolygó

L

perdülete; a bolygó

m

tömege és a bolygó Naptól mért

r

távolsága.

c)

Figyelembe véve, hogy a bolygó perdülete állandó (

L =

konstans), a Nap‐bolygó rendszer összenergiájának minden olyan tagját, ami nem függ a sugárirányú impulzustól, feleltess meg egy a bolygó helyétől függő

V_{eff} = V_{eff} (r)

effektív gravitációs potenciálnak. Az effektív gravitációs potenciál bevezetése a bolygó mozgását csak sugárirányú mozgásra korlátozza.
Határozd meg azt az

r_{0}

távolságot, ahol az

F_{eff} = \frac{d V_{eff}}{d r}

effektív gravitációs erő nulla.

d)

Felhasználva a feladatban javasolt közelítést, határozd meg a Nap‐bolygó rendszer összenergiájának közelítő kifejezését

r = r_{0} + Δ r

helyen, ahol

Δ r ≪ r_{0}

, csak az

R^{2}

-nél nem nagyobb tagokat megtartva. Majd ezt a kifejezést összevetve a harmonikus oszcillátor összenergiájának kifejezésével, határozd meg a bolygó sugárirányú rezgésének

T_{r}

periódusidejét, ha

J_{2} \neq 0

.
Speciális eset: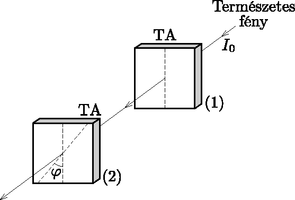

J_{2} = 0

2. Valóságos polárszűrők. Tudjuk, hogy a valóságos polárszűrő lemezek nem ideális polarizátorok, vagyis az áteresztési iránnyal (TA) párhuzamos elektromos rezgéseknek nem az összes energiáját engedik át, illetve a TA irányra merőleges elektromos rezgéseket nem nyelik el teljesen. Tegyük fel, hogy az első esetben az energia

α

hányada jut át, illetve a második esetben az energia

β

hányadát engedi át a polarizátor. A polárszűrő párra

I_{0}

intenzitású, közönséges, polarizálatlan fénnyaláb esik.

a)

Határozd meg egy valóságos polárszűrő pár által átengedett fénynyaláb

I

intenzitását abban az esetben, ha a polárszűrők az ábra szerint azonos optikai tengelyen helyezkednek el, és a két szűrő TA iránya által bezárt szög

φ

.
Vizsgáld meg az eredményt ideális polárszűrők esetén is! Az így kapott összefüggés az úgynevezett Malus-törvény.

b)

Adjunk összefüggést arra a

φ

szögre, amely esetén a valóságos polárszűrő pár által átengedett fényintenzitás megegyezik az ideális polárszűrő pár által átengedett fényintenzitással. Mi a feltétele annak, hogy ilyen

φ

szög létezzen?

c)

Legyen

α = 0, 95

és

β = 0, 05

egy adott polárszűrő párra. Számítsd ki az

I / I_{0}

arányt valóságos és ideális polárszűrő párok esetén, különböző

φ

szögek (

φ = 0^{\circ}

30^{\circ}

45^{\circ}

60^{\circ}

és

90^{\circ}

) esetén, ha rájuk közönséges, polarizálatlan fénysugarat bocsátunk.
Megjegyzés: Feltételezhetjük, hogy a fenti esetekben a fény a polárszűrők felületére merőlegesen halad. A polárszűrők vastagsága valamint a felületükről visszaverődő fény elhanyagolható.

3. A csodálatos szénatom.
A. A kovalens kötés több mint egy elektront tartalmaz. Két elektron csak akkor lehet ugyanabban a térrészben, ha ellentétes a spinjük. A kovalens kötés erősen irányított. A legegyszerűbb kovalens kötés a hidrogénmolekulában van, amely két protonból és két elektronból áll.

a)

Készíts egy elektromos modellt a stacionárius hidrogénmolekulára a hidrogénatom Bohr-modelljének analógiájára.

b)

Írd be a modellbe az elektron perdületének kvantálási feltételét az alapállapotban. Határozd meg a hidrogénmolekula geometriai paramétereit és a molekula kötési energiáját.
Hanyagold el a sugárzás okozta energiaveszteséget, és vedd figyelembe, hogy az elektron

m_{e}

tömege sokkal kisebb a proton

m_{p}

tömegénél. Tekintsd ismertnek a hidrogénatom első Bohr-sugarát (

a = 0, 533 \cdot 10^{- 10}

m) és a hidrogénre vonatkozó Rydberg-állandót (

R_{H} = 13, 6

eV).
B. A szén négy kovalens kötést tud képezni. Néha az atomoknak csak három közeli szomszédja van. Ilyenkor két szomszédhoz szimpla kovalens kötéssel, egyhez pedig dupla kovalens kötéssel kapcsolódik.
A gyémántban, melynek szerkezete az 1. ábrán látható, minden atom erősen kapcsolódik négy szomszédos atomhoz, melyek egy szabályos tetraéder csúcsaiban helyezkednek el. Az összes atom egy hatalmas molekulát alkot. A másik lehetőség az, hogy a szénatomok három szomszéddal hoznak létre kovalens kötést, így egy sík szerkezet jön létre, amit grafénnek nevezünk (2. ábra). Ha ilyen szerkezetek egymásra lapolódnak, grafit jön létre, melynek szerkezete a 3. ábrán látható.

1. ábra

2. ábra

3. ábra

A grafitkristály a 4. ábrán látható rombuszalapú hasáb ismételt egymásmellé rakásával is felépíthető,

α \sqrt[]{3}

élhosszal (ahol

α

egy

C - C

kötés hossza), ami a 3. ábrán szaggatott vonal jelöl.

4. ábra

A szén nanocső (carbon nano tube CNT) egy szénatomokból álló üres henger, melynek fala egy feltekert grafén réteg, ahogy az 5. ábrán látható. A nanocső szerkezetének leírásához a kiralitási vektort használjuk (6. ábra):

\vec{C_{n}} = n \vec{a_{1}} + m \vec{a_{2}}

, ahol

\vec{a_{1}}

\vec{a_{2}}

a hatszöges rács elemi vektorai,

n

m

pedig egész számok. A grafén úgy van feltekerve, hogy a

\vec{C_{n}}

kiralitási vektor hegye épp a kiindulási pontjába mutasson, míg a

\vec{T}

csavarási vektor párhuzamos a nanocső tengelyével. Az ilyen nanocsöveket mechanikai szenzorként lehet használni.

5. ábra

6. ábra

Ne felejtsd el, hogy a kovalens kötések hossza két szénatom között a grafénben, a grafitban és a gyémántban is

α = 0, 15

nm, két grafénréteg távolsága a grafitban

β = 0, 34

nm. A kötési energia a grafit vagy a gyémánt

C - C

szén kötéseiben

γ = 3, 6

eV, a grafit

C = C

szén kötéseiben pedig

δ = 6, 2

eV. A szénatom tömege

m_{0} = 19, 92 \cdot 10^{- 27}

kg, az Avogadro-szám

N_{A} = 6, 02 \cdot 10^{23} {mol}^{- 1}

. Annak ismeretében, hogy szublimáció molhője (ami annak felel meg, hogy a szénatomok szabaddá válnak a kristályból) gyémántra

E_{subl} = 716 {kJ\cdotmol}^{- 1}

, határozd meg:

c)

a gyémánt sűrűségét és a grafit sűrűségét;

d)

a gyémánt és a grafit kovalens kötésekből származó kölcsönhatási energiáját. A gyémánt esetében hasonlítsd össze ezt az energiát a szublimációs molhővel, és magyarázd meg az eredményt.
C. Ha egy egyik végén befogott

L

hosszúságú és

E

Young-modulusú rúd szabad végére a rúdra merőleges irányban

F

nagyságú erő hat, akkor a rúd végének

a

lehajlását az

a = - F \cdot L^{3} / (3 E \cdot J)

képlet adja meg. A

J

keresztmetszeti másodrendű nyomaték definíciója

J = \int_{S} y^{2} d S

, ahol

y

d S

elemi felületdarab távolsága a rúd neutrális zónájától (attól a síktól, ami nincs se összenyomva, se megnyújtva) és

S

a rúd keresztmetszete.
A szén nanocső hossza

L = 500

nm és királis vektora

\vec{C_{n}} = 20 \vec{a_{1}} + 20 \vec{a_{2}}

. Annak ismeretében, hogy a grafén Yung-modulusa

E = 10^{12}

Pa és a grafén sűrűsége

ϱ = 1900 kg\cdotm^{- 3}

(a grafént tömör hengeres rúdnak tekintve) határozd meg:

e)

a szén nanocső (CNT) rezgésének sajátfrekvenciáját;

f)

annak a

Δ m

tömegnek a nagyságát, amit a CNT szabad végére helyezve a frekvencia változása

Δ f = 20

kHz.