Cím:	Megoldásvázlatok a 2009/4. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Gerõcs László
Füzet:	2009/május, 275 - 282. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Oldjuk meg a következő egyenletrendszert az egész számpárok halmazán: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 9^x\cdot 3^y}& {\displaystyle =\mathrm{81,}}\hfill \\ \hfill {\displaystyle 6x+6y+5xy}& {\displaystyle =0.}\hfill \end{array}}\}}\end{array}$  (11 pont)   Megoldás. Az első egyenletet $3^{2x+y}=3^4$ alakra hozzuk. Ekkor $2x+y=4$, azaz $y=4-2x$. Ezt helyettesítsük a második egyenletbe: $6x+6\left(4-2x\right)+5x\left(4-2x\right)=0$. Ebből az $5x^2-7x-12=0$ másodfokú egyenletet kapjuk. Ennek a megoldásai: $x_1=-1$, $x_2=\frac{12}{5}$. Mivel ez utóbbi nem egész szám, azért az egyenletrendszer megoldása az egész számpárok halmazán: $\left(x;y\right)=\left(-1;6\right)$.   2. Az $\mathrm{1,2,3,}\text{...}\mathrm{,}n$ pozitív egész számok felhasználásával halmazokat képeztünk az alábbi módon: ${\displaystyle \begin{array}{c}{\displaystyle \text{<span style="font-style: italic;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math> halmaz a páros számok halmaza;</span>}}\hfill \\ {\displaystyle \text{<span style="font-style: italic;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math> halmaz a <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn></math>-mal osztható számok halmaza;</span>}}\hfill \\ {\displaystyle \text{<span style="font-style: italic;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math> halmaz az <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn></math>-tel osztható számok halmaza.</span> }}\hfill \end{array}}$ $a)$ Véletlenszerűen kiválasztva egy számot az $n$ db szám közül, mekkora annak a valószínűsége, hogy azt nem használtuk fel a halmazok képzésekor, ha $n=48$?  (6 pont) $b)$ Ha az $A\cap B\cap C$ halmaznak $2$ eleme van, akkor hány eleme lehet az $\left(A\cap B\right)\setminus C$ halmaznak?  (7 pont)   Megoldás. $a)$ 1-től 48-ig azok a pozitív egész számok, melyek sem 2-vel, sem 3-mal, sem 5-tel nem oszthatók: 1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47. Tehát összesen 13 db ilyen szám van. Mivel az összes kiválasztási lehetőségek száma 48, így a keresett valószínűség: $\frac{13}{48}\approx 0\mathrm{,}271$. $b)$ Az $A\cap B\cap C$ halmazba azok az elemek vannak, melyek 2-vel, 3-mal és 5-tel is oszthatók, vagyis oszthatók 30-cal. Ha ennek a halmaznak 2 eleme van, akkor ezek az elemek csak a 30 és a 60 lehetnek. Így $n$ értéke legalább 60, de $n$ biztosan kisebb 90-nél, hiszen ellenkező esetben az $A\cap B\cap C$ halmaznak már 3 eleme lenne. Tehát: $60\le n<90$. Az $\left(A\cap B\right)\backslash C$ halmaznak azok a 2-vel és 3-mal is osztható (tehát 6-tal osztható) számok az elemei, melyek 5-tel nem oszthatók. Ha $n=60$, akkor 8 db ilyen szám van: 6, 12, 18, 24, 36, 42, 48, 54. Ha $n$ értékét növeljük a megengedett határig, akkor még 4 db ilyen számot találunk: 66, 72, 78, 84. Ezek szerint ha az $A\cap B\cap C$ halmaznak 2 eleme van, akkor az $\left(A\cap B\right)\backslash C$ halmaz számossága: $8\le |\left(A\cap B\right)\backslash C|\le 12$.   3. Egy szarvasmarha telepen $1000$ tehenet tartanak. Ezek egy évben $7300000$ liter tejet adnak. A telep vezetősége azt tapasztalta, hogy ‐ valószínűleg az egy marhára jutó legelőterület növekedése miatt ‐ ha a tehenek számát $5\%$-kal csökkentik, akkor az egy tehénre jutó éves tejhozam $10\%$-kal növekszik. $a)$ A tehenek számának $5\%$-os csökkentése esetén mennyivel növekszik az éves tejtermelés a gazdaságban?  (5 pont) $b)$ Ilyen állomány esetében az a tény, hogy a tehenek számának $p\%$-os csökkentésével egy tehén éves tejhozama $2p\%$-kal növekszik, csak $p<20$ esetén érvényes. Hány százalékkal kell csökkenteni a tehénállományt, hogy az éves tejtermelés $10\%$-kal növekedjen?  (8 pont)   Megoldás. $a)$ Egy tehén éves tejhozama $\frac{7300000}{1000}=7300$ liter. Ha a tehénállomány 5%-os csökkentésével az egy tehénre jutó éves átlagos tejhozam 10%-kal növekszik, akkor a gazdaságban az egy éves tejhozam: $1000\cdot 0\mathrm{,}95\cdot 7300\cdot 1\mathrm{,}1=7628500$. Tehát az éves tejhozam-növekedés: $7628500-7300000=328500$ liter. $b)$ A tehenek számának $p$%-os csökkentése után a tehenek száma: $1000\cdot \left(1-\frac{p}{100}\right)$. Az egy tehénre jutó éves $2p\%$-os növekedésével az egy tehénre jutó éves tejhozam: $\begin{array}{c}{\displaystyle 7300\cdot \left(1+\frac{2p}{100}\right)\mathrm{.}}\end{array}$ Ha a gazdaság ezzel éves szinten 10%-os növekedést ért el, akkor $\begin{array}{c}{\displaystyle 1000\cdot \left(1-\frac{p}{100}\right)\cdot 7300\cdot \left(1+\frac{2p}{100}\right)=7300000\cdot 1\mathrm{,}\mathrm{1,}}\end{array}$ amit $1+\frac{p}{100}-\frac{2p^2}{{100}^2}=1\mathrm{,}1$ alakban is írhatunk. Ebből: $p^2-50p+500=0$. A kapott egyenlet 20-nál kisebb gyöke: $p=25-5\sqrt[]{5}\approx 13\mathrm{,}8$. Tehát a tehénállomány kb. 13,8%-os csökkentésével az éves tejhozam 10%-kal növekedik.   4. A $p_1<p_2<p_3<p_4$ prímszámokról a következőket tudjuk: $p_3=p_1+p_2$, $p_2^2+8$ is prímszám és $p_4=2p_1{p}_2{p}_3+p_1+p_3$. Számítsuk ki a $p_1{p}_2{p}_3{p}_4$ szorzat értékét.  (14 pont)   Megoldás. Mivel a 2-n kívül minden prímszám páratlan, így a $p_3=p_1+p_2$ egyenlőségből következik, hogy a jobb oldali prímek valamelyikének párosnak kell lennie. Mivel a vizsgált prímek közül $p_1$ a legkisebb, azért csak $p_1=2$ lehet. Ha a $p_2=3k+1$ alakú, akkor $p_2^2=9k^2+6k+1$, így $p_2^2+8=9k^2+6k+9$, ami osztható 3-mal, így $p_2^2+8$ nem lenne prímszám. Ha a $p=3k+2$ alakú, akkor $p_2^2=9k^2+12k+4$, így $p_2^2+8=9k^2+12k+12$, ami osztható 3-mal, így $p_2^2+8$ nem lenne prímszám. Ezek szerint $p_2^2+8$ csak úgy lehet prímszám, ha $p$ osztható 3-mal, vagyis $p_2=3$. (Ekkor $p_2^2+8=9+8=17$, ami valóban prímszám.) Ezzel $p_3=p_1+p_2=5$, így $p_4=2p_1{p}_2{p}_3+p_1+p_3=2\cdot 2\cdot 3\cdot 5+2+5=67$. A keresett szám: $p_1{p}_2{p}_3{p}_4=2\cdot 3\cdot 5\cdot 67=2010$.   II. rész   5. A valós számok halmazán értelmezett $f\left(x\right)=x^3+p{x}^2+qx$ $\left(p\ne -\mathrm{2,}q\ne 0\right)$ függvényről tudjuk, hogy pontosan két zérushelye van, továbbá, hogy $f\left(2\right)=-p$. $a)$ Határozzuk meg a függvény zérushelyeit.  (8 pont) $b)$ Az $f\left(x\right)$ függvény origón átmenő érintője hol metszi a függvény görbéjét?  (8 pont)   Megoldás. $a)$ A feltételek szerint az $f\left(x\right)=x^3+p{x}^2+qx$ függvénynek pontosan két zérushelye van, azaz az $x^3+p{x}^2+qx=0$ egyenletnek pontosan két gyöke van. Emeljünk ki $x$-et a bal oldalon: $\begin{array}{c}{\displaystyle x\left(x^2+px+q\right)=0.}\end{array}$ Ez akkor és csak akkor teljesül, ha $x=0$, vagy $x^2+px+q=0$. Tehát az egyenlet egyik gyöke 0. Mivel az $x^2+px+q=0$ másodfokú egyenletnek csak egy gyöke lehet, azért a diszkriminánsa 0 kell, hogy legyen: $p^2-4q=0$. Azt is tudjuk, hogy $f\left(2\right)=-p$, tehát $f\left(2\right)=8+4p+2q=-p$, azaz $5p+2q=-8$. Az előző eredményből $4q=p^2$, azaz $2q=\frac{p^2}{2}$, így az utóbbi egyenlet: $5p+\frac{p^2}{2}=-8$, azaz $p^2+10p+16=0$, amiből: $p_1=-8$, $p_2=-2$. A feltételek szerint $p\ne -2$, így csak $p=-8$ lehet és ezzel $4q=64$, azaz $q=16$. Tehát a keresett függvény: $\begin{array}{c}{\displaystyle f\left(x\right)=x^3-8x^2+16x=x\left(x^2-8x+16\right)=x{\left(x-4\right)}^2\mathrm{.}}\end{array}$ A függvény zérushelyei: $x_1=0$, $x_2=4$. $b)$ Az origón átmenő érintő meredeksége az $f\left(x\right)$ függvénynek az $x=0$ helyen vett differenciálhányadosával egyenlő: $f\text{'}\left(x\right)=3x^2-16x+16$, ami $x=0$-ban 16. Tehát az érintő meredeksége 16, így az érintő egyenlete: $y=16x$. Ez az egyenes ott metszi az $f\left(x\right)$ függvényt, ahol $x^3-8x^2+16x=16x$, azaz $x^3-8x^2=0$, vagyis $x^2\left(x-8\right)=0$, ahonnan $x_1=0$, $x_2=8$. Tehát az $f\left(x\right)$ függvénynek az origóban húzott érintője a függvényt az $x=8$ helyen metszi.   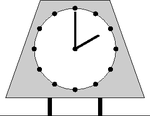6. Egy formatervező szimmetrikus trapéz alakú falemezre szerelt órát tervezett. Az óra körlapjának sugara 10 cm, középpontja a trapéz minden oldalától 12 cm távolságra van és a hosszabbik párhuzamos oldala a rövidebbnek kétszerese.     $a)$ Mekkora területű falemezre van szükség?  (7 pont) $b)$ $2$ óra után legközelebb mikor lesz a két óramutató hajlásszöge ugyanakkora, mint $2$-kor?  (9 pont)   Megoldás. $a)$ Képzeljük el, hogy az óra körlapját a középpontjából $\frac{12}{10}=\frac{6}{5}$ arányban nagyítjuk. Mivel a kör középpontja minden oldaltól 12 cm távolságra van, azért a nagyítás után a kapott kör érinteni fogja a trapéz minden oldalát. Ebből következik, hogy a trapéz érintőnégyszög.     Ha a trapéz rövidebb párhuzamos oldala $x$, akkor a hosszabb 2$x$, így az érintőnégyszögekre vonatkozó tétel alapján a szárai: $\frac{x+2x}{2}=\frac{3}{2}x$ hosszúak. A $BTC$ derékszögű háromszögben $BC=\frac{3}{2}x$, $BT=\frac{2x-x}{2}=\frac{1}{2}x$, $CT=m=2\cdot 12=24$. Írjuk fel a háromszögre Pitagorasz tételét: $\begin{array}{c}{\displaystyle {\left(\frac{3}{2}x\right)}^2={\left(\frac{1}{2}x\right)}^2+{24}^2\mathrm{,}\text{vagyis}\frac{9x^2}{4}=\frac{x^2}{4}+\mathrm{576,}}\end{array}$ ahonnan $x=12\sqrt[]{2}$. Ezzel a trapéz $T$ területe: $\begin{array}{c}{\displaystyle T=\frac{\left(24\sqrt[]{2}+12\sqrt[]{2}\right)\cdot 24}{2}=36\sqrt[]{2}\cdot 12\approx 610\mathrm{,}9.}\end{array}$ Kb. 610,9 cm${}^2$ területú falemezre van szükség egy óra elkészítéséhez. 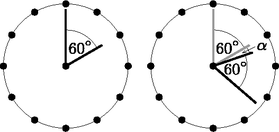$b)$ 2 órakor a kis- és nagymutató ${60}^{\circ }$-os szöget zár be egymással. Ha a kismutató $\alpha$ szöggel fordul el a legközelebbi olyan helyzetig, amikor a két mutató ismét ${60}^{\circ }$-os szöget zár be egymással, akkor a nagymutató ${60}^{\circ }+\alpha +{60}^{\circ }={120}^{\circ }+\alpha$ szöggel fordul el. Mivel a nagymutató forgási sebessége a kismutató forgási sebességének 12-szerese, azért $12\alpha ={120}^{\circ }+\alpha$, azaz $11\alpha ={120}^{\circ }$, ahonnan $\alpha =\frac{{120}^{\circ }}{11}$.     Most azt kell kiszámítanunk, hogy a kismutató $\alpha =\frac{{120}^{\circ }}{11}$ fokos elfordulása mennyi időt vesz igénybe. A kismutató 1 óra, azaz 60 perc alatt ${30}^{\circ }$-ot fordul el, így $1^{\circ }$-os elfordulás 2 percig tart. Ezek szerint az $\alpha$ szögű elfordulás $2\alpha$ percet vesz igénybe. Esetünkben az elfordulás ideje: $\begin{array}{c}{\displaystyle 2\cdot \frac{120}{11}=\frac{240}{11}\approx 21\mathrm{,}8\text{ perc.}}\end{array}$ Tehát 2 óra után legközelebb a két mutató kb. 2 óra 21 perc és 48 másodperckor zár be egymással ${60}^{\circ }$-os szöget.   7. Egy városi állatkertben a $4$ ragadozót (egy nőstény tigrist, egy oroszlánt, egy leopárdot és egy jaguárt) $8$ egymás melletti ketrecben helyezték el. $a)$ Hányféleképpen helyezhették el a ragadozókat a $8$ ketrecben?  (4 pont) $b)$ Az állatgondozók azt tapasztalták, hogy ha két ragadozó szomszédos ketrecbe kerül, akkor azok rendkívül agresszívekké válnak. Hányféleképpen helyezhették el a ragadozókat a $8$ ketrecben úgy, hogy szomszédos ketrecekbe ne kerüljenek állatok?  (5 pont) $c)$ A jaguárt elszállították, és hoztak helyébe egy hím tigrist. Annak érdekében, hogy a nőstény és a hím tigris ,,közeledjenek'' egymáshoz, e két tigrist szomszédos ketrecbe akarták elhelyezni. Ekkor hányféleképpen helyezhették el a ragadozókat, ha a két tigris szomszédos ketrecbe került, de ezen kívül nem voltak szomszédos ragadozók?  (7 pont)   Megoldás. $a)$ A 4 ketrecet, melyekbe elhelyezzük a ragadozókat $\left(\genfrac{}{}{0ex}{}{8}{4}\right)$-féleképpen választhatjuk ki. E lehetőségek közül bármelyiket kiválasztva, a kiválasztott 4 ketrecbe a 4 állat $4!$-féleképpen helyezhető el. Ezek szerint a ragadozókat a 8 db ketrecbe összesen $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{8}{4}\right)\cdot 4!=\frac{8!}{4!\cdot 4!}\cdot 4!=\frac{8!}{4!}=5\cdot 6\cdot 7\cdot 8=1680}\end{array}$ féle módon helyezhették el. $b)$ Számoljuk össze azokat az elhelyezési lehetőségeket, amikor szomszédos ketrecekben nincsenek állatok. 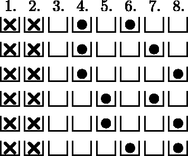Ha az 1. ketrecbe helyeztünk állatot, akkor helyezhetünk a 3., 5., 7. ketrecbe, vagy a 3., 5., 8. ketrecbe vagy a 3., 6., 8. ketrecbe vagy pedig a 4., 6. és 8. ketrecbe. Ha az első ketrecbe nem helyeztünk, akkor csak a 2., 4., 6. és 8. ketrecbe helyezhettünk állatot. Ez tehát öt lehetőség. Minden lehetőség $4!$-féleképpen valósulhat meg, hiszen az adott négy ketrecbe az állatok $4!$-féleképpen helyezhetők. Ezek szerint a 4 állatot úgy elhelyezni a 8 ketrecben, hogy ne legyenek szomszédok, összesen $5\cdot 4!=120$-féleképpen lehetséges. 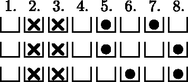$c)$ Ismét számoljuk össze a lehetőségeket. A két tigris lehet az 1‐2. vagy 2‐3. vagy 3‐4. vagy 4‐5. vagy 5‐6. vagy 6‐7. vagy 7‐8. ketrecben. Ha az 1‐2. ketrecben vannak a tigrisek, akkor 6 lehetőség van.     Mivel a két tigris is és a másik két ragadozó is kétféleképpen foglalhatja el a helyét, azért ez esetben a lehetőségek száma: $6\cdot 2\cdot 2=24$. Ha a két tigris a 2‐3. ketrecben van, akkor 3 lehetőség van.     Ekkor az állatokat $3\cdot 2\cdot 2=12$-féleképpen helyezhetik el a kívánt módon. Ha a két tigris a 3‐4. ketrecbe kerül, akkor 4 eset van.     Ekkor a lehetőségek száma: $4\cdot 2\cdot 2=16$. Ugyancsak 4-féleképpen választhatók ki a ketrecek, ha a tigrisek a 4‐5. helyen vannak.     Tehát ez esetben is 16-féleképpen helyezhetők el az állatok a feltételeknek megfelelően. A szimmetria-okok miatt az 5‐6. eset megegyezik a 3‐4. esettel, a 6‐7. eset megegyezik a 2‐3. esettel, végül a 7‐8. eset megegyezik az 1‐2. esettel. Ezek szerint a 4 ragadozót a 8 ketrecben úgy elhelyezni, hogy a tigrisek szomszédos ketrecben legyenek, de ezen kívül ne legyenek szomszédos ragadozók, összesen $\begin{array}{c}{\displaystyle 24+12+16+16+16+12+24=120}\end{array}$ féle módon lehet.   8. Egy négyzet alapú ház tetőszerkezete négyzet alapú egyenes gúla. Az oldalélek az alapnégyzettel ${36}^{\circ }$-os szöget zárnak be.     $a)$ Számítsuk ki a tetőszerkezet oldallapjának és alaplapjának a hajlásszögét.  (3 pont) $b)$ Mekkora a tetőszerkezet légtere, ha az oldaléle 8 m hosszú?  (4 pont) $c)$ A tetőszerkezet alapnégyzetét ereszcsatorna veszi körül. A lehulló eső a tetőről az ereszcsatornába, onnan pedig a ház egyik sarkánál függőlegesen haladó csatornán keresztül az alá helyezett egyenes körhenger alakú hordóba folyik. A hordó átmérője 68 cm, magassága 120 cm. Egy $15$ percig tartó nyári felhőszakadás során a híradások szerint 20 mm csapadék hullott óránként. Megtelik-e a felhőszakadás után a tetőről lefolyt vízzel a hordó?  (9 pont)   Megoldás. $a)$ Legyen a tetőtér alapnégyzetének oldala $a$, magassága $m$; az oldallap és az alaplap hajlásszögét az ábrán $\alpha$-val jelöltük.     Az $ATE$ derékszögű háromszögben: $\begin{array}{c}{\displaystyle AT=\frac{a\sqrt[]{2}}{2}\mathrm{,}\text{így}\text{tg}{36}^{\circ }=\frac{m}{\frac{a\sqrt[]{2}}{2}}=\frac{m\sqrt[]{2}}{a}\mathrm{.}}\end{array}$ Az $EFT$ derékszögű háromszögben: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{m}{\frac{a}{2}}=\frac{2m}{a}\mathrm{.}}\end{array}$ Ezt és az előbb kapott eredményt elosztva egymással azt kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{\text{tg}\alpha }{\text{tg}{36}^{\circ }}=\frac{\frac{2m}{a}}{\frac{m\sqrt[]{2}}{a}}=\frac{2}{\sqrt[]{2}}=\sqrt[]{2}\mathrm{,}\text{azaz}\text{tg}\alpha =\sqrt[]{2}\cdot \text{tg}{36}^{\circ }\mathrm{,}\text{ahonnan}\alpha \approx 45\mathrm{,}{78}^{\circ }\mathrm{.}}\end{array}$ Ha tehát a négyzet alapú egyenes gúla oldaléle az alaplappal ${36}^{\circ }$-os szöget zár be, akkor az oldallap az alaplappal kb. $45\mathrm{,}{78}^{\circ }$-os szöget zár be. $b)$ Ha a gúla oldaléle 8, akkor az $ATE$ háromszögből $\begin{array}{c}{\displaystyle \text{cos}{36}^{\circ }=\frac{AT}{8}\mathrm{,}\text{ahonnan}AT=8\cdot \text{cos}{36}^{\circ }\approx 6\mathrm{,}47\text{m. }}\end{array}$ Az $AT$ ismeretében az alapnégyzet oldala: $a\approx 9\mathrm{,}15$ m. A gúla $m$ magasságára $\text{sin}{36}^{\circ }=\frac{m}{8}$, ahonnan $m=8\cdot \text{sin}{36}^{\circ }\approx 4\mathrm{,}70$ m. A gúla $V$ térfogata, vagyis a tetőtér légtere: $\begin{array}{c}{\displaystyle V=\frac{a^{2}m}{3}=\frac{9\mathrm{,}{15}^2\cdot 4\mathrm{,}7}{3}\approx 131\mathrm{,}17\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>. }}\end{array}$ $c)$ A hordó sugara 0,34 m, magassága 1,2 m. Tehát a hordó $V_{\text{h}}$ térfogata: $\begin{array}{c}{\displaystyle V_{\text{h}}=r^2\pi \cdot m=0\mathrm{,}{34}^2\pi \cdot 1\mathrm{,}2\approx 0\mathrm{,}4358\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>. }}\end{array}$ Ha a kérdéses felhőszakadás alkalmával 20 mm csapadék esett óránként, akkor 15 perc alatt 5 mm. A tetőre hulló csapadék egy 9,15 m oldalú négyzetre eső csapadéknak felel meg, tehát a tetőre hulló csapadék térfogata egy olyan négyzetes hasáb térfogatával egyezik meg, melynek alapnégyzete 9,15 m, magassága pedig 5 mm, azaz 0,005 m. Ennek térfogata: $9\mathrm{,}{15}^2\cdot 0\mathrm{,}005\approx 0\mathrm{,}4186\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$. Mivel a hordó térfogata 0,4358 m${}^3$, így a tetőről lefolyó csapadékkal nem telik meg a hordó.   9. $a)$ Egy pedagógiai konferencia középiskolai szekciójába $12$ fő jelentkezett. A $12$ fős csoport két tagja (a moderátorok) a csoportból mindenkit ismertek. Öt olyan tagja volt a csoportnak, akik a moderátorokon kívül senkit sem ismertek; a szekció többi tagja közül pedig mindenki mindenkit ismert (az ismeretség minden esetben kölcsönös). Az első szekcióülés előtt, akik nem ismerték egymást, kézfogással bemutatkoztak egymásnak. Hány kézfogás történt?  (7 pont) $b)$ Az óvodai szekciónak három moderátora volt; ők szintén mindenkit ismertek a csoportból. A csoport többi tagjának a fele a moderátorokon kívül senkit sem ismert, míg a csoport többi tagja közül itt is mindenki mindenkit ismert (természetesen az ismeretség itt is minden esetben kölcsönös). Ebben a szekcióban is bemutatkoztak egymásnak azok, akik nem ismerték egymást, s így ebben a csoportban $35$ kézfogásra került sor. Hány főből állt az óvodai szekció?  (9 pont)   Megoldás. $a)$ Készítsük el a 12 fős társaság ismeretségi gráfját. Legyenek $A$ és $B$ a moderátorok, $C$, $D$, $E$, $F$ és $G$ azok a személyek, akik a moderátorokon kívül senki mást nem ismertek; a többiek pedig $H$, $I$, $J$, $K$ és $L$.     Azt kell meghatároznunk, hogy e gráfba hány élt kellene még berajzolnunk, hogy teljes gráfot kapjunk. Az $A$ és $B$ pontok fokszáma 11-11. A $C$, $D$, $E$, $F$ és $G$ pontok mindegyikének fokszáma 2. A $H$, $I$, $J$, $K$ és $L$ pontok mindegyikének fokszáma 6. Így a gráfban a fokszámok összege: $2\cdot 11+5\cdot 2+5\cdot 6=62$, vagyis a gráf jelenleg meglevő éleinek a száma 31. Mivel a 12 pontú teljes gráf éleinek a száma $\frac{12\cdot 11}{2}=66$, és jelenleg 31 éle van, így a hiányzó élek száma 35. Tehát a szekcióülés előtt 35 kézfogásra került sor. $b)$ Legyen $A$, $B$, $C$ a három moderátor. Legyen $k$ db olyan személy, akik a moderátoron kívül senkit sem ismertek. Ekkor a csoport többi tagjai (ugyancsak $k$ db személy) közül mindenki mindenkit ismert. Ekkor a gráfnak $2k+3$ pontja van.     A három moderátor és azok, akik közül mindenki mindenkit ismert, együtt egy $k+3$ pontú teljes gráfot alkotnak, amiben $\frac{\left(k+3\right)\left(k+2\right)}{2}$ él van. Azok a személyek, akik csak a moderátorokat ismerték, $3k$ élt jelentenek, így a gráf meglevő éleinek a száma: $\frac{\left(k+3\right)\left(k+2\right)}{2}+3k$. A $2k+3$ pontú teljes gráf éleinek a száma: $\begin{array}{c}{\displaystyle \frac{\left(2k+3\right)\left(2k+2\right)}{2}\mathrm{,}}\end{array}$ így a meglevő gráf hiányzó éleinek a száma: $\begin{array}{c}{\displaystyle \frac{\left(2k+3\right)\left(2k+2\right)}{2}-\frac{\left(k+3\right)\left(k+2\right)}{2}-3k=\mathrm{35,}}\end{array}$ ami $4k^2+10k+6-k^2-5k-6-6k=70$ alakban is írható. Vagyis a $3k^2-k-70=0$ másodfokú egyenletet kaptuk. A negatív megoldás nyilván érdektelen, így $k=5$. Tehát az óvodai szekciónak $2k+3=13$ tagja volt.