Kezdőlap


Cím:	Delta-kommandó, avagy rekurziók és differencia-egyenletek
Szerző(k):	Kós Rita
Füzet:	2009/május, 260 - 267. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alapfeladat. A Nagyáruház előtti parkolóban szeretnénk parkolóhelyet találni lehetőleg minél közelebb a bejárathoz úgy, hogy nem tudva, vannak-e még a bejáratig üres helyek, a parkolóhelyek mellett haladva eldönthetjük, hogy beállunk-e az üres helyre vagy továbbmegyünk. Ha továbbmentünk, vissza már nem fordulhatunk. Mindezt a folyamatot a lehető legrövidebb idő alatt akarjuk végrehajtani. Mi a legjobb stratégia?

Cikkünkben igyekszünk behatolni abba a szemléletmódba, amikor egy folyamatot adott pillanatokban feljegyzett állapotának változásával/változásaival, vagy néhány, egymást követő állapot egymáshoz való viszonyának segítségével (rekurzió) írjuk le. Például a bankszámlámon tartott pénzem kamatozik, mely kamatot a bank naponta jóváírja: ha ma

f_{0} = 10 000

Ft-om van, a napi kamat 0,02%, akkor holnap

f_{1} = f_{0} \cdot 1, 0002 = 10 002

Ft-om lesz (rekurzió). Másként megfogalmazva, a pénzem naponta az előző napi összeg 0,0002-szeresével nő:

f_{1} - f_{0} = 0, 0002 f_{0}

(differencia-egyenlet). Azaz a kezdeti lépéseket kívánjuk megtenni a felé, hogy a differencia-egyenlettel megadott folyamatok állapotait ki tudjuk számolni egyszerűbb esetekben közvetlenül ‐ az egyenlet megoldásával; példánkban megmondhatjuk, hogy két hét múlva mennyi pénzünk lesz (

f_{13} = f_{0} \cdot 1, 0002^{13} = 10 026

Ft).
Egy folyamat azonos időközönként mért állapotait jelöljük

s_{k}

-val (

k = 0,1,2, ...

), például jódizotópok számát a megfigyelés kezdetétől eltelt

k

-adik napon. Legyen a differencia, azaz változás jele

Δ

{(Δ s)}_{k} = s_{k + 1} - s_{k}

. A változás változását, majd azok változását stb. is értelmezhetjük, így

n

-ed rendű differenciának nevezzük azt az

s

-ből képzett

Δ^{n} s

sorozatot, amelynek

k

-adik tagja

\begin{matrix} {(Δ^{n} s)}_{k} = {(Δ^{n - 1} s)}_{k + 1} - {(Δ^{n - 1} s)}_{k} . \end{matrix}

1. Delta 1

A legegyszerűbb egyenlet a jó öreg számtani sorozatról szól:

\begin{matrix} {(Δ s)}_{k} = s_{k + 1} - s_{k} = d, \end{matrix}

(1)

ahol

d

egy adott szám. Ha

d = 0

, akkor a sorozat konstans-sorozat. Ha

d \neq 0

, akkor az egyenlet megoldása:

s_{k} = s_{0} + k \cdot d

. Általánosíthatjuk is (1)-et például az

\begin{matrix} α s_{k + 1} - β s_{k} = γ \end{matrix}

egyenletre, ami picit más alakban írva:

\begin{matrix} α (s_{k + 1} - s_{k}) + (α - β) s_{k} = γ \end{matrix}

(

α

β

γ

adott számok). Ezekben az egyszerű esetekben célszerű a sorozat első néhány tagjának felírásával megsejteni a tetszőleges

k

-adik tagra vonatkozó képletet.

1. feladat. Szeretném a 2 m hosszú, 2 cm vastagra lapított hálózsákomat összegöngyölve belepréselni a zsákjába. Belefér-e, ha a (henger alakú) zsák keresztmetszetének átmérője 22 cm?

Amíg az együtthatók adott konstansok és

γ = 0

, a feladatok ebben és a későbbi fejezetekben is megoldhatóak a lineáris rekurzív sorozatok elméletének segítségével (l. a 2.1. fejezetben).
Írjuk föl differenciával az első általánosítást:

\begin{matrix} Δ s = (q - 1) s + c, \end{matrix}

(2)

ahol

\frac{β}{α} : = q

és

\frac{γ}{α} : = c

(

α \neq 0

).
A

γ = c = 0

esetben ismét egy ismerőssel találkozunk:

\begin{matrix} s_{k + 1} = s_{k} + Δ s_{k} = q \cdot s_{k} = s_{0} \cdot q^{k + 1} \end{matrix}

mértani sorozat ‐ pénzügyi szemmel pedig az, ha a számlánkra betett pénz azonos időközönként mindig ugyanannyival kamatozik.

2. feladat. Egy kémcsőnyi víz

^{131} J

jódizotóppal szennyeződött be.

4

nappal később a kémcső tartalmának aktivitása 185 Bq volt. Hány gramm

^{131} J

került a vízbe? (

1 Bq=1

bomlás másodpercenként, 1 g

^{131} J

-nak az aktivitása

4, 6 \cdot 10^{15} Bq

, a felezési idő 8 nap.)

c \neq 0

, akkor

s_{k + 1} = q \cdot s_{k} + c

-re azt a gyakorlati példát is mondhatjuk, hogy minden időegység alatt mindig adott összeget vonnak le kezelési költségként/mindig ugyanannyit teszünk be a számlára. Ezért itt már két helyen is van mértani sorozat: az egyik pont az előző, a másik pedig ugyanazon kvóciensű (hányadosú) sorozat tagjainak összege, ahol az első tag

c

. Így

\begin{matrix} s_{k} = s_{0} \cdot q^{k} + \frac{q^{k} - 1}{q - 1} c, \end{matrix}

amiből az exponenciális tagot kiemelve

\begin{matrix} s_{k} = (\frac{c}{q - 1} + s_{0}) \cdot q^{k} - \frac{c}{q - 1} . \end{matrix}

(3)

3. feladat. Igazoljuk a képletet! Mi történik az

α = 0

és az

α = β

esetekben?

4. feladat. Minden újszülött jogosult százezer forintnyi babakötvényre, amit a Magyar Államkincstár állít ki. Egy lelkes fiatal házaspár elhatározza, hogy minden hónapban ötezer forintot tesznek be Emma lányuk számlájára, amíg

18

éves nem lesz. Arra számítanak, hogy évi

10 %

-os kamat mellett szép summa gyűlik majd össze. Vajon fedezi-e Emma egyetemi tanulmányait az így felhalmozott összeg?

γ = c = 0

eset egy lineáris rekurzió (l. a 2.1. fejezetet), a leíró egyenletet pedig homogénnek nevezik. (Egy egyenlet homogén, ha megoldáshalmaza megegyezik tetszőleges

λ \neq 0

-szorosának megoldáshalmazával. Egy

f

függvény homogén, ha tetszőleges

λ \neq 0

-val

\begin{matrix} f (x_{1}, x_{2}, ..., x_{n}) = λ f (\frac{x_{1}}{λ}, \frac{x_{2}}{λ}, ..., \frac{x_{n}}{λ}) . \end{matrix}

Egy koordinátarendszer homogén, ha tetszőleges

λ \neq 0

-ra az

(x_{1}, x_{2}, ..., x_{n})

és a

(λ x_{1}, λ x_{2}, ..., λ x_{n})

koordináták ugyanazt a pontot jelölik.) A homogén egyenlet megoldását jelöljük

s^{h}

-val. Ha

c \neq 0

, akkor az egyenlet már nem homogén, azaz inhomogén. Nem nehéz észrevenni, hogy (ha

q \neq 1

) az

s = \frac{c}{1 - q}

konstans sorozat a megoldása a (2) egyenletnek, jelöljük ezt

s_{p}^{i h}

-vel¹. A

q = 1

esetről a 4. feladat szólt. Ugyanakkor tetszőleges

A

valós számmal az

\begin{matrix} s^{i h} = s_{p}^{i h} + A \cdot s^{h} \end{matrix}

(4)

megoldásokat tudjuk előállítani.
Fontos megjegyezni, hogy ha az

{s_{0}, s_{1}, ...}

sorozat megoldása egy

d

differencia-egyenletnek, akkor

{s_{i}, s_{i + 1}, ...}

i = 1,2, ...

is megoldása. Másrészről, ha az egyenletnek több sorozat is eleget tesz, akkor az előzőek értelmében bármely két megoldás-sorozat esetén vagy az egyik tartalmazza a másikat, vagy nincs közös elemük; ezt úgy is szokás mondani, hogy a megoldások nem keresztezik egymást és nem ágaznak el.

5. feladat. Bizonyítsuk be a fenti állítást!

Általában, ha

d

egy adott problémát, folyamatot ír le, akkor a feladat tartalmaz konkrét (kontroll) feltételeket, peremfeltételeket (pl. a repülő sebessége, amiből az ejtőernyősök kiugrottak,

v_{0}

volt).
Így az iménti megoldás folytatható a peremfeltételhez való igazítással:

\begin{matrix} A = \frac{c}{q - 1} + s_{0}, \end{matrix}

amivel visszakapjuk a korábbi megoldásban adódott (3) sorozatot.

2. Delta 2

A Fibonacci-számok (általánosabban pedig a Fibonacci-féle sorozatok²) megadásában három egymást követő sorozat-elem szerepel:

f_{k} + f_{k + 1} = f_{k + 2}

, illetve általában

α f_{k} + β f_{k + 1} = f_{k + 2}

. Ebben az esetben azt is mondhatjuk, hogy a különbségek különbsége áll az egyenlet egyik oldalán. Ugyanis

\begin{matrix} {(Δ^{2} f)}_{k} = {(Δ f)}_{k + 1} - {(Δ f)}_{k} = f_{k + 2} - 2 f_{k + 1} + f_{k} \end{matrix}

jelöléssel a Fibonacci sorozat megadható egy differencia-egyenlet megoldásaként:

Δ^{2} f + Δ f - f = 0

. Az egyenlet megoldása ismert:

\begin{matrix} f_{k} = A {(\frac{1 + \sqrt[]{5}}{2})}^{k} + B {(\frac{1 - \sqrt[]{5}}{2})}^{k} . \end{matrix}

A klasszikus esetben

f_{0} = 0

és

f_{1} = 1

a kezdőfeltételek, melyekkel

A = - B = \frac{\sqrt[]{5}}{5}

6. feladat. Az első rész eredményeit felhasználva oldjuk meg a

\begin{matrix} Δ^{2} f + (1 - r) Δ f = 0 \end{matrix}

másodrendű egyenletet, ha

f_{1} = c + r \cdot f_{0}

, ahol

c

a feladathoz adott konstans.

2.1. Delta

n

A legegyszerűbb homogén differencia-egyenletek lineáris rekurziók, ezért hasznos, sőt szükséges az ismeretük ‐ gondoljunk csak a (4)-beli elvre.
Az

\begin{matrix} a_{0} r_{k} + a_{1} r_{k - 1} + a_{2} r_{k - 2} + ... + a_{n - 1} r_{k - n + 1} + a_{n} r_{k - n} = 0 \end{matrix}

rekurzió (

a_{i} \in R

i = 1,2, ... n

) megoldásának első lépése az

\begin{matrix} a_{0} x^{n} + a_{1} x^{n - 1} + ... + a_{n - 1} x + a_{n} \end{matrix}

karakterisztikus polinom felírása. Tegyük fel, hogy ennek az egymástól különböző gyökei

q_{1}, q_{2}, ... q_{j}

j \leq n

. Ha

j = n

, akkor a sorozat tagjai

\begin{matrix} r_{k} = A_{1} q_{1}^{k} + ... + A_{n} q_{n}^{k} \end{matrix}

(5)

alakban állnak elő. (Ha valamelyik gyök nem valós komplex szám, akkor az együtthatója is az.)

7. feladat. Igazoljuk az állítást.

Abban az esetben, ha pl.

q_{1}

többszörös gyök, azaz

{(x - q_{1})}^{ℓ}

osztója a karakterisztikus polinomnak (

2 \leq ℓ \leq n - j + 1

), akkor az (5)-beli összegben

ℓ

darab tagot az

A_{1} q_{1}^{k} + A_{2} k q_{1}^{k} + ... + A_{ℓ} k^{ℓ - 1} q_{1}^{k}

összeg helyettesít. Így az általános megoldás (5)-nél bonyolultabb:

\begin{matrix} \sum_{i}^{} a_{i} (k) q_{i}^{k}, \end{matrix}

ahol

a_{i}

egy olyan polinom, amelynek a foka kisebb, mint a

q_{i}

gyöknek a multiplicitása.

Speciálisan a másodrendű esetben (azaz ha

n = 2

) a karakterisztikus polinom gyökeiként kaphatunk két különböző valós számot (mint például a Fibonacci-sorozat esetében is), és

s_{k}^{h} = A_{1} q_{1}^{k} + A_{2} q_{2}^{k}

. Előfordulhat, hogy a karakterisztikus polinom ,,teljes négyzet'', azaz egy gyöke van (ami kétszeres). Ebben az esetben

\begin{matrix} s_{k}^{h} = A_{1} q^{k} + A_{2} k q^{k} . \end{matrix}

8. feladat. Mutassuk meg, hogy a karakterisztikus polinom

a)

egyik gyöke pontosan akkor

1

, ha a differencia-egyenlet visszavezethető egy elsőrendű egyenletre;

b)

pontosan akkor ,,teljes négyzet'', ha a differencia-egyenlet is az.

Harmadik esetként, ha a karakterisztikus polinomnak két (egymással konjugált) nem valós komplex gyöke van, akkor az

A_{1}

és

A_{2}

együtthatók olyan komplex számok, amelyek egymás konjugáltjai.
Az elméletet azonban óvatosan kell alkalmazni a gyakorlatban!

1. példa. Régen a magasfeszültséget szállító vezetékek mellett porcelántárcsákat használtak szigetelésnek. Ezt úgy kellett megtervezni, hogy sehol se üssön át.

Ezt az áramkört sematikusan egy létraszerű nagyon-nagyon hosszú kondenzátorsorral lehet szemléltetni: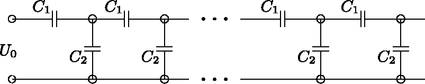

k

-adik csomópontban a feltétel szerint

\sum Q = 0

, így felírható a

\begin{matrix} C_{1} U_{k + 1} - (2 C_{1} - C_{2}) U_{k} + C_{1} U_{k - 1} = 0 \end{matrix}

rekurzió. A karakterisztikus polinom szerint van megoldás, ha

C_{2} \geq 4 C_{1}

, ám a tapasztalatok szerint

U_{k} = U_{0} \cdot q^{k}

alakú (ahol

q

a nagyobbik gyök).

1. gyakorlat. A

C_{2} \geq 4 C_{1}

esetben számítsuk ki

q

értékét.

3. Delta 1 ‐ P kód

Modellezzük az Alapfeladatot a lehető legegyszerűbb esetre. A parkolóhelyek egymás után vannak sorban, az áruháztól való távolságuk növekvő sorrendjében számozva. Csak az éppen mellettünk levő parkolóról látjuk, hogy foglalt-e vagy sem ‐ meg persze a már mögöttünk levőkről. Legyen

p

annak a valószínűsége, hogy egy hely szabad,

q = 1 - p

pedig annak, hogy foglalt; minderről pl. a bejáratnál levő számláló tájékoztathat, és ez a parkolás ideje alatt nem változik.

3.1. P1

A feladatbeli feltételeket modellezhetjük azzal, hogy a kevésbé jó parkolást büntetjük. A parkolásért annyit kelljen fizetni, amilyen messze van a hely (

k

), de ha nem állunk meg, és az áruház elé érünk (0. hely), akkor igen magas összegre rúgó büntetést kapunk (

C

). Ezzel az átfogalmazással a lehető legkisebb díjat keressük. A következő kérdésre kell tehát válaszolni: mikor döntünk úgy, hogy a következő szabad helyre beállunk?
A

k

-adik helynél állva azt mérlegeljük: ha szabad, akkor leparkolunk, és a fizetendő díj

k

, vagy előre megyünk eggyel. Azt választjuk, ami jobban megéri:

k

és

V_{k - 1}

közül melyik a kisebb, ha általában

V_{n}

-nel jelöljük a várhatóan fizetendő összeget az

n

-edik helyen. Ha foglalt a hely, akkor muszáj továbbállni. Ezért

\begin{matrix} V_{k} = p \cdot {min}_{}^{} {k, V_{k - 1}} + q \cdot V_{k - 1} . \end{matrix}

(6)

Ez a várható tarifa az áruház felé haladva sajnos nem csökken (különben gondolkodás nélkül előrehajtanánk). A rekurzió felírásakor természetesnek vettük, hogy a (

k - 1

)-edik helyen is ugyanezt a stratégiát fogjuk követni. Ez egy nagyon fontos elv az optimalizációs és kontroll folyamatok vizsgálatánál: a legjobb stratégia meghatározásához (pl. optimális gazdasági növekedés, befektetések, monetáris és fiskális politika), amit Bellmann-elvként/egyenletként³ ismernek. A lényege: az optimális stratégia minden lépése optimális.

9. feladat. Mutassuk meg, hogy

V_{k}

nemnövő sorozat.

Tehát amíg

k \geq V_{k - 1}

, addig haladunk előre, és

V_{k} = V_{k - 1}

. Abban a pillanatban, amikor

k \leq V_{k - 1}

, azaz

V_{k} = p k + q \cdot V_{k - 1}

a várható díj ‐ a legelső szabad helyre beállunk. Ahogy az első részben, itt is egy lehetséges megoldás

V_{0}, V_{1}, V_{2}, ...

felírásával megsejteni

V_{k}

alakját és indukcióval bizonyítani. Ehelyett azonban nézzük a megoldandó differencia-egyenletet:

\begin{matrix} Δ V + p V = p k + p . \end{matrix}

(7)

Általánosabban, vizsgáljuk a

\begin{matrix} Δ V = μ V + ν k + ω \end{matrix}

(8)

differencia-egyenletet. Tudjuk, hogy a speciális

ν = 0

és

ω = 0

(homogén) esetben a (3) szerint

V_{k}^{h} = V_{0}^{h} {(μ + 1)}^{k}

10. feladat. Mi a megoldása a

Δ V = 2 k + 1

egyenletnek? És a

Δ V = ν k + ω

-nak?

A (4) szerint keressünk a (8) kérdésre egy konkrét

V_{k}^{*}

megoldást, mert akkor a

V_{k} = A \cdot V_{k}^{h} + V_{k}^{*}

-ként előállított is jó (

A

tetszőleges szám). Márpedig

\begin{matrix} V_{k}^{*} = - \frac{ν}{μ} k - \frac{ν}{μ^{2}} - \frac{ω}{μ}, (μ \neq 0), illetve V_{k}^{*} = \frac{ν}{2} k^{2} + (ω - \frac{ν}{2}) k, (μ = 0), \end{matrix}

ezt visszahelyettesítve egyenlőséget kapunk! Így a megoldás, természetesen igazítva az adott sorozathoz:

\begin{matrix} V_{k} = \frac{V_{0} + \frac{ν}{μ^{2}} + \frac{ω}{μ}}{V_{0}^{h}} {(μ + 1)}^{k} - \frac{ν}{μ} k - \frac{ν}{μ^{2}} - \frac{ω}{μ}, illetve V_{k} = \frac{ν}{2} k^{2} + (ω - \frac{ν}{2}) k + V_{0} . \end{matrix}

Alkalmazzuk

μ = - p

ν = p

ω = p

és

V_{0} = C

-re, hogy megkapjuk a várható parkolási díj nagyságát:

\begin{matrix} V_{k} = (C + \frac{q}{p}) q^{k} + k - \frac{q}{p} . \end{matrix}

Némi számolás után kiderül, hogy a kritikus hely

k_{0} = [1 - log_{q} (p C + q)] + 1

(

[x] = n

, ahol

n \leq x < n + 1

n \in N

). Ha valóban alkalmazni szeretnénk ezt a stratégiát, akkor

C

megválasztásával tudjuk biztosítani, hogy elég nagy valószínűséggel valóban le tudjunk parkolni, de ne kelljen túl messze megállni csak azért, mert ,,biztosra'' akarunk menni.

11. feladat. Mi annak a valószínűsége, hogy a kiszámolt

k_{0}

-adik parkolóhely után mégsem lesz szabad hely?

12. feladat. Hogyan válasszuk meg

C

-t, ha legalább

90 %

-os eséllyel szeretnénk üres helyet találni?

3.2. P2

Befejezésül néhány megjegyzés a feladat modelljének egy kissé módosított változatáról. Annak a valószínűsége, hogy a

k

-adik hely foglalt, legyen a hely függvénye

q : N \to (0,1)

, például

q (k) = q^{k}

. Ekkor a megoldandó egyenlet

\begin{matrix} Δ V + \frac{1 - q^{k}}{q^{k}} \cdot V = \frac{1 - q^{k}}{q^{k}} \cdot k, \end{matrix}

(9)

ennek megoldásához a korábban megbeszéltekből két dolog használható. Elmondható ugyanis, hogy ha van megoldás, akkor adott

V_{0}

kezdőfeltétel esetén ez egyértelmű. Másrészről ha

V_{k}^{h}

megoldása a

\begin{matrix} Δ V + \frac{1 - q^{k}}{q^{k}} \cdot V = 0 \end{matrix}

(10)

homogén egyenletnek,

V_{k}^{*}

pedig egy konkrét (általános) megoldás, akkor

V_{k} = A \cdot V_{k}^{h} + V_{k}^{*}

is megoldása (9)-nek. Látjuk, hogy (10) már nem lineáris, nem használhatjuk azt, ami idáig jól működött. Célunk ugyanakkor a módosított probléma megoldása, azaz a

V_{k} \leq k

egyenlőtlenség küszöbindexének megtalálása: a legelső jó

k

, amit nevezzünk

k_{0}

-nak. Adott

C

és

q

mellett ez persze megállapítható, általános megoldáshoz pedig használhatunk egy

V_{k}

-t közelítő megoldást:

\begin{matrix} \tilde{V_{k}} = (C + 1) q^{\frac{k^{2}}{2}} + k - 1, \end{matrix}

aminek segítségével

\begin{matrix} k_{0} = ⌈ \sqrt[]{log_{q} C} ⌉ . \end{matrix}

(

⌈ x ⌉ = [x] + 1

, az

x

felső egészrésze.)

13. feladat. Mutassuk meg, hogy a

\tilde{V_{k}}

közelítő megoldás minimumhelye

k_{0}

és

| {\tilde{V}}_{k_{0}} - k_{0} | < 1

Ez lesz a munkamódszere a differenciál-egyenletek megoldásának is (pl. mi történik a villany felkapcsolásakor, miért kering ellipszis pályán a Föld). A történet pedig ott folytatódik.

Felhasznált irodalom

[1]	http://www.math.bme.hu/ $\sim$ jofri/JOFRI/OKTAT/pmmar.pdf

[2]	http://wikipedia.org/wiki/Richard_E._Bellmann

[3]	http://wikipedia.org/wiki/Bellmann_equation

¹p, mint partikuláris, azaz részleges

²A téma nagyon érdekes feldolgozása olvasható Énekes Béla ‐ Kós Géza: Néhány érdekesség a Fibonacci- és a Fibonacci-típusú sorozatokról I.‐II. (KöMaL, 2000/12. és 2001/1.) cikkekben.

³Richard E. Bellmann (1920‐1986), a dinamikus programozás atyja