Cím: A körsorokra vonatkozó feladatok megoldásai I.
Füzet: 1950/május, 124 - 128. oldal  PDF  |  MathML 
Témakör(ök): Ábrázoló geometria

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Körsorokra vonatkozó feladatok.

 

1. Bizonyítsátok be, hogy ha egy P pont nincs rajta két egymást metsző kör hatványvonalán, akkor más lesz a hatványa az egyik és a másik körre nézve.
 

Megoldás: Ha a két kör metszi egymást, akkor legyen egyik metszéspontjuk A. Mivel P nincs rajta a két kör közös húrján, sem meghosszabbításán, így a PA egyenes metszi mindegyik kört még egyszer két különböző B és C pontban. Egyikük A-ba is eshet, ha PA érinti az egyik kört.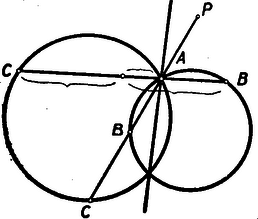
 
 

Ha P kívül van a BC közön, akkor PB≠PC és így PA⋅PB≠PA⋅PC. Ha P a B és C pont közt van, akkor lehet PB=PC, de akkor P elválasztja például a C pontot A-tól és B-től. Ekkor P az A-n és B-n átmenő körön kívül van, az A-n és C-n átmenőnek viszont a belsejében. Egy belső és egy külső pont hatványára viszont soha sem szoktuk azt mondani, hogy egyenlők. Megkülönböztetésül a belső pont hatványát szokás negatív előjelűnek is venni, annak jelzésére, hogy itt két P-ből ellenkező irányba induló távolság szorzatáról van szó, míg külső pont hatványát a ponttól egyirányba haladó távolságok szorzata adja.
E megoldás kapcsán felvetődik a következő kérdés: Mi a mértani helye azoknak a pontoknak, melyeknek két metsző körre vonatkozó hatványa ellenkező előjellel egyenlő?
 

2. Bizonyítsátok be, hogy az A és B pontokon át írható körsort derékszögben metsző k kör az A, B pontokhoz tartozó egyik Apollonius-kör.
 

Megoldás: Tudjuk, hogy az A és B pontokon átmenő körsort derékszögben metsző kör középpontja rajta van a körsor AB hatványvonalán, és megfordítva, ha egy kör, amelynek középpontja az AB egyenesen van a körsor egy körét derékszögben metszi, akkor derékszögben metszi az egész körsort. Így elég azt bizonyítanunk, hogy olyan kör, melynek középpontja az AB egyenesen van, és az AB mint átmérő fölé írt kört (a körsor legkisebb körét) derékszögben metszi, az az A és B pontokhoz tartozó egyik Apollonius-kör. Legyen az A és B ponton átmenő kör középpontja O, és a rá merőleges k köré O1, ennek metszéspontja a két kör centrálisával C és D, a két kör egyik metszéspontja pedig 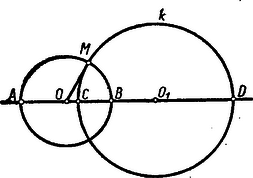M.
 
 

A k kört érinti az OM egyenes, így
OM2=OC⋅OD,OM=AO,
tehát
AO2=OC⋅OD,
vagy másképp írva:
AOOC=ODAO.
Ebből kapjuk, hogy
AO+OCAO-OC=OD+AOOD-AO
és minthogy AO=OB
AO+OCOB-OC=OD+AOOD-OB,
vagy
ACBC=ADBD.
Tehát valóban a k kör az A, B pontokhoz és a λ=ACBC arányhoz tartozó Apollonius-kör.
 

3. Jelöljük k-val az A és B pontokon átmenő körsor köreit, az erre ortogonális körsor köreit h-val. Bizonyítsuk be, hogy ‐ az A és B pont kivételével ‐ a síknak minden pontján egy és csakis egy k is h kör megy át.
 

Megoldás: a) A és B pontokon átmenő körsornak egy tetszőleges P ponton valóban csak egy köre megy át, ugyanis három pont (ha nem fekszik egy egyenesen) egyértelműen meghatároz egy kört. Ha A, B és P egy egyenesen vannak, akkor a hatványvonalat kapjuk, amelyet szintén a körsorhoz tartozónak tekintünk.
b) Mivel az A és B ponton átmenő körsort ortogonálisan metsző körsor elemei az A és B pontokhoz tartozó Apollonius-körök, azért csak azt kell bizonyítani, hogy egy P ponton egy és csakis egy, az A és B pontokhoz tartozó Apollonius-kör megy át. Ez pedig nyilvánvaló, mert APBP egyértelműen meghatározza az A, B és P pontokhoz tartozó Apollonius-kört. Ha PAB középmerőlegesén van, akkor a körsor keresett eleme ez a középmerőleges, azaz a körsor hatványvonala lesz, amit szintén a körsorhoz számítunk.
 

4. Legyen 1, 2, 3, 4, 5, 6 hat pont jele. Az 12, 34 és 56 találkozzék egy pontban. Ha 1234 és 3456 pontok egy-egy húrnégyszög csúcsai, bizonyítsátok be, hogy 5612 is húrnégyszöget tűz ki.
 

I. Megoldás: Célszerűbb lesz az adott pontokat A1, A2, A3, A4, A5, A6-tal jelölni. Legyen A1A2, A3A4 és A5A6 metszéspontja A7. Fektessünk az A1A2A3A4 illetőleg A3A4A5A6 pontokon k1 ill. k2 köröket. Rajzoljuk meg az A1A2A5 pontokon átmenő k3 kört. k1k2, és k3 hatványpontja nyilván A7 lesz. De A7 lesz a hatványpontja a k1k2 és az A1A2A6 pontokon átmenő k'3 köröknek is, tehát k3 és k'3 összeesik, vagyis A1A2A5A6, pontok egy körön vannak. Ha a hat pont nincs egy síkban, akkor a k1 és k2 körök sem lehetnek egy síkban. Két közös ponttal rendelkező, nem egy síkban fekvő két kör pedig mindig meghatároz egy és csakis egy gömböt. Ezen van tehát a k3 kör is.
 

II. Megoldás: Használjuk az előbbi jelöléseket. Ekkor A7A1⋅A7A2=A7A3⋅A7A4 és A7A3⋅A7A4=A7A5⋅A7A6 tehát A7A1⋅A7A2=A7A5⋅A7A6, vagyis az A1A2A5A6 négyszög húrnégyszög. Ha térben van a hat pont, akkor, mivel A7A1⋅A7A2=A7A3⋅A7A4=A7A5⋅A7A6, a hat pont köré gömb írható.
 

5. Adva van egy k kör és A, B pontok. Szerkesztendő az A, B pontokon átmenő kör, mely a k kört érinti.
 

Megoldás: Legyen a keresett kör ké. Két érintkező kör hatványvonala az érintkezési pontjukban húzott érintőjük. Ezt fogjuk először megszerkeszteni. Egy pontját három kör hatványpontja segítségével kaphatjuk meg.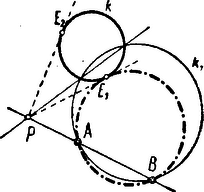
 
 

Bár a ké, kört még nem ismerjük, tudunk olyan k1 segédköröket rajzolni, hogy ismerjük k1 és ké hatványvonalát: bármely A-n és B-n átmenő kört véve az AB egyenes lesz ez a hatványvonal. Ha az egyszerűség kedvéért olyan k1 kört veszünk, mely k-t is metszi, C-ben és D-ben, akkor k és k1 hatványvonala a C-n és D-n átmenő egyenes. A két egyenes P metszéspontján kell átmennie tehát k és ké hatványvonalának is. Mivel k és ké érintkező körök, a P pontból a k körhöz húzott érintők felelnek meg a keresett hatványvonalul. Ezek E1 ill. E2 érintési pontja az A és B pontokkal meghatároz egy-egy kört, csak ezek lehetnek a keresett érintő körök.
Meg kell mutatnunk, hogy ezek valóban érintik a k kört. Ezt az A-n, B-n és E1-en átmenő körről fogjuk megmutatni. Elég azt megmutatni, hogy ez a kör érinti az E1 pontban a PE1 egyenest. Ez az egyenes hatványvonala a két körnek, mert a P pontot úgy szerkesztettük, hogy egyenlő legyen a hatványa a k körre és az A-n és B-n átmenő körökre nézve, E1-nek viszont mindkét körre vonatkozó hatványa 0. Ha a szerkesztett kör még egy pontban metszené a PE1, egyenest, akkor ennek a pontnak a rá vonatkozó hatványa 0 volna, a k körre vonatkozó hatványa viszont nem 0, mert a PE1 egyenes az E1 pontban érinti a k kört. Ez lehetetlen, tehát a szerkesztett körnek is érintenie kell az E1 pontban a PE1 egyenest, tehát érinti a k kört is.
 

6. Adva van k kör és A, B pontok. Szerkesztendő az A, B pontokon átmenő kör, mely a k kört derékszögben metszi.
 

Megoldás: Legyen az adott k kör középpontja O, sugara r. OB-nek a keresett körrel való másik metszése legyen C, akkor OC⋅OB=r2. Ebből OC megszerkeszthető. Az A, B és C pontok meghatározzák a keresett kört.
 

7. Tekintsük egy megadott háromszög oldalait, mint egy-egy kör átmérőjét. A hozzájuk tartozó három kör hatványpontja milyen összefüggésben van a háromszöggel?
 

Megoldás: Legyen az adott háromszög ABCΔ, a BC, CA, illetőleg AB fölé, mint átmérő fölé írt körök k1, k2 illetőleg k3. k1 és k2 másik közös pontja P. Nézzük meg először pl., hogy a k1 és k2 körök hatványvonala, a CP egyenes milyen összefüggésben van a háromszöggel. Thales tétele szerint CP⊥AP és CP⊥BP. Ez csak úgy lehetséges, ha P az AB oldalon van és CP⊥AB. Így k1 és k2 hatványvonala az ABCΔAC oldalhoz tartozó magassága. Ugyanúgy a másik két hatványvonal is a háromszög egy-egy magassága, tehát a három kör hatványpontja a háromszög magassági pontja.