Cím:	Matematikai olimpiász Moszkvában
Füzet:	1950/május, 142 - 154. oldal	PDF  |  MathML
Témakör(ök):	Ábrázoló geometria

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Matematikai olimpiász Moszkvában.   Az első forduló feladatainak megoldása: VII‐ VIII. osztályos csoport:   l. Bizonyítandó, hogy $\begin{array}{c}{\displaystyle {27195}^8-{10887}^8+{10152}^8}\end{array}$ osztható 26460-nal.   Megoldás: Jelöljük a kérdéses számot $N$-nel. ${27195}^8-{10887}^8$ osztható $27195-10887=16308=2^2\cdot 3^3\cdot 151$-gyel. Másrészt $10152=2^3\cdot 3^3\cdot 47$. Így mindkét tag, tehát $N$ is osztható $2^2\cdot 3^3=108$-cal. Másrészt $N$-et ${27195}^8-\left({10887}^8-{10152}^8\right)$ alakban írva a zárójelben álló különbség osztható $10887-10152=735$-tel és $27195=37\cdot 735$, tehát $N$ osztható $735$-tel is. $N$ osztható $2^2\cdot 3^3$-nal és $3\cdot 5\cdot 7^2$-nel is, tehát mindenesetre osztható az e1őforduló törzsszámok legnagyobb előforduló hatványaival, s így ezek szorzatával is: $2^2\cdot 3^3\cdot 5\cdot 7^2=26460$-nal is. Megjegyzés. A megoldásban annyit használtunk, hogy $a^n-b^n$ osztható $a-b$-vel. A 8-as kitevőre azonban többet is tudunk mondani: $\begin{array}{c}{\displaystyle a^8-b^8=\left(a^4+b^4\right)\left(a^4-b^4\right)=\left(a^4+b^4\right)\left(a^2+b^2\right)\left(a^2-b^2\right)=\left(a^4+b^4\right)\left(a^2+b^2\right)\left(a+b\right)\left(a-b\right)\mathrm{.}}\end{array}$ Ebből a szám nagyobb osztóját is ki tudjuk olvasni: $\begin{array}{c}{\displaystyle N=\left({27195}^4+{10887}^4\right)\left({27195}^2+{10887}^2\right)\left(27195+10887\right)\left(27195-10887\right)+2^{24}\cdot 3^{24}\cdot {47}^8\mathrm{.}}\end{array}$ Itt az első kifejezés első három tényezője páros, de $4$-gyel nem osztható az utolsó osztható 4-gyel, a szorzat tehát osztható $2^5$-nel is. $27195$ is, $10887$ is osztható 3-mal, így az első tényező $3^4$-nel, a második $3^2$-nel, a harmadik $3$-mal osztható, az utolsó tényező $3^3$-nal, a szorzat tehát $3^{10}$-nel is. Így $N=2^5\cdot 3^{10}A+2^{2}4\cdot 3^{2}4\cdot {47}^8$, ahol $A$ egész szám. $N$ tehát osztható $2^5\cdot 3^{10}$-nel. A második felbontásból ezúton sem nyerünk újabb olyan tényezőt, mely az előbbinek ne volna osztója, csak $5\cdot 7^2$-t. Így tehát azt kaptuk, hogy $N$ osztható $2^5\cdot 3^{10}\cdot 5\cdot 7^2=462944160$-nal is.   2. Bizonyítsuk be, hogy ha egy sokszögnek több szimmetriatengelye van, azok mind egy ponton mennek keresztül.   I. megoldás: Egy sokszög szimmetriatengelyei csak csúcsban vagy oldalközépponton metszhetik a kerületet. Így egy sokszögnek csak véges számú szimmetriatengelye lehet. Ha ezek nem mind egy ponton mennének keresztül, akkor volna köztük három, amelyik háromszöget alkot, vagy melyek közül kettő párhuzamos. 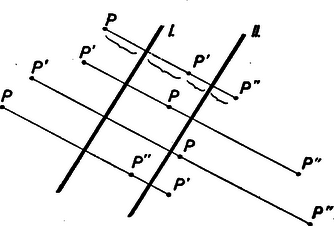    Ha $I$ és $II$ két különböző, de párhuzamos tengely és egy $P$ pont tükörképe $I$-re, $P\text{'}$, $P\text{'}$-é $I$-re $P8221;$, akkor ez a három pont egy egyenesbe esik és könnyű látni, hogy bárhova esik is a $P$ pont, a $PP"$ távolság mindig a két tengely távolságának kétszerese. Így két párhuzamos tengelyre való tükrözés mindig párhuzamos eltolást eredményez. De egy sokszöget szimmetriatengelyére tükrözve az önmagába megy át. Így a két egymásutáni tükrözés, tehát egy eltolás után is vissza kellene kerülnie eredeti helyére. Olyan sokszög viszont nincs, amely eltolás után eredeti helyére kerülne vissza, így egy sokszögnek nem lehetnek párhuzamos szimmetriatengelyei. Legyen $a\mathrm{,}b\mathrm{,}c$ három szimmetriatengely, melyek háromszöget alkotnak. A $b$ és $c$, $c$ és $a$, $a$ és $b$ metszéspontját jelöljük rendre $A\mathrm{,}B\mathrm{,}C$-vel. Az ezeknél a csúcsoknál fekvő szögeket rendre $\alpha \mathrm{,}\beta \mathrm{,}\gamma$-val. Feltehetjük, hogy $A$-n, $B$-n és $C$-n át nem indul szimmetriatengely a háromszög belsejébe, mert ha indulna pl. $A$-ból, akkor vehetnénk $c$ helyett azt a tengelyt, mely $b$-vel a legkisebb szöget zárja be. Ezt sorra a többi csúcsokra is folytatva egyszer el kell érnünk egy kívánt tulajdonságú háromszöghöz, mert összesen csak véges számban léteznek szimmetriatengelyek. Mivel szimmetriatengelyre tükrözve a sokszöget az önmagába megy át, kell, hogy ilyen tükrözésnél a szimmetriatengelyek is szimmetriatengelyekre kerüljenek. Tükrözzük pl. $b$-t $c$-re, aztán $c$-t $b$ tükörképére stb. Kell, hogy mielőtt az $A$-ból kiinduló féltengelyek $b$-nek $B$ csúccsal ellenkező oldalára kerülnének, az egyik tengely épp $b$-re essék, mert két szomszédos tengely szöge mindig $\alpha$, így ha $b$ az ismételt tükrözéssel talált tengelyek ketteje közé esnék, akkor a két tengely egyike viszont $A$-n keresztül a háromszög belsejébe jutna. Ez azt jelenti, hogy $\alpha$ valamely többszöröse éppen ${180}^{\circ }$. $k\alpha ={180}^{\circ }$, ahol $k$ egész szám. Hasonlóan kell olyan $l$ és $m$ egész számoknak is lenniük. hogy $l\beta ={180}^{\circ }$ és $m\gamma ={180}^{\circ }$ legyen. Innen $\begin{array}{c}{\displaystyle \alpha +\beta +\gamma =\frac{{180}^{\circ }}{k}+\frac{{180}^{\circ }}{l}+\frac{{180}^{\circ }}{m}={180}^{\circ }\mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle \frac{1}{k}+\frac{1}{l}+\frac{1}{m}=1.}\end{array}$ $lm$-mel átszorozva és rendezve: $\begin{array}{c}{\displaystyle \frac{lm}{k}=lm-l-m\mathrm{,}}\end{array}$ tehát $l\cdot m$ osztható $k$-val. Feltehetjük, hogy $k$-nak van $l$-lel egynél nagyobb közös osztója, $d$, azaz $k=d\cdot k\text{'}$, $l=d\cdot l\text{'}$. Innen $d\cdot k\text{'}\alpha ={180}^{\circ }=d\cdot l\beta$, vagyis $\begin{array}{c}{\displaystyle k\text{'}\alpha =l\text{'}\beta <{180}^{\circ }\mathrm{.}}\end{array}$ Az előző meggondolás szerint minden $A$-n átmenő egyenes szimmetriatengely, ha $AC$-vel bezárt szöge $\alpha$-nak egész számú többszöröse és hasonlóan minden olyan $B$-n átmenő egyenes is, melynek $AB$-vel bezárt szöge $\beta$-nak többszöröse. Így szimmetriatengelye a sokszögnek az az $A$-n átmenő egyenes is, mely $AB$-vel $k\text{'}\alpha$ szöget zár be és az a $B$-n átmenő egyenes is, mely $AB$-vel annak ellenkező oldalán $l\text{'}\beta$ nagyságú szöget zár be. Ezek azonban a sokszög különböző párhuzamos szimmetriatengelyei volnának, de láttuk, hogy ez lehetetlen. Egy sokszögnek tehát háromszöget alkotó szimmetriatengelyei sem lehetnek.   II. megoldás: Az előbbi bizonyításban a sokszögek tulajdonságaiból annyit használtunk csak ki, hogy csak véges számú szimmetriatengelyük lehet, ezt is csak akkor, mikor azt bizonyítottuk, hogy háromszöget alkotó szimmetriatengelyek nem lehetnek. Most megmutatjuk, hogy még ez a feltétel sem szükséges, ha alaposabban megvizsgáljuk a tükrözések tulajdonságait. Vizsgáljuk először, hogy hova jut egy tetszőleges pont, ha $a$-ra, majd $b$-re tükrözzük. Legyen ismét egy tetszőleges $P$ pont tükörképe $a$-ra $P\text{'}$, $P\text{'}$-é $b$-re $P8221;$, továbbá $PCa\sphericalangle =\phi$, $P\text{'}Cb\sphericalangle =\psi$. Ekkor $CP=CP\text{'}=CP8221;$. Jelöljük az $a$ és $b$ egyenes szögét $\gam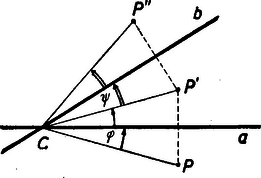ma$-val.     Ekkor könnyű látni, hogy $PCP"\sphericalangle =2\phi +2\psi$, ha az olyan szöget negatívnak vesszük, melynek az először említett szárát ellenkező irányban kell a másodszor nevezett szárra fordítani, mint amilyen irányban az $a$ tengelyt $\gamma$-nyi elfordítással a $b$ tengelyre fordíthatjuk. Ilyen előjel meghatározás melleit viszont $\phi +\psi =\gamma$, tehát $PCP"\sphericalangle =2\gamma$, bármely pont is a síkban $P$. Két egymást metsző tengelyre való tükrözés tehát mindig a sík elfordítását eredményezi a tengelyek metszéspontja körül az első tengelytől a második felé mutató irányban a tengelyek szögének kétszeresével. Ha most $a\mathrm{,}b\mathrm{,}c$ egy síkidom háromszöget alkotó szimmetriatengelyei, akkor pl. $c$-re tükrözve sajátmagába kell átmennie az idomnak, tehát szimmetriatengelyei is szimmetriatengellyel cserélődnek fel. $a$-nak és $b$-nek $c$-re vonatkozó $a\text{'}$ és $b\text{'}$ tükörképe is szimmetriatengelye tehát az idomnak. Eszerint önmagába megy át az idom akkor is, ha egymásután tükrözzük az $a\mathrm{,}b\mathrm{,}a\text{'}\mathrm{,}b\text{'}$ egyenesekre. 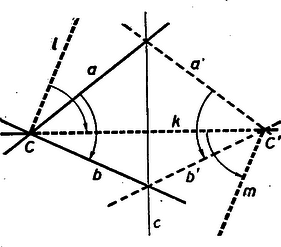    Az első két tükrözés azt eredményezi, hogy elforgatjuk idomunkat az $a$ és $b$ tengelyek $C$ metszéspontja körül $2\left(a\mathrm{,}b\right)\sphericalangle =2\gamma$-val, a második két tükrözés együtt pedig az $a\text{'}$ és $b\text{'}$ tengelyek $C\text{'}$ metszéspontja körül $2\left(a\text{'}\mathrm{,}b\text{'}\right)\sphericalangle =-2\left(a\mathrm{,}b\right)\sphericalangle =-2\gamma$-val való forgatáshoz vezet (vagyis ellenkező irányú elforduláshoz ugyanakkora szöggel.) Ezek tehát önmagába viszik át a sokszöget. Ugyanezeket az elfordulásokat eredményezi azonban nem csak ez a négy tükrözés, hanem bármelyik négy, amelyik először két $C$-n átmenő és $\gamma$ nagyságú szöget bezáró tengelyre, majd két $C\text{'}$-n átmenő és $-\gamma$ szöget bezáró tengelyekre történik. Ha az egymásután elvégzett négy tükrözés hatásáról akarunk képet alkotni magunknak, akkor célszerű lesz nem találomra választott négy tengelyt használni, hanem alkalmasan kiválasztottakat. Célszerű lesz felhasználni a $CC\text{'}$ egyenest ‐ jelöljük $k$-val, ‐ mert ezt használhatjuk úgy is, mint $C$-n átmenő és úgy is, mint $C\text{'}$-n átmenő tengelyt. Elég tehát még egy tengelyt választani C-n át úgy, hogy $\left(l\mathrm{,}k\right)\sphericalangle =\gamma$ legyen és egy $m$ tengelyt $C\text{'}$-n át úgy, hogy $\left(k\mathrm{,}m\right)\sphericalangle =-\gamma$ legyen. $l$ és $m$ ekkor párhuzamos. Ezek az egyenesek nem kell, hogy szimmetriatengelyei legyenek az adott idomnak, tehát egyre-egyre végezve tükrözést általában nem megy át az idom önmagába; ha azonban egymásután tükrözzük az $l$ és $k$ egyenesre, akkor tulajdonképpen elforgatunk a $C$ pont körül $2\left(l\mathrm{,}k\right)\sphericalangle =2\gamma$ szöggel, azt pedig tudjuk, hogy ez az elmozdítás már önmagába viszi át az idomot. Tükrözzük ezután még egyszer a $k$, majd az $m$ egyenesre, ez $C\text{'}$ körül $2\left(k\mathrm{,}m\right)\sphericalangle =-2\gamma$ szöggel való forgatást jelent, tehát ismét önmagába viszi át az idomot. A négy tükrözés egymásutáni elvégzése tehát önmagába viszi át a sokszöget. E közben a $k$ tengelyre kétszer egymásután tükröztünk. Ezen két tükrözés után azonban minden pont visszakerül a tükrözés előtti helyére. Így a négy tükrözés után ugyanoda jut minden pont, mintha csak az $l$ és aztán mindjárt az $m$ egyenesre tükröztük volna őket. Ez a két tükrözés is önmagába kell, hogy átvigye az idomokat. Ez azonban nem lehetséges, mert $l$ és $m$ párhuzamos tengelyek és láttuk, hogy egymásután két párhuzamos tengelyre tükrözve egy idomot az eredmény egy eltolással helyettesíthető a tengelyekre merőleges irányban. Ezzel kimutattuk, hogy nem lehet a sokszögnek három szimmetriatengelye, mely háromszöget alkot. Megjegyzések. A bizonyítás utolsó részében azt a magában érdekes tételt bizonyítottuk be, hogy ha egymásután végezünk a síkban forgatást két különböző pont körül egyenlő szöggel, de ellenkező irányban, akkor ez a mozgás helyettesíthető egy eltolással. A bizonyítás sehol sem használta ki, hogy sokszög az idom, amelyről beszélünk tehát a tétel igaz minden olyan idomra, mely nem nyúlik a végtelenbe. Ha egy párhuzamos szélű papírcsíkot mindkét irányban vég nélkül meghosszabbítva képzelünk, annak már szimmetriatengelye lesz minden a széleire merőleges egyenes, tehát párhuzamos egyenesek (ezen kívül még a középvonala is). A 3. feladat megoldását a IX‐X. osztályos csoport első feladatával együtt tárgyaljuk.   4. Bizonyítsuk be, hogy ha egy síkbeli zárt törtvonal hosszúsága 1, akkor a törtvonal lefedhető egy 1/4 sugarú körrel.   Megoldás: Jelöljünk ki a törtvonalon két $A$ és $B$ pontot úgy, hogy a törtvonal hosszát felezzék. A két pontot összekötő húr hossza a feltétel szerint legfeljebb 1/2 lehet. Rajzoljuk meg azt az 1/4 sugarú kört, melynek középpontja az $AB$ egyenes $O$ felezőpontjában van. Azt akarjuk bizonyítani, hogy a törtvonal tetszésszerinti pontja ezen a körön belül van. Kössük össze a kerületnek egy $P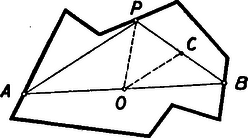$ pontját $O$-val, $A$-val és $B$-vel.     A $PA$ és $PB$ távolságok összege kisebb az $A$-tól $P$-n át $B$-ig haladó törtvonal hosszánál, ami éppen 1/2. Jelölje $C$ a $PB$ távolság felezőpontját; nyilván $OC$ az $AP$ távolság fele. Az $OP$ távolságra az $OPC▵$-ból: $\begin{array}{c}{\displaystyle OP<OC+CP=\frac{1}{2}\left(AP+BP\right)\leqq \frac{1}{4}\mathrm{,}}\end{array}$ amint állítottuk. Megjegyzés. A bizonyításban sehol sem használtuk ki azt, hogy törtvonalról van szó. gy a fenti bizonyításból az is következik, hogy ha egy zárt vonal hossza l, akkor az mindig lefedhető egy 1/4 sugarú körrel.   5. Bizonyítsuk be, hogy egy tetszőleges háromszögben a beírt kör középpontját és valamelyik, a háromszöghöz hozzáírt kör középpontját összekötő egyenesszakaszt a háromszög köré íri kör felezi.   Megoldás: Legyen $ABC▵$ egy háromszög, $qalpha\mathrm{,}\beta \mathrm{,}\gamma$ a szögei, $O$ a beírt kör középpontja, $O_a$ a $BC$ oldalhoz hozzáírté. Messe az $O{O}_a$ egyenesszakasz a körülírt kört $D$-ben.     $A{O}_a\mathrm{,}BO$ és $B{O}_a$ felezi rendre $\alpha$-t, $\beta$-t, illetve a háromszög $B$-nél fekvő külső szögét, tehát $\begin{array}{c}{\displaystyle CB{O}_a\sphericalangle =\frac{\alpha +\beta }{2}\mathrm{,}}\end{array}$ $\begin{array}{c}{\displaystyle CBD\sphericalangle =CAD\sphericalangle =\frac{\alpha }{2}\mathrm{.}}\end{array}$ Így $\begin{array}{c}{\displaystyle OBD\sphericalangle =\frac{\alpha +\beta }{2}\text{ és }DB{O}_a\sphericalangle =\frac{\gamma }{2}\mathrm{.}}\end{array}$ Mint az $AOB▵$ külső szöge, $\begin{array}{c}{\displaystyle BO{O}_a\sphericalangle =OAB\sphericalangle +OBA\sphericalangle =\frac{\alpha +\beta }{2}\mathrm{.}}\end{array}$ Végül a $BD{O}_a▵$ külső szöge $ADB\sphericalangle =ACB\sphericalangle =\gamma$ s így $D{O}_{a}B\sphericalangle =ADB\sphericalangle -DB{O}_a\sphericalangle =\frac{\gamma }{2}$. Így $ODB▵$ és $BD{O}_a▵$ egyenlőszárú, tehát $\begin{array}{c}{\displaystyle OD=BD=D{O}_a\mathrm{.}}\end{array}$   IX ‐ X. osztályos csoport. VII ‐ VIII. osztályos csoport 3. Bizonyítsuk be, hogy az $x^2+y^2+z^2=2xyz$ egyenletnek nincs más egész értékű megoldása, mint $x=y=z=0$. IX ‐ X. osztályos csoport 1. Keressünk olyan $x\mathrm{,}y\mathrm{,}z$ és $v$ egész számokat, melyekre teljesül, hogy $x^2+y^2+z^2+v^2=2xyzv$.   Megoldás: 3. Válasszuk külön mindegyik változó törzstényez6s felbontásából 2 hatványát: legyen $x=2^{a}p\mathrm{,}y=2^{b}q\mathrm{,}z=2^{c}r$, ahol $p\mathrm{,}q\mathrm{,}r$ páratlan számok. Mivel a változók szerepe az egyenletben teljesen szimmetrikus, feltehetjük, hogy olyan sorrendben következnek, hogy $a\leqq b\leqq c$. Az egyenlet így írható: $\begin{array}{c}{\displaystyle 2^{2a}\cdot p^2+2^{2b}\cdot q^2+2^{2c}\cdot r^2=2^{1+a+b+c}\cdot pqr\mathrm{,}}\end{array}$ és mindkét oldalt elosztva $2^{2a}$-val, $\begin{array}{c}{\displaystyle p^2+2^{2\left(b-a\right)}\cdot q^2+2^{2\left(c-a\right)}\cdot r^2=2^{b-a+c+1}\cdot pqr\mathrm{.}}\end{array}$ Ha $b>a$, a jobboldal páros. A baloldal csak akkor lehet páros, ha $p=0$, de ekkor a jobboldal is 0 lévén, $y^2+z^2=0$, vagyis $x=y=z=0$. Ha $b=a$, a jobboldal, akkor is páros, a baloldalon az első két tag $p^2+q^2$ páros összeget ad, de 4-gyel nem osztható, mert páratlan szám négyzete mindig 1-gyel nagyobb, egy 4-gyel (sót, 8-cal) osztható számnál. Így kell, hogy $c>a$ legyen, tehát $c$ legalább l. Egyenletünk így írható: $\begin{array}{c}{\displaystyle p^2+q^2=2^{c+1}pqr-2^{2\left(c-a\right)}{r}^2\mathrm{.}}\end{array}$ Így a jobboldal 4-gyel osztható, a bal azonban nem, tehát ismét nem kapunk 0-tól különböző megoldásokat.   1. Az előbbihez hasonlóan feltehetjük, hogy $x=2^a\cdot p\mathrm{,}y=2^b\cdot q\mathrm{,}z=2^c\cdot r$ és $v=2^d\cdot s$, ahol $a\leqq b\leqq c\leqq d$. és $p\mathrm{,}q\mathrm{,}r\mathrm{,}s$ páratlan számok. $2^{2a}$-nal osztva: $\begin{array}{c}{\displaystyle p^2+2^{2\left(b-a\right)}{q}^2+2^{2\left(c-a\right)}{r}^2+2^{2\left(d-a\right)}{s}^2=2b-a+c+d+1pqrs\mathrm{.}}\end{array}$ Ha $b>a$, vagy $b=c=a$, $d>a$, akkor a baloldal páratlan volna, a jobb páros. Legyen $b=a$, tehát $\begin{array}{c}{\displaystyle p^2+q^2+2^{2\left(c-a\right)}{r}^2+2^{2\left(d-a\right)}{s}^2=2^{c+d+1}pqrs\mathrm{.}}\end{array}$ Ha $c>a$, akkor a baloldal csak 2-vel osztható, a jobb 4-gyel is. Ha viszont $c=d=a$, akkor a baloldal osztható 4-gyel, de 8-cal nem. A jobb csak 2-vel, ha $c$ és $d$ értéke 0, viszont ha $c=d\geqq 1$, akkor meg 8-cal is osztható a jobboldal. Ekkor sem szolgáltat az egyenlet 0-tól különböző megoldásokat.   2. Hogy helyezkednek el a szimmetriasíkjai annak a testnek, melynek két forgástengelye van?   Megoldás: A feltételekből következik, hogy véve egy forgástengelyt és a test egy ezen kívül eső pontját, a ponton át a tengely körül rajzolható a tengelyre merőleges síkú kör is a testhez tartozik. Először megmutatjuk, hogy a test két forgástengelye metszi egymást. Valóban ha volna két párhuzamos forgástengelye, akkor messük át ezekre merőlegesen valahol a testet. A keresztmetszet határvonala kör kell, hogy legyen, melynek a középpontja a tengely döféspontja a síkon. De ez esetünkben egy olyan körhöz kellene, hogy vezessen, melynek két különböző középpontja van, ami lehetetlen, tehát párhuzamos forgástengelyek sem lehetnek. Ha, két kitérő forgástengely volna, akkor keressük meg az elsőre merőleges keresztmetszetek közül azt (vagy egy olyant) melynek legnagyobb a külső körvonala (mely most is kör). 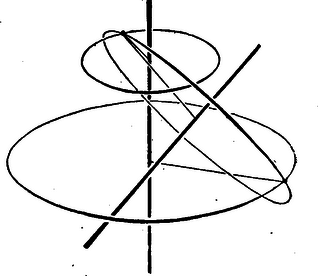    Vegyük ennek a körnek egy olyan pontját, mely a második tengelytől messzebb esik, mint a kör sugara. (Ilyen van. Vezessünk pl. a kör középpontján át a második tengelyre merőleges síkot. Ez két pontban metszi a kört. Ezek közül legalább az egyik messzebb van a második tengelytől, mint az első körüli kör sugara.) A testhez kell tartoznia annak a körnek is, mely átmegy ezen a ponton, síkja merőleges a második tengelyre és középpontja a második tengelyen fekszik. Az előbbi meggondolás szerint van e körnek olyan pontja, mely az első tengelytől esik messzebb, mint e kör sugara, tehát még inkább messzebb, mint az első tengely körül rajzolt kör sugara. Ez azonban azt jelentené, hogy volna a testnek az első tengelyre merőleges nagyobb sugarú keresztmetszete is, mint az először kiválasztott, de ez lehetetlen. Egy testnek tehát két kitérő forgástengelye sem lehet. A két forgástengely tehát metszi egymást. Legyen metszéspontjuk $O$. Mivel a test egyik forgástengelye körül bármekkora szöggel elforgatva önmagába megy át, kell, hogy a második forgástengely is mindig forgástengelybe menjen át. Így azon kúpfelület minden alkotója szimmetriatengely, melyet pl. az első tengely körül forgatva a második tengely leír. Ennek csúcsa $O$, nyílása a két tengely szögének kétszerese. Ezen kúp egy alkotója mentén továbbforgatva a testet a tengelyek most fel fogják ölelni egy olyan $O$-csúcsú kúp minden felszíni és belső egyenesét is, mely $O$-n megy át és melynek nyílása az előbbi kúp nyílószögének a kétszerese. Ismét egy alkotó körül forgatva olyan kúpot nyerünk, melynek összes egyenese szintén forgástengely és nyílásszöge kétszer akkora, mint az előbbié. Így véges számú lépés után azt kapjuk, hogy minden $O$-n átmenő egyenes forgástengelye a testnek. Ekkor a test határfelületei csak $O$ középpontú gömbök lehetnek. Így minden $O$-n átmenő sík szimmetriasík.   3. Keressük a következő egyenlet való8 megoldásait: $\begin{array}{c}{\displaystyle x^2+2ax+\frac{1}{16}=-a+\sqrt[]{a^2+x-\frac{1}{16}}\left(0<a<\frac{1}{4}\right)}\end{array}$   I. megoldás: Mindkét oldalhoz $a^2$-et adva: $\begin{array}{c}{\displaystyle {\left(x+a\right)}^2+\frac{1}{16}=a^2-a+\sqrt[]{a^2+x-\frac{1}{16}}\mathrm{.}}\end{array}$ Kis átalakítással. mindkét oldal $u^2+u$ alakra hozható, csak $\frac{1}{16}$-ot, illetőleg $-a$-t kell az ellenkező oldalra vinni és mindkét oldalhoz hozzáadni $x$-et. Ha ehhez még 1/4-et adunk, $u^2+u+1/4={\left(u+1/2\right)}^2$ folytán mindkét oldalon teljes négyzetet kapunk és így a feladatot másodfokú egyenletek megoldására vezethetjük vissza: $\begin{array}{c}{\displaystyle {\left(x+a\right)}^2+\left(x+a\right)+\frac{1}{4}=a^2+x-\frac{1}{16}+\sqrt[]{a^2+x-\frac{1}{16}}+\frac{1}{4}\mathrm{,}}\end{array}$ $\begin{array}{c}{\displaystyle {\left(x+a+\frac{1}{2}\right)}^2={\left(\sqrt[]{a^2+x-\frac{1}{16}}+\frac{1}{2}\right)}^2}\end{array}$ , tehát $\begin{array}{c}{\displaystyle x+a+\frac{1}{2}=\sqrt[]{a^2+x-\frac{1}{16}}+\frac{1}{2}\mathrm{,}}\end{array}$ vagy $\begin{array}{c}{\displaystyle x+a+\frac{1}{2}=-\sqrt[]{a^2+x-\frac{1}{16}}-\frac{1}{2}\mathrm{,}}\end{array}$ az első egyenletből a négyzetgyök eltávolítása után az $x^2+\left(2a-1\right)x+\frac{1}{16}=0$ egyenletet kapjuk. Innen $\begin{array}{c}{\displaystyle x=\frac{1-2a}{2}\pm \sqrt[]{{\left(\frac{1-2a}{2}\right)}^2-{\left(\frac{1}{2}\right)}^2}=\frac{1-2a}{2}\pm \frac{\sqrt[]{\left(1-4a\right)\left(3-4a\right)}}{4}\mathrm{.}}\end{array}$ Ez valós, ha $4a\leqq 1$, és ha $4a\geqq 3$. A második egyenletnek nincs valós megoldása, ha $0<a<1/4$, mert ha volna, annak mindenesetre negatívnak kell lennie, s így $a^2+x-\frac{1}{16}<x$ negatív volna. A második egyenlet az $\begin{array}{c}{\displaystyle x^2+\left(2a+1\right)x+2a+\frac{17}{16}=0}\end{array}$ egyenletre vezet, melynek gyökei $\begin{array}{c}{\displaystyle x=-\frac{2a+1}{2}\pm \sqrt[]{{\left(\frac{2a-}{2}\right)}^2-\frac{17}{16}}\mathrm{.}}\end{array}$ Ezek akkor valósak, ha $\begin{array}{c}{\displaystyle 2a-1>\frac{\sqrt[]{17}}{2}\mathrm{,}a>\frac{\sqrt[]{17}+2}{2}\text{vagy ha}2a-1<-\frac{\sqrt[]{17}}{2}\mathrm{,}a<-\frac{\sqrt[]{17}-2}{2}\mathrm{.}}\end{array}$   II. megoldás: A jobboldali kifejezés hasonlít ahhoz, mely a baloldal $0$-helyét állítja e1ő, csak az $x$ fölösleges a gyökjel alatt. Ha e kifejezés értékét y-nal jelöljük: $-a+\sqrt[]{a^2+x-\frac{1}{16}}=y$, innen $y^2+2ay+\frac{1}{16}=x$. Akkor megoldása $x$ az eredeti egyenletnek, ha a jobboldal értéke is megegyezik $y$-nal. Így az $\begin{array}{c}{\displaystyle x^2+2ax+\frac{1}{16}=y}\end{array}$ $\begin{array}{c}{\displaystyle y^2+2ay+\frac{1}{16}=x}\end{array}$ egyenletrendszerhez jutunk. Különbségüket képezve: $\begin{array}{c}{\displaystyle x^2-y^2+2a\left(x-y\right)=y-x\mathrm{,}}\end{array}$ azaz: $\begin{array}{c}{\displaystyle \left(x-y\right)\left(x+y+2a+1\right)=\mathrm{0,}}\end{array}$ Innen $x-y=0$, vagy $x+y+2a+1=0$ és $y$ értékét az első egyenletből behelyettesítve az előző megoldásban tárgyalt két másodfokú egyenlethez jutunk.   4. Legyen $4n$ pozitív számunk, melyeknek az a tulajdonsága, hogy bármely 4 egymástól különbözőből geometriai haladványt alkothatunk. Bizonyítsuk be, hogy ezek között a számok között található $n$ egyenlő.   Megoldás: Azt fogjuk bizonyítani, hogy nem lehet a $4n$ szám közt 4-nél több különböző. Ha volna 5 különböző, akkor legyenek ezek növekvő sorrendben $a\mathrm{,}b\mathrm{,}c\mathrm{,}d\mathrm{,}e$. Negatív és pozitív számok nem szerepelhetnek köztük vegyesen, mert akkor valamelyik féle, pl. negatív tag legalább három fordul elő az öt szám közt. De ekkor kiválasztható közüliik 3 negatív és egy pozitív, azok pedig nem alkothatnak mértani haladványt. Ha mind egyező e1őjelű, tegyük fel, hogy mind pozitív. (Csupa negatív tagra ugyanígy okoskodhatunk.) Ekkor kellene, hogy $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ és $a\mathrm{,}b\mathrm{,}c\mathrm{,}e$ is mértani haladványt alkosson, mégpedig a tagok ilyen sorrendjében, mert egy pozitív tagú mértani sor mindig monoton (a szerint növ6 vagy fogyó; hogy melyik végéről nézzük.) Kell tehát, hogy $\begin{array}{c}{\displaystyle \frac{c}{b}=\frac{d}{c}\text{és}\frac{c}{b}=\frac{e}{c}\mathrm{.}}\end{array}$ legyen, amiből $d=e$ következik, ellentétben azzal a feltevéssel, hogy $a\mathrm{,}b\mathrm{,}c\mathrm{,}d\mathrm{,}e$ csupa különböző számok. Ha viszont $4n$ szám közt csak négy különböző érték fordulhat elő, akkor valamelyik értéknek legalább n-szer kell köztük előfordulnia.   5. Bizonyítsuk be, hogy ha egy hatszög szemközti oldalai párhuzamosak, és a szemközti csúcsokat összekötő átlók egyenők, akkor kör írható a hatszög köré.   Megoldás: Egy ilyen, a feltételeknek eleget tevő hatszögben bármely két szemközti oldal végpontjai olyan négyszöget tűznek ki, melynek átlói egyenlők, egyik oldalpárjuk pedig párhuzamos. Megmutatjuk, hogy az ilyen négyszög szimmetrikus trapéz. Tegyen $ABCD$ négyszög eleget a feltételeknek $\left(AB\parallel CD\mathrm{,}AC=BD\right)$. Húzzunk párhuzamost az A ponton át $BD$-vel, ennek $CD$-vel való metszéspontja legyen $E$. $AE$ és $BD$ párhuzamos lévén $AED\sphericalangle =BDC\sphericalangle$. Másrészt azonban $AE=BD=AC$, így $EAC$ háromszög egyenlőszárú, vagyis $AED\sphericalangle =ACD\sphericalangle$ és ebből $BDC\sphericalangle =ACD\sphericalangle$. És így a négyszög valóban szimmetrikus trapéz. 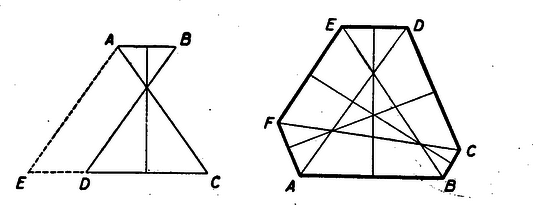    Legyen most $ABCDEF$ a feltételeknek megfelelő hatszög. Ekkor az előbbiek szerint $ABDE$, $BCEF$ és $CDFA$ szimmetrikus trapézek. Így a párhuzamos oldalak felező merőlegese az átlók metszéspontján megy át és felezi azok szögét. A három oldalpár felező merőlegeseit meghúzva az átlók alkotta háromszög szögfelezőit kapjuk. Ezekről tudjuk, hogy egy ponton (a háromszögbe írt kör középpontján) mennek át Ez a pont egyenlő messze van $A$-tól és $B$-tő1, $B$-tő1 és $C$-tő1, $C$-től és $D$-től, $D$-től és $E$-től, $E$-tő1 és $F$-tő1, végül $F$-től és $A$-tól, tehát középpontja egy olyan körnek, mely a hatszög minden csúcsán átmegy.   A verseny második fordulóján a következő tételek voltak kitűzve: VII ‐ VIII. osztályos csoport:   203. (1.) Egy kör mentén $12$ mező helyezkedik el. Ezek közül négy szomszédoson $4$ különböző figura: sorra egy vörös, egy sárga, egy zöld és egy kék. Minden figura úgy mozdítható el, hogy bármelyik irányban négy szomszédos mezőt átlépve az ötödikre helyezzük, feltéve, hogy ezen a mezőn még nem áll figura. Bizonyos számú lépés után a figurák visszakerültek arra a négy mezőre, amelyen eredetileg álltak, csak más sorrendben. Hányféle sorrendben kerülhetnek vissza eredeti helyükre?   204. (2) Legyen $ABC$ és $DEF$ két tetszőleges adott háromszög és $O$ egy adott pont a síkban. $X$ és $Y$ jelentse az $ABC\Delta$, illetve a $DEF\Delta$ egy-egy tetszőleges pontját. Keressük meg minden ilyen pontpárhoz azt a $Z$ pontot, melyre $OXZY$ egy paralelogramma. a) Bizonyítandó, hogy az összes ilyen $Z$ pontok egy sokszöget töltenek ki. b) Hány oldala lehet ennek a sokszögnek? c) Bizonyítandó, hogy a keletkező sokszög kerülete egyenlő a két háromszög kerületének összegével.   205. (3) $31$ súlyunk van, melyek mindegyike valamilyen egész számú grammot nyom. Azt tudjuk róluk, hogy bármelyik $12$ súly úgy választható két hatos csoportra, hogy azok súlya egyenlő legyen. Bizonyítandó, hogy a súlyok mind egyenlők.   206. (4) Egy tetszőleges hatszögben kössük össze minden oldal középpontját a következő második oldaléval. Két háromszöget kapunk. Bizonyítandó, hogy e két háromszögnek ugyanaz a súlypontja.   (5) $100$ egész szám van adva. Bizonyítandó, hogy kiválasztható valamennyi ezek közül (esetleg egy vagy mind) úgy, hogy azok összege osztható $100$-zal.   207. (6) Adva van a síkban egy kör és egy pont. $A$ pontból kiindulva egy olyan zárt törtvonalon haladunk végig, melynek minden szakasza a kör egy érintőjén fekszik, míg visszajutunk a kiindulási helyre. Azokat az útrészeket, melyeken közeledtünk számítsuk pozitív előjellel, azokat, melyeken távolodtunk, negatív előjellel. Bizonyítandó, hogy az ilyen előjelekkel vett útdarabok összege $0$.   IX ‐ X. osztályos csoport: Az 1. és 3. feladat megegyezik az előző csoport megfelelő számú feladataival.   208. (2) Rakjunk össze olyan egybevágó téglákból, melyek alakját az ábra mutatja, domború (beszögelés nélküli) testet. ($ABCD$ és $CDEF$ két egymásra merőleges négyzet. $ABG$ és $EFH$ ezekre merőlegesen álló egyenlőszárú derékszögű háromszög alakú lapok. A további lapokat a $GA$ és $AD$, $GB$ és $BC$, $DE$ és $EH$, végül $CF$ és $FH$ éleken átfektetett síkok alkotják, melyek közös $K$ pontban találkoznak.) 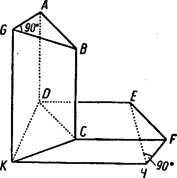    209. (4) Rajzoljunk adott háromszögbe olyan sokszöget, mely egy pontra szimmetrikus, és amelyiknek a lehető legnagyobb a területe.   (5) Bizonyítsuk be, hogy $2^n$ alakú számok alkalmas $n$ kitevő mellett tetszőlegesen előre megadott számjegysorozattal kezdődhetnek.   (6) Bizonyítandó, hogy egy négyzethez nem illeszthetünk hozzá $8$-nál több vele egybevágó négyzetet, hogy mindegyik hozzáérjen az adott négyzet kerületéhez, de se az adott négyzetbe, se egymásba ne nyúljanak.   Ezek közül az első csoport 5. feladata lényegében megegyezik a Bolyai Társulat által 1948-ban rendezett matematikai tanulóverseny első tételével. A második csoport 5. feladatának megoldása viszont a középiskolai anyagon túlmenő ismereteket követelne. Így e két feladat kivételével a többit tűzzük csak ki megoldásra.